分布式信息管理系统混合加密优化研究

陈永锋 ，宋 楠

（西安建筑科技大学管理学院，陕西 西安 710055）

随着信息技术的不断发展，信息管理系统为人们带来了很多便利．其中分布式系统更是将不同地点的系统连接起来，方便了管理也减少了投入．但是分布式信息管理系统面临大量的数据交互，其安全与效率问题一直无法兼顾．本文以多校区一卡通系统为例，提出混合加密算法从软件的角度提供一种解决思路．

保障信息安全的主要手段是进行数据加密，其由密钥种类可分为对称加密和非对称加密[1]．对称加密算法最具代表性的就是1977年公布实施的DES算法作为数据加密标准[2]，在这以后有 3DES算法[3]、Rijndael算法[4]、RC5 算法[5]、IDEA 算法[6]等．而非对称加密算法应用最广的是 RSA算法[6]，它的特点是易于实现，基于大素数分解安全性高，既能加密数据又能进行数字签名身份认证．其他非对称加密算法还有Elgamal算法、ECC算法(椭圆曲线算法)等．

RSA算法由于算法效率问题不能应用与大数据量加密[7]，各国学者也对其进行了大量的研究以提升运算效率．2003年Sung-Ming Yen提出牺牲存储空间以提升运算效率，瑞士科学家也解决了 768位RSA算法密钥问题[8]．我国学者也取得了大量成就，王晓云教授破解MD5[9]与SHA-1[10]算法震惊世界，冯登国院士与陈相宁教授分别提出了运用中国剩余定理[11]和蒙哥马利算法[12]提高运算效率．

目前国内高校一卡通系统基本都采取对称加密算法进行数据加密，其加解密速度快，安全性高，适用于大数据量的数据加密与传输．其中 3DES加密算法发展成熟，易于实现且与已有的DES加密应用兼容，保护已有的使用DES的软件和硬件投资．但是单纯的对称加密有其不足之处，校园一卡通系统的消费终端很多，分布很广．其安全性具有一定风险，对称加密无法识别消息来源．这种情况下易遭到第三方恶意篡改消息与伪造消息，同时密钥管理和密钥更换时的风险也很高．而数据签名认证消耗的时间很多，对大数据传输效率造成很大影响．

本文结合3DES算法与RSA算法以混合加密的方式解决系统数据加密面临的问题．

1 混合加密算法

1.1 两种加密算法的优劣

1) 从密钥管理方面看，3DES算法明显不如RSA算法．密钥的生命周期有限，为了保证数据安全必须不断更新密钥．因为3DES算法是对称加密算法，其密钥需要在通信前进行秘密分配，对于不同的通信对象分配不同的密钥，在密钥分配管理传递的过程中密钥泄露的风险高．所以其密钥更换困难，风险大，密钥管理难度高．而RSA算法公开分配加密密钥，对加密密钥的更新容易，对不同的通信对象，也只需保证自己的私钥安全即可．

2) 从加解密效率来看，3DES算法高过RSA算法很多．因为3DES算法大多数操作是字节的位移和替换，使用计算机编程可以较快速实现，适用于大量快速的加解密运算．而RSA算法是基于大整数分解困难的计算进行的，加解密过程中需要进行高阶模幂运算，非常耗时．因此，RSA算法在大量多次数据加密过程中并不适用．

3) 从身份认证和消息验证方面来看，因为3DES算法是对称加密算法，使用一个密钥所以无法进行数字签名．而RSA算法可以进行身份验证和数字签名，其签名过程也非常容易实现．

4) 安全性方面两个算法的安全性都比较高，目前没有成熟的攻击手段破解这两个算法．

1.2 混合加密算法

本文在分析了两种算法的优劣并对 RSA算法的加解密运算进行了部分优化的基础上，结合两种算法的优势，提出一种既能快速进行大量数据加密也能进行身份验证和消息完整度验证的混合加密体制．其运行过程如下：A发送方，RSA算法公钥PUA、私钥PRA，3DES算法密钥K; B接收方，RSA算法公钥PUB、私钥PRB．

如果没有进行密钥分配或者需要更换密钥，A使用PUB采用RSA算法加密K，得到SK；

1) 计算散列值h=H(M)作为标识，并用PRA加密h，得到签名S；

2) 使用K采用3DES算法加密明文M和S，得到需发送的消息D；

3) 若没有进行密钥分配或者需要更换密钥，A将SK和D发送给B；否则，A将D发送给B；

4) 如果接收到SK, B使用PRB采用RSA算法解密SK，得到K；5) 使用K采用3DES算法解密D，得到M和S；6) 计算h’=H(M)，并使用PUA采用RSA算法解密S，得到h；

7) 如果h’=h，则说明消息验证成功；否则，消息可能遭到篡改．

1.3 密钥管理

密钥分配过程(没有进行密钥分配或者需要更换密钥时)：

1) 公开自己的公钥 PUA，B公开自己的公钥PUB；

2) 使用PUB，采用RSA算法加密3DES算法的密钥K，生成数字信封DK；

3) 使用散列函数H，计算散列值h=H(DK)；

4) 使用私钥PRA采用RSA算法加密h，产生数字签名S；

5) 将S和DK一起发给B；

6) 用H计算h’=H(DK)，用PUA解密S，若h=h’，说明消息来自A没有被篡改；

7) 使用PRB解密DK，得到3DES算法的密钥K，完成密钥分配．

2 算法优化与数字签名

2.1 RSA算法优化

RSA算法是一种非常典型的公钥密码体制，具有安全性好和密钥管理方便等优点[13]．但是它也存在一些不足：一方面，计算密钥需要大量的计算，且在数据加密和解密过程中都需要计算某整数的模 n整数次幂问题，这些大量计算都消耗了大量的时间，限制了RSA算法的效率．另一方面，大素数p和q的确定没有一个成熟的方法，一般使用繁琐的素性检测和随机生成的办法产生大素数，效率较低[14]．

本文从下列几个方面对RSA算法进行优化：

1) 模算术里的求幂运算：在RSA中，加密和解密都需要计算某整数的模n整数次幂，如果先求出整数的幂，再对 n取模，那么中间结果会非常大．我们可以利用模算术的下列性质来计算

[(a mod n)×(b mod n)]mod n = (a×b)mod n (1)

这样我们将中间结果对n取模，简化计算：

假定要计算ab，其中a和b是正整数，将b表示为二进制数bkbk-1…b0，则：=∑ 2ibi≠0

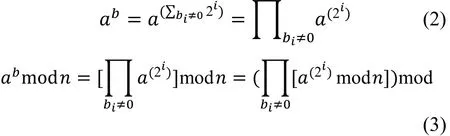
2) 用私钥进行有效运算：我们不能为了计算效率而简单地选择一个小数值的 d，为了简化计算，这里运用中国剩余定理来加快运算速度．

首先介绍中国剩余定理[15]，也叫孙子定理，是数论中最有用的定理之一．CRT(中国剩余定理)说明某一范围内的整数可通过它的一组剩余类数来重构，这组剩余类数是对该整数用一组两两互素的整数取模得到的[15]．令：

其中mi是两两互素的，我们可将ZM中的任一整数对应一个 k元组，该 k元组的元素均在m中，这种对应关系为：A↔(a1,a2,…,ak)，其中 A∈ZM，对1≤i≤k，ai∈m，且 ai=A mod mi．

定理 1：对 1≤i≤k，令 Mi=M/mi，因为 Mi=m1×m2×…×mi-1×mi+1×…×mk，所以对所有的 j≠i，有 Mi≡ 0(mod mj)．令

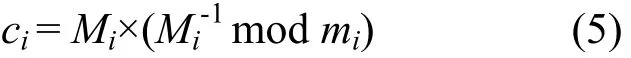
定理2：根据Mi的定义有Mi与mi互素，所以Mi有唯一的模 mi的乘法逆元，可以得到唯一的ci．计算

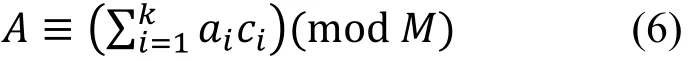
由于 j≠i时，cj≡ Mj≡ 0(mod mi)，且 ci≡ 1(mod mi)，故ai= A mod mi，上式得证．

由上两个定理可以方便求解M = Cdmod n，定义一些中间结果：Vp= Cdmod p, Vq= Cdmod q

运用CRT公式(5)～(6)，定义

进一步，使用费马定理来简化Vp和Vq的计算，即依据：如果p和a互素，则ap-1≡ 1(mod p)．

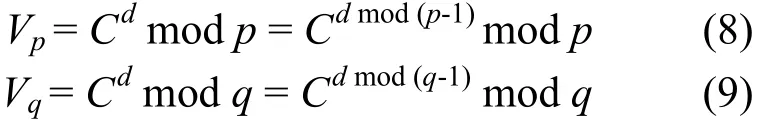
这里的d mod(p-1)和d mod(q-1)可以预先计算出来，与直接计算M = Cdmod n相比，上述的计算速度快了很多．

3) 大素数生成与检测：在文献[16]中已经证明随机递增搜索次数要小于随机搜索法，所以我们这里使用随机递增搜索法来产生大素数．由数论中的素数定理可知，在N附近平均每隔lnN个整数就有一个素数，这样我们在找到一个素数之前，平均要测试大约lnN个整数．由于偶数直接拒绝，所以实际上只需测试大约(lnN)/2个整数[17]．在进行素性检测前，我们可以先进行预处理以提升检测效率，排除掉偶数，使用小素数整除法进一步筛选，然后使用Miller-Rabin算法对伪素数的素性进行检测．多次执行测试可使得一个整数是素数的概率接近1.0．测试一个给定的数n是否为素数的过程涉及n和一个随机选择的整数a，a＜n．若n未通过测试，则n不是素数；若n通过了测试，则n可能是素数，也可能不是．若对许多随机选择不同的 a，n均能通过测试，则我们几乎可以相信n就是素数．这个方法看似有些繁琐，但是只有在需要一对新的密钥时才会执行这个过程，所以一般不会很频繁．

2.2 数字签名过程

RSA算法除了加解密外还可用于数字签名，进行身份认证．我们通过散列函数H可以生成一个散列值h作为消息认证码，h=H(M)[18]．其中M是需要传输的消息，H(M)是定长的散列值．使用散列函数作为认证码可以减少数据签名时间，增加效率．同时可以不泄露要签名的消息，提高保密度．签名过程如下：

1) 发送方将要发送的消息 M用过散列函数计算，产生散列值h=H(M)．

2) 发送方用自己的私钥加密h，产生数字签名S=hdmod n．

3) 发送方将消息M和签名S一同发给接收方．

4) 接收方用发送方的公钥解密签名 S得到h，再用散列函数H计算散列值h’．如果h’等于h，则说明消息来源正确，没有被篡改；否则，消息来源可能有问题．这样在消息传输过程中就避免了消息来源问题和中间人篡改消息的可能．

3 实验结果

本次实验的测试环境为：i5-4440 CPU、8G内存，操作系统为 Windows7，开发工具是 Visual Studio 2010．

3.1 RSA加密速率与签名效率测试

首先对素数生成效率进行测试，为了测试大量素数生成效率，素数为512位．改进算法与经典算法的效率对比如图 1．可以看出，五次实验随着生成素数的数量增加，消耗时间明显有所改善．通过改善生成素数时间可以提高RSA签名效率[19]．

测试RSA签名速率我们生成1 024位素数单独测试，并对比传统RSA签名和只有CRT的RSA签名．如图2所示，本文改进的签名计算过程有非常明显的效率提升，可以大幅度提高RSA加解密速度，使其可以有效的应用在大数据传输的消息认证中．

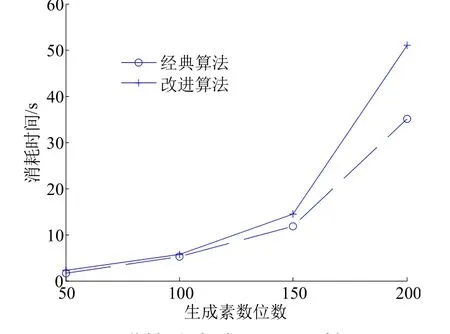
图1 改进算法生成大素数时间对比Fig.1 The comparison of generate large prime time

图2 RSA签名时间对比Fig.2 Comparison of RSA signature time

3.2 安全性分析

混合加密体系主要的安全风险在于密钥管理与消息认证．密钥管理风险是基于RSA算法的安全性上的，而RSA算法在模数够大(大于1 024 bits)时的安全性是有保证的．所以在体系下进行密钥分配和密钥更换时严格执行密钥管理方法，即可保证密钥管理过程中的安全．消息认证方面，我们没有直接使用消息进行数字签名，而是使用了散列函数H计算散列值．即使第三方攻击者获取发送方A的两个签名S1，S2．也不能计算出S3d=((S1dmodn)(S2dmodn))modn．因为给定一个D很难找到M，使得H(M)=D，这样就避免了第三者篡改、伪造签名和中间人攻击等风险．

4 结语

本文以校园一卡通系统为例，面对多校区分系统传输信息安全和密钥管理的需要，综合分析了目前主流的对称加密算法 3DES和非对称加密算法RSA．在对其功能过程进行分析的同时，优化部分计算过程，结合两个算法功能和运算的特点研究混合加密体系．解决系统的密钥管理与消息认证问题，提高系统运行安全性．对于分布式信息管理系统数据安全问题提出一种解决思路．

在后续的研究中，将会在实际系统中检测该体系的运行并推广到其他分布式信息管理系统．同时继续优化加密过程以提高运算速度，并在身份认证与消息认证方面做更深入的研究．

References

[1] 杨波. 现代密码学[M]. 北京: 清华大学出版社, 2007.YANG Bo. Modern cryptography[M]. Beijing: Tsinghua University press, 2007.

[2] 陈恭亮. 信息安全数学基础[M]. 北京: 清华大学出版社, 2011.CHEN Gongliang. Mathematical foundations of information security[M]. Beijing: Tsinghua University press, 2011.

[3] STALLINGS W. The advanced encryption standard[J].Cryptologia, 2010, 26(3): 165-188.

[4] JAMIL T. The rijndael algorithm[J]. Potentials, 2004,23(2): 36-38.

[5] RIVEST R L. The RC5 encryption algorithm[J]. Springer Berlin Heidelberg, 1995: 86-96.

[6] RIVEST R L, SHAMIR A. A method for obtaining digital signatures and public key cryptosystems[J]. Communications of the Association for Computer Machinery, 1978,21(2): 120-126.

[7] WIENER M J. Cryptanalysis of short RSA secret exponents[J].IEEE Information Theory Society, 1990, 36(3): 553-558.

[8] BONEH D, DURFEE G. Cryptanalysis of RSA with private key d less than N0. 292[J]. IEEE Information Theory Society, 2000, 46(4): 1339-1349.

[9] WANG Xiaoyun, YU Hongbo. How to Break MD5 and Other Hash Functions[J]. Cryptologia, 2005, 251(7): 357-362.

[10] 饶进平, 冯登国. 高速RSA处理芯片的研究与实现[J].计算机工程与应用, 2003, 39(5): 139-141.RAO Jinping, FENG Dengguo. Research and Implementation of High Speed RSA Crypto Chip[J]. Computer engineering and Applications, 2003, 39(5): 139-141.

[11] 王琴琴, 陈相宁. Montgomery算法在RSA中的应用及其优化[J]. 计算机技术与发展, 2007, 17(6): 145-146, 150.WANG Qinqin, CHEN Xiangning. Optimization and Application of Montgomery Algorithm in RSA[J]. Computer Technology and Development, 2007, 17(6): 145-146, 150.

[12] 王安. RSA 公钥密码算法的快速实现[D]. 济南: 山东大学, 2008.WANG An. Fast implementation of RSA public key cryptosystem[D]. Jinan: Shandong University, 2008.

[13] 贺克英. 改进的RSA算法实现研究[D]. 成都: 电子科技大学, 2010.HE Keying. Research and implementation of the improved RSA algorithm[D]. Chengdu: University of Electronic Science and technology of China, 2010.

[14] YEN Sungming, KIM Seungjoo, LIM Seongan. RSA Speedup with Chinese Remainder Theorem Immune against Hardware Fault Cryptanalysis[J]. IEEE Transactions on computers, 2003, 52(4): 461-472.

[15] 费晓飞, 胡捍英. CRT-RSA算法安全性分析[J]. 微计算机信息, 2009, 25(3): 38, 54-55.FEI Xiaofei, HU Hanying. Security of CRT based RSA Algorithm[J]. Micro computer information, 2009, 25(3): 38, 54-55.

[16] 张宝华, 殷新春. RSA密码算法的安全及有效实现[J].中山大学学报: 自然科学版, 2008, 40(6): 22-26.ZHANG Baohua, YIN Xinchun. The safe and efficient implementation of RSA algorithm[J]. ACTA Scientiarum Naturalium Universitatis Sunyatseni: Sci. &Tech. , 2008, 40(6): 22-26.

[17] 石井, 吴哲, 谭璐, 等. RSA数据加密算法的分析与改进[J]. 济南大学学报: 自然科学版, 2013, 27(3): 283-286.SHI Jing, WU Zhe, TAN Lu, et al. Analysis and Improvement of RSA Data Encryption Algorithm[J]. Journal of University of Jinan: Sci. & Tech. , 2008, 40(6): 22-26.

[18] 肖振久, 胡驰, 姜正涛. AES与RSA算法优化及其混合加密体制[J]. 计算机应用研究, 2014, 31(4): 1189-1194.XIAO Zhenjiu, HU Chi, JIANG Zhengtao. Optimization of AES and RSA algorithm and its mixed encryption system[J].Application Research of Computers, 2014, 31(4): 1189-1194.

[19] 刘学军, 邢玲玲, 林和平, 等. Miller-Rabin素数检测优化算法研究与实现[J]. 信息技术, 2008(12): 141-143.LIU Xuejun, XING Lingling. Research and realization of Miller-Rabin optimizing algorithm for prime testing[J].Information Technology, 2008(12): 141-143.