基于神经网络的交通发生量预测研究

孙 健，陈书恺，竺寒冰

（1. 上海交通大学船舶海洋与建筑工程学院， 海洋工程国家重点实验室，上海200240；2. 上海交通大学船舶海洋与建筑工程学院，上海 200240， 3. 大连海事大学交通运输管理学院，辽宁 大连 116026）

在城市交通规划中，交通发生吸引量预测作为传统交通规划四阶段的首要步骤，是城市规划布局与公共设施建设的重要参考依据[1]．纵观国内交通规划现状，大部分交通规划工作均从土地利用入手，建立不同土地利用类型与交通发生吸引量的预测模型，主要包括生成率模型、回归分析模型等[2-3]．然而，传统预测模型存在以下问题：（1）影响因素和交通发生吸引量并不是成完全的线性关系；（2）城市各区域发展水平存在差异，仅使用面积或人口数据进行预测会造成较大偏差；（3）分析模型考察因素过多，需要进行大量数据调查分析工作．

为了解决上述问题，国内外学者进行了大量的理论研究．Cervero和Kockelman[4]考察了在混合土地利用情况下，土地利用密度、多样性、布局等因素对不同出行目的交通需求的影响．Eliasson 和Mattsson[5]通过分析家庭住址对出行方式的影响，探讨了基础设施、家庭住址和交通需求的关系．石飞等[6]探讨了土地利用性质、规模和强度对出行产生的影响，提出的预测模型能充分考虑到城市中不同地区单位用地面积交通生成量的差别．近年来，随着智能算法的发展，越来越多的学者将人工神经网络与土地利用指标相结合以提高交通发生吸引量预测的准确性．冯树民和慈玉生[7]建立了基于出行产生量的四层BP神经网络预测模型，以不同土地利用面积百分比作为输入神经元，提高了预测模型的精度．杨荣英等[8]利用主成分分析法对输入变量进行预处理，利用各类影响因素的线性组合作为神经网络的输入变量，从而达到减少输入变量个数、简化模型结构的目的．

然而，在实际调查中往往只能得到小区的土地利用面积数据，难以度量土地利用强度和其他经济社会指标对交通生成量的影响．因此，有必要对交通小区进行分组，减小同组小区发展程度及土地利用强度差别．晏杰[9]通过K-means聚类方法根据住宅、人口等指标确定并且划分了家庭类型；邹志云等[10]对全国大中城市的经济指标进行了聚类分析，使用对居民出行强度相关性最大的指标建立回归模型．这些研究对区分不同类型交通小区具有较好的借鉴意义．

本文以大连市交通调查数据为例，旨在提出一种基于BP神经网络的预测方法，用以拟合不同土地利用面积和交通发生量的非线性关系．与传统研究方法相比，本文对交通调查数据进行预处理分析：引入了K-means聚类分析，使得同组小区拥有相近的人口、就业水平，减少同组小区的土地利用强度差异；并在聚类样本内进行主成分分析，通过计算各指标对主成分的贡献率，确定BP神经网络输入变量．针对各样本分别建立BP神经网络，对交通生成量进行预测分析．在此基础上，本文提出方法与传统回归模型进行了比较，发现基于数据预处理的BP神经网络具有较好的预测精度．

1 数据预处理

1.1 聚类分析

在对交通小区各项数据进行预处理时，聚类分析可将特性相似的交通小区划分为相同类别，从而减少同组内交通小区数据指标的差异性．本研究利用SPSS软件，通过K-means方法对现有数据进行聚类分析，其算法具体流程如下[9]：

(1)在数据标准化的基础上，根据数据特点，确定需要聚集的类别数．

(2)根据样本特征确定初始类别中心．

(3)利用欧式距离计算样本

Xi= ［xi1,xi2,…,xin］T到其初始样本中心Cr的距离，并将样本归入离它最近的类别中．其距离计算公式如下：

(4)计算各新类别的中心点坐标Cr=［cr1,cr2,…,crn］T，重新进行归类．其中，crn的计算公式为：

式中：mr是第r个聚类中心中样本个数．

如果本次计算的聚类中心点坐标正好与上一次中心坐标相重合，说明各个样本进入的类别合适；如果两次的类中心点坐标不同，说明聚类中心结果需要调整．

（5）重复步骤(3)-(4)，直至达到收敛标准．

1.2 主成分分析

主成分分析的基本方法是通过构造原变量适当的线性组合，产生一系列互不相关的新变量，并且含有尽可能多的原有信息，从而达到减少变量个数，简化模型的目的．考虑到交通小区调查会涉及到多方面数据如人口数、家庭户数、就业数、各类型土地利用面积等，有必要进行关联度分析，并在此基础上找出对主成分载荷率大的指标作为神经网络的输入变量．本文中主成分分析主要包括关联度分析和载荷率分析，具体分析计算过程如下[11]：

（1）计算各指标变量间的相关系数矩阵R:

式中：xkj为数据标准化后第k个样本的第j个指标变量，xj为第j个指标变量平均值．

（2）计算上述相关系数矩阵R的特征值和特征向量．在特征方程|λI-R|=0中，求出特征值λi（i=1,2,…,p），并按大小顺序排列，然后分别求出相应的正交单位化特征向量ei．

（3）计算第m个主成分的贡献率和累计贡献率．贡献率：

累计贡献率：

式中：p为指标个数．等式（4）计算主成分荷载率

1.3 数据处理与分析

以大连市交通出行调查和土地利用数据为例进行处理与分析[12]．整个大连市被分为169个交通小区，调查数据包括小区的人口数、就业数以及各土地利用面积指标．小区的土地利用类型分为三类：居住用地、工业用地、商业用地，所有数据通过ArcGIS平台进行统计筛选[13]．

首先对全市交通小区数据进行归一化处理，使得所有数据处于[0,1]的区间内，以消除数据量纲不一致的影响．去除残缺数据，共有156个小区数据有效．考虑到每个交通小区经济发展水平和土地利用强度的不平衡性，将人口、就业总量及单位面积的人口、就业量共计4个指标作为聚类分析的分组依据．为了保持各组内小区样本数量在合理区间内，通过逐次试验将聚类个数定为 4，最终各个类别中样本数比例见表1．

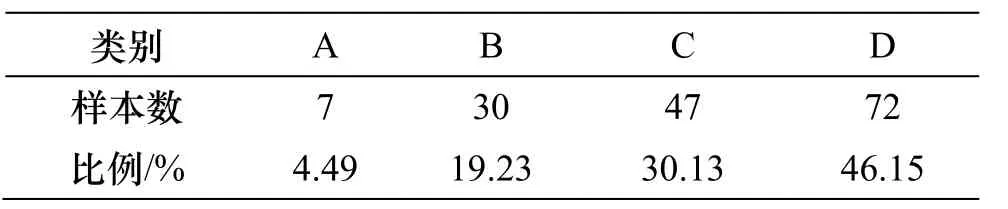
表1 每个类别中所包含小区数量Tab.1 Number of zones in each group

其中，按照人口以及就业数量由多到少进行排列可将各组分为 A～D组．将聚类结果在大连市交通小区分布图中标注．如图1所示，大连市城区由外到内逐步分为D至A组，其中D组小区主要处于城市郊区，C组小区处于过渡区域．市中心主要由B组及A组小区组成，该结果与大连市城区经济聚集分布状况基本吻合，可认为上述聚类分组结果是合理的．

图1 聚类结果分布Fig.1 Clustering analysis result of 169 zones in Dalian

以B、C组交通小区作为算例，对人口、就业、家庭户数、居住、商业、工业面积共计6个指标进行主成分分析．基于数据标准化结果，利用 SPSS软件计算得到相关系数矩阵．在两组交通小区中，家庭户数和人口数的相关系数均在0.9以上，其余指标间的相关系数在0.6以下．在此基础上进一步计算相关矩阵的特征值、主成分贡献率和累计贡献率．结果如表2．

主成分贡献率表示该主成分反映原始数据的信息量大小．由表2可看出在B组小区中，第一个主成分是方差贡献最大的主成分，前3个主成分解释了所有变量84.4%的信息量且特征值均大于1．对C组交通小区进行类似分析，同样可提取3个主成分来代替原变量指标分析其主成分载荷率．通过计算主成分载荷率（表3），可知在B组小区中，家庭户数和人口数对第一主成分的载荷率都超过 90%，而居住用地面积可解释主成分中80.3%的信息量；商业用地面积对第二主成分的载荷率为80.5%；工业用地面积占第三主成分信息量最大．考虑到家庭户数与人口数的高相关性，可舍去家庭户数指标简化计算．由此，B组小区交通发生量预测模型的输入变量为人口数以及三种土地利用面积．对于C组交通小区，考虑到居住用地面积对第一主成分贡献率有所下降，而其余主成分中载荷量较大的指标与B组交通小区基本相同，因此采用人口以及工业、商业用地面积作为C组神经网络的输入变量．

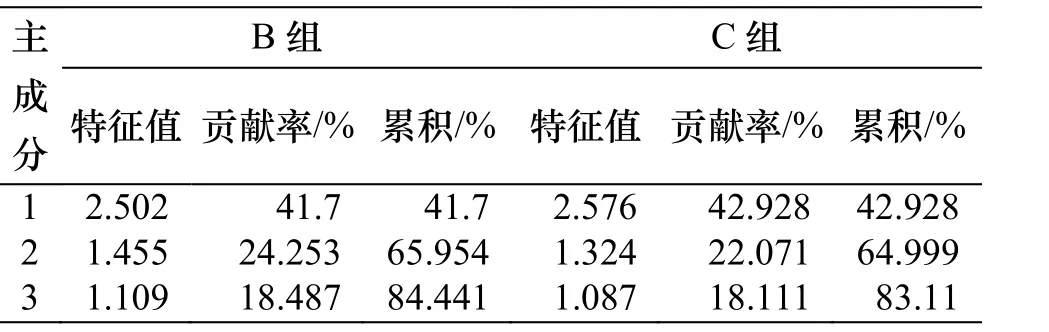
表2 主成分特征值及其贡献率Tab.2 Characteristics of values and contribution of three principal components

表3 主成分载荷率矩阵Tab.3 Matrix of loading rate to principal components

2 交通发生量预测

2.1 BP神经网络模型

BP神经网络属于非参数回归模型，具有结构简单、使用方便等特点[14-16]，已在通信、交通行业得到广泛应用．通过对训练样本数据的学习，BP神经网络能够很好地反映对象输入及输出之间复杂的非线性关系．只要有足够的隐含层和隐含节点，BP网络就可逼近任意的非线性函数．基于以上优点，本文采用该模型预测B组和C组样本小区的交通发生量．

在上述B组、C组中各随机抽取21个交通小区作为样本一、二分别建立BP神经网络，其中12组为训练组数据，9组为测试组数据．依据上文结论，样本一BP神经网络输入变量为人口数和三种土地利用面积，样本二BP神经网络输入变量为人口数和工业、商业用地面积，输出变量均为交通发生量．一般来说，一个由输入层、隐含层、输出层组成的3层BP神经网络即可完成任意n维至m维函数的映射及输出．考虑到土地利用与交通发生量之间关系较为复杂，并且数据量较大，本文设置 2个隐含层以加强隐含层与输入输出层连接性，同时加快神经网络训练速度[5]．两个隐含层中神经元个数l相同，可根据经验公式确定[14]．

式中：m与n分别为输入神经元数目与输出神经元数目，a为1～10范围内参数．

通过逐个比较隐含层神经元个数对训练速度和精度的影响，得出当隐含层神经元个数为10时，误差较小并且训练时间较短．因此，对于样本一建立输入层节点为4，隐含层节点为10，输出层节点为1的BP神经网络；样本二中BP网络除了输入层节点数为 3，其余参数设置同样本一 BP网络．使用 MATLAB神经网络工具箱设置函数参数时，训练误差目标均设定为0.001．BP神经网络隐含层转移函数分别选取双曲正切型和对数型函数，输出层采用线性转移函数，MATLAB中分别利用 tansig、logsig和purlin函数实现，其设定方法可参考文献[7]和[14]．为了避免训练过程陷入局部最小值，采用带动量的批处理梯度下降法，并通过traingdm命令实现．由于采集数据单位不一致，利用 MATALB中 premnmx命令对输入数据进行归一处理，并对输出数据进行反归一处理即可得到预测值．

用训练组数据训练各自样本的BP神经网络，其训练及误差变化如图2所示，两个BP神经网络分别在训练次数到451步和178步时收敛．将9组测试数据输入BP神经网络进行预测，其中测试结果如表4所示．

图2 神经网络训练及误差变化Fig.2 BP neural network training process and error changes

由表5可知，除了样本二中个别小区的误差较大之外，其余小区的预测精度均在可接受范围内．因此，样本二中省略居住面积作为输入变量没有神经网络性能产生较大影响．其中，样本一平均预测误差为9.1%，样本二平均误差为11.7%．针对个别小区预测误差仍然较大的问题，说明交通发生量还受区位、基础设施等其他因素的影响．

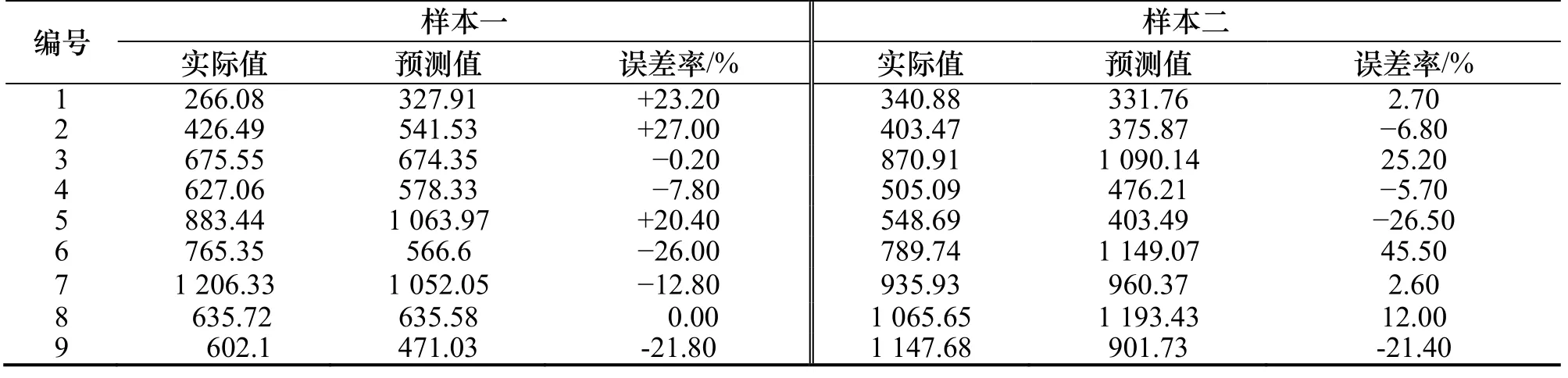
表4 样本一及样本二神经网络预测结果Tab.4 Testing results of BP neural network in samples 1 and 2

2.2 对比分析

为了比较BP神经网络与传统线性回归方法的预测精度，检验数据预处理对BP神经网络预测精度的提高效果，本文以样本一交通小区为例，设计对比试验进行分析．在对比分析中，首先建立多元线性回归模型进行预测．以样本一训练组中交通小区的三种土地利用面积，即居住用地、工业用地及商业用地为自变量，交通发生量为因变量建立多元线性回归模型，该回归模型的相关系数为：

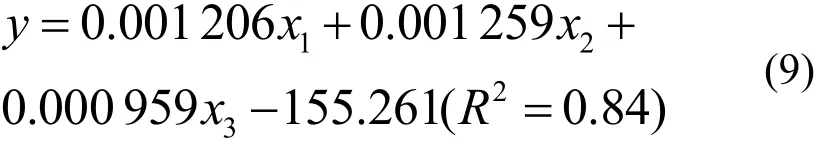
式中： y为交通发生量（百次/天）；x1, x2, x3为居住用地、工业用地、商业用地面积（m3）

以式(9)的多元线性回归方程计算样本一测试组小区交通发生量大小，结果如表5所示．

此外，假设不对交通小区进行聚类分析和主成分分析，以上述两个样本中所有训练数据建立单一BP神经网络进行对比分析．该BP神经网络输入变量为家庭户数、人口数、就业数及三种土地利用面积，输出变量为交通发生量，其他参数设定同2.1．利用新建立的BP神经网络计算样本一中测试组小区交通发生量大小，结果如表5所示．

表5 样本-对比结果Tab.5 Comparison results in Sample 1

如表5所示，虽然回归模型建立在小区分组基础上，但其预测精度明显低于在数据预处理基础上建立的BP神经网络．主要原因在于回归模型不能较好拟合土地利用与交通发生量的非线性关系．若不对数据进行预处理分析直接建立单一的BP神经网络，其预测精度也将明显下降．这表明经过聚类分析后的同组样本差距较小，以此建立的BP神经网络可靠性较高，能够较好反映同组小区土地利用对交通发生量影响特点．因此，提高交通发生量预测可从以下两方面入手：1. 数据预处理，减小同组小区差异，选择合理预测输入变量，减少数据冗余；2. 合理选择预测模型，有效拟合各影响因素与交通发生量的非线性关系．

3 结语

（1）本文以大连市交通调查数据为例，通过聚类分析和主成分分析对交通小区土地利用、人口、就业等数据进行预处理，并在此基础上建立BP神经网络预测交通发生量大小，最后将预测结果与传统回归预测方法进行了对比．

（2）结果表明，聚类分析可减少同组交通小区之间差异性；主成分分析能够为选择模型输入变量提供依据．在数据预处理基础上建立的BP神经网络预测精度优于传统多元回归模型，同时也优于未经过数据预处理建立的BP神经网络．

（3）由于城市交通小区数量较大，社会经济发展程度不尽相同，实际影响交通发生量的因素较多．受调查数据的限制，文中只选取了几类相对重要的指标建立预测模型，导致模型存在一定的局限性．在今后的研究实践中，应在数据预处理的基础上充分考虑道路设施、区位等其他因素对交通发生量的影响，从而进一步提高预测精度．

References

[1] 薛睿, 张建华, 孙健. 公交服务可靠性研究[J], 武汉科技大学学报:自然科学版, 2014, 37(5): 391-396.XUE Rui, ZHANG Jianhua, SUN jian. Reliability of public transit service [J]. Journal of Wuhan University of Science and Technology, 2014, 37(5): 391-396.

[2] 孙健, 章立辉, 彭春露, 等. 基于元胞自动机的城市土地利用预测模型研究-以美国Florida州Orange County为例 [J]. 交通运输系统工程与信息, 2012, 12(6):85-92.SUN Jian, ZHANG Lihui, PENG Chunlu, et al.CA-based urban land use prediction model: a case study on Orange County, Florida, U. S. [J], Journal of Transportation Systems Engineering and Information Technology 2012, 12(6): 85-92.

[3] 石飞, 王炜, 陆建. 居民出行生成预测方法的归纳和创新[J]. 城市交通, 2005, 3(1):43-46.SHI Fei, WANG Wei, LU Jian. Improvement and conclusion about resident trip generation[J]. Urban transport of China. 2005, 3(1):43-46.

[4] CERVERO R, KOCKELMAN K. Travel demand and the 3Ds: density, diversity, and design [J]. Transportation Research Part D: Transport And Environment, 1997,2(3): 199-219.

[5] ELIASSON J, MATTSSON L G. A model for integrated analysis of household location and travel choices [J].Transportation Research Part A: Policy and Practice,2000, 34(5): 375-394.

[6] 石飞, 江薇, 王炜, 等. 基于土地利用形态的交通生成预测理论方法研究[J]. 土木工程学报, 2005, 38(3):115-118.SHI Fei, JIANG Wei, WANG Wei. Research on forecast method for traffic creating based on characteristic of land utilizing [J]. China Civil Engineering Journal, 2005,38(3): 115-118.

[7] 冯树民, 慈玉生. 居民出行产生量 BP 神经网络预测方法[J]. 哈尔滨工业大学学报,2010,42(10): 1624-1627.FENG Shumin, CI Yusheng. A forecast method for trip generation based on BP neural network [J]. Journal of Harbin Institute of Technology, 2010, 42(10): 1624-1627.

[8] 杨荣英, 苗张木, 沈成武. BP 神经网络主成分分析法在交通需求预测中的应用[J]. 武汉理工大学学报:交通科学与工程版, 2002, 26(6): 386-388.YANG Rongying, MAIO Zhangmu, SHEN Chengwu.Application of principal component analysis method in BP Neural network to traffic demand and prediction [J].Journal of Wuhan University of Technology:Transportation Science & Engineering, 2002, 26(6):386-388.

[9] 宴杰. 聚类分析在家庭划分中的应用方法[J]. 交通运输工程系统工程与信息, 2007, 7(1):137-142.YAN Jie. The application of cluster analysis approach to family’s type division [J]. Journal of Transportation System Engineering and Information Technology, 2007,7(1):137-142.

[10] 邹志云, 蒋忠海, 梅亚南, 等. 大中城市居民出行强度的聚类分析[J]. 交通运输工程与信息学报, 2007,5(2):8-13.ZOU Zhiyun, JIANG Zhonghai, MEI Yanan, et al.Cluster analysis on the trip intensity of residents in large and medium city [J]. Journal of Transportation Engineering and Information, 2007, 5(2): 8-13.

[11] 龙东华, 邵毅明, 向红艳. 基于神经网络的停车需求预测模型及应用[J]. 交通信息与安全, 2010, 28(5): 6-9.LONG Donghua, SHAO Yiming, XIANG Hongyan.Parking demand forecasting model and its application based on neural network [J]. Journal of Transportation Information and Safety, 2010, 28(5): 6-9.

[12] 谭晓雨. 土地利用与交通小区发生吸引量关系研究[J].物流技术, 2012, 31(4):33-37.TAN Xiaoyu. Study on relationship between land use and community-based traffic generation and attraction [J].Logistics Technology, 2012, 31(4):33-37.

[13] 孙健, 刘琼, 彭仲仁. 城市交通拥挤成因及时空演化规律分析-以深圳市为例, 交通运输系统工程与信息,2011, 11(5): 86-93.SUN Jian, LIU Qiong, PENG Zhongren. Research and analysis on causality and spatial-temporal evolution of urban traffic congestions-a case study on Shenzhen of China [J], Journal of Transportation Systems Engineering and Information Technology, 2011, 11(5): 86-93.

[14] 卓金武, 魏永生. Matlab在数学建模中的应用[M]. 北京: 北京航空航天大学出版社, 2011.ZHUO Jinwu, WEI Yongsheng. MATLAB in mathematical modeling[M]. Beijing: Beihang University Press, 2011.

[15] RUMELHART D E, MCCLELLAND J L. Parallel distributed processing: explorations in the microstructure of cognition [M]. The MIT Press, Cambridge, MA. 1986.

[16] ZHANG L, PENG Z, SUN D J, et al. Rule-based forecasting of traffic flow for large-scale road networks[J].Transportation Research Record: Journal of the Transportation Research Board, 2012, 2279: 3-11.