基于线形和限速的施工瓶颈路段通行能力改善方法
陈 君 ,魏贤鹏,陶 珂,赵雪君
(西安建筑科技大学土木工程学院,陕西 西安710055)
随着城市化速度的加快,交通基础设施建设的步伐也随之加快.其中,旧路的改建、扩建以及城市轨道线路的新建是交通基础设施建设的重要组成部分.施工期间在道路上设置作业区,占用道路资源,极易诱发交通拥堵,成为道路交通瓶颈之一.
国内外学者对瓶颈路段的交通特性、通行能力、改善措施等做了大量研究.Enberg A和Mannan M S通过高速公路施工区交通流特性的研究表明施工区限速对车辆的运行速度和车头时距有明显的影响[1].Matthew等利用分层树回归法量化了道路特性对事故率的影响,研究表明道路线形以及路面状况是交通事故的最主要因素[2].美国的 MUTCD(Manual on Uniform Traffic Control Devices for Streets and highways)[3]和HCM(Highway Capacity Manual)[4]道路施工区域的交通组织和通行能力进行了系统全面的研究.国内学者刘小明对瓶颈上游溢流情况的影响进行了研究,得到通过改变交叉口信号相序避免溢流情况发生需要满足的条件[5].弓晋丽[6]等根据交通参数关系拟合后得到拥挤阈值,对交通参数时空变化图进行瓶颈位置识别,研究瓶颈附近交通拥挤特征,为交通管理、道路改造提供服务.同济大学张剑[7]等提出了快速路瓶颈失效的生存分析模型,利用该方法可精细化确定瓶颈点概率通行能力,并为快速路交通管理措施设计提供理论依据.以上主要从交通流特性、道路线形、通行能力等方面对瓶颈路段交通状况进行研究.然而,单纯的从某一方面入手不能有效地改善瓶颈路段拥堵状况.本文综合考虑道路线形、交通管理、交通流特性等因素,对瓶颈路段线形进行优化,并应用变道超车模型,提出有效提高瓶颈路段通行能力的方法,对改善瓶颈路段交通拥堵,提高交通系统服务水平有重要意义.
1 研究数据采集
1.1 实验路段概况
选取西安市长安南路与小寨东路交叉口东进口某段作为研究对象,由于地铁施工围挡,在该路段形成明显的交通瓶颈,由东向西车道由原来的三车道变为两车道,围挡区域离交叉口400 m.路段基本信息如图1,摄像机距道路边缘水平距离5 m,垂直距离为13层楼高(约40 m).
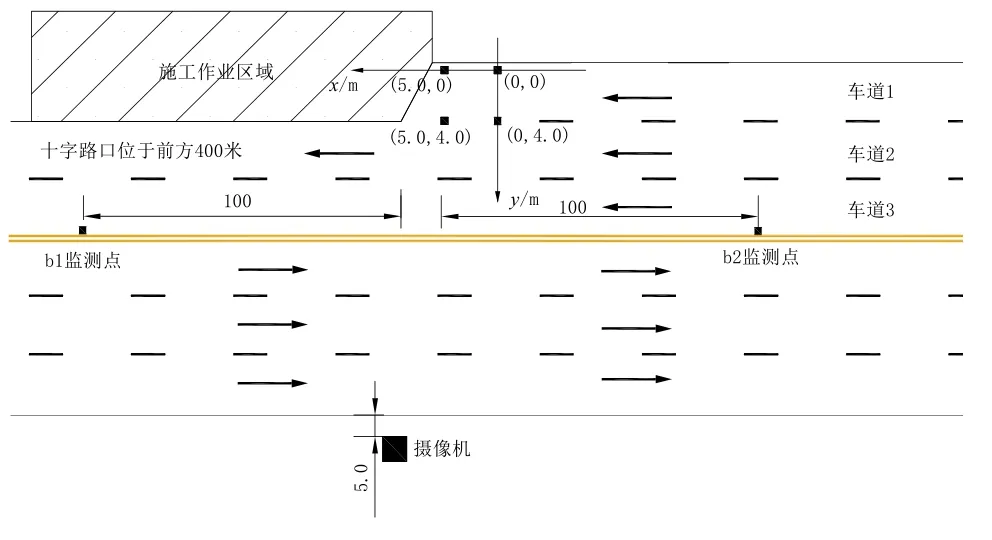
图1 基本路况俯视图Fig.1 The vertical view of the basic road
1.2 数据采集
1) 首先在待测路段布置四个特征点,并建立地面坐标系(如图1),给出四个点的地面坐标,分别为(0,0),(0,4.0),(5.0,0),(5.0,4.0);
2) 通过实地观测获取视频交通数据,用Matlab软件将视频转化为jpg格式,以不影响轨迹特征为原则,以每秒2张的速率获取356张图片,取第一帧图片获取图片中特征点的视频坐标;
2 围挡线形设计
速度是影响道路通行能力的重要因素,而线形是决定车辆实际运行速度的基础.目前,施工作业区围挡的线形存在盲目性、随意性,严重影响路段道路通行能力.同时,施工瓶颈附近也是交通事故易发区,交通事故的发生会加重交通拥堵程度.因此,施工区围挡线形优化设计对提高路段通行能力,保证行车安全具有实际意义.
2.1 车辆行驶轨迹数据分析
如图 2~3所示,分别为高峰和平峰条件下,车辆行驶轨迹图.同类型的车辆在不同时间段里轨迹不同,不同类型的车在同一时间段里运行的轨迹也不同,主要区别见表1.
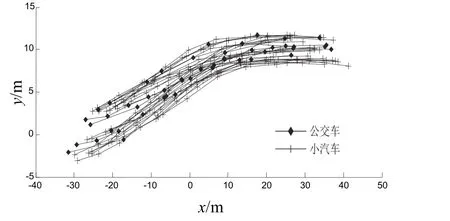
图2 平峰行车轨迹Fig.2 Flat peak traffic track
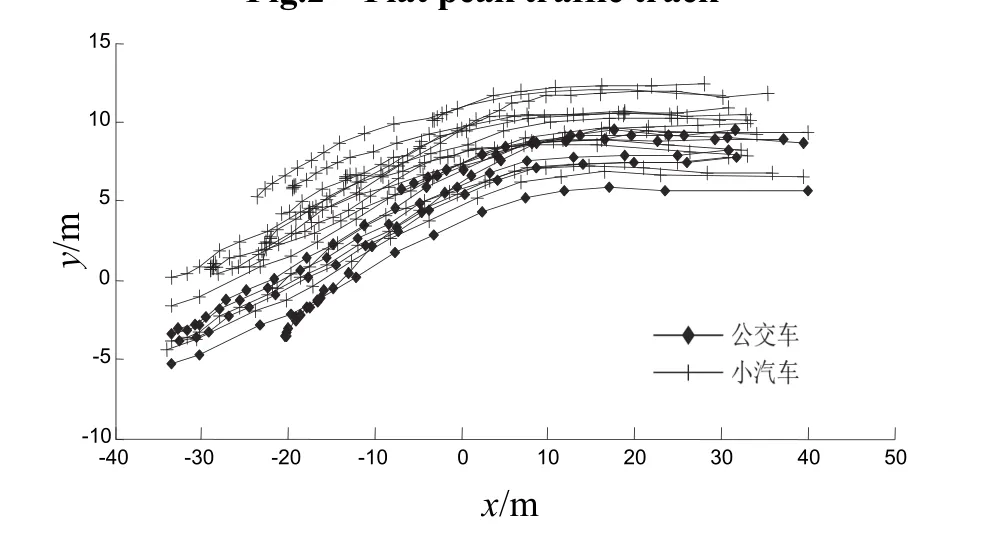
图3 高峰行车轨迹Fig.3 Peak traffic track

表1 行车轨迹分析Tab.1 Driving trajectory analysis
2.2 特征轨迹拟合
2.2.1 K-means聚类
用Matlab对车辆运行轨迹分析,采用K-means聚类算法对车辆轨迹聚类结果如图 4.K-means算法采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大.图4中类型的点代表不同的族,每个族有自己的质心点,该点是本族区域的核心.当车辆行驶到该区域时,以最大的概率通过质心,所以选质心点作为待求线形特征点是科学合理的.
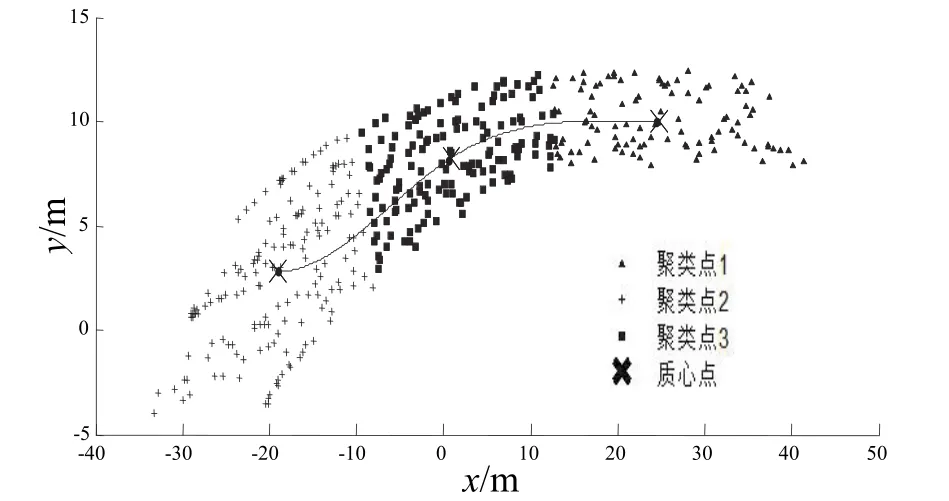
图4 K-means聚类结果Fig.4 K-means clustering results
车辆行驶在瓶颈路段的不同位置运行特征不同.在驶入瓶颈路段前,车辆一般会减速行驶,在车道1的车辆会伴随变道行驶.当车辆完全驶入瓶颈路段时,会保持较低速度匀速行驶.当车辆驶离瓶颈路段时会加速前进.因此,本文针对瓶颈路段车辆运行特性,选择三个聚类质心点对应三个不同路段车辆运行特性,这样能够客观地反映车辆运行特征,三个聚类质心点坐标如表2.

表2 聚类质心点坐标Tab.2 Cluster mass center’s coordinates
2.2.2 三次样条函数拟合
以聚类质心点为曲线特征点,运用三次样条函数[9]对车辆轨迹拟合,运用Matlab软件对聚类质心拟合结果见式(1).

三次样条函数所给定区间内一阶和二阶导数都存在,有效的保证了曲线光滑性,能够保证车辆在该线形上行驶的舒适性,且该线形变化缓慢,给驾驶员提供充足的变道心理准备,保证驾驶安全.
3 安全变道限速值的确定
城市道路道路交通事故不仅会造成严重的经济损失,还会导致交通拥堵.一旦某个路段发生交通事故,不仅影响本路段运行效率,还会影响附近路网运行效率.而围挡施工瓶颈路段涉及车辆加速、减速、变道超车等多种交通行为,交通行为构成复杂,极易引发交通事故.因此,考虑交通安全,减少交通事故的发生在施工围挡瓶颈路段的改善中有重要作用.本文在上文优化线形的基础上,确定出车辆安全运行的的限速值,其思路为:首先给出车辆变道转角,其次计算车辆在瓶颈路段安全跟驰距离,最后由安全变道约束条件得出安全限速值.
3.1 车辆变道转角的确定
为了保证车辆转弯与道路线性相适应,需建立车辆转角与线形之间的关系.其中车辆在变道时,转角不断变换,如图5所示.设原行驶方向为正方向,从开始转角时到最大值,从最大转角到为零,最后按原方向行驶[10].在变道过程是连续顺畅的,因此转角也是连续顺畅,转角的推算见式(2)~(3).
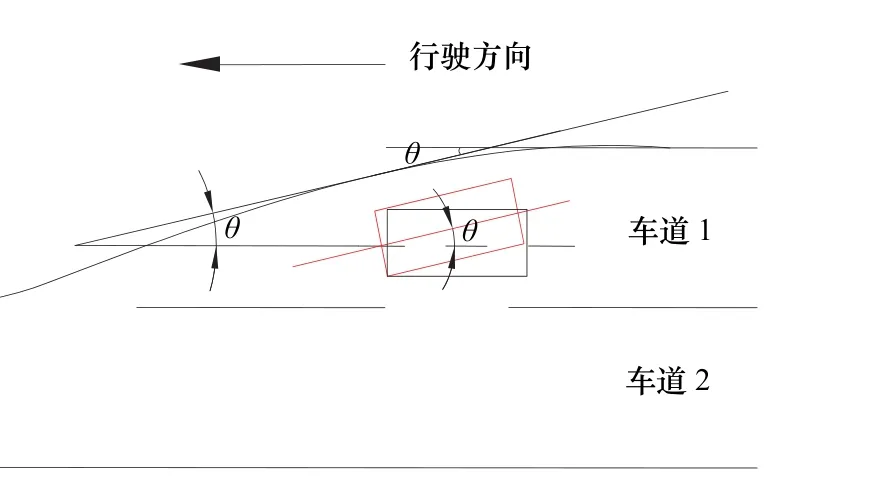
图5 变道转角示意图Fig.5 The sketch of changing lanes corner
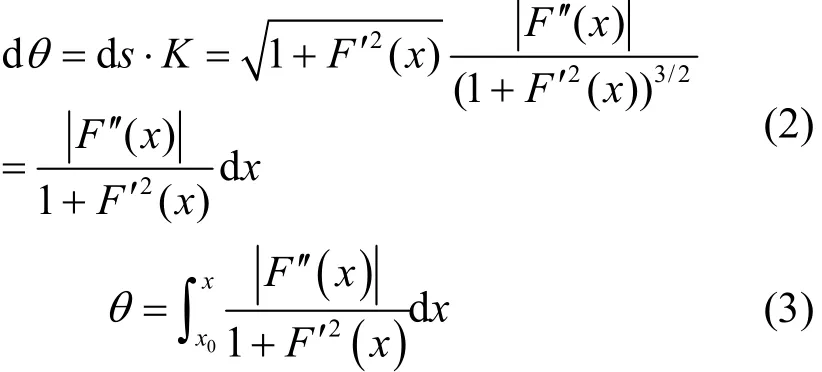
其中:θ为车道变换转角;ds为弧微分(平面曲线弧微分公式为 dK为曲率(二阶可导曲线的曲率公式为x0为线形起点的横坐标.
3.2 车辆安全跟驰距离确定
(1) 单车道安全跟驰距离.车辆在单线上行驶时,安全跟驰距离不仅与车辆制动性能有关,还与前后车辆行驶速度、驾驶员反应时间等多种因素有关.为了使安全跟驰距离更符合实际情况,引入跟驰车辆减速度增长过程[11],避免传统安全距离模型中减速度突变导致安全距离扩大问题.由于车辆行驶到瓶颈路段时,驾驶员一般会发生减速变道行为,所以此时跟驰车车速小于前导车车速,车辆安全跟驰距离[12]见式(4).
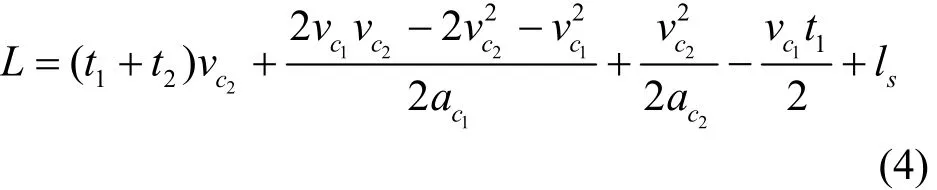
其中:L为车辆安全跟驰距离,m; t1为跟驰车辆减速度的增长时间,s;t2为反应时间,s; vc1、 vc2分别为前导车与跟驰车的行驶速度,m/s; ac1、 ac2分别为前后两辆车的最大制动减速度,为车辆停止后两辆车之间的安全距离,m;
(2) 车辆变道安全跟驰距离.如图 6所示,车辆在瓶颈处由车道1变到车道2过程中,变道安全跟驰距离d[13]由单车道安全跟驰距离和车辆因转弯所凸出的部分组成,其数学表达式见式(5).
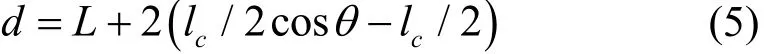
其中:d为车辆变道安全跟驰距离,m;cl为车辆长度,m;
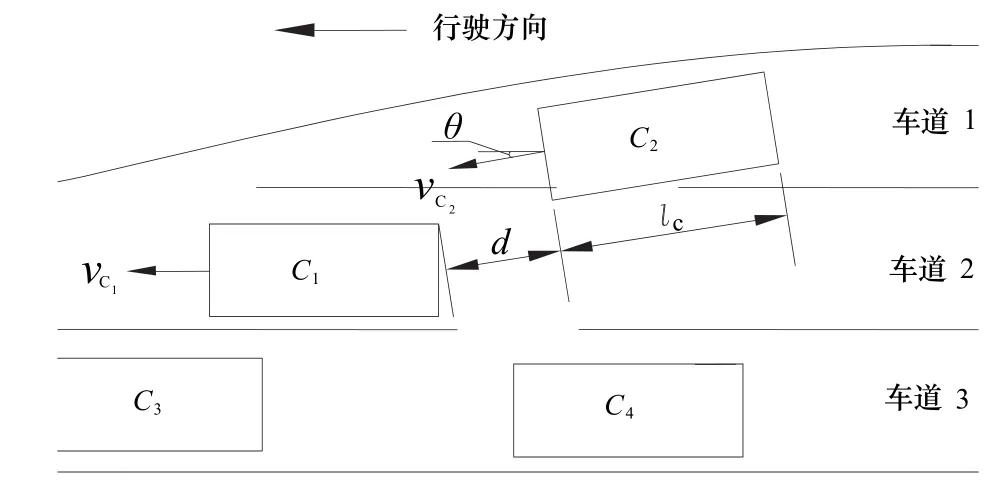
图6 变道跟驰距离示意图Fig.6 The sketch of lane change distance of car-following
3.3 速度约束条件
充分考虑车辆在跟驰行驶中的安全距离,保证车辆1c不与旁边车道车辆2c发生侧刮,需要满足约束条件如式(6)[13].
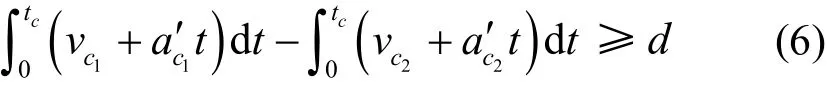
其中:t为换道花费时间(变量,s;1ca′、2ca′分别为车辆1c、2c的加速度,2m/s;ct为换道完成所用时间(常量),
别表示线形起、终点的横坐标;
3.4 安全变道限速值计算
安全变道限速值由式(6)推导求得,将式(4)~(5)代入整理得到关于2cv的表达式如下:
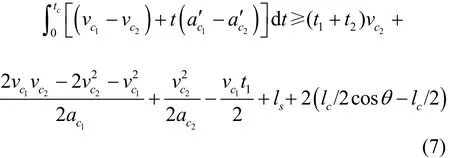
其中 tc由式6中的表达式算得转角θ由式(3)算得最大值为θmax= 2 6.1°,其他参数取值见表3.
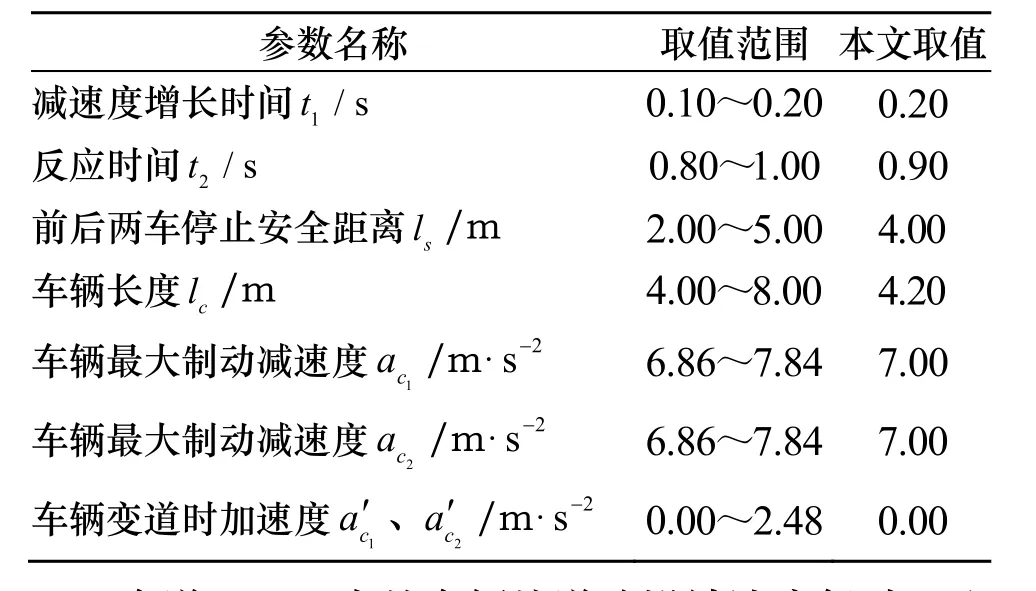
表3 参数取值表Tab.3 Parameter Value Table
车道 2、3中的车辆按道路设计速度行驶,取vc1= 6 0 km/h,将表3中已知参数值代入式7得到vc2满足不等式v解得 vc2≤12.66 m/s,即 vc2≤45.58 km/h,由于该路段靠近交叉口,车速偏低,所以取 vc2= 4 0km/h作为该车道安全限速管理值.
4 仿真评价
根据以上计算结果,对车道1采取限速措施(在距围挡区 15 m处设置限速牌),限速值为vc2=40 km/h,取限速值为30 km/h 、40 km/h、50 km/h进行对比评价,其他车道按设计车速60 km/h限速.并以公式(1)给出的线形作为道路围挡边界.在瓶颈路段设置变道标线,如图7所示,车道2相对于车道1有优先权,车道1的车辆在满足约束条件时可以变道到2车道行驶,否则等待变道时机.由此规则建立Vissim仿真模型,对本文提出的优化线性和限速措施进行评价,仿真界面见图 8,延误评价结果见图9,其他评价指标见表4.
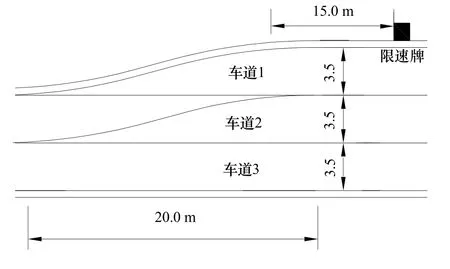
图7 渠化道路图Fig.7 The channelization of the road map

图8 优化路段仿真图Fig.8 The simulation diagram of road optimization
由图9仿真结果可知,交通量小于2000 veh/h时,行车延误比较小,车辆是自由行使状态,随着交通量的增大,行车延误都逐渐增大,但不同道路线形、不同限速值对应的延误不同.首先,在相同限速条件下,采用设计的道路线形渠化瓶颈路段对本路段的通行能力有显著提高,主要是因为优化后的道路线形能够提醒驾驶员提前变道,使车辆行驶到瓶颈处时无需采取变道行为能够连续、迅速通过瓶颈,避免车辆在瓶颈处产生紊乱排队现象,增加了整体运行效率.其次,在道路渠化前,平均行车延误随着限速值的增大,延误逐渐变小,但仍然大于道路优化后的平均行车延误.而采用渠化后的道路评价,当限速值为 vc2= 4 0 km/h时,延误最小,所以采用设计道路渠化线形和安全管理限速值能够显著改善瓶颈路段的行车效率.
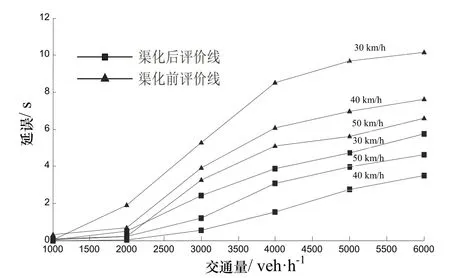
图9 优化前后车均延误对比图Fig.9 The average delay comparison chart before and after optimization
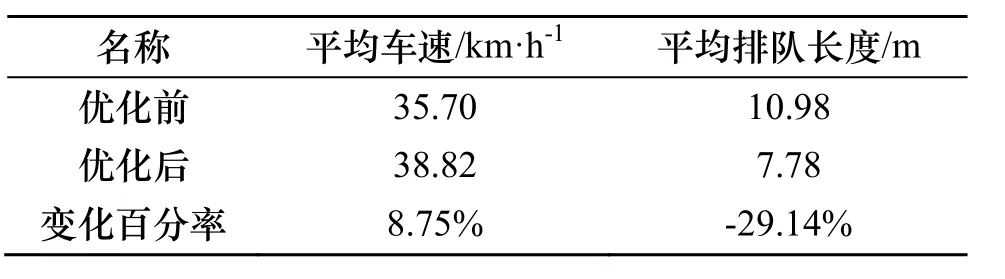
表4 仿真评价结果Tab.4 The evaluation results of simulation
如表4给出了采用道路设计线形渠化道路和限速值为40 km/h时其他参数评价结果,平均车速提高8.75%,平均排队长度减少29.14%.可见设计的道路线形和限速管理措施对提高道路瓶颈路段道路通行能力有明显效果,可以为交通管理部门提供科学的管理依据.
5 结论
(1) 分析了车辆运行规律,采用K-means聚类算法找出特征点,拟合得出车辆在瓶颈路段变道优化线形.
(2) 建立了与变道优化线形相适应的车辆安全变道模型,求解模型并得出安全限速管理值.
(3) 应用Vissim仿真软件综合评价了变道优化线形和安全限速管理措施的改善效果,评价结果表明:优化后的道路线形和安全限速管理措施能够有效提高该路段通行能力,可以应用到施工围挡瓶颈路段交通通行能力改善中.
References
[1] EENBERG A, MANNAN M S. Capacity and Traffic Characteristics at A Freeway Work Zone in Finland[C].Third International Symposium on Highway Capacity.Copenhagen, Danmark, Revised. 1998: 397-442.
[2] MATTHEW G. Karlaftis, GOLIAS Ioannis. Effects of road geometry and traffic volumes on rural roadway accident rates[J]. Accident Analysis and Prevention.2002.(34)357-365.
[3] Federal Highway Administration. Manual on uniform traffic control devices for streets and highways(MUTCD)[S]. Washington DC, U. S: Department of Transportation, 2003.
[4] Transportation Research Board Highway Capacity Manual: 2000[M]. Washington DC: Transportation Research Board, 2000.
[5] 刘小明, 郑淑晖, 钟剑. 交通瓶颈下相序设置对路口交通状况影响分析[J]. 公路交通科技, 2008, 25(7):122-127.LIU Xiaoming, ZHENG Shuhui, ZHONG Jian. Analysis of Effect of Phase Order Setup on Traffic at Intersection under Traffic Bottleneck[J]. Journal of Highway and Transportation Research and Development, 2008, 25(7):122-127.
[6] 弓晋丽, 杨东援. 基于检测线圈数据的道路交通瓶颈分析[J]. 公路交通科技, 2010, 27(7): 118-122.GONG Jinli, YANG Dongyuan. Analysis of Road Traffic Bottleneck Based on Loop Detector Data[J]. Journal of Highway and Transportation Research and Development,2010, 27(7): 118-122.
[7] 孙剑, 张娟. 城市快速路瓶颈交通流失效生存分析[J].同济大学学报: 自然科学版, 2013, 41(4): 530-535.SUN Jian, ZHANG Juan. Survival Analyses of Traffic Flow Breakdown at Urban Expressway Bottlenecks[J].Journal of Tongji University: Natural Science, 2013,41(4): 530-535.
[8] 刘博航, 裴玉龙, 徐慧智. 基于视频处理的车道变换轨迹获取技术[J]. 哈尔滨理工大学学报, 2007, 12(3):7-11.LIU Bohang, PEI Yulong, XU Huizhi. Lane-changing Track Access Technology Based On Video[J]. JOURNAL HARBIN UNIV. SCI. &TECH, 2007, 12(3): 7-11.
[9] 杨鹏. 样条曲线在道路平面线形中的应用研究[D]. 重庆: 重庆交通大学, 2011.YANG Peng. The spline curve study of highway horizontal alignment design[D]. Chongqing: Chongqing Jiaotong University, 2011.
[10] 裴玉龙, 张银. 车道变换期望运行轨迹仿真[J]. 交通与计算机, 2008, 26(4): 68-71.PEI Yulong, ZHANG Yin. Lane-changing Virtual Desire Trajectory Simulation[J]. Computer and Communications,2008, 26(4): 68-71.
[11] 许伦辉, 罗强, 吴建伟. 基于最小安全距离的车辆跟驰模型研究[J]. 公路交通科技, 2010, 27(10): 96-100.XU Lunhui, LUO Qiang, WU Jianwei. Study of Car-following Model Based on Minimum Safety Distance[J]. Journal of Highway and Transportation Research and Development, 2010, 27(10): 96-100.
[12] 许伦辉, 罗强, 傅惠. 基于前车制动过程的车辆跟驰安全距离模型[J]. 广西师范大学学报: 自然科学版,2010, 28(1): 1-5.XU Lunhui, LUO Qiang, FU Hui. Car-following Safe Distance Model Based on Braking Process of Leading Vehicle[J]. Journal of Guangxi Normal University: Natural Science Edition, 2010, 28(1): 1-5.
[13] 柏伟, 李存军. 基于不同限速条件下的超车模型研究[J]. 交通运输系统工程与信息, 2013, 13(2): 63-68.BAI Wei, LI Cunjun. Overtaking Model Based on Different Limiting Speed[J]. Journal of Transportation Systems Engineering and Information Technology, 2013,13(2): 63-68.

