未知杂波背景下恒虚警检测门限获取方法∗

(电子科技大学电子工程学院,四川成都611731)

0 引言

杂波是制约雷达检测性能提升的重要因素,随着雷达探测威力的提升,探测环境的日益复杂化(时变空变性),杂波的统计特性越来越复杂,导致假设的杂波分布模型与实际杂波分布模型失配或者难以得到杂波的统计分布特性,此时,由先验信息假设背景杂波的统计模型[1-4],进行参数估计得到检测门限的传统CFAR检测方法将会导致严重的性能损失:实际虚警概率偏离期望值,检测概率下降。

针对模型失配导致性能下降的问题,一些适用范围更广的杂波分布模型被提出,文献[5-6]讨论了广义复合杂波分布模型,其分布函数一般是积分形式或无穷级数形式,只有在特殊参数取值下才有解析表达式。文献[7]针对海杂波时频域杂波模型与实际模型失配的情况,通过分析相参雷达时频域恒虚警(CFAR)检测门限与虚警概率的函数关系,提出一种基于最小二乘拟合的检测门限获取方法。文献[8-9]采用Alpha-Stable分布,但是其概率密度函数不存在解析表达式,仅能由特征函数来表达。事实上,不管设计的杂波模型多么复杂,均不能完整描述实际杂波统计特性,任何一种模型假设都是有偏差的[10]。

针对未知杂波背景中的目标检测问题,非参量CFAR检测器已经得到相应的研究。常用的非参量CFAR检测器主要包括两类:单样本非参量检测器和两样本非参量检测器。它们可以在不知道杂波分布模型的情况下实现检测。文献[11]介绍了符号检测器和Wilcoxon检测器两种单样本非参量检测器,它们能够在未知杂波分布模型下实现雷达目标的有效检测,但是在单次扫描条件下的虚警概率很高,需要进行多次扫描积累来降低虚警概率,这在一定程度上限制了该类CFAR检测器的应用,所以相关研究较少。文献[12-13]介绍了 Mann-Whitney检测器、Savage检测器和修正的Savage检测器,它们都属于两样本非参量CFAR检测器,都是针对多脉冲发射雷达系统设计的。另外,在文献[14]中,赫尔曼·罗林针对杂波功率未知的情况,将杂波功率的估算过程与目标判定过程结合起来改善检测性能。

针对杂波背景未知的情况,本文提出了一种新的非模型化的门限计算方法。利用核密度估计这种非参数估计方法实时估计杂波背景的分布函数,根据分布函数与上分位点之间的关系,估计检测门限,进而实现CFAR检测。成功解决了由模型失配或杂波模型未知导致的虚警概率偏离期望值的问题,同时保持良好的检测性能。

1 传统CFAR检测

本部分简要介绍了传统CFAR检测的原理及其存在的缺陷,主要包括传统检测门限的获取存在的缺陷。

1.1 信号检测模型

在实际的环境中,雷达回波信号是十分复杂的,不仅包含目标信号,而且还有各种杂波、接收机内部噪声等。由于噪声对雷达目标的检测影响不大,所以这里我们忽略噪声的影响。假设s(t)为目标回波信号,c(t)为杂波信号。从统计假设检验角度来看,信号检测问题就是在空假设H0和备选假设H1中作出判决。

上述回波信号都是在统计意义上描述的,为了判断哪个假设成立,我们需要知道两种假设下回波信号x(t)的概率密度函数(PDF),在雷达目标检测中,虚警概率Pfa和检测概率Pd的定义为

式中,p(x|H0),p(x|H1)分别为目标不存在和目标存在条件下回波信号幅度的PDF,T为检测门限。

CFAR检测是一种在奈曼-皮尔逊(NP)准则下从两种假设中挑选出最优假设的检测方法。CFAR检测器为了维持恒定的虚警性能,检测门限的设置必须能够自适应于杂波功率的变化。传统的参量检测器即是在给定杂波分布模型下,利用参考单元数据实时的估计杂波的分布参数,从而确定杂波的PDF,再由式(2)求得检测门限T,最后比较检测统计量和门限T的大小,输出点迹。

1.2 传统检测器的缺陷

1.2.1 模型失配

传统参量检测器要求杂波背景的统计特性已知,检测门限获取与杂波的统计分布特性密切相关,因此检测器设计的一个核心问题是雷达背景杂波统计特性的准确描述。当所选分布模型与实际杂波分布模型不符合,即模型失配时,将会导致传统检测器性能急剧恶化,检测器失去恒虚警特性,虚警点大幅度增多[15]。而杂波分布特性与雷达入射角、极化方式、地形分布、人造建筑和预处理方式(相参积累、幅度检波等)等条件密切相关。上述任何一个条件发生变化,杂波的统计特性都有可能随之改变,最终导致传统检测器性能恶化,下面我们用具体例子分析其性能恶化程度。

假设根据先验知识判定杂波幅度服从瑞利分布,实际上服从Log-normal分布,相应的PDF分别为

式中,σ1为瑞利分布的参数,μ和σ2分别为Log-normal分布的尺度参数和形状参数。

设参考单元矢量为X,令Y=ln(X),采用适合于瑞利分布的CA-CFAR检测器,在先验瑞利分布下设定检测器的虚警概率为Pf,实际得到的虚警概率为P′f。我们可以得到瑞利分布模型下Pf与检测统计量Y的门限T Y的理论关系为

实际上参考单元服从参数为(μ,σ)Log-normal分布,对数变换后服从高斯分布,所以实际得到的虚警概率为

图1为Pf和P′f的对比曲线,可以看出在相同的T Y下两者之间的差别很大,例如当设定虚警概率为10-4时,实际的虚警概率为1.59×10-1,相差3个数量级。而且随着设定虚警概率的减小,相差越来越大,实际的虚警值偏离设定值,检测器失去恒虚警特性。

图1 模型失配带来的虚警概率损失

1.2.2 杂波背景未知

针对杂波背景未知的雷达探测问题,传统的参量CFAR检测器失去恒虚警能力。此时,我们通常采用非参量CFAR检测方法,现有的非参量检测只有单样本和双样本非参量检测方法两种。单样本非参量检测采用在单次脉冲扫描中检测单元信号与参考杂波样本的比较结果实施检测。在单次扫描下的虚警概率很高,需要进行多次扫描积累来降低虚警概率,这在一定程度上限制了该类CFAR检测器的应用,图2(a)给出了单样本检测在不同虚警概率下的检测结果。由图2(a)可知,在虚警概率Pfa≤10-2时,检测概率为0,即能够正确检测目标所需求的虚警概率为Pfa=10-1,虚警概率太高,不符合实际雷达系统的要求。双样本检测采用检测单元信号在所有脉冲扫描中与参考杂波样本的比较结果实施检测。有效解决了单样本检测虚警概率过高的问题。但是其检测性能受脉冲积累个数的影响很大,在脉冲个数较少的情况下,检测性能不佳。图2(b)给出了在虚警概率Pfa=10-3时,不同脉冲积累数下的检测结果。由图2(b)可知,随着脉冲累积数的减少,检测概率下降较快。

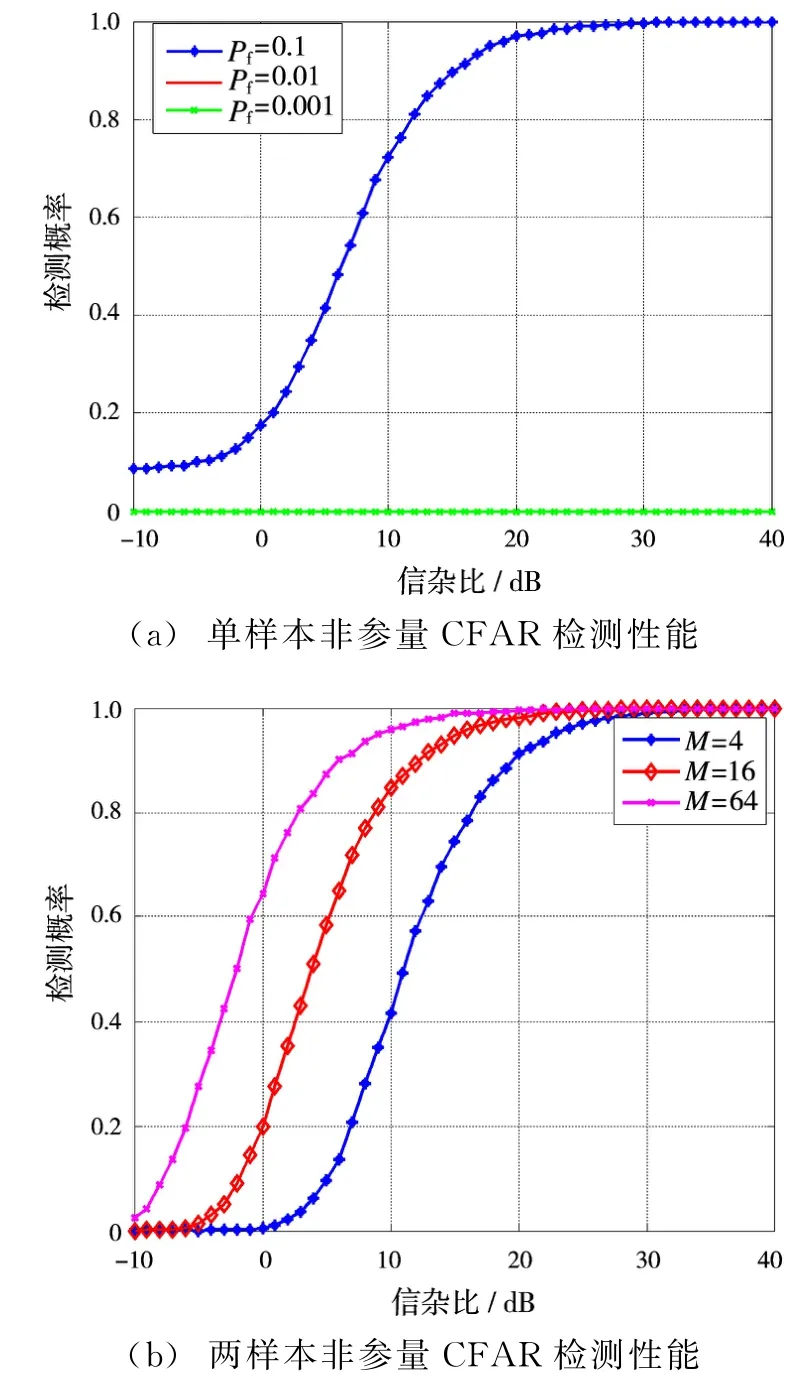
图2 非参量CFAR性能分析

本文针对杂波模型失配及杂波统计特性未知情况,综合提出了一种新的CFAR检测方法,该方法成功解决了由杂波分布特性未知引起的虚警概率偏离期望值,以及单次扫描情况下非参量CFAR检测器检测性能严重下降的问题。在保持恒定虚警概率的情况下获得了良好的检测性能。

2 改进方案

前面提到过检测门限的获取与杂波的统计分布特性密切相关,所以在未知杂波背景下,如何准确地获取杂波分布函数就成为了解决本文难题的关键。针对此问题,本文采用核密度估计方法来准确估计杂波的分布函数,确定检测门限。下面我们分三个方面来详细介绍其工作原理。

2.1 改进检测器结构

改进检测器的基本原理是利用核密度估计方法处理参考单元内的杂波数据,实时地估计杂波的分布函数,进而确定检测门限,实现CFAR检测。其基本结构如图3所示,其中N为参考窗长度,x i(i=1,2,…,N)为参考单元杂波数据。与传统的CFAR检测器相比,提出的检测器同样利用了CUT附近的参考单元数据,但其对杂波数据的处理是为了获得杂波分布函数的估计,不是为了获得杂波分布函数的参数估计。对于实际系统中的各种未知杂波,其分布函数均可采用核密度估计的非参量估计方法实现。因此,改进的检测器能够解决杂波分布特性未知引起的检测性能损失问题。

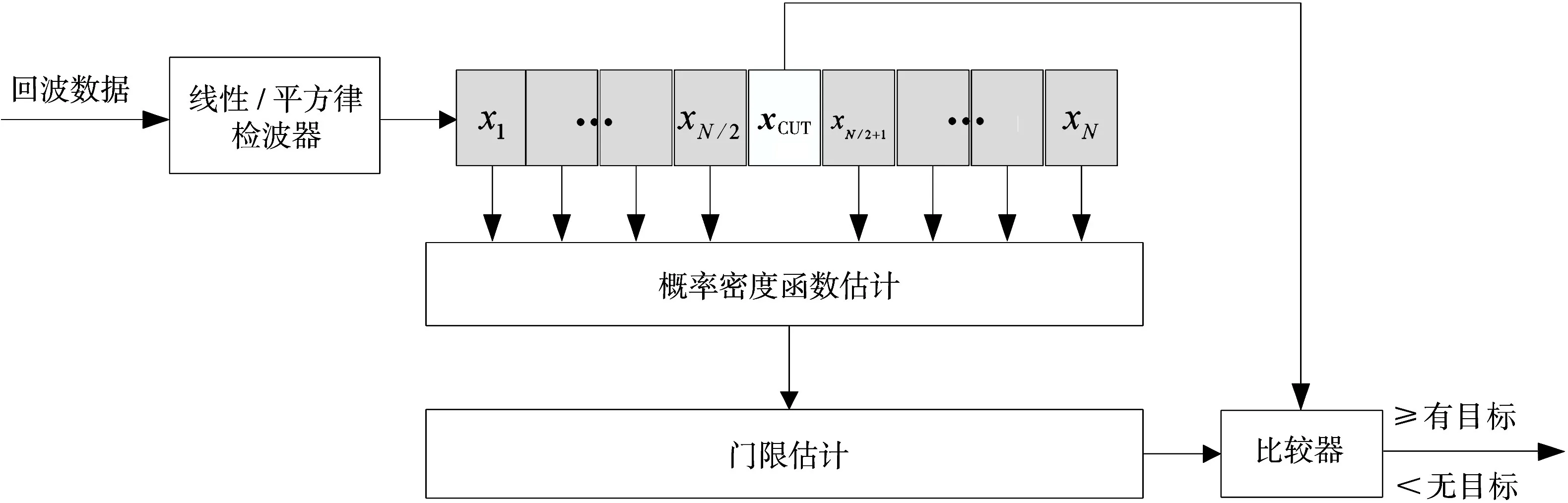
图3 K-CFAR检测器框图

2.2 杂波分布函数估计

未知杂波背景中的检测难点是杂波分布函数的获取,为了解决这个问题,我们利用核密度估计方法[16]实时地估计杂波分布函数。核密度估计是概率密度非参数估计的一种,其基本思想是:选定某一种核函数,对于每一点x,待估计的概率密度函数(x)是以x为中心的核函数的平均。下面给出核密度估计的定义:给定一个核函数K和一个称为带宽的正数h,核密度估计定义为

这里我们采用高斯核,其数学表达式为式(9),且带宽是影响估计精度的一个重要因素,它的大小由式(10)确定,其中,K∗(x)=K2(x)-2K(x)。

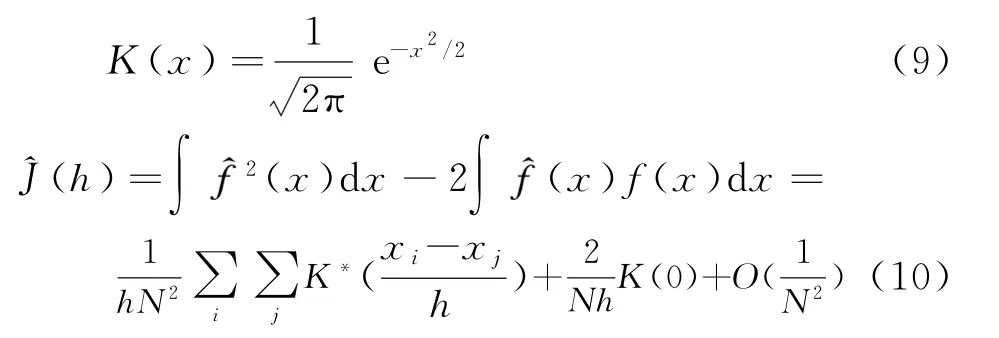
对估计得到的概率密度函数取积分,经过积分运算,最终得到分布函数的解析表达式为

2.3 检测门限估计

由估计得到的分布函数表达式(11),根据分布函数与上分位点之间的关系,可以得到检测门限的表达式为

式中,Pfa为虚警概率的逆函数。

结合式(2)和式(12),我们可以得到虚警概率与检测门限之间的数学表达式为

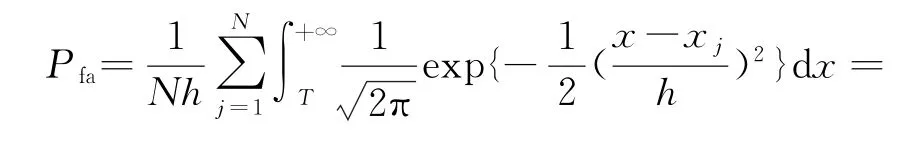
利用2.2和2.3节的研究,我们利用核密度估计准确地估计杂波的分布函数,在给定虚警概率下,确定检测门限,成功解决了未知杂波背景下雷达目标的恒虚警检测问题。

3 性能分析

3.1 核密度估计仿真验证

我们通过比较广义概率密度函数(GPDF)和估计得到的概率密度函数的误差来验证核密度估计的准确性。图4(a)、(c)分别给出了Log-normal分布、Weibull分布下的概率密度函数对比结果。图4(b)、(d)是估计与真实概率密度函数之间的误差。误差e=|f-f′|是绝对误差。

根据图4可知,概率密度函数右截尾的估计误差都在0.1以下,而检测门限的准确确定正是由概率密度函数右截尾确定的,所以概率密度函数右截尾的高估计精度可以满足检测门限估计的精度要求。

3.2 虚警特性分析

假定杂波服从Weibull分布,在不同检测门限下,分析K-CFAR检测器的虚警概率随分布参数(形状参数、尺度参数)的变化情况,仿真结果如图5所示。

根据图5可知,基于核密度估计的CFAR检测器,在不同的尺度参数下,其虚警概率与Weibull分布下最优CFAR检测器的虚警概率相差无几;在不同的形状参数下,随着形状参数的增大其虚警概率偏大于最优检测器下的虚警概率,但是在可容许的误差范围内,对检测结果没有太大的影响。所以K-CFAR具有与传统最优CFAR相同的恒虚警特性。

3.3 检测性能分析

假定杂波分别服从Weibull分布,雷达目标为SwerlingⅠ起伏模型,具有归一化的,在(-π,π]内均匀分布的随机多普勒频移。虚警概率Pfa=10-4,CFAR窗长度N=8或32,蒙特卡洛次数为10000次。我们采用Weibull分布下的WLH-CFAR检测器作为比较对象。图6给出了Weibull分布背景下最优CFAR检测器(WLH-CFAR)和本文提出的K-CFAR检测器的检测性能曲线对比。

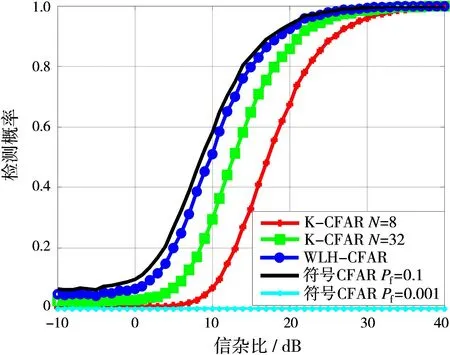
图6 Weibull分布背景下WLH-CFAR和K-CFAR的检测性能曲线对比

根据图6的结果可知,随着参数N的增多,K-CFAR检测器的检测性能越来越接近最优CFAR检测器。由此可知,对于大的N值,K-CFAR检测器具有与最优CFAR检测器相同的渐近检测功效。

综合图5、图6可知,在未知杂波背景下,KCFAR检测器不仅具有恒虚警特性,同时具有渐近与最优CFAR检测器的检测性能,且在相同虚警概率下优于非参量的符号CFAR检测器。KCFAR检测器具有对各种已知或未知杂波背景的适应性,其检测器具有通用性,优于针对特定杂波背景的参量CFAR检测器。

由上述所有仿真验证可知,在给定虚警概率下,K-CFAR检测器可达到与传统参量CFAR检测器相同的检测性能。此外,K-CFAR检测器具有对各种未知杂波的适应性,检测器具有通用性。而传统的参量CFAR检测器只在特定杂波分布模型下具有最优的检测性能,因此,从通用性角度看来,K-CFAR检测器优于传统的参量CFAR检测器。

4 结束语

本文针对未知杂波背景下的雷达目标检测问题,提出了一种新的CFAR检测器K-CFAR。KCFAR检测器主要利用核密度估计的非参数估计方法实时估计杂波分布特性,根据分布函数和虚警概率的关系求取检测自适应门限。仿真数据验证表明,K-CFAR检测器可达到与常规的参量CFAR检测器相同的检测性能,对杂波背景具有自适应性,且具有通用性强的特点。

上述检测器在均匀的未知背景下具有良好的性能,为了增强K-CFAR检测器的实用性,我们需要研究非均匀未知背景、多目标等情形下的适应性。这将是我们下一步的研究重点。

[1]SARMA A,TUSTS D W.Rank-Order Adaptive CFAR:Performance Bounds and Efficient Implementation[J].IEEE Trans on Aerospace and Electronic Systems,2013,49(4):2211-2224.

[2]HEZARKHANI A,KASHANINIA A.Performance Analysis of a CA-CFAR Detector in the Interfering Target and Homogeneous Background[C]∥International Conference on ICECC,[S.l.]:[s.n.],2011:1568-1572.

[3]CAO T V.Constant False-Alarm Rate Algorithm Based on Test Cell Information[J].IET Radar,Sonar&Navigation,2008,2(3):200-213.

[4]DE FIGUEIREDO F A P,MIRANDA J P C L,CARDOSO F A C M,et al.A Modified CA-CFAR Method for LTE Random Access Detection[C]∥International Conference on ICSPCS,Carrara,VIC:IEEE,2013:1-6.

[5]NITZBERG R.Contant-False-Alarm-Rate Signal Processors for Several Types of Interference[J].IEEE Trans on Aerospace and Electronic Systems,1972,8(1):27-34.

[6]FARINA A,GINI F,GRECO M V,et al.High Resolution Sea Clutter Data:Statistical Analysis of Recorded Live Data[J].IET Radar,Sonar&Navigation,1997,144(3):121-130.

[7]陈建军,黄孟俊,赵宏钟,等.相参雷达时频域CFAR检测门限获取方法研究[J].电子学报,2013,41(8):1634-1639.

[8]ROY L P,KUMAR R V R.Accurate K-Distributed Clutter Model for Scanning Radar Application[J].IET Radar,Sonar&Navigation,2010,4(2):158-169.

[9]石志广,周剑雄,付强.K分布海杂波参数估计方法研究[J].信号处理,2007,23(3):420-424.

[10]ANASTASSOPOULOS V,LAMPROPOULOS G A,DROSOPOULOS A,et al.High Resolution Radar Clutter Statistics[J].IEEE Trans on Aerospace and Electronic Systems,1999,35(1):43-59.

[11]CHEN H,VARSHNEY P K,KAY S,et al.Noise Enhanced Nonparametric Detection[J].IEEE Trans on Information Theory,2009,55(2):499-506.

[12]AL-HUSSAINI E K,TURNER L F.The Asymptotic Performance of Two-Sample Nonparametric Detectors When Detecting Nonfluctuating Signals in Non-Gaussian Noise[J].IEEE Trans on Information Theory,1979,25(1):124-127.

[13]YILMAZ K,UNER M.Non-Parametric Radar Detection in Homogeneous and Non-Homogeneous Environments[C]∥Signal Processing and Communications Application,Eskisehir:IEEE,2007:1-4.

[14]赫尔曼·罗林.有序统计恒虚警率技术综述[J].雷达科学与技术,2012,10(2):117-123.

[15]冉世领,赵宏钟,付强.基于局部累积概率密度函数估计的CFAR检测门限获取新方法[J].信号处理,2012,28(12):1692-1699.

[16]WASSERMAN L.现代非参数统计[M].吴喜之,译.北京:科学出版社,2008.