基于随机积分的非线性滤波跟踪算法∗
(电子科技大学电子工程学院,四川成都611731)
0 引言
雷达系统中常会遇到非线性状态估计问题,例如目标再入问题[1],目标运动复杂,其状态方程是非线性函数;或混合坐标系下目标跟踪,其量测方程是非线性函数等[2]。解决非线性状态估计问题,贝叶斯滤波结构为系统状态估计提供了一种递归结构。与线性系统直接利用卡尔曼滤波递归求得最优解不同[3],在贝叶斯滤波结构下很难对非线性系统实现递归求解。只有获得了系统状态的后验概率分布的完整描述才能获得非线性状态估计问题的最优解[4],然而很少情况下能精确描述后验概率。
因此,人们提出了大量的次优滤波算法,EKF滤波算法是解决非线性滤波的最常用的方法[5],该算法通过对非线性函数一阶泰勒级数展开将非线性问题转化为线性问题,但在线性化过程中引入了模型误差,而且需要计算Jacobian矩阵,增大了计算量,也容易出现滤波发散问题,因此在实际应用中受到了很大的限制。随后Julier等人提出一种不敏卡尔曼滤波(UKF)算法[6-7]。UKF对状态向量的PDF进行近似化,表现为选取一系列的采样点通过非线性函数传播,捕获非线性函数的统计特性,得到后验均值和协方差精确达到2阶。UKF在模型参数估计、目标跟踪等方面都得到了较广泛的应用,但是当状态维数增加或系统非线性强时,UKF滤波会出现精度急剧下甚至发散等问题。2009年,加拿大学者Arasaratnam提出一种新的贝叶斯近似滤波算法——容积卡尔曼滤波算法(CKF)[8],该算法为非线性估计问题提出了一种新的实现方式,CKF应用球面径向容积准则对函数积分进行近似,解决了贝叶斯滤波结构下积分问题。近年来,CKF已经应用到了非线性滤波估计上,例如目标跟踪和数据融合[9-10]。该算法在一定程度上克服了EKF和UKF在强非线性系统中的应用局限性,但是随着模型状态维数的增加或系统非线性增强时,CKF的跟踪性能下降。
针对存在的问题,本文提出一种新的非线性滤波跟踪算法——随机球面径向积分滤波算法(SSIF)。该算法利用随机球面径向准则近似积分方程来实现滤波递归,首先利用随机球面积分规则近似球面积分,再利用随机径向积分规则近似径向积分。通过该方法可以消除系统误差提升系统的跟踪精度和滤波稳定度,具有更快的收敛速度和更优的数值逼近能力。通过蒙特卡洛仿真实验表明,利用本文提出的非线性滤波算法对雷达系统的非线性目标跟踪整体性能有明显提升。
1 系统描述和问题
考虑非线性离散随机系统[2,6]
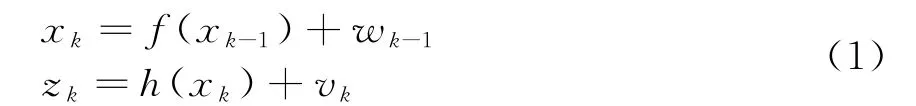
式中,状态x k∈ℝn,n表示状态维数;z k∈ℝm,m表示量测维数;w k,v k分别是相互独立的过程噪声和观测噪声,满足均值为0、协方差分别为Q k,R k的高斯分布。
假设在k-1时刻状态后验概率函数为p(x k-1|z1:k-1),则预测状态的概率密度函数p(x k|z1:k-1)可表示为

根据所接收到的量测z k,更新后验概率

式中,p(z k|x k)为似然函数。
假设状态预测概率密度函数p(x k|z1:k-1)和似然函数p(z k|x k)均为高斯函数,因此后验概率密度函数p(x k|z1:k)仍是高斯函数,确定该密度函数只需要计算这些高斯概率密度函数的均值和方程即可。对于式(1)所描述的系统,贝叶斯结构滤波器可概括为两步:预测和更新[8]。
(1)预测
第1步:初始化,在时间k=0时,定义先验概率p(x0|z-1)=p(x0),相应的均值和方差分别为
第2步:计算状态均值x k|k-1和方差p k|k-1

式中,D k-1表示过去输入的量测数据。
将式(4)代入式(1),则有

由于w k是0均值不相关的高斯白噪声,因此有
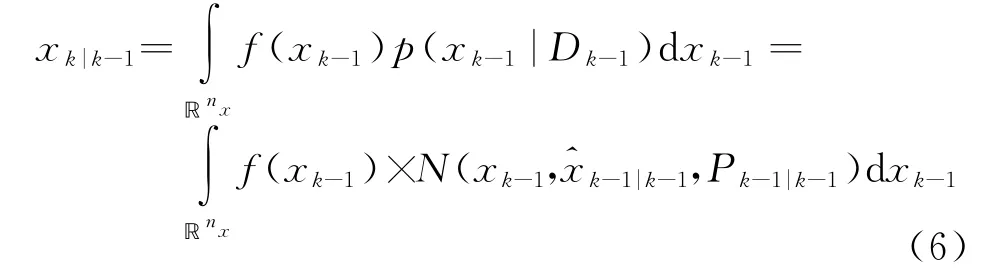
相应的误差协方差
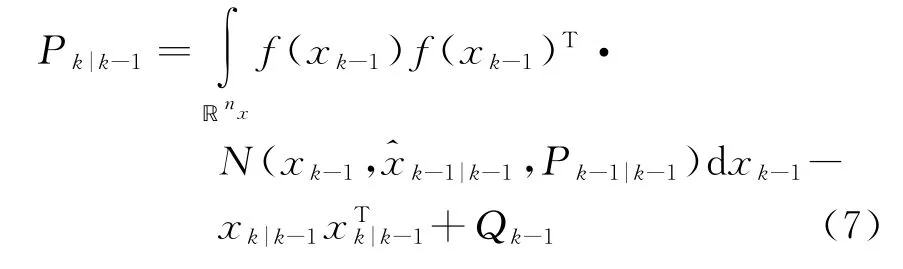
(2)更新

式中,

根据上述贝叶斯滤波结构,可以发现问题关键在于计算多维函数积分,被积函数的形式为非线性函数乘以高斯概率函数[11]。实现对多维函数积分难度较大,因此需要有效的数值积分对其近似。近年来涌现了大量的对该积分近似的方法,如EKF,UKF和CKF等,由于这些方法存在精度差和容易发散等问题。因此本文提出一种更为有效的积分近似算法,该算法利用随机球面积分规则和随机径向积分规则近似积分函数来实现滤波递归。
2 随机球面径向积分滤波器(SSIF)
在高斯背景假设下,贝叶斯滤波结构下函数的积分形式都可表示为

式中,f(·)表示任意函数。
很难解决式(11)的积分,因此需要找出一种方法近似该积分。一种数值积分近似的方法是通过找到一组权值w i和采样点x i,利用权值和被积函数的加权可近似该积分函数:
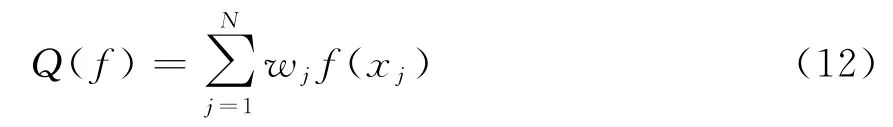
式中,N表示采样点总数。
利用球面径向变换规则对式(11)进行变换,利用x=ry替换,且yTy=1,r=x xT,因此式(11)表示为

式中,U n={y∈ℝn|yTy=1},式(13)可分解为

因此对式(11)的积分近似转化为对式(14)的积分进行近似。
(1)随机球面积分规则
对球面积分选择适合的积分准则,通过旋转随机积分准则,将所得到的值加权来近似球面积分[12-13]
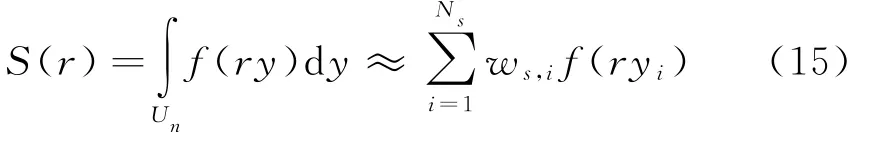
其中,对于所有的i有
作为一个球面积分近似规则,在单位球面U n上近似积分函数f(y),且yTy=1;假设Q是n×n的正交矩阵,则

由于‖Qy‖=‖y‖,所以式(16)同样是对球面U n的一个积分规则,如果式(15)是3阶函数,则式(16)同样是一个3阶函数,假如Q是服从均匀分布,则S Q为球面U n的无偏积分规则。
因此,在3阶随机积分规则下,式(16)可近似为

(2)随机径向积分规则
通过下面的公式来近似估计N r点的径向积分[12]:

给定点{r i}和权值{w i}就可以确定该积分,点{r i}随机选取以保证式(19)的无偏性,设置r0=0,点集的联合概率密度函数p(r1,r2,r3,…,r n)如式(20)所示。
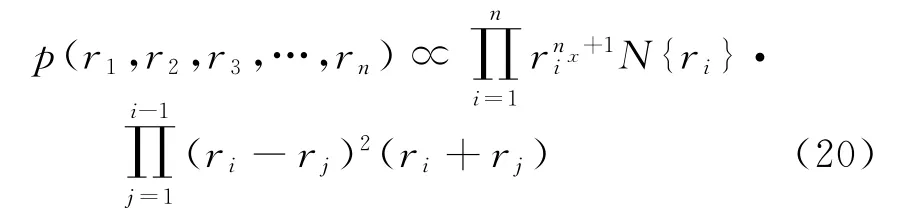

则函数积分I(f)用3阶随机径向积分近似为
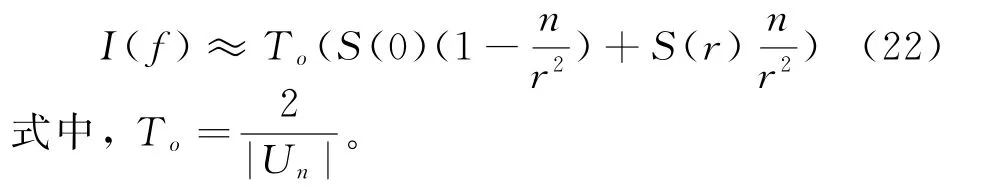
(3)随机球面径向积分规则
将随机球面规则和随机径向规则联合起来成为一种近似I(f)的简单随机积分规则——随机球面径向积分规则。本文提出的新积分规则能有效近似函数积分,且保证估计的无偏性。函数的积分可近似为SR Q,r(f),具体形式为


因此,跟踪3阶随机球面径向积分规则:

具体的3阶随机球面径向规则积分算法[13]如下:
第1步 设置误差容忍度ε,最大迭代次数Nmax,采样点数n。
第2步 设置迭代次数N=0,初始积分值I=,初始化积分均方误差,估计均方误差S x,且,计算F0=f(0)。
第3步 重复迭代
(a)设置N=N+1,SR q,r=0;
(b)产生n x×n x维的均匀分布的随机正交矩阵Q;
(c)产生随机数r~Chi(m+2);
(d)从j=1,2,…,n x循环,SR q,r=SR q,r+
第4步 输出I(f)≈I,即I为积分公式I(f)的近似值。
(4)随机球面径向积分滤波器的设计
利用3阶随机球面径向积分规则算法来近似贝叶斯滤波器结构中的积分,形成一种简单的随机积分滤波器(SSIF)。状态预测式(6)~(7)利用式(26)计算,计算预测状态x k+1|k时,p(x)和f(x)分别用p(x k|z k)和f(x k)代替;计算预测状态协方差矩阵P k+1|k时,利用f(x k)f(x k)T代替f(x)。同理,可以估计式(10)。
SSIF滤波跟踪算法步骤如下:
第1步 设置时间k=0,参数Nmax,误差容忍度ε,采样点数n,初始化状态均值和协方差矩阵分别为x0|0=E(x0)=x0,p0|0=E(p0)=p0。
第2步 状态预测

第3步 量测更新


完成更新,令k=k+1,继续步骤2。
3 仿真实验及分析
本文所提的非线性滤波算法与不敏卡尔曼滤波算法(UKF)和改进的容积卡尔曼滤波算法(SCKF)在非线性跟踪系统中进行比较,并对结果进行分析。假设目标匀加速机动飞行,目标状态为(在 三 维 空 间 中它包含了目标各个方向的位置、速度和加速度,因此n x=9)。直角坐标系下状态方程为

式中,w k表示均值为零的高斯白噪声,协方差矩阵所以Q=q s·diag(Q1,Q1,Q1),q s为功率谱密度,且Q1为
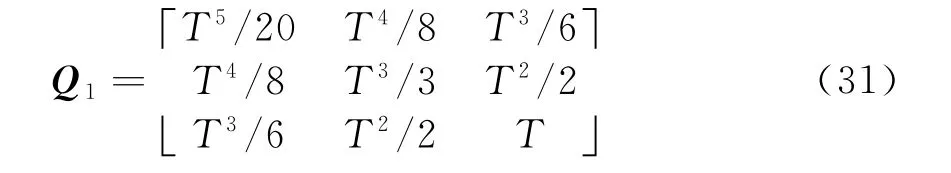
F ca=diag[I3⊗F],T表示采样时间间隔,I3表示3×3的单位阵,⊗表示Kronecker乘法。
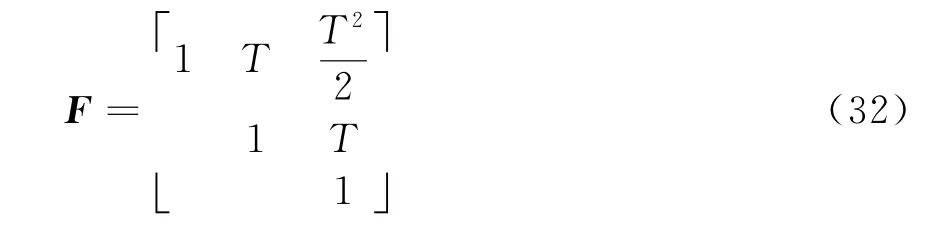
雷达观察到的目标量测为极坐标系下数据,因此第k时刻的量测z k为

式中,v k为零均值的高斯白噪声,其协方差矩阵,且非线性量测方程h(x k)为

假设目标在0~25 s内一直作匀加速运动,雷达位于坐标原点位置,目标初始位置为[x,y,z]=[8 km,9 km,1 km]T,速 度 为150 m/s,150 m/s],加 速 度 为6 m/s2,15 m/s2],采样时间间隔T=0.5 s,总跟踪时间t=25s,距离均方根误差δr=10 m,俯仰角和方位角均方根误差分别为δθ=δφ=2°,功率谱密度q s=0.1 m2·s-1,最大迭代次数Nmax=50,误差容忍度ε=0.5,进行500次蒙特卡洛仿真实验,位置的均方根误差定义为

式中,x,y,z为目标真实坐标位置为目标估计位置,M为蒙特卡洛仿真实验次数。
图1为匀加速机动目标运动轨迹,通过蒙特卡洛仿真实验,得到目标跟踪的位置均方根误差曲线图(图2)、速度均方根误差曲线图(图3)、加速度均方根误差曲线图(图4)和不同参数下新算法对目标的跟踪性能(表1)。仿真中分别利用UKF和CKF滤波算法以及本文提出的非线性滤波算法对非线性雷达系统进行跟踪估计,从图2、图3和图4可以看出,本文所提的非线性滤波算法具有更高的跟踪精度,对目标加速度、速度和位置的估计更为精确,稳定性更强,使跟踪的整体跟踪性能得到一定提升。从表1可以得出,随着迭代次数N的增加或误差容忍度ε的减小,新算法的性能有进一步的提高,位置和速度的均方根误差都有一定的提升。但由于迭代次数N增加,计算量相应的会增加,因此需要综合考虑计算量和性能,N的取值不宜过大。

表1 不同参数下跟踪结果

图1 目标运动轨迹图

图2 位置均方根误差曲线图

图3 速度均方根误差曲线图
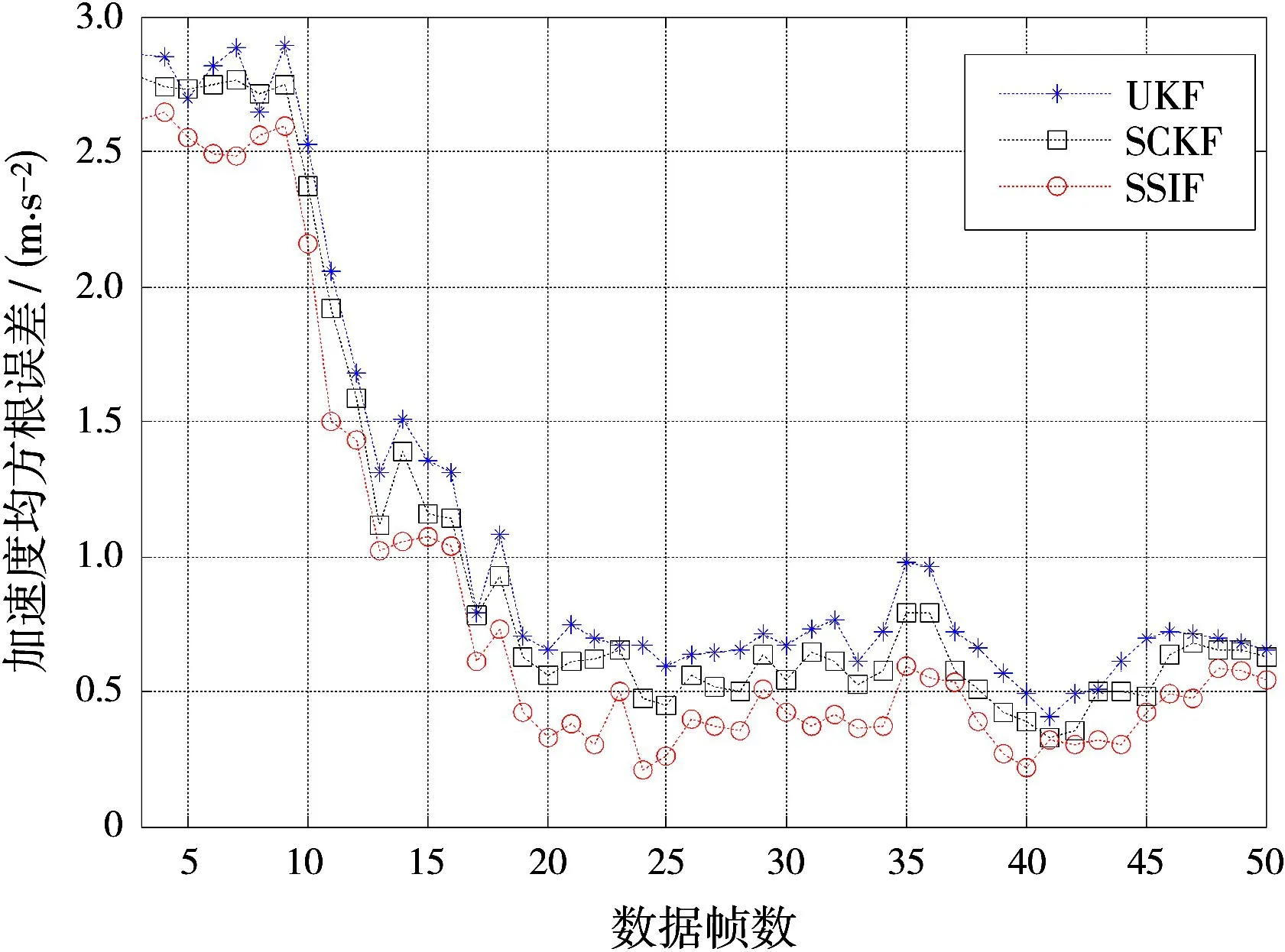
图4 加速度均方根误差曲线图
4 结束语
本文主要提出一种新的非线性滤波算法——随机球面径向积分滤波算法(SSIF),该算法基于随机积分规则,即利用随机球面积分规则和随机径向积分规则实现对贝叶斯结构下函数积分的近似。对雷达系统的非线性目标跟踪中,相较于传统的非线性滤波跟踪算法,本文提出的滤波算法消除了系统误差,提高了跟踪精度,且有效地抑制了非线性滤波易出现发散的问题,提升了跟踪的稳定性。通过蒙特卡洛仿真实验证明,该算法对非线性目标跟踪性能有明显的提升。
[1]STRAKA O,DUNIK J,SIMANDL M.Randomized Unscented Kalman Filter in Target Tracking[C]∥Proceedings of the 15th International Conference on Information Fusion,Singapore:[s.n.],2012:503-510.
[2]GARCÍA-FERNÁNDEZ A F,MORELANDE M R,GRAJAL J.Nonlinear Filtering Update Phase via the Single Point Truncated Unscented Kalman Filter[C]∥2011 Proceedings of the 14th International Conference on Information Fusion,Chicago,IL:IEEE,2011:1-8.
[3]金亮亮,刘亚云.一种改进自适应机动目标跟踪算法[J].雷达科学与技术,2014,12(1):97-100.
[4]NØRGAARD M,POULSEN N K,RAVN O.New Developments in State Estimation for Nonlinear Systems[J].Automatica,2000,36(11):1627-1638.
[5]GUSTAFSSON F,HENDEBY G.Some Relations Between Extended and Unscented Kalman Filters[J].IEEE Trans on Signal Processing,2012,60(2):545-555.
[6]JULIER S J,UHLMANN J K.Unscented Filtering and Nonlinear Estimation[J].Proceedings of the IEEE,2004,92(3):401-422.
[7]刘妹琴,汤晓芳,郑世友,等.基于RUKF-IMM的非线性系统滤波[J].华中科技大学学报,2013,41(5):57-63.
[8]ARASARATNAM I,HAYKIN S.Cubature Kalman Filters[J].IEEE Trans on Automatic Control,2009,54(6):1254-1269.
[9]DAHMANNI Mohammed,MECHE Abdelkrim,KECHE Mokhtar.Reduced Cubature Kalman Filtering Applied to Target Tracking[C]∥2ndInternational Conference on Control,Instrumentation and Automation,[S.l.]:[s.n.],2011:1097-1101.
[10]霍光,李冬海,李晶.机动目标单站无源定位中的量测更新CKF-IMM算法[J].电子信息对抗技术,2013,28(5):33-38.
[11]ARASARATNAM I,HAYKIN S,ELLIOTT R J.Discrete-Time Nonlinear Filtering Algorithms Using Gauss-Hermite Quadrature[J].Proceedings of the IEEE,2007,95(5):953-977.
[12]STROUD A H.Approximate Calculation of Multiple Integrals[M].NJ:Prentice-Hall,1971.
[13]GENZ A,MONAHAN J.Stochastic Integration Rules for Infinite Regions[J].SIAM Journal on Scientific Computation,1998,19(2):426-439.

