机载斜视SAR图像的定位方法∗
(中国电子科技集团公司第三十八研究所,安徽合肥230088)
0 引言
SAR图像中地面目标的定位,就是对其合成孔径图像的相应像元定位。在实际应用中主要采用根据像素和参考点相对位置关系来确定目标的位置[1],通常情况下机载作用距离较短,这种方法并不考虑地球曲率弯曲影响,但是随着雷达技术的发展,机载SAR作用距离越来越远,如果还是使用相对位置方法对目标进行定位,就必须考虑地球曲率的影响,在星载图像定位中,主要采用斜距多普勒模型,该方法需要对三元方程组进行求解,求解困难,因此本文提出了一种适用于机载图像的定位方法。另外,在大斜视成像过程中,方位压缩不同导致了目标相对位置在图像上的变化,从而会影响目标定位的计算。本文针对机载斜视SAR大作用距离下的图像定位提出了一种计算方法,并对此方法进行了试验研究。
1 算法概述
假设飞行器到地球的垂线的反向延长线经过地心,如图1所示,R z为飞行器在地球上的投影点处与地心的距离,R a为照射点A在地球上的投影点与地心的距离,h z为飞行器的高度,h a为照射点的高度。飞行器的经纬度可以在惯导中提取,通过WGS-84坐标系下转换公式求出R z为
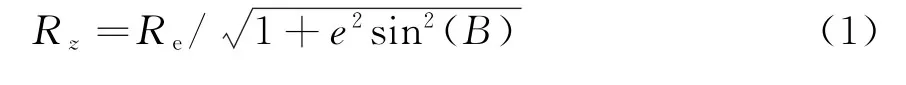
式中,Re为地球长半轴,e为第一偏心率,B为飞行器的纬度。
由于求A点的经纬度,R a未知,在求解时首先将R a设为R a=R z。h a是根据成像区域平均海拔高度给出。根据余弦定理求出p h为
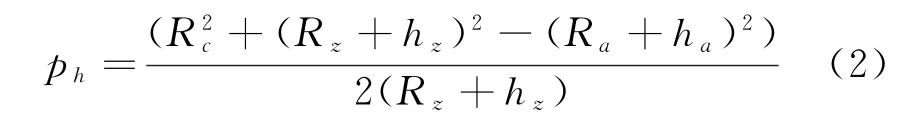
如果想要求A点的经纬度,那么可以先求出A点在东北天坐标系下的坐标,如图2所示,其中XYZ是以图1中o′为原点的东北天坐标系,X′Y′Z为飞行坐标系。A点在飞行坐标系下的坐标可以求得:

式中,θ为斜视角。
那么A点在东北天坐标系下的坐标为

式中,α为航向角。

图1 目标与飞行器的相对位置在地球上的显示

图2 东北天坐标系与飞行坐标系
根据东北天转换成地心坐标系下的坐标,假设东北天坐标系下某一点坐标为(x a,y a,z a),向地心坐标的转换公式为
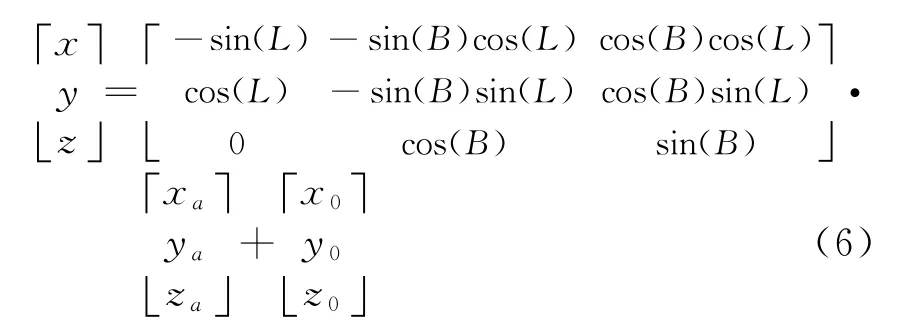
式中,(x0,y0,z0)为东北天坐标系原点在地心坐标的坐标系,B和L为东北天坐标系原点的经纬度。
通过计算大地坐标的简便公式[2]对A点经纬度进行计算,计算公式如下:

式中,Re,R p为长短半轴,e,e′为第一、第二偏心率。根据WGS-84坐标系规定,Re=6 378 137.0,R p=6 356 752.314 20.006 739 496 78。得到的A点位置信息为(B a,L a,H a),此时完成对A目标点的定位。
另外,在图像定位时一般是对图像的4个顶点进行定位,而4个顶点分别对应的飞行器的位置需要通过不同斜视角情况下进行讨论。在正侧视时,飞行轨迹和所成图像的关系如图3所示。

图3 正侧视飞行轨迹
如图3所示,正侧视飞行时,多普勒中心为0,图像位于飞行轨迹的正侧方,A、B两点对应的飞行器位置为O1,C、D两点对应的飞行位置为O2。但是假如SAR成像并不为正侧视而是斜视成像,当进行方位压缩时,需要对所成图像进行方位位移,将偏离中心位置的图像移动到图像的正确位置上来,如图4所示。
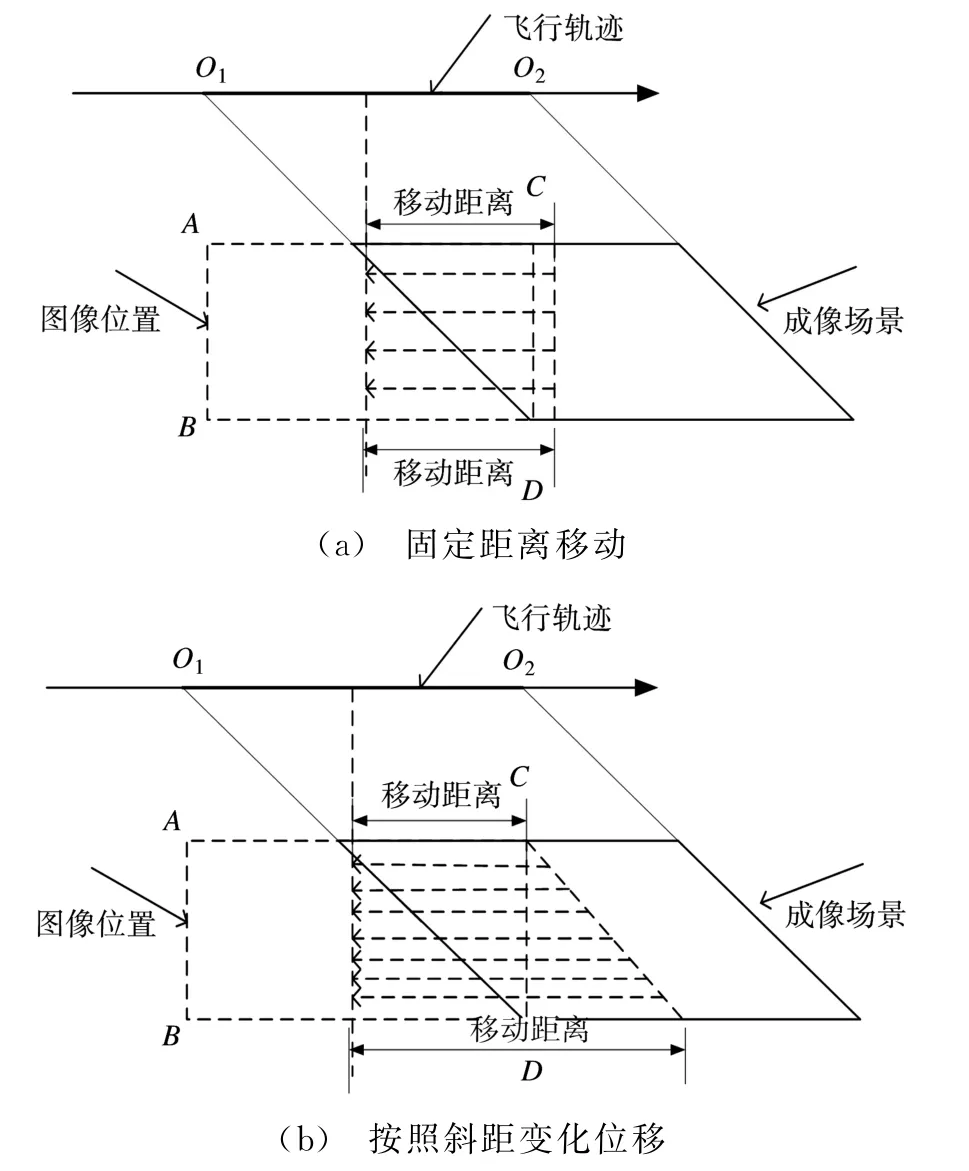
图4 方位压缩移动图像
在实时处理中,存在两种移动方式:一种是相同距离移动,另一种是按照斜距的变化进行移动。如图4所示,第二种移动方式是最好的,因为在第二种移动方式中,成像场景中的目标点都可以移动到图像位置上来,这样就保证了成像场景的完整性,这种移动方法A、B两点对应的飞行器位置为O1,C、D两点对应的飞行位置为O2。
在实际处理中,有时可能出于计算速率等原因,需要进行同距离移动,如图4(a)所示,这时A、B两点对应的飞行器位置并不是O1,C、D两点对应的飞行位置也不是O2。这时,需要进行几何分析,求出所要定位点在何时刻被波束中心照射,才能通过此时刻的飞行位置将目标位置求出。对于等距离移动的图像定位的分析如图5所示。
如图5所示,等距离移动方法是将图像A′B′C′D′移动到abcd,其中载机平台飞行到A点时,波束中心照射到A′,飞行到B点,波束中心照射到B′;飞行到C点,波束中心照射到C′,飞行到D点,波束中心照射到D′,而A′B′E和C′D′F由于位于abcd场景外,因此被舍去,这会使得图像变小,减小的点数为

图5 图像对应飞行器位置

在定位计算时,可以根据图5所示的几何关系找到对应的飞行点。如图6可以看出两种移动方式对所成图像的影响。
由图6可以明显地看出,在每条距离线上,目标分布根据方位压缩移动方式的不同而不同。因此在定位时需确定方位压缩方式,再根据图5的几何关系确定飞机参考点。

图6 不同位移方式成像结果对比图
2 实验与验证
我们通过仿真实验和外场试验分别对算法作出了验证。在仿真实验中,我们与星载定位经常采用的斜距 多普勒定位[3-4]方法进行精度和定位时间上的比较。假设载机位于东经60°,北纬45°,飞行高度为10 km,正北飞行,飞行速度为100 m/s。假设目标点与载机距离为200 km,斜视角为20°,地面高度为100 m。在不同作用距离下得到的结果如表1所示[5]。
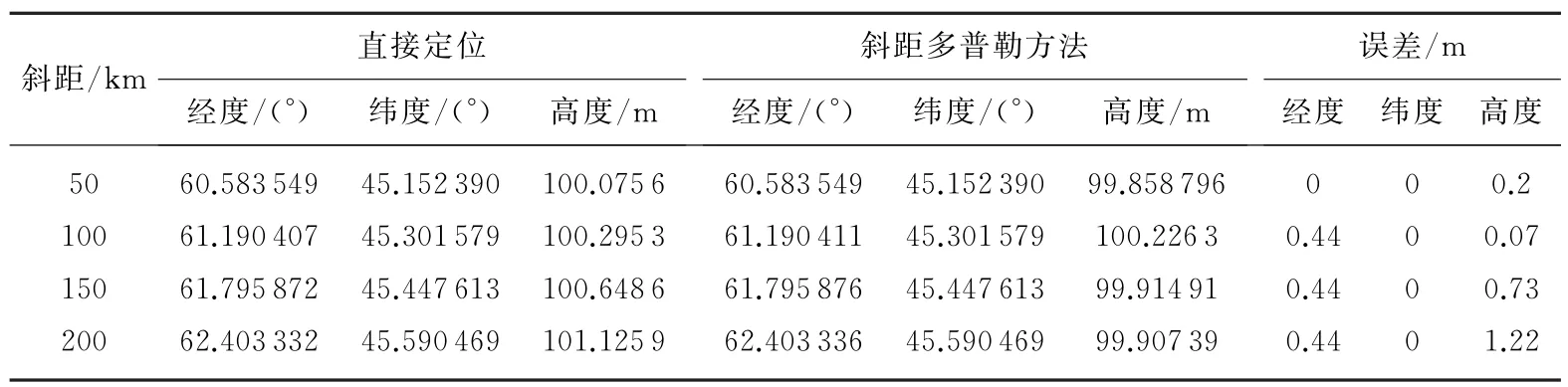
表1 不同雷达作用距离的定位仿真结果
由表1可以看出,本文提出的方法与星载SAR经常使用的距离多普勒定位方法结果基本一致,误差小于2 m,这符合定位精度要求。由于距离多普勒方程需要解算三元方程组进行定位,定位方法复杂,因此算法结构简单的直接定位方法更适用于远距实时机载定位。
以上我们采用的是理想的目标对定位的论证,为了进一步验证定位算法的有效性,我们采用实际机载SAR回波进行验证,该机载SAR照射的区域包含一个已知位置的角反射器。
经过成像处理得到的图像如图7所示。

图7 实际飞行点目标位置
定位结果与实际位置的比较如表2所示。
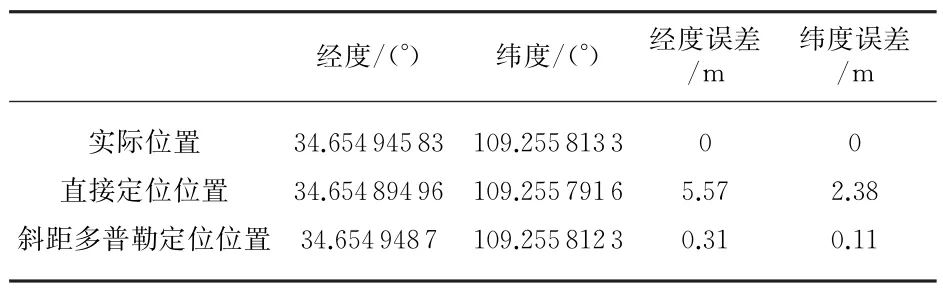
表2 实际飞行试验结果
由表2可以看出,本文介绍的直接定位精度与斜距多普勒定位精度相比,直接定位精度略差,这是因为在计算过程中,我们将地心与飞行器的连接线默认为与地面垂直导致。虽然精度略差,但是定位精度满足机载SAR图像定位精度,而且直接定位的计算量远远小于斜距多普勒定位。因此在机载SAR图像定位时,采用本文介绍的方法是可行的。
3 结束语
本文给出了一种简单的机载大作用距离定位方法,该方法定位简单,适用范围广。并且本文给出了斜视成像不同的方位压缩方式在对所成SAR图像进行定位时产生的影响。在验证试验中可以看出,在载机距离为200 km的情况下实际位置与定位位置误差小于20 m,符合定位精度要求。
[1]张耀天,孙进平,毛士艺.机载SAR图像直接定位算法研究[J].信号处理,2009,25(4):669-673.
[2]张华海,郑南山,王军,等.由空间直角坐标计算大地坐标的简便公式[J].全球定位系统,2002(4):9-12.
[3]刘佳音,韩冰,洪文.一种新的SAR图像斜距多普勒定位模型的直接解法[J].遥感技术与应用,2012,27(5):716-721.
[4]陈明,张波,单子力,等.基于两种计算模型的星载SAR定位对比分析[J].计算机工程与设计,2013,34(7):2599-2603.
[5]钱李昌,孙文峰,马晓岩.机载条带SAR图像无参考点定位技术[J].雷达科学与技术,2008,6(5):352-355.QIAN Li-chang,SUN Wen-feng,MA Xiao-yan.Locating Method of Airborne Strip-Map SAR Image Without Reference Points[J].Radar Science and Technology,2008,6(5):352-355.(in Chinese)

