一种基于改进的粒子群优化算法的神经网络PID控制器

金林骏，方建安，潘磊宁

（东华大学信息科学与技术学院，上海201620）

0 引言

多输入多输出（MIMO）控制装置由于其复杂的耦合效应，总是很难设计出一个适当的控制器。因此，多输入多输出系统的控制策略已经在工程和学术两个领域作为重点被研究多年。所有耦合回路之间的交互影响对保持良好控制系统的整体性能带来了很大的难度［1］，如何以最佳方式协调所有回路的耦合作用是一项重要的研究工作。

解耦和协调MIMO控制装置有许多多变量的控制方法，这些方法根据控制系统的工作方式不同分为多回路设计和多变量设计两大类。前者的方法是把每个变量看作为一个独立的控制对象，把变量之间的相互作用看作是扰动，通过依次迭代设定每个闭环对于其他回路的影响因子。多回路设计方法可以单独地设计闭环控制器，并且当故障发生时方便切换回单回路控制器。然而，这些方法只适用于弱耦合系统，并且难以保证其控制性能。多变量的设计方法是将多变量系统分成多个独立地单变量的子系统，然后再独立地设计各子系统的闭环控制器。然而，通过传统的多变量的设计方法（如前馈、反馈和对角矩阵解耦控制等），很难获得最实用的工业生产过程控制中对象精确的数学模型［2］，虽然可能有一些近似模型，但这些不准确模型对设计方案会产生很大的不确定性。此外，MIMO对象自身包含大量的非对称变量，也导致将这些方法应用到实际中存在许多困难。

随着人工神经网络（ANN）技术的发展，神经网络控制器可以对上述方法的缺点进行弥补［3］。作为一个通用的非线性逼近工具，神经网络能够适用于任何复杂的控制对象。它还具有一些特殊的优点，如自组织，自学习与自适应等［4］。这些特性使得神经网络控制技术成为智能控制的一个重要分支理论。无论本身或周围的环境怎样变化，人工神经网络都能一定程度地适应这种变化，所以神经网络控制器不需要依赖任何对象模型。它们可以抵抗所有的耦合关系，并且通过一个黑盒子的方法来对未知模型进行实时逼近以消除模型的不确定性。这样研究者不仅可以克服一个复杂对象建模的难度，而且可以用一种全局最优化方法实现系统的控制性能。因此，引入神经网络解耦控制器对于提高多变量控制技术是一个很好的选择。

在实际的工程应用中，著名的比例积分微分（PID）控制器仍然是一种很有用的控制器［5］。实践证明，PID控制器几乎适用于任何复杂工业过程。因此，把PID控制器和神经网络的结合到一起是一个合理的创新。一些研究者结合神经网络与PID控制器来处理一些复杂的过程。在文献［6］中，一种用神经网络控制器来线性补偿工业PID控制器的神经PID控制策略被提出并应用在机器人上。在文献［7］的飞行控制系统中，神经网络控制器与PID 相结合的控制技术用于解耦。在文献［8］中，除了结合神经网络和PID 控制器，一种改进的人工鱼群算法也被应用于控制器参数的优化。

本研究对神经网络PID控制器以及PID控制理论物理机制之间的相互作用进行研究。

1 神经网络PID 控制器的设计

传统的神经网络控制器往往缺乏高效的收敛速度和丰富的动态特性［9-10］。收敛速度慢主要是由于初始权值的随机选择；动态特性的缺失是由于在网络中缺乏物理意义，这将导致一旦网络以一个随机的方式收敛，出现过早收敛的可能性变高。这个网络需要被反复激励以达到更好的效果。为了丰富动态特性，本研究将常见的工业PID 控制理论引进神经网络控制器，并提出了神经网络PID控制器，其隐藏神经元由比例、积分和微分单元构成。通过采用PID的物理机制，神经网络PID控制器能保证避免它的收敛过程陷入局部极小，并且使它的权值都有逻辑和物理意义。

1.1 神经网络PID控制器的结构

神经网络PID控制器的结构图如图1所示。神经PID 控制器具有s个输入神经元，输入系统的控制误差为ej,j=1,2…s，3s个作为比例、积分和微分的功能单元的隐层神经元，以及s个控制对象输入信号的输出神经元。控制对象的s个输出y1,y2,...,y s再反馈给输入层，以计算控制误差。

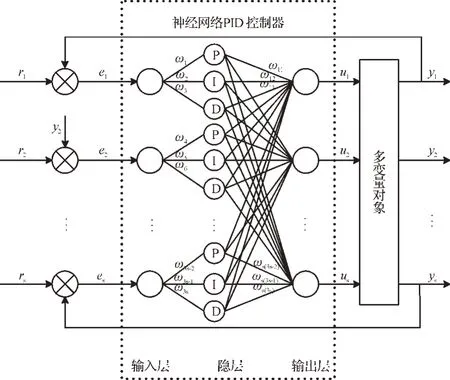
图1 神经网络PID控制器的结构图

隐层的3s个神经元分别由s个比例（P）神经元，s个积分（I）神经元和s个微分（D）神经元构成。P神经元是用来从相应的神经元输入转移成放大的电流误差控制；I 神经元是积累当前的下一个输入来对先前的控制误差求和；D神经元可以记录自己以前的状态，并且通过减去先前状态的电流输入得到控制误差的差异。每个输入层神经元都与3个隐层神经元相连，3个隐层神经元分别是P神经元、I神经元、D神经元，其连接权重分别为w3n-2、w3n-1和w3n(n=1,2,…,s)。每个隐层神经元连接所有的输出层神经元，P 神经元的连接权值为wm(3n-2)，I 神经元的连接权值为wm(3n-1)，D神经元的连接权值为wm(3n)，其中：m=1,2,…,s，

n=1,2,…,s。

输入神经元和输出神经元都以线性函数作为神经元的激励函数，隐层神经元则用下面的Sigmoid 函数作为激励函数：

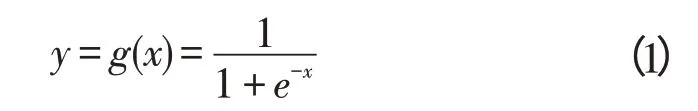
式中：x—隐层神经元输入，y—隐层神经元输出。

1.2 神经元的输入和输出

所有3层的输入、输出采样时间均为k，可以用以下公式计算。

1.2.1 输入层

在输入层有s个相同的神经元，它们的输入、输出关系是：

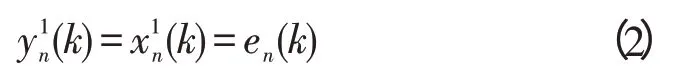
1.2.2 隐层

隐层3种不同的神经元有不同的输入和输出值。nthP神经元的输入、输出为：

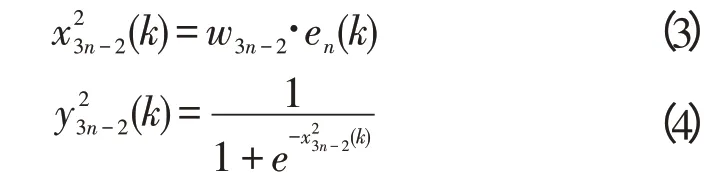
nthI神经元的输入、输出为：

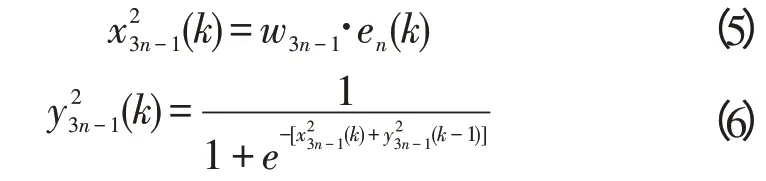
nthD神经元的输入、输出为：

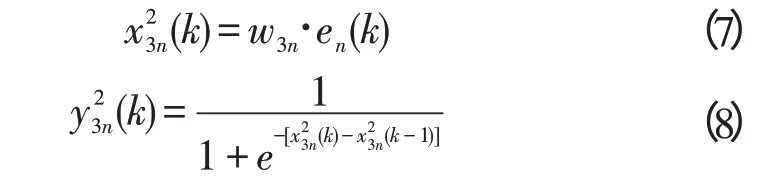
1.2.3 输出层

输出层也有s个神经元，对s个变量控制装置提供了s个控制信号，所以的隐层神经元对每一个输出层神经元的输出值都有影响。因此，输出层神经元的输出可以被计算如下：

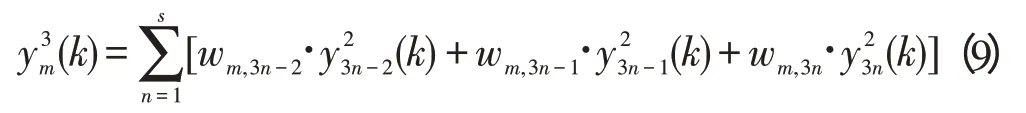
1.3 神经网络PID控制器的学习算法

神经PID 控制器仍然是一个神经网络，运行在操作对象上，并以通过持续的调整它的连接权值来达到减少控制误差的目的，这个修改方向的学习算法主要是基于梯度下降法。为了保证控制系统的稳定性，学习步长的约束条件按照李雅普诺夫稳定性理论来设定。

在所提出的神经网络PID 控制器中，输入层和隐层之间的连接权重只负责数据从输入层传向隐层，它们不会对控制器的最终性能造成很多影响。隐层和输出层之间的连接权重是控制工作性能的主要影响因素，这些权重主要是来消除控制对象的耦合效应，他们的值可以通过控制器来决定。因此，连接权值wm(3n-2)、wm(3n-1)和wm(3n)（m=1,2,…,s，n=1,2,…,s）是可以被修改的。首先，用下面的矢量描述系统的控制误差：

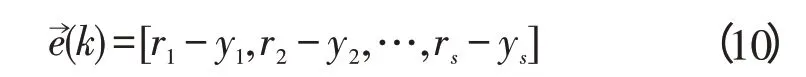
式中：ri,yi—控制系统的输入和输出，i=1,2,…,s。

然后定义以下矩阵：

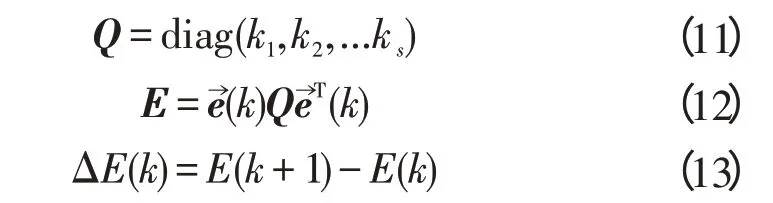
式中：Q—一个对角单位矩阵，k1=k2=...=ks=1。

然后定义一个李雅普诺夫函数，如下：

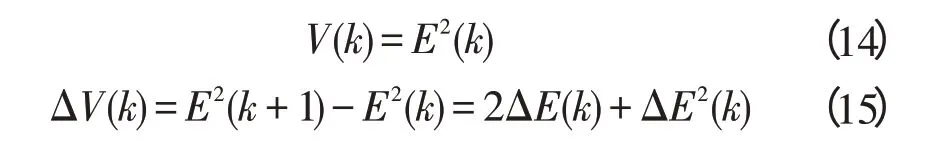
根据梯度下降法，这个调整应为：

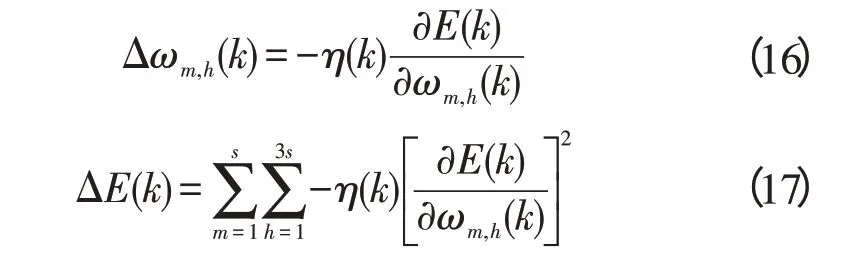
其中：m=1,2,…,s；h=3n-2,3n-1,3n；n=1,2,…,s；η(k)—在采样时间k时的学习步长。

把式（17）代入式（15），并假设ΔV(k)＜0，则可以得到下式：

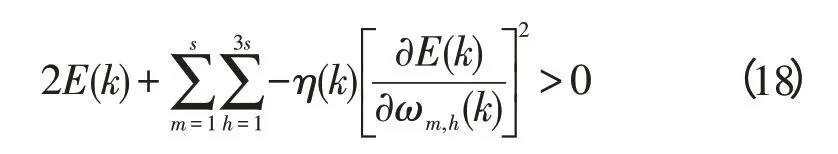
当学习步长满足式（18），该系统可以满足李雅普诺夫稳定性。为编程方便，本研究设置可变学习步长η(k)，按照下列的式（18）约束为一固定值η：

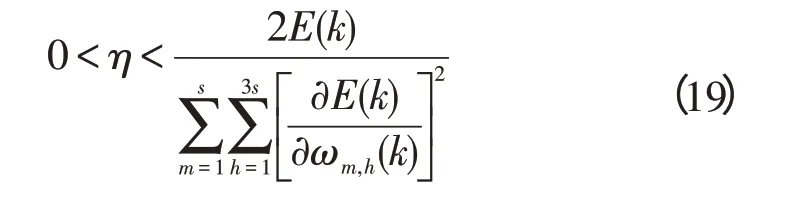
2 神经网络PID 控制器的优化

虽然PID 机制给了连接权值逻辑和物理意义，但是连接权值的最初设定值仍然对收敛速度有很大的影响。权重的随机初始化会给控制器带来很多不确定的因素，使控制器难以达到其最佳性能。为了加速收敛过程，该优化算法用最小化控制误差的方法来获得合适的初始权值。

2.1 改进的粒子群优化算法

所有的优化算法中，粒子群优化（PSO）算法由于它的高速收敛性，是目前最流行的一种优化算法。它是由肯尼迪和艾伯哈特在1955年提出来的［11］。其想法来源于进化计算的理论，该算法模拟鸟群觅食的行为，通过每个鸟群之间的合作找到食物源。不同于无规则的演变过程，PSO算法可以使进化变得有规律，并且通过各单位之间的信息共享机制，来获得最佳的解决方案。

在q空间中p的一组粒子，粒子ith(1 ≤i≤p)有一个速度和方位在cth的迭代搜索，定义最优解为粒子i直到当前迭代为，对于所有粒子直到当前迭代的最优解决方案为，则i粒子在下一次迭代的位置和速度使用下列公式进行更新：

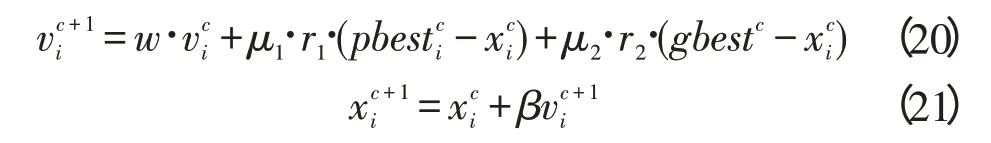
式中：w—惯性权重；μ1，μ2—学习因子；r1，r2—［0，1］之间的一随机数；β—一个速度约束因子，i=1,2,…,p，c=1,2…G（G是最大迭代）。速度的区间表示为，位置的区间表示为，如果更新值的速度或位置是超过设定的区间，则取区间的相应边界值。

然而，传统PSO 算法不收敛的风险仍然存在，这对控制系统来说很可能是一个潜在的危险。因此，本研究提出了一种改进的方法，可以实现种群的多样性之间的平衡，并且在速度更新公式中通过加入收缩因子来加快收敛速度。对速度进行进一步限制的改进的粒子群优化算法（IPSO），已被证明是一种有效的数学理论。现在速度的更新公式如下：

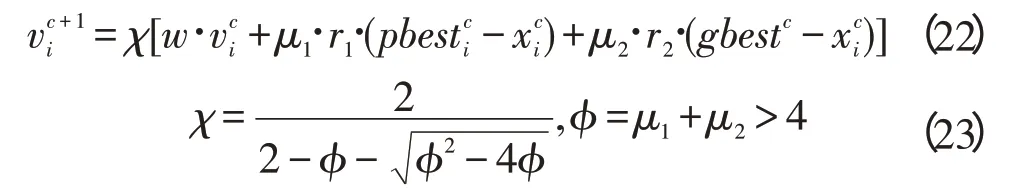
目标函数确定后，详细的IPSO算法的优化步骤如下：

（2）所有粒子的更新的速度和位置根据等式（22，21），把它们限制在区间范围内。

（3）对于每个粒子，目标函数用位置更新的方法去计算新的适合度值。如果新的位置比原先的位置对个体优化更好，那么就用新的值取代个体优化值，否则，则优化值不变。

（4）用个体的最优确定全局最优的新值。

（5）如果满足终止条件，则算法停止。否则则返回步骤（2）。

由于快速收敛速度，该IPSO 算法易于实现，只有几个参数需要调整，这些特性使他可以应用到如系统控制、模式识别和通信工程等许多不同的领域。

2.2 网络初始权值的优化

由于隐层和输出层之间的权值是需要调整的。优化过程中还针对这些权重。首先，把权重编码到多维向量，如下：

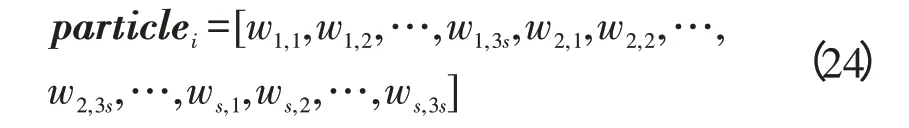
设定目标函数绝对误差积分（IAE）指标：

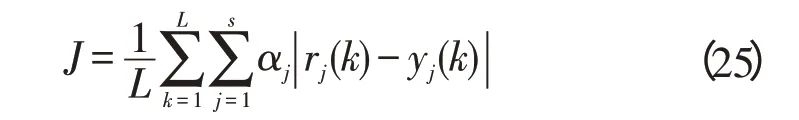
式中：L—给定的采样长度；α1,…,αs—每个控制误差的影响因子，然后粒子的训练可以以目标函数的倒数来进行计算：

以最小化IAE指标综合的目的，IPSO算法可以决定神经PID控制器的最优初始连接权值。优化过程的流程图如图2所示。

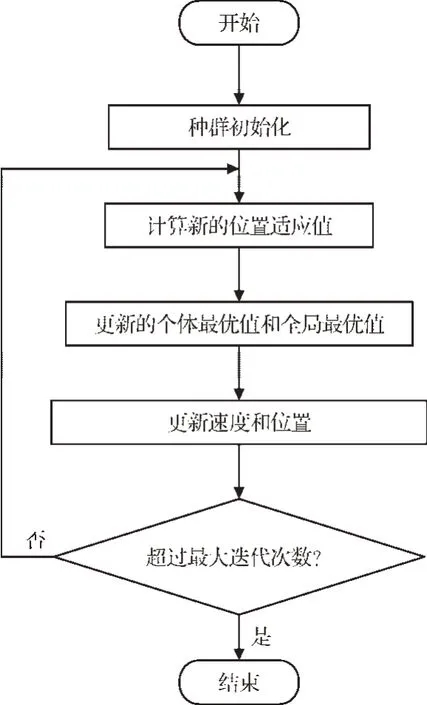
图2 优化流程图

这个过程将在神经网络PID控制器的初始化过程中运行。在那之后，神经网络PID 控制器用第3 章介绍学习算法下调整它的权重。

2.3 控制系统的操作步骤

在优化过程中，神经PID 控制器对于MIMO 控制装置更加可靠。整个控制系统的结构图如图3所示。

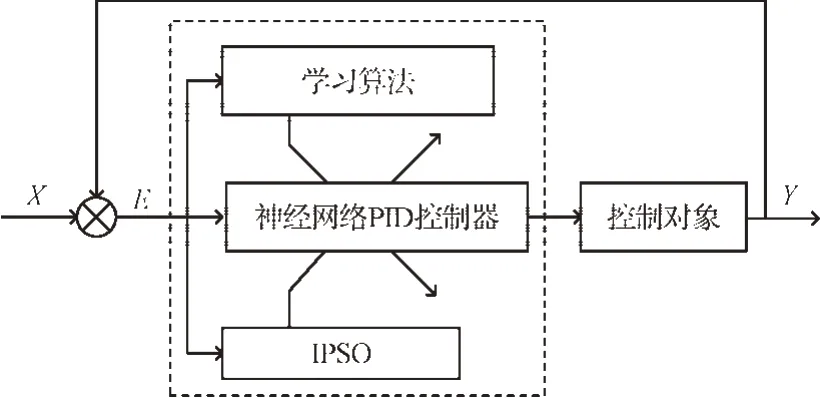
图3 控制系统的结构图

其操作步骤证明如下：

步骤1：把控制对象输入到控制器中；

步骤2：IPSO 算法的神经网络PID 控制器权值初始化，在这期间，学习算法不工作在控制器中；

步骤3：用神经网络PID控制器控制MIMO对象；

步骤4：将控制系统的输出反馈到神经PID 控制器；

步骤5：通过给出的学习算法调整神经网络PID控制器的连接权值。

步骤6：如果控制系统达到稳态，意味着的控制误差已经足够小，此时终止学习算法。否则，不断调整学习算法的权值。

3 应用及仿真

为了验证所提出的神经网络PID控制器以及改进算法的有效性，本研究选择了一个复杂的非线性有3个变量的控制对象，并且该对象具有较强的耦合效应：

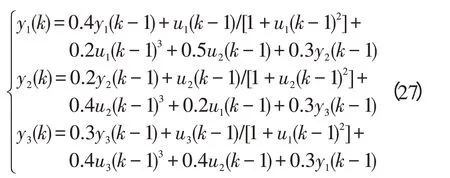
神经网络PID控制器的说明图1是用来控制上述对象的。仿真实验是在有优化及没有优化两种情况下所做的，以测试IPSO算法的有效性。这两种情况下设置控制目标为［0.7，0.4，0.6］，控制信号的初始值设定为［0，0，0］，设定学习步长η=0.5，采样时间为0.001 s，在没有优化的情况下，权重随机初始化。

仿真结果如图4～6所示，证明未经优化的神经网络PID控制器在一定程度上可以维持控制系统的稳定性，但其准确性不够好。而经过优化的神经网络PID控制器不仅可以确保系统的稳定性，并且提高了系统的精确性及快速响应性。这说明了所提出的IPSO 优化算法神经网络PID控制器在MIMO控制对象中可以实现良好的性能。

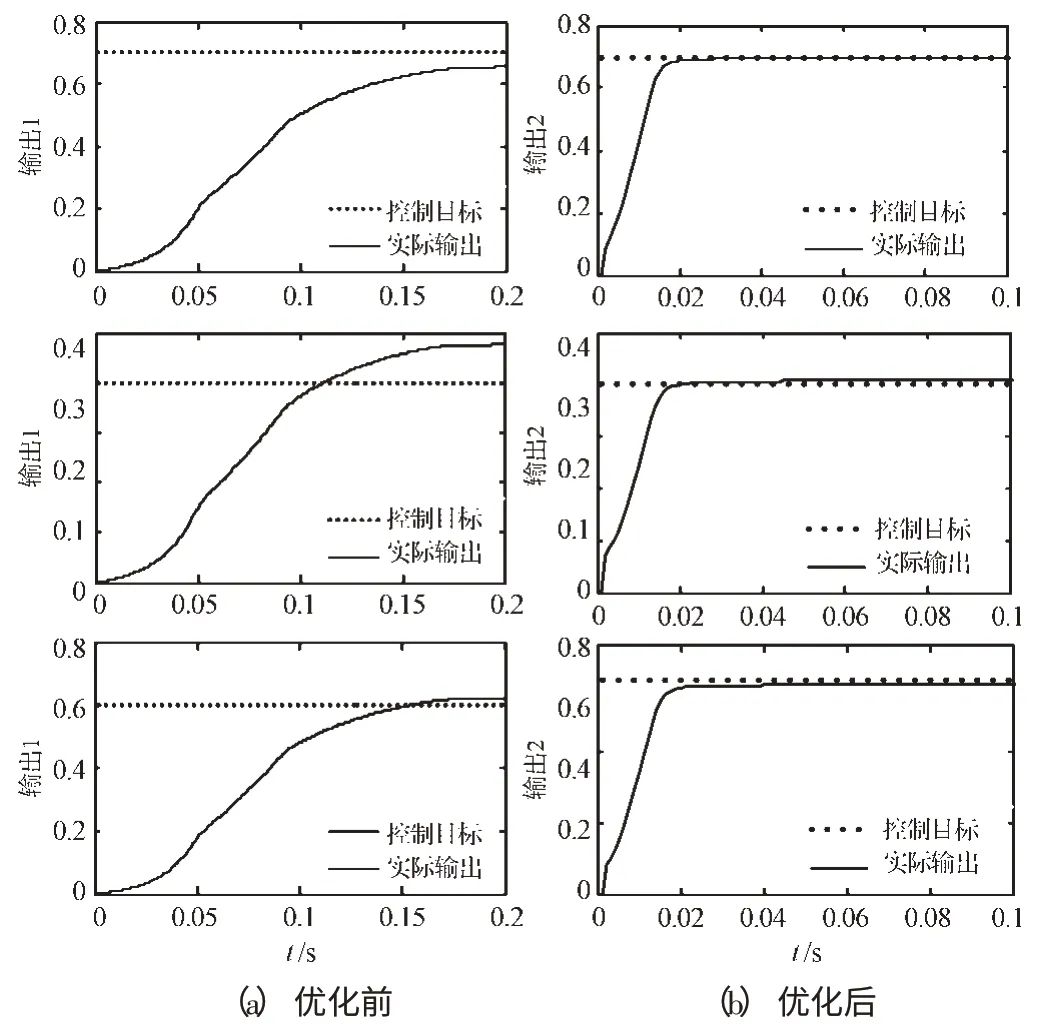
图4 响应曲线的比较

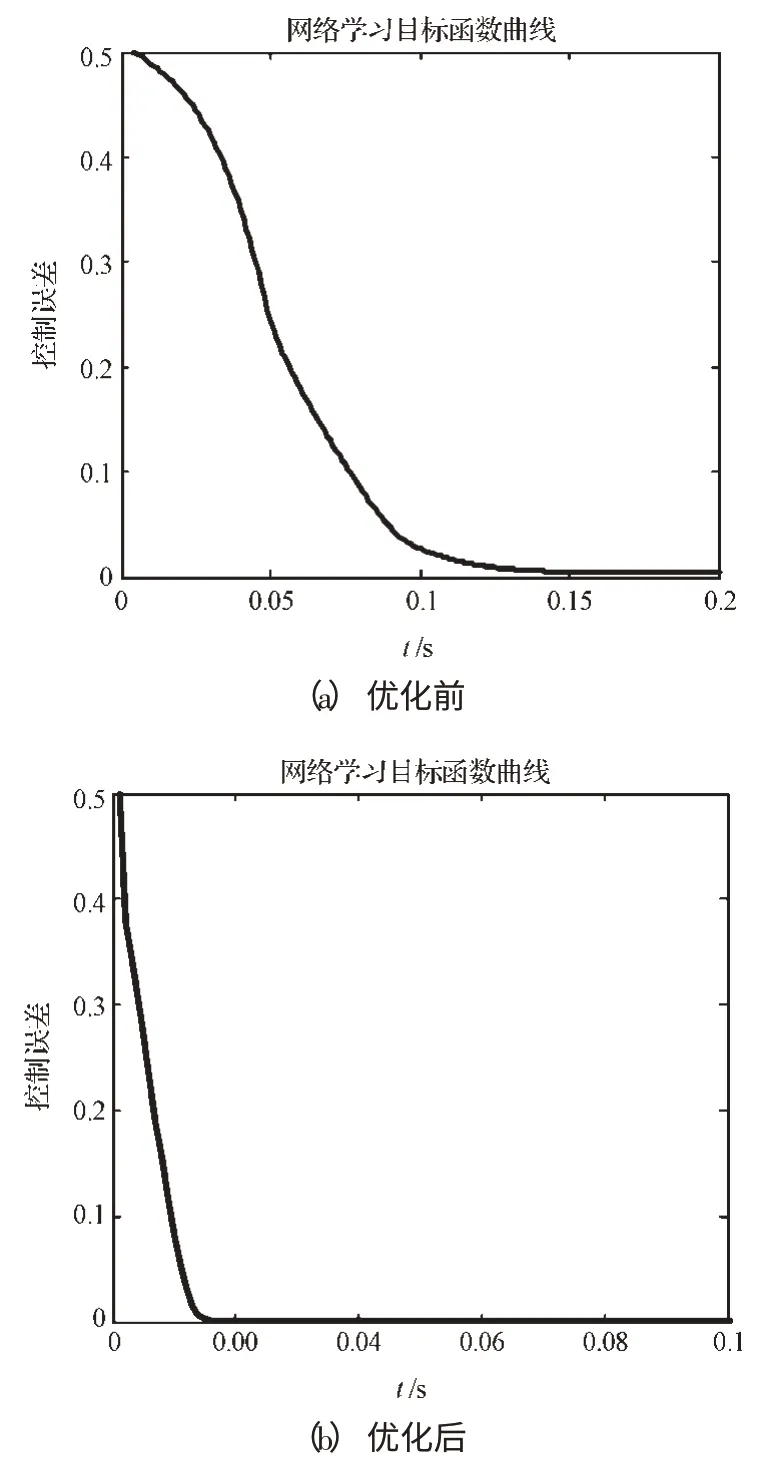
图5 目标函数曲线的比较

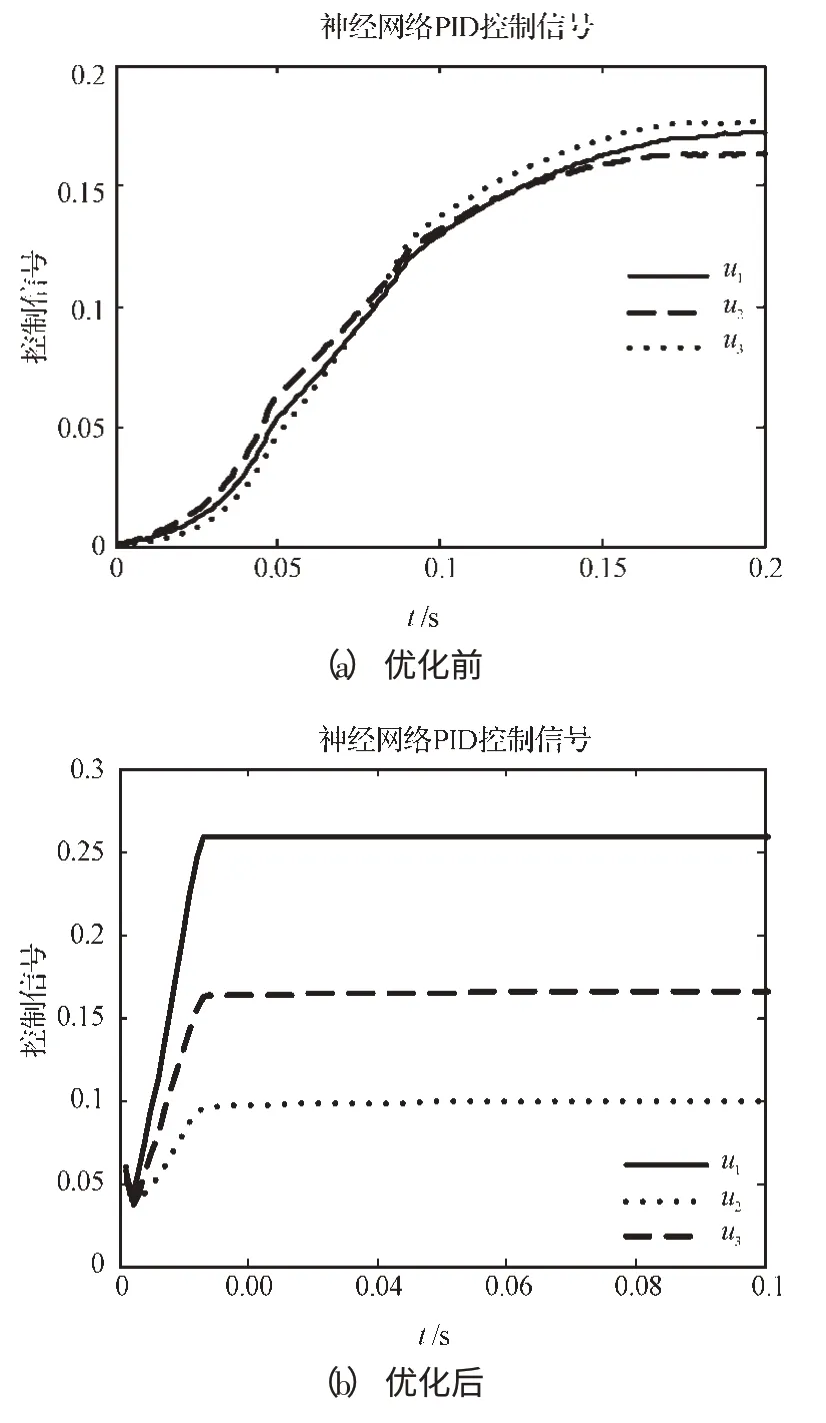
图6 控制信号的比较

4 结束语

本研究通过将PID控制机制和神经网络控制技术相结合，可以使这两种方案的优势充分展现出来。神经PID控制器被证明可以有效地处理多输入多输出过程，再加上IPSO 优化算法，神经网络PID 控制器便可以具有更优良的控制性能。

因此，本研究所提出的神经网络PID 控制器IPSO优化算法对于有较强耦合效应的MIMO控制对象是一个很好的选择。

（References）：

［1］李付军，雒宝莹，曾军高，等.3 轴电动转台动力耦合分析及抑制策略［J］.上海交通大学学报，2011（2）：202-207.

［2］XU Shun-gang，WANG Jin-ping，XU Jian-ping.A current decoupling parallel control strategy of sing-phase inverter with voltage and current dual closed-loop feedback［J］.IEEE Transactions on Industrial Electronics，2013（4）:1306-1313.

［3］DONG Xiu-cheng，ZHAO Yun-yuan，XU Yun-yun，et al.Design of PSO fuzzy neural network control for ball and plate system［J］.International Journal of Innovative Computing，Information and Control，2011，12（7）：7091-7103.

［4］徐 文，王大忠，周泽存，等.结合遗传算法的人工神经网络在电力变压器故障诊断中的应用［J］.中国电机工程学报，1997（3）：109-112.

［5］SHA Li-zheng，GAO Jun，WANG Jian-hua.Pulp Concen⁃tration Control by PID with BP Neural Network in the Pro⁃duction of Light Weight Cardboard［C］//2010 IEEE 11th In⁃ternational Conference on Computer-Aided Industrial De⁃sign & Conceptual Design（CAIDCD）.Yiwu：［s.n.］，2010:1217-1220.

［6］YU Wen，ROSEN J.Neural PID control of robot manipula⁃tors with application to an upper limb exoskeleton［J］.IEEE Transactions on cybernetics，2013，43（2）:673-684.

［7］程 波，何贵波，李 天.PID神经网络在飞控解耦中的仿真研究［J］.电光与控制，2012（6）：41-44.

［8］冯冬青，马超阳，刘艳红.基于人工鱼群的PID神经网络非线性系统控制［J］.计算机仿真，2012（9）：247-250.

［9］王衍平.单神经元PID 算法在包装机温控系统中的应用［J］.包装与食品机械，2013（3）：69-72.

［10］李 明，杨 承，舒 宇.一种全局收敛的神经网络PSO训练算法［C］//2007′仪表，自动化及先进集成技术大会论文集（二）.重庆：重庆大学，2007：533-537.

［11］纪雪玲.改进粒子群优化算法及其在人工神经网络中的应用研究［D］.昆明：西南林业大学机械与交通学院，2012.