一种电气化铁路牵引网电磁暂态建模方法*

孙 科，江全元

(浙江大学电气工程学院，浙江杭州310027)

0 引言

近年来，针对电气化铁路牵引供电系统的仿真分析研究也成为重要研究内容［1］。传统的仿真分析研究主要集中在牵引网的潮流计算分析［2-5］，而目前针对牵引网谐波、短路以及操作过电压等暂态过程需要的电磁暂态仿真研究主要都是通过现有电磁仿真工具实现的［6-7］。这种研究的局限性在于:①软件仿真模块基本针对电力系统设计，对于牵引网特性支持不完全;②仿真软件针对大规模长线路的牵引网详细仿真模型建立步骤繁琐，不能方便调节仿真参数;③仿真软件算法封装，程序二次开发能力差，无法针对牵引网进行优化。

本研究从牵引网各电气设备基本模型出发，建立一套针对牵引网的电磁暂态仿真模型，并针对牵引网结构进行算法设计，简化建模步骤，为算法优化提供接口。

1 牵引网电磁暂态模型概述

1.1 牵引网供电方式

电气化铁路牵引网通常的供电方式包括有:直接供电方式(TR)、带回流线的直接供电方式(TRNF)、吸流变压器供电方式(BT)、自耦变压器供电方式(AT)、同轴电力电缆供电方式(CC)、混合供电方式(直接供电方式+AT 供电方式)等［8-10］，其中在我国高速铁路中主要采用了TRNF 供电方式和AT 供电方式。在进行牵引网的电磁暂态建模时，传统研究方式需要按照牵引网所采用的供电接线方式来建立相关模型。

1.2 牵引网统一电磁暂态模型

上述所提及的牵引网供电方式，从整体上看，都可以认为牵引网的主线路是平行多导体传输线，而其他电气设备则可以看作并联元件和串联元件分布在线路中。其中，主要电气设备划分归类如表1所示。

表1 牵引网主要电气设备类型划分

在进行牵引网电磁暂态建模时，整个网络模型都等效为电阻网络和电流源组合的形式。本研究针对串联元件和并联元件，先忽略外部影响，得到独立的元件模型。在进行仿真计算时，笔者在系统相应节点的导纳矩阵和节点注入电流源处添加各元件对应元素，再联立求解，即可得全系统的解。假设整个牵引网有n条导线，按照牵引网串联元件与并联元件空间距离分布将牵引网导线以元件为切面分割成K 段，其中切面k 和k+1 间的线路模型示意图如图1所示。

图1 牵引网统一模型示意图

并联元件和串联元件模型的节点电压方程通用表达式为:

式中:G—并联元件的导纳矩阵，n ×n 的方阵;J—等效节点注入电流源，n 维向量;串联元件连接了2n 个节点，形成的导纳矩阵G 为2n ×2n 的方阵，等效节点注入电流源J 为2n 维向量。

本研究采用上述建模方式对牵引网进行建模，相比于利用现有的电磁暂态仿真工具，其优点包括:①采用统一的建模方式，适用于不同牵引供电方式的牵引网;②在处理AT 供电方式、CC 供电方式等需要对牵引网单一供电臂导线进行多段分割的情形时，能够便捷实现;③在仿真过程中，能够在机车实际运行位置处动态加入等效机车注入电流源，而不用修改仿真工具中的模型。

2 牵引网电气元件电磁暂态模型

在牵引网的电气元件电磁暂态模型中，特别考虑了牵引网导线、牵引变压器、自耦变压器的模型，其他电气设备的模型可以参考稳态模型类似推导。

2.1 牵引网导线电磁暂态模型

牵引网导线模型是牵引网模型研究的基础，其采用的电磁暂态仿真模型参考了电力系统输电线模型［11-15］。本研究根据多导体线路波过程建立基本波动方程，将所得的多相耦合线路模型通过相模转换解耦，等效为在模坐标内相互独立的传输线，并进行电磁暂态计算公式推导，最后在相坐标下建立节点电压方程。

2.1.1 单根输电线电磁暂态模型

以送端s 端为例，建立的电磁暂态模型为:

式中:L，C—线路单位长度的电感和电容;x—与送端的距离;Z—波阻抗，τ—线路上波传播时间，l—线路长度。

2.1.2 牵引网导线相模变换

利用相模变换矩阵将方程由相坐标转换到模坐标进行求解，再进行后续计算。

设相模变换矩阵为Q，获得相模变换为:

式中:Um，Im——模坐标下电压、电流;

可以参考单根输电线电磁暂态模型获得平行多导体导线在模坐标下的计算模型，对于s 端有:

式中:Ym——模坐标下导纳矩阵，为各模量波阻抗倒数组成的对角阵，Ym=(Zm)－1;

2.1.3 牵引网导线节点电压方程

对整个牵引供电系统进行电磁暂态仿真时，需要将得到的模坐标下的多导线模型转换到相坐标下，进而建立节点电压方程求解。

仍以s 端为例，根据相模转换公式，模坐标下的公式转换到相坐标后为:

式中:Y—相坐标下导纳矩阵，Y=QYmQT。

对于电气化铁路牵引网平行多导体导线，由于其在每隔一段距离就会存在线路间的短接或者接地，需要按照实际线路连接步长将牵引网导线划分为多段进行处理。针对传输距离并不长的导线，研究者可以用集中在线路两端的电阻网等效模拟沿线路均匀分布的电阻，得到集中等效到线路两端的电阻网络矩阵Rl:

仍以s 端为例，假设有n 条牵引网导线，则可以得到牵引网导线的节点电压方程为:

2.2 牵引变压器电磁暂态模型

通常情况下，电气化铁路采用的是非对称式接线方法，将上、下行的牵引供电网接入电力系统三相供电网。牵引变压器最常用的接线方式是三相V/v 接线，广泛应用于京津、京沪等高铁线路中。

2.2.1 单相变压器电磁暂态模型

针对一阻抗支路建立电磁暂态模型，这是组成变压器励磁支路和等效漏电感支路的模型基础。利用隐式梯形积分法得到离散化计算方程为:

式中:in+1，un+1—n +1 时刻的支路电流及支路电压;G—支路等效导纳，G=h/(2L +hR);Jn—n 时刻历史注入电流，Jn=Gun+(2L－hR)in/(2L +hR);h—计算步长。

对于单项变压器，通常使用等效电路进行建模，将变压器一次侧和二次侧的漏电阻和漏电抗都等效集中到二次侧，将变压器的励磁电感等效并联在一次侧。

本研究推导其电磁暂态模型主要采用受控源模型来等效理想变压器［16-18］，可以获得其等效电路图如图2所示。

图2 基于受控源的单相双绕组变压器模型

可以得到变压器的矩阵模型方程为:

2.2.2 三相V/v 接线变压器电磁暂态模型

三相V/v 接线中一次侧中有一相进线与另一相出线首尾相连，采用和单相变压器相同处理方法，可以获得三相V/v 接线变压器基于受控源的等效电路图如图3所示。

图3 基于受控源的三相V/v 接线变压器等效电路

由此可以得到变压器的矩阵模型方程。

2.3 自耦变压器电磁暂态模型

本研究采用基于受控源的自耦变压器模型，同时考虑了自耦变压器磁耦合和直接电耦合的特点［19-20］。

本研究将单相双绕组自耦变压器的公共绕组以及串联绕组的漏阻抗都等效到一次侧，建立的模型等效电路图如图4所示。

图4 基于受控源原理的单相双绕组自耦变压器模型

得到变压器的矩阵模型方程为:

2.4 其他并联元件

2.4.1 并联阻抗元件

在牵引网计算中，可以用并联阻抗元件描述网络中的并联补偿装置、无源滤波装置等。基本的结构为两导线间并联阻抗或者一导线与地并联阻抗。其他并联形式都可以分解为基本形式后叠加得到。

当两导线间并联阻抗时，可以得到元件节点电压方程为:

当一导线与地并联阻抗时，可以得到元件节点电压方程为:

2.4.2 横向连接和短路故障

横向连接包括了牵引供电方式中线路的金属性连接，AT 供电方式中的CPW 线、BT 供电方式中的吸上线等都可用该模型描述。短路故障在仿真计算中也采用和横向连接类似的方法。

实质上，横向连接和短路故障的金属性连接都是用很小的电阻等效，属于并联阻抗元件的特殊情况，其元件节点电压方程为:

当两导线间发生连接时:

当一导线与地发生连接时:

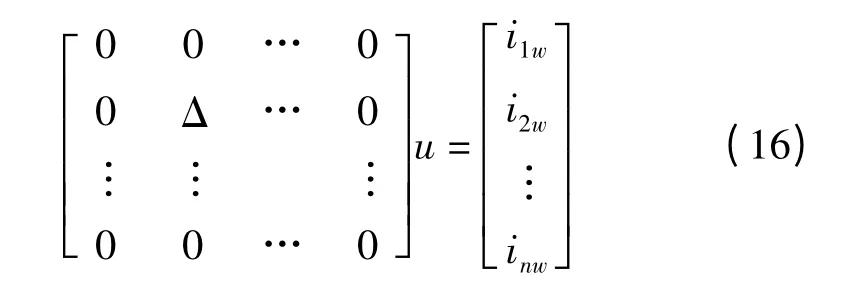
式中:Δ—1 很大的实数，可取1012。

2.4.3 电力机车

在牵引网仿真分析过程中，机车一般等效为在接触线和钢轨之间并联的元件，随运行时间在系统切面上移动。通常工程中采用等效电流源来模拟机车，而更精确的计算需要按照详细的建模仿真得出。本研究主要讨论牵引网的模型，故机车选取了电流源模型来模拟。

2.5 其他串联元件

2.5.1 串联阻抗元件

串联阻抗元件可以用来模拟线路中串联的无源RLC 元件，形成的节点导纳矩阵为2n ×2n 的方阵，节点电压方程为:

2.5.2 断线故障

断线故障可以看做阻抗很小的串联阻抗元件，等效模型中，等效注入电流源为0，等效导纳为很小的实数，可以取10－6。

3 牵引网电磁暂态仿真计算

3.1 牵引网电磁暂态节点电压方程建立

笔者已经介绍了牵引网整体模型的建立方法，现本研究以AT 供电方式为例介绍牵引网电磁暂态节点电压方程建立过程。

在建模时，因牵引网中某些导线持续性并联，可简化计算将这些导线合并。AT 供电方式中通常是将左、右平行的钢轨合并、接触线和承力索合并。

方程建立首先根据牵引网电气元件SS、AT 等的空间位置分布以及CPW、接地装置间距和机车位置，分割牵引网导线，使每段导线两端都连接不同空间位置的牵引网电气元件。整个系统计算节点由此确定划分。

然后对系统节点电压方程的导纳矩阵和等效注入电流源，按照各电气元件的独立模型，添加对应项，最后建立节点电压方程:

式中:Un+1，Un+1—n +1 时刻的节点电压和电源节点注入电流;Y—系统导纳矩阵;Jn—n 时刻的等效节点注入电流，由各电气设备和牵引网导线模型中等效电流源计算得出。

3.2 牵引网电磁暂态计算方法

牵引网电磁暂态仿真计算的步骤如下:

步骤1。根据牵引网导线空间分布和参数，计算其分布参数，同时求解相模转换矩阵，获得转换后的参数矩阵;

步骤2。根据牵引网上电气设备及接地装置分布，将牵引网导线分割，根据牵引网元件模型，建立牵引网全线的节点电压方程;

步骤3。利用牵引网潮流计算程序获得牵引网各计算节点的初值;

步骤4。判断是否有短路、断路、开关闭合等改变系统拓扑结构的操作。若有，则按此修改系统的导纳矩阵和等效注入电流源项。

步骤5。根据历史电压电流数据，计算各节点处的等效电流源注入电流，包括电力系统电网、牵引网导线、牵引变压器、自耦变压器等，同时根据机车当前运行位置，在对应计算节点处添加机车注入电流。

步骤6。求解当前时刻点节点电压方程，记录计算结果，同时针对牵引网导线计算模坐标下的电压电流。

步骤7。重复步骤4、5、6，其中步骤5 中的历史电压电流数据采用上一时步中步骤6 计算所得结果。循环计算，直至仿真时刻到达设定的仿真结束时间为止。

4 算例分析

根据本研究提出的牵引网电磁暂态仿真计算方法，编写了牵引网电磁暂态计算程序。采用一AT 供电方式的牵引网进行仿真算例计算，该牵引网导线型号和空间分布如图5所示，电气设备位置分布如表2所示。牵引变压器一次侧接入220 kV 电网，二次侧电压为2 ×27.5 kV，牵引变压器容量为63 MVA，牵引变压器短路阻抗8.6%，钢轨泄漏电阻为10 Ω/km，每隔5 km 钢轨-保护线经CPW 线连接，同时保护线经小电阻接地，小电阻阻值1 Ω［21-22］。

图5 牵引网导线空间分布图

表2 测试牵引网变电所位置分布

4.1 沿线电压分布分析

测试算例利用等效注入电流源模拟机车电流注入，机车运行至距起始点27.84 km 处，注入电流为950 A。

牵引网接触线沿线的电压有效值图如图6所示，包括了采用本研究方法的电磁暂态计算程序和PSCAD 仿真所得结果。笔者分析了采用本研究提供的电磁暂态计算方法和采用PSCAD 仿真获得的沿线接触线电压分布的误差，分析结果如表3所示。

图6 牵引网接触线沿线分布电压

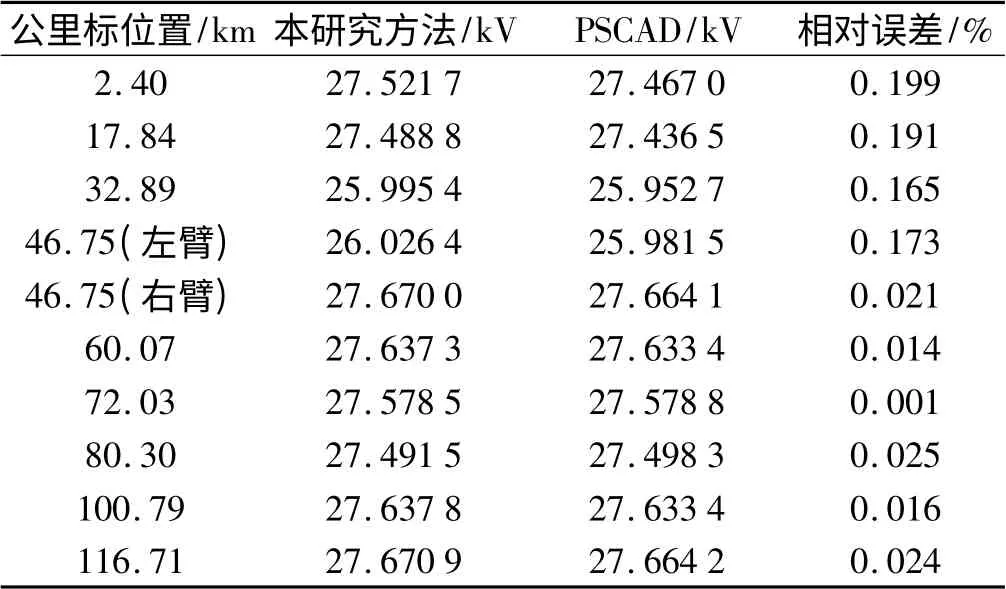
表3 牵引网接触线沿线分布电压误差比较

结果表明，在机车运行处牵引网接触线有明显的电压降。采用本研究方法建立的牵引网电磁暂态仿真计算与PSCAD 计算在稳态时电压空间分布基本一致，相对误差均在0.2%以内，说明本研究方法能够准确反映牵引网运行状况。

4.2 短路故障分析

测试算例分析了牵引网接触线发生接地短路和发生牵引线负馈线线间短路时的短路电流。机车运行到距起始点85.3 km 处，在距离起始点95.3 km 处发生短路故障。

4.2.1 接触线接地短路

当发生接触线接地短路时，牵引变TPS2 接触线右臂出口处的短路电流计算结果与PSCAD 仿真结果比较如图7所示。

图7 发生接触线接地短路时电流

结果表明，在发生牵引网接地短路瞬间电流增大而后趋于平稳。本研究通过对图7 的仿真结果误差进行分析，得到两种方法的均方根差值为34.17 A，以1 kA为基准时相对误差3.42%，两种方法仿真结果基本一致。基于本研究算法的程序能够反映牵引网发生接触线接地短路时系统运行状况。

4.2.2 接触线和负馈线线间短路

当发生接触线负馈线接地短路时，牵引变TPS2接触线右臂出口处的短路电流计算结果与PSCAD 仿真结果比较如图8所示。

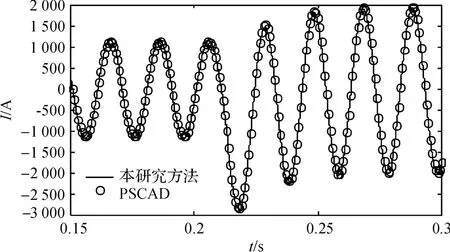
图8 发生接触线负馈线线间短路时电流

结果表明，在发生牵引网接触线线间短路瞬间电流增大而后趋于平稳。通过对图8 的仿真结果误差分析，得到两种方法的均方根差值为33.23 A，以1 kA 为基准时相对误差3.23%，两种方法仿真结果基本一致。基于本研究算法的程序能够反映牵引网发生接触线负馈线线间短路时系统运行状况。

4.3 断路故障分析

测试算例时，分区所开关闭合，牵引变SP1 和SP2同时为两牵引变间公共线路供电。机车运行至距起始点65.07 km 处，在距离起始点77.03 km 处发生接触线短路故障，原来由SP1 和SP2 双牵引变供电的机车变为只由TPS1 单牵引变供电，机车处的接触线电压的计算结果和PSCAD 仿真结果比较如图9所示。

图9 发生断线故障时接触线电压

结果表明，当机车由双牵引变供电因断线故障变为由较远的牵引变供电时，机车所处位置接触线电压幅值降低。通过对图9 的仿真结果误差分析，得到两种方法的均方根差值为0.603 kV，以27.5 kV 为基准时相对误差2.19%，两种方法仿真结果基本一致。基于本研究算法的程序能够反映牵引网断路故障时系统运行状况。

4.4 算法优势

通过上述算例分析表明，采用本研究算法进行牵引网电磁暂态仿真，能够准确有效地反映牵引网电磁暂态过程的运行状态。而相比于传统地利用PSCAD进行仿真计算，本研究算法的优势包括:

(1)针对牵引网开发，建立模型以及修改模型参数操作方便，适用于多种牵引网络结构，特别是针对分段较多的长牵引网线路，相比于PSCAD 拖动模型模块搭建过程，极大地减少了操作量;

(2)能够支持牵引线导线采用不同参数的情形，克服了PSCAD 模型上的不足;

(3)算法过程可控，建立的节点电压方程为对角分块矩阵，各分块矩阵间相互解耦，可作为后续进行计算并行化的基础进行二次开发。

5 结束语

本研究针对牵引网提出了统一电磁暂态模型体系，建立了包括牵引网导线、牵引变压器、自耦变压器在内的电气设备的电磁暂态模型。并提出了基于牵引网电气设备分布，分割牵引网导线，建立牵引网全线的电磁暂态节点电压方程的计算方法。该方法能够根据针对不同供电接线方式的牵引网系统建立全线的电磁暂态模型。但本研究的牵引网电磁暂态模型主要集中在理论性的探讨，所采用的牵引网电器元件模型相对比较简单，与实际牵引供电系统还有一定的差距。

［1］李 芾，安 琪，王 华.高速动车组概论［M］.成都:西南交通大学出版社，2008.

［2］何正友，方 雷，郭 东，等.基于AT 等值电路的牵引网潮流计算方法［J］.西南交通大学学报，2008(2):1-6.

［3］郭 东，杨建维，何正友，等.一种基于牛顿法的交流高速铁路牵引供电潮流计算方法的研究［J］.继电器，2007，35(18):16-29.

［4］吴命利.电气化铁道牵引网的统一链式电路模型［J］.中国电机工程学报，2010，30(28):52-58.

［5］陈宏伟，耿光超，江全元.电气化铁路牵引供电系统车网耦合的潮流计算方法［J］.电力系统自动化，2012，36(3):76-80.

［6］LEE H M，LEE C，JANG G.Harmonic analysis of the korean high-speed railway using the eight-port representation model［J］.IEEE Trans on Power Delivery，2006，21(2):979-986.

［7］张 扬，刘志刚.基于电磁暂态分析的高速铁路牵引网谐波模型及谐波特性分析［J］.电网技术，2011，35(5):70-75.

［8］李群湛，贺建闽.牵引供电系统分析［M］.成都:西南大学出版社，2007.

［9］李保霞.行李车DC 600 V 供电系统改造设计［J］.2014(S1):157-158.

［10］谭秀炳.交流电气化铁道牵引供电系统［M］.成都:西南交通大学出版社，2006.

［11］DOMMEL H W.Computation of electromagnetic transients［J］.Proc IEEE，1974，62(7):983-993.

［12］DOMMEL H W.Digital computer solution of electromagnetic transients in single and multiphase networks［J］.IEEE Trans on Power Apparatus and Systems，1969，88(4):388-399.

［13］吴维韩，张芳榴，刁颐民.多导线输电线路上波过程的贝杰龙计算方法［J］.高电压技术，1981(4):9-24.

［14］徐 政.耦合长线电磁暂态分析的扩张Bergeron 模型［J］.中国电机工程学报，1996，16(5):354-357.

［15］NGUYEN H V，DOMMEL H W，MARTI J R.Direct phase-domain modelling of frequency-dependent overhead transmission lines［J］.IEEE Trans actions on Power Delivery，1997，12(3):1335-1342.

［16］LEON F D，SEMLYEN A.Complete Transformer Model for Electromagnetic Transients［J］.IEEE Trans actions on Power Delivery，1994，9(1):231-239.

［17］彭龙生.暂态保护AD 模块开发［J］.机电工程技术，2014(12):111-113.

［18］赵亮亮.电力系统电磁暂态数字仿真中自耦变压器模型的研究［D］.天津:天津大学电气工程学院，2004.

［19］朱 翊.电力变压器电磁暂态仿真模型与算法研究［D］.天津:天津大学电气工程学院，2012.

［20］王庆平，董新洲，周双喜.基于自适应模型的变压器暂态全过程数值计算［J］.电力系统自动化，2004，28(18):54-58.

［21］余丹萍.电气化铁路牵引供电系统的仿真及影响研究［D］.杭州:浙江大学电气工程学院，2011.

［22］余丹萍，周 盛，江全元.CRH3 型动车组牵引传动系统的直接转矩控制研究［J］，机电工程，2010，27(10):62-67.