非对称成本扰动信息下双渠道供应链的契约设计

彭 静，林 杰，林 正

（1.同济大学经济与管理学院，上海200092；2.浙江农林大学信息工程学院，浙江临安311300；3.浙江省特种设备检验研究院，浙江杭州310020）

非对称成本扰动信息下双渠道供应链的契约设计

彭 静1，2，林 杰1，林 正3

（1.同济大学经济与管理学院，上海200092；2.浙江农林大学信息工程学院，浙江临安311300；3.浙江省特种设备检验研究院，浙江杭州310020）

研究由单制造商和单零售商组成的双渠道供应链系统在非对称的生产成本扰动信息下的契约设计问题.使用委托代理理论，通过求解零售商优化问题的Kuhn Tucker条件，给出了非对称的生产成本扰动信息下的双渠道供应链的最优契约，并且分析了非对称成本扰动信息对于双渠道供应链定价决策、生产数量决策及供应链成员利润和整个系统性能的影响.研究表明，当生产成本扰动满足一定条件时，初始的生产计划仍然是最优的；制造商私有成本扰动信息不一定会给系统带来利润损失，并且明确给出了未造成利润损失的边界条件.

双渠道；扰动管理；非对称信息；委托代理理论；契约设计

经济全球化的加快产生了越来越多的具有相互依赖关系的企业，使供应链面对突发事件时更加脆弱［1］.事实也表明供应链越来越多地受到突发事件的干扰，如2011年日本9级大地震及随之发生的海啸摧毁了丰田公司在日本东北部的汽车零部件生产工厂，进而导致丰田公司不得不调整其在北美的生产计划.突发事件发生时，供应链受到不同层面、不同程度的影响，造成生产成本巨大波动，使原生产计划不再可行，若决策者不能及时地采取有效的策略加以应对，将会严重降低系统的性能.因此如何设计有效的契约来改善突发事件发生时供应链系统的性能以减少突发事件对系统绩效的不利影响对于供应链扰动管理有重要的理论价值和实践意义.

现有的关于供应链扰动管理的文献通常假定扰动信息是对称的，但在供应链实际运作中，扰动信息对于供应链成员来说通常是非对称的.例如，家乐福等大型零售商在我国市场上特别是国内一线城市居于强势地位，一些小品牌制造商为了更好地塑造其产品的品牌形象、开拓高端市场，争相与其签订采购合同［2］.但当突发事件发生导致签约制造商的生产成本扰动时，对强势零售商而言制定合理采购调整计划是一种挑战，因为生产成本扰动信息很可能是契约制造商的私有信息.因此非对称扰动信息下供应链决策问题在实际中较为普遍，近年来也成为国际管理界及委托代理理论的研究热点之一.

另外，由于网络销售渠道和传统销售渠道各自的特点，越来越多的企业纷纷将二者整合，从而形成双渠道销售模式.在双渠道供应链中，一方面供应商或制造商是零售商所售商品的供应者（零售渠道），另一方面供应商或制造商通过网络销售渠道（电子渠道）直接向消费者销售产品而成为零售商的直接竞争者，其双重身份的存在使得双渠道供应链的决策问题不同于传统零售渠道，因此，双渠道供应链的运作研究也引起了企业界和学术界的广泛关注.

国内外学者对双渠道供应链的研究已取得一些成果.Huang等［3-4］分别研究了需求扰动和生产成本扰动下双渠道供应链的定价和生产决策问题，但没有考虑突发事件下如何协调新的双渠道供应链系统.彭静等［5］研究了当突发事件发生仅导致需求发生扰动时制造商和零售商之间的竞争和协调问题.

以上研究主要针对信息对称的情形，在实际中，生产成本扰动信息通常只有制造商能够观察到，而零售商通常无法得到准确的该信息.由于生产成本扰动信息是非对称的情形非常普遍，所以假定制造商和零售商之间对于生产成本扰动信息是非对称的更能够反映实际情形.LEI等［6］在XU等［7］的基础上研究了在传统供应链中假设需求函数为线性函数，如何在非对称的需求扰动信息和成本扰动信息下设计最优的线性批发价格契约菜单问题.黄松等［8-9］在前述文献的基础上分别分析了需求扰动信息和生产成本扰动信息分别为零售商和供应商的私有信息时供应商和零售商应如何设计有效的契约菜单.

本文与文献［6］和［8］的不同之处在于：文献［6］和［8］的研究背景均为传统供应链环境（单一渠道），而本文考虑在双渠道供应链环境下，当突发事件发生导致制造商生产成本扰动且扰动信息为制造商私有信息时，零售商如何设计有效的契约菜单从而使制造商通过契约的选择揭示其真实类型，进而探讨非对称成本扰动信息对制造商、零售商及整个系统性能的影响.

1 常规下的双渠道供应链模型

考虑由单零售商（委托人）和单制造商（代理人）组成的双渠道供应链系统（如图1），假定制造商受零售商委托仅生产一种产品，其产品既可以批发价格w销售给零售商，零售商再以零售价格pr卖给终端消费者（零售渠道）；也可通过电子直销渠道以价格pd直接卖给终端消费者（电子渠道），不考虑库存.零售商决策目标是站在整个系统整体的角度使自己的利润最大，制造商决策目标是使自己的利润最大，与文献［6］的处理一致，本文设制造商的保留利润为零.设2种渠道的需求是关于价格的线性函数.

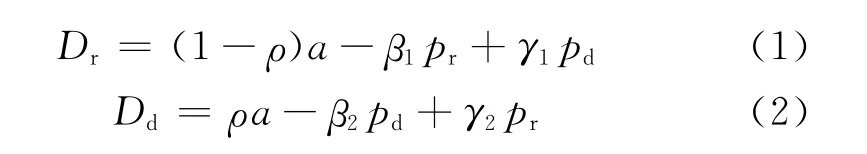
式中：下标r和d分别表示零售渠道和电子渠道；ρ为消费者对电子渠道的接受程度；a为市场需求规模；β1（β2）和γ1（γ2）分别表示零售渠道（电子渠道）的自有价格弹性系数和交叉价格弹性系数.为了便于分析，假设自有价格弹性系数和交叉价格弹性系数是对称的［8］（即β1＝β2＝β，γ1＝γ2＝γ），且β＞γ表明自有价格弹性系数大于交叉价格弹性系数.

图1 双渠道供应链系统Fig.1 Dual-channel supply chain system

当不存在生产成本扰动时，假设所有信息都是对称的.制造商和零售商都知道自己和对方的销售价格、成本结构和利润函数等.此时供应链系统的总利润函数为Π＝πr＋πm＝（pr-c）Dr＋（pd-c）Dd，其中πm和πr分别为制造商和零售商的利润，c为制造商生产成本的预测值.

在上述假设条件下，由文献［5］可知，当零售渠道的销售价格和电子渠道的销售价格分别为p＊r和p＊d时，系统的利润达到最大.此时零售渠道的销量（零售商的采购数量）和电子渠道的销量分别为D＊r和D＊d，因此制造商的最优生产数量为Q＊.

2 对称生产成本扰动信息下的最优决策

为了分析非对称的生产成本扰动信息对于双渠道供应链的决策和系统绩效的影响，首先分析当生产成本扰动信息是对称情形下的最优决策，以便为后续的分析提供比较基准.

对于常规下的双渠道供应链，因产品生产提前期较长，制造商已经根据c得到Q＊.然而安排生产计划后，当销售季节来临前突发事件发生了（如生产过程中机器故障、相关生产辅料价格的变化等），而突发事件导致制造商的生产成本发生变化，即新产品实际的生产成本为c＋Δc，其中Δc为生产过程中发生的成本扰动.当发生生产成本扰动时，为实现系统利润的最大化，双渠道供应链的生产数量和2个渠道的销售价格会发生变化.若生产成本扰动信息是对称的，此时零售商的决策最优化问题可表示为

式中：（x）＋表示max ｛0，x｝＋；θ1为当生产成本发生扰动后实际的产量大于原计划产量时（（Dr＋Dd）＞Q＊）时增加一单位生产所产生的额外成本；θ2为原计划产量大于实际产量时（Q＊＞（Dr＋Dd））的单位处理成本，并且假定max｛θ1，θ2｝＜c，制造商承担产量偏离的成本.约束条件为制造商获得的利润不小于其保留利润.容易看出，只有当约束条件为紧约束（取等号）时目标函数才可能实现最大化，否则w增加一个值ζ（ζ＞0），目标函数值会减小.将约束条件代入目标函数可得式（4）不是关于（pr，pd）的连续可微函数，因此需分（Dr＋Dd）≥Q＊和Q＊≥（Dr＋Dd）2种情况进行讨论.构造2种情形下双渠道供应链系统决策问题的拉格朗日函数，通过求解Kuhn Tucker条件可得到引理1，此部分求解较简单，故省略.

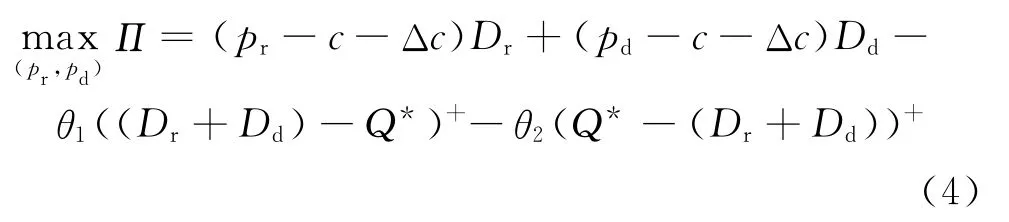
引理1当发生生产成本扰动Δc且扰动信息为制造商和零售商的共同知识时，双渠道供应链系统的最优定价和生产数量决策见表1，表中Q＊＊＝Dr＊＊＋Dd＊＊.

表1 对称生产成本扰动信息下双渠道供应链系统的最优定价和生产数量Tab.1 Optimal prices and production quantity under symmetric production cost disruption information in a dualchannel supply chain

3 非对称生产成本扰动信息下的契约设计

在供应链实际运作过程中，生产成本扰动信息通常是非对称的.当生产成本扰动信息是制造商私有信息时，零售商无法知道真实生产成本扰动信息，假定Δc∈｛ΔcH，ΔcL｝，系统中所有其他信息为双方共同知识.其中ΔcH（ΔcL）为高（低）的生产成本扰动值.设零售商虽不知道Δc的真实值，但知道Δc为ΔcH的概率是μ，为ΔcL的概率是1-μ.为表述方便，假定将观察到ΔcH的制造商为高成本制造商，而将观察到ΔcL的制造商为低成本制造商，且假定ΔcH＞ΔcL.当生产成本扰动信息为制造商私有信息时，为了实现系统利润的最大化，双渠道供应链2个渠道的需求量和销售价格将会发生变化.当制造商是高成本类型时，此时需求函数变为

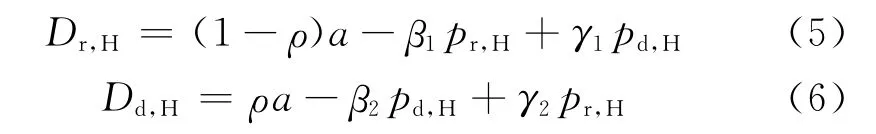
式中：pr，H，pd，H分别为当制造商为高成本类型时调整后的零售渠道价格和电子渠道价格.

当制造商是低成本类型时，此时需求函数变为

式中：pr，L，pd，L分别为当制造商为低成本类型时调整后的零售渠道价格和电子渠道价格.

零售商需要设计有效的契约来引导制造商通过契约选择来反映其所观测到的生产成本扰动类型.假定制造商（代理人）和零售商（委托人）之间的决策过程如下：①制造商观察到了实际的生产成本扰动ΔcH或者ΔcL；②零售商为高成本制造商提供契约（Dr，H，wH），为低成本制造商提供契约（Dr，L，wL）；③制造商根据其生产成本扰动类型或选择相应契约，或选择放弃；④一旦制造商选择了相应的契约，零售商必须按照契约规定的批发价格向制造商采购规定数量的产品.根据以上分析和假定，在非对称生产成本扰动信息条件下，零售商的决策优化问题表示为

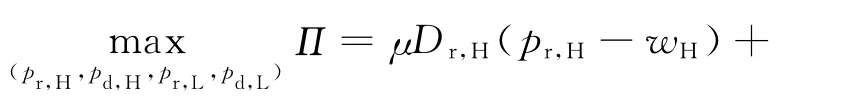
其中，不等式（10）和（11）表示激励相容约束，表明每种类型的制造商都没有动机去模仿其他类型制造商的契约选择，不等式（12）和（13）表示参与约束，表明只有当制造商获得的利润不低于其保留利润（文中假设为零）时才会选择相应的契约.

为求解式（9）至（13）所示的优化问题，做以下分析.显然，不等式（13）为冗余约束.在最优解处，不等式（11）和（12）必然是紧约束，否则零售商可以减少wH（wL）一个值ζ＞0，使得约束条件式（11）和（12）仍然成立，但是目标函数式（9）会增加，因此不等式（11）和（12）应取等号，即

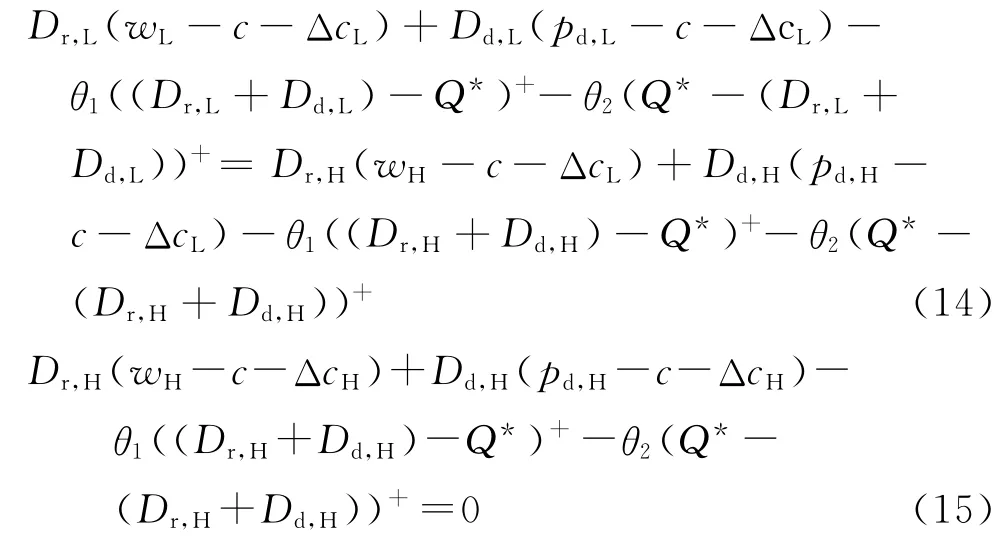
将式（14）和（15）合并化简可得

不等式（12）是紧约束，表明高成本制造商只能获得零利润，不等式（13）是松约束，表明低成本制造商能够获得正的信息租金，且信息租金为IR＝（Dr，H＋Dd，H）（ΔcH-ΔcL）.这表明在非对称生产成本扰动信息下，低成本制造商能够利用掌握生产成本扰动信息的优势获得正的利润，然而当生产成本扰动信息为双方共同知识时（对称信息情况下），制造商只能获得保留利润（文中假设为零）.

先不考虑式（11），将式（14）和（15）代入式（9），则零售商的最优化问题式（9）至（13）可以简化为

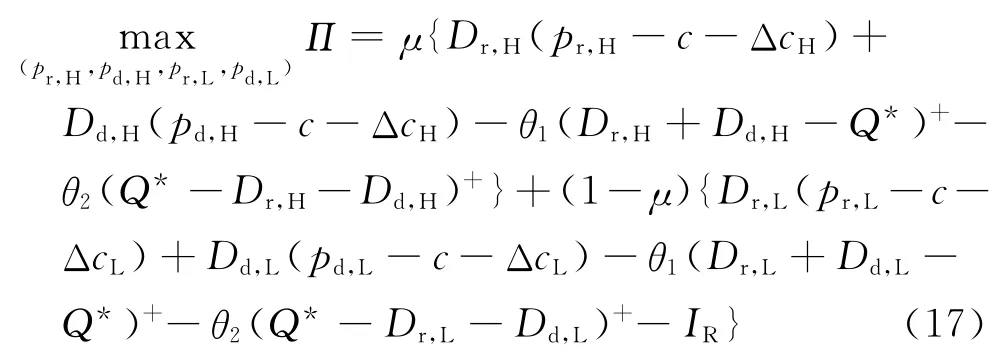
上述的最优化问题式（17）不是关于（pr，H，pd，H，pr，L，pd，L）的连续可微函数，因此需分Dr，H＋Dd，H≥Q＊，Dr，L＋Dd，L≥Q＊和Dr，H＋Dd，H≤Q＊，Dr，L＋Dd，L≤Q＊及Dr，H＋Dd，H≤Q＊，Dr，L＋Dd，L≥Q＊3种情况进行讨论.构造3种情形下双渠道供应链系统决策问题的拉格朗日函数，通过求解Kuhn Tucker条件可得到定理1.为表述方便，假设：

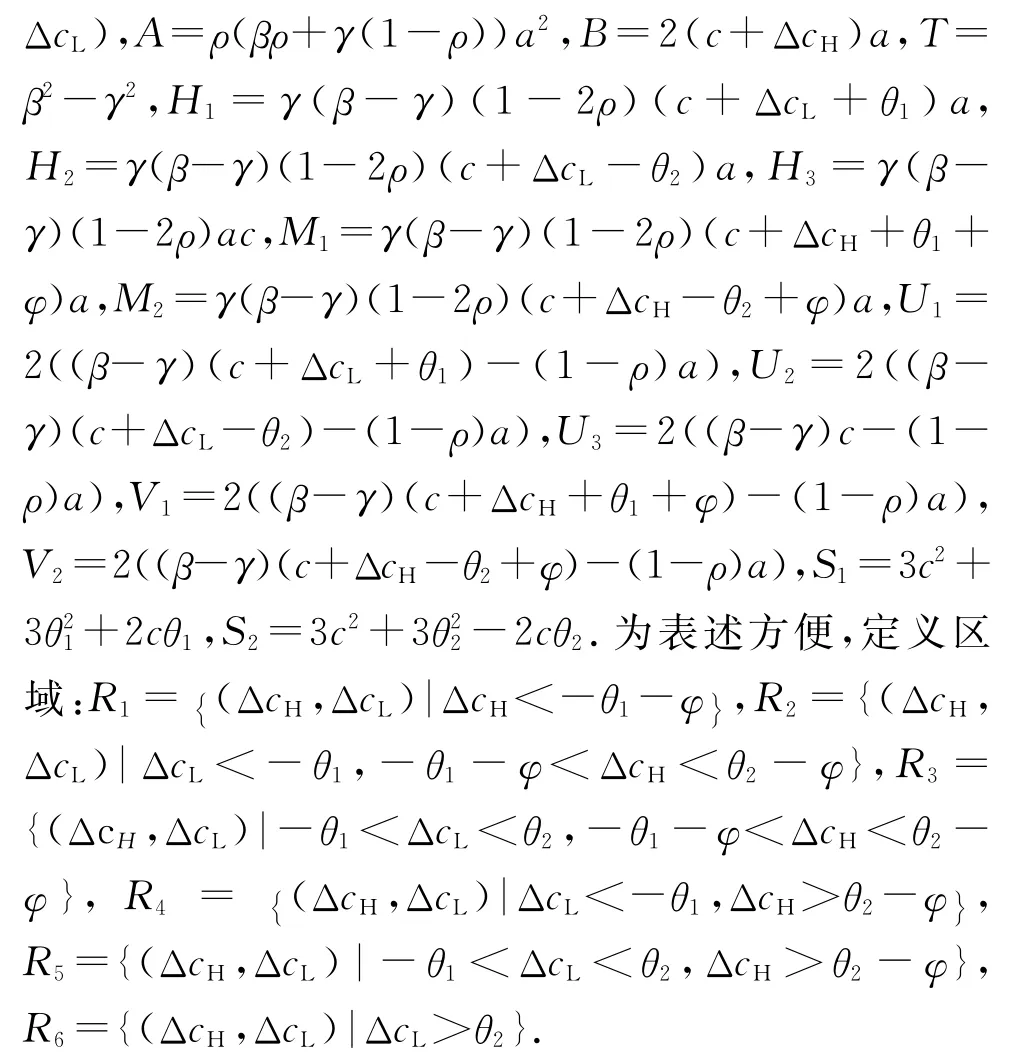
定理1当发生生产成本扰动Δc且扰动信息Δc为制造商私有信息时，此时双渠道供应链系统的最优生产和定价决策见表2和表3.

将定理1中的最优决策代入式（14）和（15）可求得wH，wL，定理2给出了非对称生产成本扰动信息下的最优契约菜单.

表2 生产成本扰动为ΔcH时最优定价和生产数量Tab.2 Optimal prices and production quantity when the cost disruption isΔcH

表3 生产成本扰动为ΔcL时最优定价和生产数量Tab.3 Optimal prices and production quantity when the cost disruption isΔcL

表4 生产成本扰动为ΔcH时的最优契约菜单Tab.4 Optimal contract menu when the cost disruption isΔcH

定理2给定生产成本扰动Δc，且扰动信息Δc是制造商的私有信息时，令｛（Dr，H，wH），（Dr，L，wL）｝为零售商在非对称的生产成本扰动信息下提供的最优契约菜单，则最优契约菜单见表4和表5.

注意到定理1中的6种情形必须满足ΔcH≥ΔcL，图2可将上述契约菜单中最优生产数量和生产成本扰动信息的关系直观地表示出来.如图2所示，对于低成本制造商，当ΔcL＜-θ1时（对应图2中区域R1，R2和R4），应增加生产数量；当-θ1≤ΔcL≤θ2时（对应图1中区域R3和R5），生产数量保持不变；当ΔcL≥θ2时（对应图2中区域R6），应减少生产数量.由进一步分析可知，在非对称生产成本扰动信息下，当零售商提供形如定理2中的契约菜单时，低成本制造商的生产决策与对称的生产成本扰动信息下的生产决策保持一致，换句话说，相对于对称的生产成本扰动信息，制造商私有生产成本扰动信息时，低成本制造商的生产数量没有发生扭曲.对于高成本制造商，当ΔcH＜-θ1-φ时（区域R1），应增加生产数量，当-θ1-φ≤ΔcH≤θ2-φ时（区域R2和R3），生产数量保持不变，当ΔcH≥θ2-φ时（区域R4，R5和R6），应减少生产数量.由进一步分析可知，一方面在非对称生产成本扰动信息下，当零售商提供形如定理2中的契约菜单时，对于高成本制造商扰动区间的端点分别由-θ1变为-θ1-φ，由θ2变为θ2-φ.另一方面，制造商私有生产成本扰动信息时，高成本制造商的生产数量小于或者等于相应区间的对称生产成本扰动信息下制造商的生产数量.换句话说，制造商私有生产成本扰动信息时，高成本制造商的生产数量发生了扭曲.

表5 生产成本扰动为ΔcL时的最优契约菜单Tab.5 Optimal contract menu when the cost disruption isΔcL

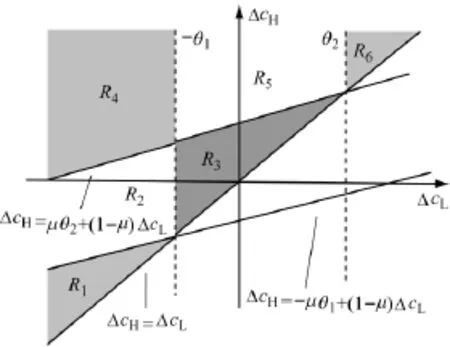
图2 非对称生产成本扰动信息下最优生产数量与生产成本扰动间的关系Fig.2 Optimal production quantity versus cost disruption under asymmetric production cost disruption information

通过比较引理1和定理1中的最优决策，可得如下推论.

推论1给定Δc，通过比较对称和非对称生产成本扰动信息下的最优决策可发现：

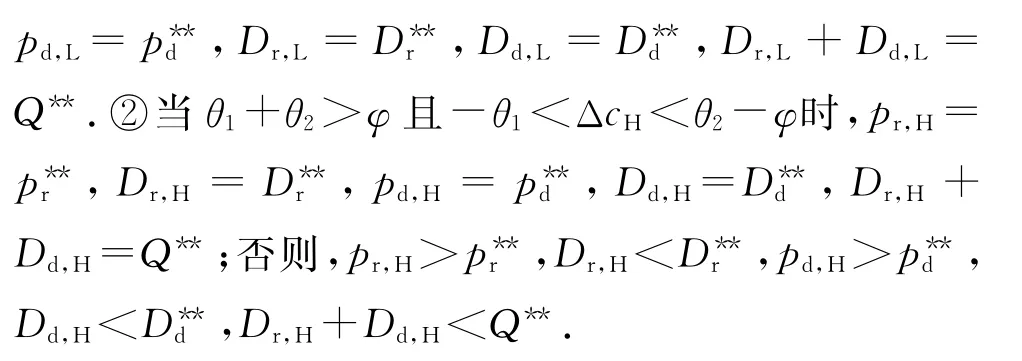
推论1表明非对称的成本扰动信息对双渠道供应链中定价和生产决策的影响.根据推论1，当制造商是低成本类型时，零售渠道和电子渠道的销售价格和数量与对称成本扰动信息下的相等，换句话说，当制造商是低成本类型时，非对称成本扰动信息对双渠道供应链的最优决策没有影响.当制造商是高成本类型时，仅当θ1＋θ2＞φ且-θ1＜ΔcH＜θ2-φ时，零售渠道和电子渠道的销售价格和数量与对称成本扰动信息下的相等，否则高成本制造商应降低生产数量（Dr，H＋Dd，H＜Q＊＊），增加2个渠道的销售价格才能实现系统利润的最大化.而高成本制造商生产数量的扭曲必然导致双渠道供应链系统的性能降低，下节给出具体的验证.

4 生产成本扰动信息的价值

信息价值是委托人在缺乏信息时的收益与拥有信息时所得的收益之差［8］.本文中信息价值为生产成本扰动信息对称与非对称下零售商（委托人）的收益之差值.当发生生产成本扰动并且成本扰动信息是零售商和制造商之间的共同知识时，零售商可以获得双渠道供应链系统的全部利润而制造商只能获得保留利润.然而在非对称生产成本扰动信息下，低成本的制造商可以从零售商那里得到一部分信息租金IR，以弥补其掌握扰动成本信息的优势，这同时意味着信息租金是系统内部成员间的利润分配，并没有造成整个系统利润的损失.而高成本的制造商依然只能获得保留利润.

根据推论1，信息不对称会使高成本制造商的生产数量发生扭曲，高成本制造商生产数量的降低必然会降低双渠道供应链系统的利润，换句话说，从双渠道供应链系统整体的角度来看，与对称成本扰动信息情况下相比，非对称成本扰动信息下的利润损失主要源于高成本制造商生产数量的扭曲.令ΔΠ表示双渠道供应链系统在对称与非对称生产成本扰动信息下的利润差异，于是ΔΠ＝Π（Q＊＊）-Π（QH），其中Π（QH）＝Dr，H（pr，H-c-ΔcH）＋Dd，H（pd，H-c-ΔcH）-θ1（（Dr，H＋Dd，H）-Q＊）＋-θ2（Q＊-（Dr，H＋Dd，H））＋.定理3给出了ΔcH在不同范围取值时的ΔΠ的值.

定理3假定高成本制造商观察到的生产成本扰动为ΔcH，则①当ΔcH＜-θ1-φ或者ΔcH＞θ2时，ΔΠ＝（β-γ）φ2／2；②当θ1＋θ2＜φ且-θ1-φ＜ΔcH＜θ2-φ时，或者当θ1＋θ2＞φ且-θ1-φ＜ΔcH＜-θ1时，ΔΠ＝（β-γ）（ΔcH＋θ1）2／2；③当θ1＋θ2＞φ且-θ1＜ΔcH＜θ2-φ时，ΔΠ＝0；④当θ1＋θ2＜φ且θ2-φ＜ΔcH＜-θ1时，ΔΠ＝（β-γ）（φ2＋（θ1＋θ2）（2ΔcH＋θ1-θ2））／2；⑤当θ1＋θ2＜φ且-θ1＜ΔcH＜θ2时，或者当θ1＋θ2＞φ且θ2-φ＜ΔcH＜θ2时，ΔΠ＝（β-γ）（φ2-（ΔcH-θ2）2）／2.

在情形①下，ΔcH＜-θ1-φ时，不论生产成本扰动信息是对称还是非对称，双渠道供应链的生产数量比扰动之前都应增加，而在非对称生产成本扰动信息下生产数量增加的量小于对称成本扰动信息下生产数量增加的量，从而造成整个双渠道供应链系统利润的损失（损失（β-γ）φ2／2）；ΔcH＞θ2时，不论生产成本扰动信息是对称还是非对称，双渠道供应链的生产数量比扰动之前都应减少，而在非对称生产成本扰动信息下生产数量减少的量大于对称成本扰动信息下生产数量减少的量，从而造成整个双渠道供应链系统利润的损失（损失（β-γ）φ2／2）.

而情形②至⑤下，可以发现θ2-φ和-θ1的大小关系对于生产成本扰动信息的价值具有重要影响，仅当θ1＋θ2＞φ且-θ1＜ΔcH＜θ2-φ时，对称生产成本扰动信息和非对称生产成本扰动信息下的系统的利润相等.换句话说，此时非对称生产成本扰动信息没有导致系统生产数量的扭曲，其他情况下均会导致生产数量不同程度的扭曲，进而导致系统利润不同程度的损失.

推论2如下：

（1）对于低成本制造商，有下面的不等式成立：πr，L＜π＊＊r，πm，L＞π＊＊m，πr，L＋πm，L＝π＊＊r＋π＊＊m.

（2）对于高成本制造商，有下面的不等式成立：πr，H≤π＊＊r，πm，H＝π＊＊m，πr，H＋πm，H≤π＊＊r＋π＊＊m，仅当θ1＋θ2＞φ且-θ1＜ΔcH＜θ2-φ时等号成立.

式中：π＊＊r，π＊＊m分别为对称生产成本扰动信息下零售商和制造商的利润.πr，L，πm，L分别为制造商私有生产成本扰动信息下当制造商为低成本类型时零售商和制造商的利润.πr，H，πm，H分别为制造商私有生产成本扰动信息下当制造商为高成本类型时零售商和制造商的利润.

在对称生产成本扰动信息下，零售商可获得系统的全部利润（π＊＊r＝Π），而制造商只能获得保留利润.而在非对称成本扰动信息下，当制造商是低成本类型时，双渠道供应链系统的生产数量没有发生扭曲，换句话说，系统的利润没有造成损失（πr，L＋πm，L＝π＊＊r＋π＊＊m），但从零售商的角度来看，零售商应支付一部分信息租金IR以补偿低成本制造商掌握信息的优势，因此πr，L＜Π，而低成本制造商获得的是信息租金，因此πm，L＝0.

当制造商是高成本类型时，制造商只能获得保留利润，零售商获得系统的全部利润，但此时双渠道供应链系统的生产数量发生不同程度的扭曲，进而造成系统利润不同程度的损失.因此当制造商是高成本类型时，零售商获得的利润小于对称成本扰动信息下系统的利润，即πr，H≤π＊＊r（仅当θ1＋θ2＞φ且-θ1＜ΔcH＜θ2-φ时，不等式取等号，即系统利润未造成损失），而此时πm，H＝π＊＊m＝0.

5 结语

研究了由一个制造商和一个零售商组成的双渠道供应链系统，制造商受零售商的委托仅生产一种产品，其产品既可以通过零售商也可以通过制造商自有电子直销渠道销售给消费者，当突发事件发生导致生产成本扰动并且扰动信息为制造商私有信息时零售商如何设计相应的契约来激励制造商接受契约进而最大化系统利润的问题.先给出了生产成本扰动信息为双方共同知识时系统的最优定价和生产决策，接着采用委托 代理理论，通过求解零售商优化问题的Kuhn Tucker条件给出了制造商私有生产成本扰动信息时的契约菜单，并计算出ΔcH在不同范围取值时信息的价值，分析了非对称成本扰动信息对系统最优定价和生产决策及供应链成员和系统性能的影响.

研究结果表明：当生产成本扰动信息为制造商私有信息时，仍然可以设计有效的契约菜单来改善双渠道供应链系统的性能；非对称成本扰动信息并非一定造成系统利润的损失，并明确给出了未造成利润损失的边界条件；当生产成本扰动信息为制造商私有信息并且制造商为低成本类型时，零售商通过设计有效的契约可以避免双渠道供应链系统利润的损失，但此时零售商的利润（系统利润）小于其对称情形下的利润，原因是需要支付给低成本制造商一部分信息租金以补偿其掌握成本扰动信息的优势；当生产成本扰动信息为制造商私有信息并且制造商为高成本类型时，零售商依然可以设计有效的契约来改善系统的性能，并明确给出了生产成本在不同扰动范围内的信息价值.

［1］ Adegoke Oke，Mohan Gopalakrishnan.Managing disruptions in

supply chains：A case study of a retail supply chain［J］.International Journal of Production Economics，2009，118（1）：168.

［2］ 田虹，袁海霞.与强势零售商合作的生存之道［J］，西部论丛，2010，10：72.TIAN Hong，YUAN Haixia.Surviving in cooperation with the dominant retailers［J］.Western Forum，2010，10：72.

［3］ Huang S，Yang C，Zhang X.Pricing and production decisions in dual-channel supply chains with demand disruptions［J］.Computers ＆Industrial Engineering，2012，62（1）：70.

［4］ Huang S，Yang C，Liu H.Pricing and production decisions in a dual-channel supply chain when production costs are disrupted［J］.Economic Modelling，2013，30（1）：521.

［5］ 彭静，林杰，林正.需求变动下双渠道供应链的竞争与协调［J］.同济大学学报：自然科学版，2015，43（1）：146.PENG Jing，LIN Jie，LIN Zheng.Competing and coordination strategies for dual-channel supply chain with demand disruption［J］.Journal of Tongji University：Natural Science，2015，43（1）：146.

［6］ LEI Dong，LI Jianbin，LIU Zhixue.Supply chain contracts under demand and cost disruptions with asymmetric information［J］.International Journal of Production Economics，2012，139（1）：116.

［7］ XU Minghui，QI Xiangtong，YU Gang，et al.Coordinating dyadic supply chains when production costs are disrupted［J］.IEE Transactions，2006，38（9）：765.

［8］ 黄松，杨超.非对称需求扰动信息下的供应链显示机制设计［J］.运筹与管理，2014，23（6）：116.HUANG Song，YANG Chao.Supply chain revelation mechanism design under asymmetric demand disruption information［J］.Operations Research and Management Science，2014，23（6）：116.

［9］ 黄松，杨超.非对称成本扰动信息非线性需求函数下的供应链契约设计［J］.中国管理科学，2014，22（8）：80.HUANG Song，YANG Chao.Contracting with asymmetric production cost disruption information under nonlinear demand function［J］.Chinese Journal of Management Science，2014，22（8）：80.

Contract Design with Asymmetric Production Cost Disruption Information in a Dual-channel Supply Chain

PENG Jing1，2，LIN Jie1，LIN Zheng3
（1.School of Economics and Management，Tongji University，Shanghai 200092，China；2.School of Information Engineering，Zhejiang Agriculture ＆Forestry University，Lin’an 311300，China；3.Zhejiang Provincial Special Equipment Inspection and Research Institute，Hangzhou 310020，China）

The contract design problem under asymmetric production cost disruption information in a dual-channel supply chain composed of one manufacturer and one retailer is investigated.By utilizing the principal-agent theory and solving the Kuhn-Tucker conditions of the optimization problem，the optimal contract under asymmetric production cost disruption information are derived.Moreover，the impact of asymmetric production cost disruption information on the dual-channel supply chain’s optimal pricing，the production quantity decision and supply chain members＇profit and the whole system performance of the dual channel supply chain are analyzed.It is found that the original production plan is still optimal under some specific conditions，asymmetric production cost disruption information does not necessarily cause profit loss for the system.And the conditions under which the asymmetric production cost disruption information will not cause profit loss to the system are also explicitly presented.

dual-channel；disruption management；asymmetric information；principal-agent theory；contract design

F252

A

0253-374X（2015）12-1915-08

10.11908／j.issn.0253-374x.2015.12.023

2015 02 09

国家自然科学基金（71071114，71302153）；中国博士后特别资助基金（2014T70838）

彭 静（1980—），女，讲师，博士生，主要研究方向为供应链管理.E-mail：zjpengqin@163.com