基于耦合矩阵修正和空间映射法的滤波器设计

张祎煊，殷新社，张 燚

（中国空间技术研究院 西安分院，陕西 西安 710100）

随着通讯技术不断发展，全波EM精确设计逐渐应用于很多滤波器设计中，但EM仿真的缺陷则在于仿真时间长，并且受计算资源的限制，不能进行很大范围的扫参运算。近些年来，Y参数提取技术的出现使问题得到很大的改善，Y参数提取[1]非常简单明了，寄生耦合位置、大小、符号等信息非常完整，滤波器的耦合矩阵可以从附加的虚拟端口直接提取出来[2]。Y参数提取在窄带滤波器设计中起到了非常重要的作用，甚至改变了现代滤波器设计的模式，提高微波滤波器的设计效率，并将成为今后滤波器精确设计的教程与标准。

本文基于多端口Y参数提取技术[3]，结合空间映射法[4-5]，提出了一种微波滤波器快速设计方法，用多端口Y参数提取而得的耦合矩阵作为初模型，HFSS13 EM仿真而得的耦合矩阵作为精细模型，进行迭代，且每一步迭代更新目标耦合矩阵，去除输入输出端口相位、寄生和色散；并利用HFSS13自带VB脚本功能编写调试程序，从而达到自动优化滤波器物理尺寸参数的目的。最后设计了一款六阶同轴滤波器，代入该程序迭代，6次迭代后仿真结果良好，证明了该方法的快捷有效。

1 空间映射法在腔体滤波器中的应用

分别单独改变D0中的尺寸一定步长，提取出相应的M矩阵，与预调尺寸提取的M矩阵做差，再与步长做比，就得到了M矩阵改变量与步长的差分。通过差分替代偏导就得出了SM矩阵。

SM矩阵、M矩阵差值与尺寸差值之间的关系为：

SM矩阵对角线元素不为零，因此是可逆的，求逆得出需要改变的尺寸的量：

其中 ΔMt=Mideal-M0t，Mideal为理想M矩阵写成的向量形式，M0t为预调尺寸提取出的M矩阵。

求解SM矩阵的过程中假定一个尺寸对应于多个M矩阵元素的影响是线性关系，显然这种线性关系在预调尺寸与最终尺寸越接近时线性度越好。如果通过（4）修改一次尺寸没有得到需要的结果，可以对修改后的尺寸再提取出M矩阵并用（4）计算第二次，此时SM矩阵不需要重新计算。

经过工程上具体编程实现发现，（1）式SM矩阵取逆后，通过（4）式得到的ΔD经常为仿真模型所不能达到的值，如调谐螺钉的负值等。这一是由于SM矩阵中Δmij与真实值之间有微小的差别，经过求逆运算将这种差别放大了；二是因为具体一个Δmij通常只与模型中一个ΔD0变量有关，而与其他变量ΔDx的关系不大，（1）式放大了这种关系。

工程调试程序时，可在SM矩阵每一个元素乘以权值kij，如下：

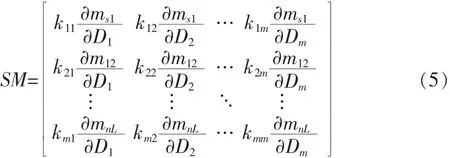
例如：假设对于 Δm12有直接关系的 ΔD2，给权重 k22=1，其他关系不大的ΔDx可视实际情况取0.1或者直接取0。

2 耦合矩阵的更新

文献[1]提出了谐振滤波器的耦合矩阵修正，在原有耦合矩阵公式的基础上，加入频率修正，使耦合矩阵的公式随频率而变化。公式如下：

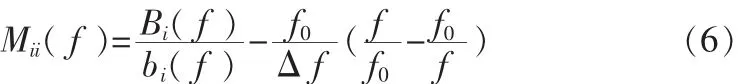
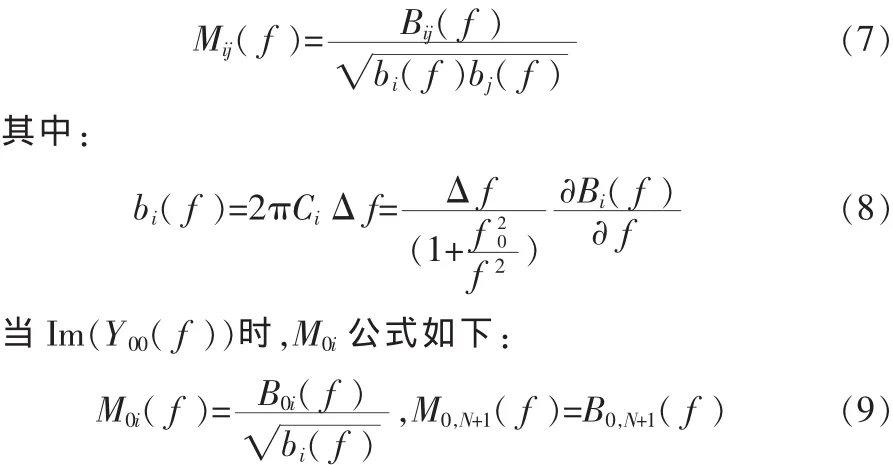
更新后的公式得出的S参数图像[8－9]与HFSS全波EM仿真得出的图像基本上完全重合，当所设计滤波器寄生耦合和色散严重时，目标耦合矩阵每迭代一次或多次需要更新，去除寄生耦合和色散的影响。目标耦合矩阵公式中可以清楚的看到寄生耦合，色散则由耦合矩阵随频率的变化在S参数图像的变化看出，将寄生耦合与色散加入目标矩阵，每几次迭代调节目标矩阵，使之达到设计要求。

运用更新后的耦合矩阵作为目标耦合矩阵来进行迭代，可以使滤波器设计更加准确有效。减少滤波器设计所需时间。

3 设计实例

用设计六阶同轴滤波器来验证此方法的有效性。技术指标为：

中心频率：1.693 GHz

带宽：60 MHz

带内回波损耗：20 dB

滤波器综合得，N+2矩阵为：

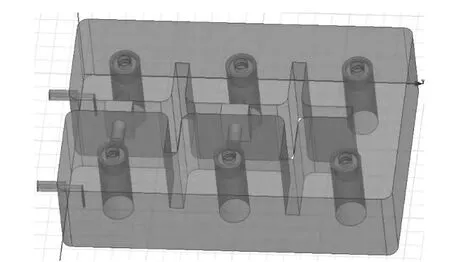
图1 六腔同轴滤波器Fig.1 The six－cavity coaxial filter

滤波器结构如图1，理想响应如图2，滤波器尺寸变化如表1。w12、w23和w34分别为12腔、23腔和34腔之间的耦合，w45=w23，w56=w12；Y_input为输入输出耦合；l16 和 l25为16腔和25腔之间的耦合；screw1至screw6为6个腔的调谐螺钉长度。初始长度为表一0次迭代。HFSS全波仿真后结果如图3～6所示。

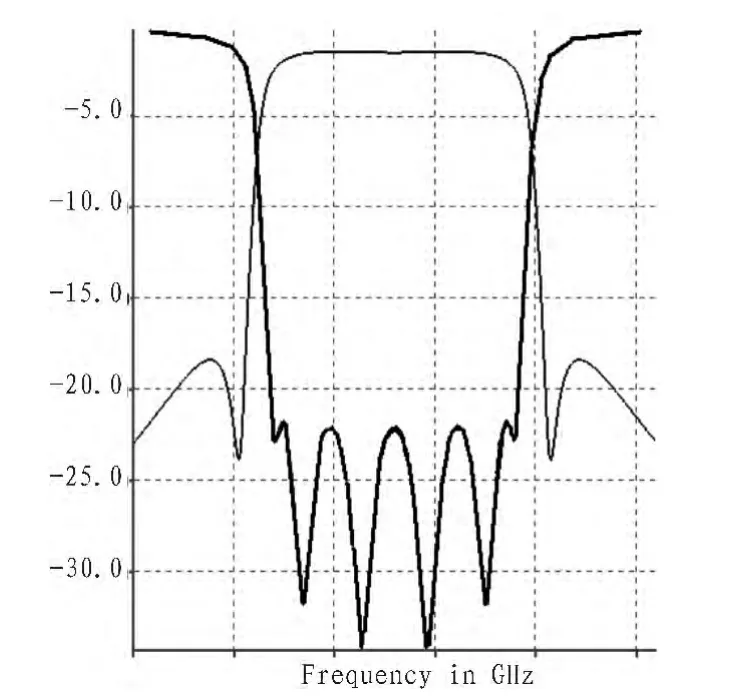
图2 理想曲线图像Fig.2 Ideal S11 and S21

图7 图8可以清楚的看出，多端口Y参数提取的矩阵经过修正后，得出的S参数图像与HFSS全波仿真在带内完全吻合，因此每次迭代完全可以用多端口Y参数提出的矩阵代 替其实际响应，从而加快滤波器设计速度。

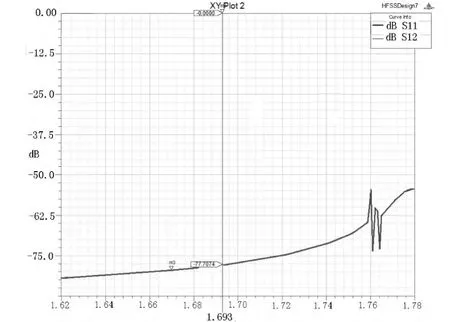
图3 初值时S参数图Fig.3 S11 and S21 in initial value

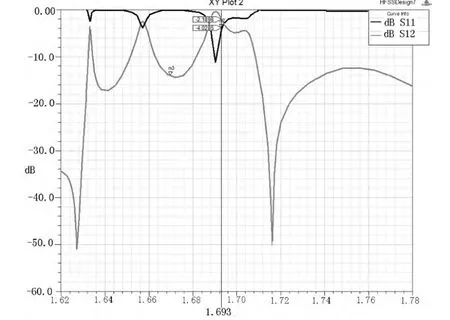
图4 迭代1次时S参数Fig.4 S11 and S21 on the first iteration

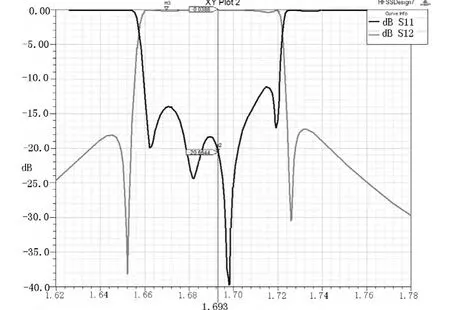
图5 迭代4次时S参数图Fig.5 S11 and S21 on the forth iteration

表1 迭代过程中滤波器的尺寸变化Tab.1 The physical size of microwave filters in every iterations

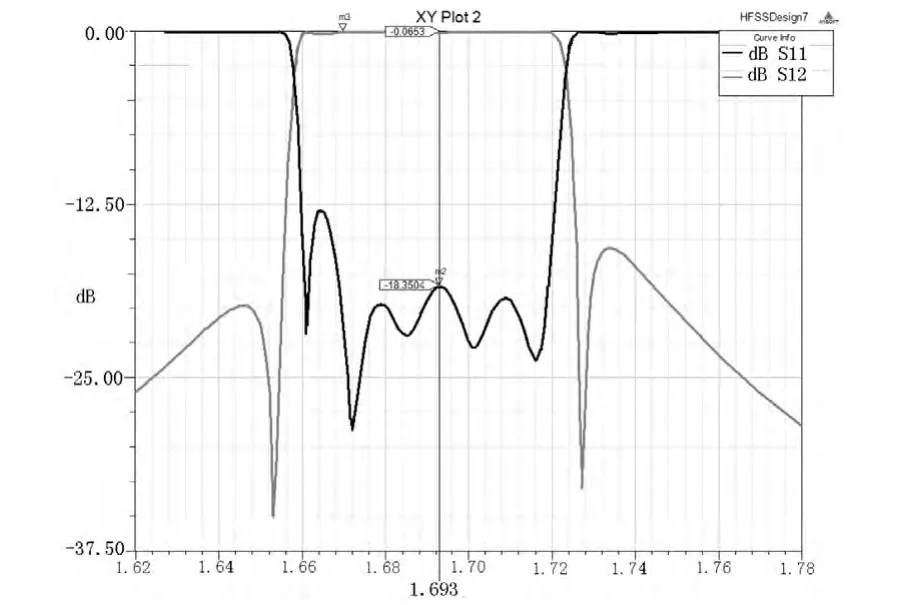
图6 迭代6次时S参数Fig.6 S11 and S21 on the sixth iteration

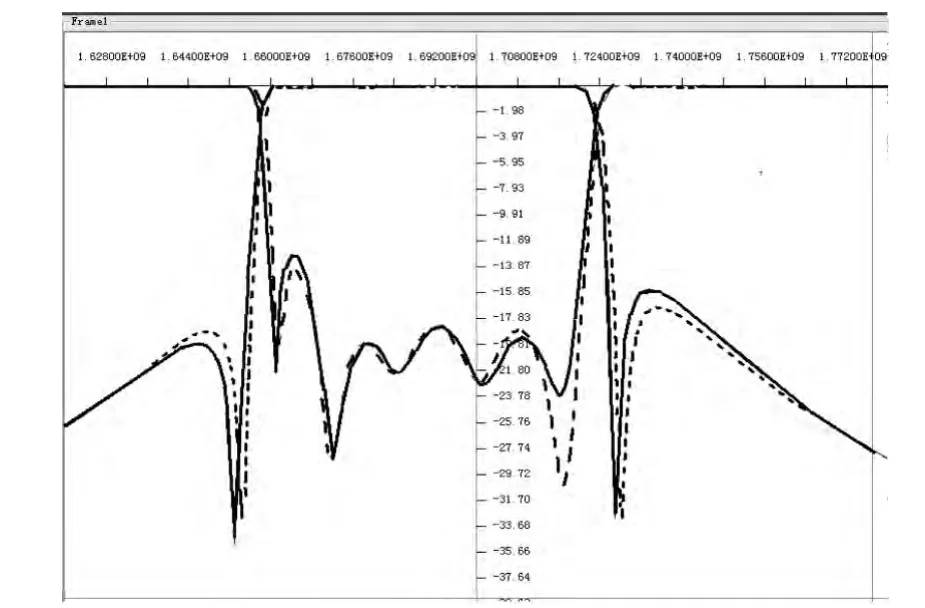
图7 实线为HFSS仿真；虚线为多端口Y参数提取Fig.7 HFSSsimulated results and CM extracted response

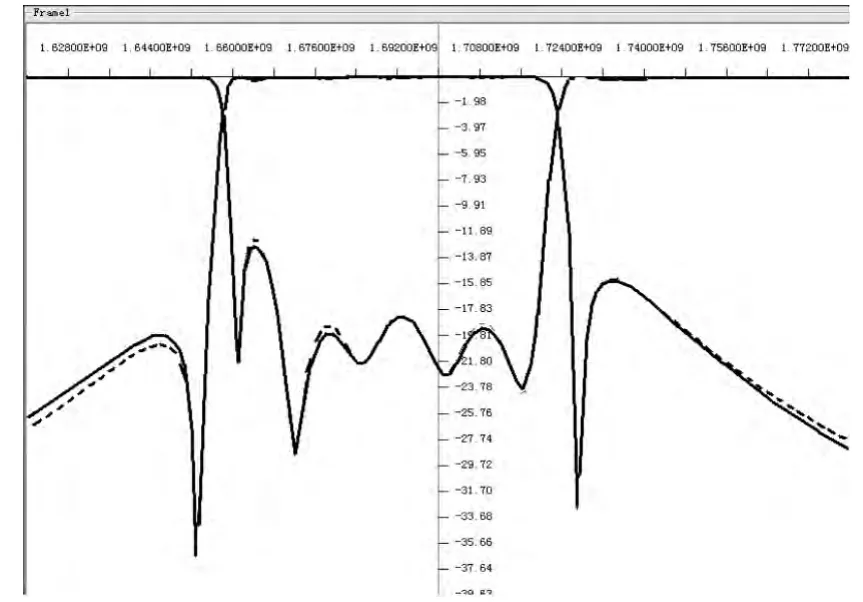
图8 虚线为修正耦合矩阵后多端口Y参数提取Fig.8 HFSSsimulated results and accurate CM

初始值的选取为范围内随意给出，取整即可，并不要求精度，表一可发现耦合参数很快迭代到合适参数附近，频率参数则左右摇摆于合适值附近，6次迭代后物理尺寸改变已然不大。由图可见其初值时滤波器响应并不理想，6次之后响应向右偏移，不过已经很好，结果调入Ansoftdesigner，协同仿真即可。

本文所述方法需要拟定ΔD，ΔD可选择D取值范围的10%-20%即可，为方便，该设计十二个尺寸值步长均取0.5 mm，带入自编程序，一次迭代后采取更新SM矩阵，由更新后的SM矩阵计算出ΔD，滤除坏值，6次迭代后结果如图6所示。

4 结束语

文中提出了一种微波滤波器快速设计方法并作出了改进，该方法适用于大部分应用多端口Y参数提取的微波滤波器的设计，并可用来辅助设计双工器、多工器。本方法对初始尺寸增加微扰量，进行一次全波仿真即可计算出SM矩阵，并且应用HFSS自带脚本系统自动完成其余仿真，期间几次迭代后需要人为更新目标矩阵，可以减少迭代次数，快速达到设计曲线要求。最后设计了一款六阶同轴滤波器，经6次迭代后得到理想响应对应的最佳尺寸，证明了此方法的正确性。该方法在工程设计中具有普适性和便捷性，有很大的应用前景。

[1]Yin X.Accurate extraction of coupling matrix for coupled resonator filters[C]//Microwave Symposium Digest （MTT），2012 IEEE MTT-SInternational.IEEE，2012:1-3.

[2]Edquist A.Filter design and Ansoft tools[J].HFSSInfo Day，Stockholm， Sweden，2009.

[3]殷新社.Y参数提取在微波滤波器与多工器中的应用[R]航天五院西安分院，2011.

[4]Cameron R J，Yu M.Design of manifold-coupled multiplexers[J].Microwave Magazine， IEEE，2007，8（5）:46-59.

[5]Ismail M A，Smith D，Panariello A，et al.EM-based design of large-scale dielectric-resonator filters and multiplexers by space mapping[J].Microwave Theory and Techniques，IEEE Transactions on，2004，52（1）:386-392.

[6]陈建忠，梁昌洪，陈佳，等.基于参数提取和空间映射的滤波器优化设计 [J].华南理工大学学报:自然科学版，2011，39（10）:32-37.CHEN Jian-zhong，LIANG Chang-hong，CHEN Jia，et al.Optimization design of filters based on parameter extraction and space mapping[J].Journal of South China University of Technology:Natural Science Edition，2011，39（10）:32-37.

[7]张燚.侧壁耦合输出多工器设计仿真技术研究[D].西安：中国空间技术研究院西安分院，2010.

[8]Cameron R J，Kudsia C M，Mansour R R.Microwave filters for communication systems[M].Wiley-Interscience，2007.

[9]Cameron R J.General coupling matrix synthesis methods for Chebyshev filtering functions[J].Microwave Theory and Techniques， IEEE Transactions on，1999，47（4）:433-442.