基于蚁群算法的配送网络拓扑图设计与研究

毕洪山，何光营，韩 印

(1.上海理工大学 管理学院，上海 200093;2.上海电力学院 现代教育技术中心，上海 200090;

3，上海理工大学 交通系统工程研究所，上海 200093)

配送网络是物流系统的核心环节，直接影响物流的效率.[1-2]配送网络规划是指根据投资及运行费用等约束条件，在已有设施和线路的基础上，针对新的配送客户出现的情况进行搜索的一种配送方案，目的是在满足相关的其他约束条件和可靠性要求的同时，使配送网络建设投资的费用和相关的运行费用最小.这种搜索本质上是一个复杂的优化组合问题.科研人员已经研究了很多智能算法，如遗传算法、人工神经网络粒子群算法等，本文提出了一种基于改进的蚁群算法来求解配送网络扩展优化问题的数学模型，并设计了相应的求解算法.

1 配送网络拓扑图的数学模型

配送网络的数学模型直接影响车辆路径的求解.[3]在此模型中，设定参数约束车辆的载重和行驶的路线长度，并不涉及货物的类型.车辆路径规划问题是一个NP完全的问题，该问题可以看作是旅行商问题(Traveling Salesman Problem，TSP)和装箱问题(Bin Packing Problem)的复合问题.

本文提出多目标数学模型.设某配送中心(Distribution Center，DC)可以调度的车辆为T:

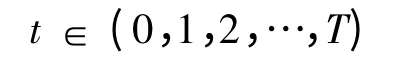
配送中心要服务的客户群为P:

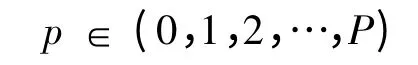
当p=0时表示车辆在配送中心.每辆车的载重为B，bt即为t车的载重.客户群P中每个客户的需求为 D，dp即为客户 p的需求.客户间的运输成本为C，cij即为从客户i到到客户j的运输成本.模型建立后，优化的结果要满足调度车辆最少和行车路线最短.为此定义参数xit，yijt且满足:

配送网络的数学模型为:

客户需求为D，要求每个客户必须都被服务到，即:

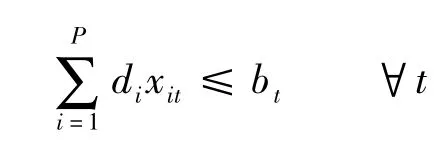
此时参数xit满足:

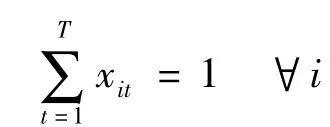
此时再考察参数yijt，有:

参数xit和yijt考察完毕后就可以保证客户仅被一辆车访问.

计算中产生的子回路必须消除，堵子回路采用如下公式:

参数取值满足如下条件:

2 蚁群算法及其实现

2.1 蚁群算法简介

蚁群算法(Ant Colony Optimization，ACO)是一种用来在图中寻找优化路径的概率型算法.[4-7]经过长时间的观察发现，在寻找食物的过程中，蚁群群体搜索食物源路径的行为有很强的智能性.

蚁群算法是一种模拟进化算法，初步研究表明，该算法对群体智能搜索最短路径问题有很强的指导性.

针对大群体多参数优化路径设计的问题，将蚁群算法的设计结果与相应遗传算法的设计结果进行对比，通过数值仿真结果表明，蚁群算法是一种新型的模拟进化优化方法.

蚂蚁最初寻找食物时的路线图如图1所示.

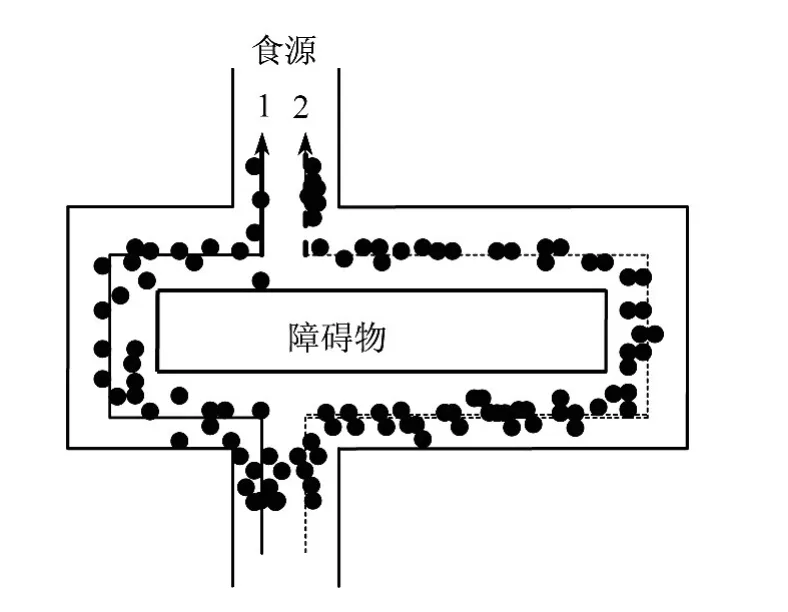
图1 蚂蚁开始寻找食物时的路线

蚁群在路径1和路径2上对等分布，当某个蚂蚁发现食物源后，它能在其走过的路径上留下一种蚁群所特有的分泌物质，即为信息素，而其他蚂蚁在移动的过程中能够感知到这种信息素的存在及其浓度，并以此修正自己前进的方向，大量的蚂蚁倾向于向信息素浓度强的方向前进.长时间后由大量蚂蚁组成的蚁群的群体行为便呈现一种信息素正反馈的现象，即某一路径上走过的蚂蚁越多，那么后来者选择该路径的概率就越大，如图2所示.

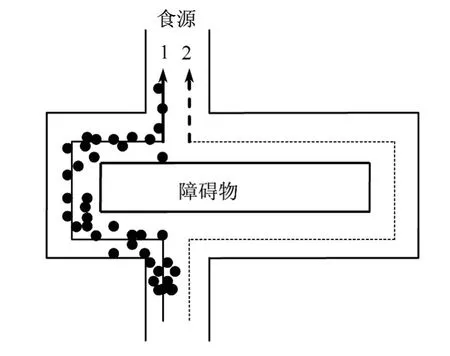
图2 蚂蚁发现最短路径后的路线

2.2 蚁群算法的实现

假设有m只蚂蚁，有n个随机选择的城市，m只蚂蚁要遍历 n个城市.[8-10]那么每一只蚂蚁 a的每一步行动b必须依据某个函数选择下一个没有到过的城市节点，同时在完成某一步或者整个循环后，立刻更新所有经过的路径上的残留信息素浓度.

根据以上原理构建转移函数，根据转移函数的概率选择下一个城市节点，在t时刻城市i和城市j间的路径上残留信息素浓度为Sij(t)，即由算法本身提供的信息.由城市i转移到城市j的启发信息素为Gij，该启发信息素由目标函数给出，由设定的算法实现.那么某时刻位于城市i的蚂蚁a选择城市j为目标城市的概率为Pij(a).

同时，为了避免对同一城市节点的重复访问，每只蚂蚁必须保存一个列表t(k)，用于记录到目前为止已经访问过的城市.在某一只蚂蚁完成对所有城市的访问后，算法必须对残留信息素进行更新处理，减小旧的信息素，同时加入蚂蚁访问路径留下的最新的信息素Sij(t).

3 应用蚁群算法设计配送网络

3.1 定义配送网络中的蚂蚁

(1)每只蚂蚁随机分布在不同的源结点，且能够独立地寻找从源结点到目的结点的较优路径，不同蚂蚁之间是并行的.[11]

(2)蚂蚁之间通过GPS定位系统给配送中心反馈实时路况信息素，配送中心再将此信息素放送给蚂蚁.以此方式间接完成蚂蚁之间信息素的传递.

(3)路径上共有 n个结点，蚂蚁经过该路径时释放的信息素平均分配在这n个结点上.

(4)在行驶过程中，蚂蚁收集的信息包括行驶时间长度、路况信息、恶劣路况等，由配送中心做出标记.

(5)蚂蚁到达目的结点后必须沿着同样的路径返回源结点.用蚂蚁一个来回所花费的代价的倒数作为信息素，并将该信息素值平均分配在该路径的所有结点上.

(6)蚂蚁返回源结点后配送中心即删除该蚂蚁.

3.2 改进蚁群算法的转移概率

t时刻位于城市i的蚂蚁a选择城市j为目标城市的概率是Pij(a)，路径上信息素浓度为:

αij(t+m)= βαij(t)+Sαij(t+m)得出转移概率为:

从i和j的积中取得n个数，目的是为加强下一节点的概率计算，减小选择下一节点的盲目性.根据信息素浓度确定出蚂蚁从该节点到其相邻节点的转移概率，并取得转移概率的最大值运动到下一个节点.

随着时间的推移，所有蚂蚁因线路长度或退化而不再向前运动.计算每个蚂蚁所花费的时间和成本，取满足约束条件的线路费用最小的一条作为配送网络优化后的第一条线路，然后将第一条线路信息通过GPS系统发送到终端，修改它们的轨迹，让蚂蚁转移到线路一.重新调用蚂蚁算法修正线路一.线路一随时间进化为最优线路.

4 配送网络的系统流程及编程

4.1 系统流程

整个配送网络系统设计总体流程为:首先设定算法的参数，再比较各条配送线路的长度，通过转移概率取得下一个配送节点.[12]详细流程如图3所示.

4.2 C语言实现配送网络

系统实现的核心伪码表示如下:

double d_xxs=1//初始信息量的多少

double d_ljxxs[][]//每条路径上的信息量

double d_ljxxs[][]//代表对应路径上的信息素增量

double d_city[][]//城市距离矩阵

double f_qf[][]//启发函数其值

f_qf[i][j]=1/d_city[i][j]

int i_no[][]//i_no[a][b]=1 表示蚂蚁 a已经走过了b城市

int ant[][]//蚂蚁 a 的路径的数组为 ant[a][]

double d_solu[];

int i_br[];

double qfyz，qwqfyz，ssxcl，e.

图3 蚁群算法流程示意

Pija(t)表示t时刻蚂蚁a由城市i转移到城市j的状态转移概率;qfyz代表信息素启发因子，表示某路径的相对重要性，可以真实地反映蚂蚁在移动过程中所积累的信息素在其他蚂蚁运动时所起的指导作用，其值越大，则蚂蚁越倾向于选择其他蚂蚁经过的路径，这样就加强了蚂蚁间的协作性;qwqfyz代表期望的启发式参数，表示路径能见度的相对重要性，其真实反映了蚂蚁在运动过程中启发信息是在其他蚂蚁选择路径时受到重视程度的大小，其值越大，转移概率贪心性越强;ssxcl代表信息残留因子;e代表信息素强度，用于计算蚂蚁留在路径上的信息量;int num表示迭代次数的运行费用和可靠性.

根据概率函数计算蚂蚁的转移概率的函数如下:

程序中输入不同的节点数坐标，得到的实验数据如表1所示.

表1中，l为配送完相应节点的总路径长度，t为配送完相应节点的总行驶时间，不记录在客户处停留的时间.

从表1可以看出，节点数越多，改进后的蚁群算法的优势越明显，即大型配送系统更适合该改进后的蚁群算法.

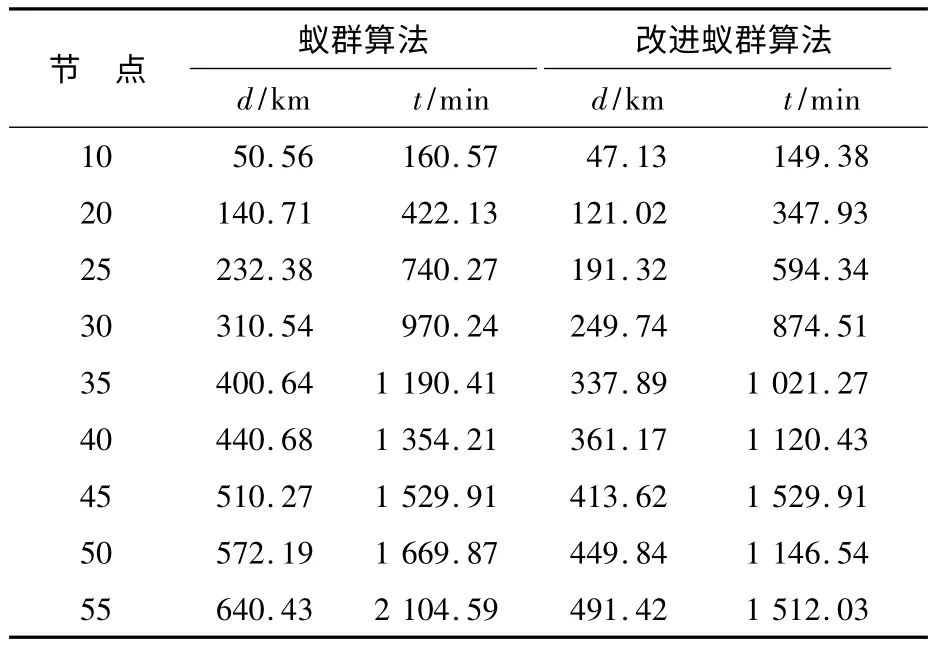
表1 蚁群算法的实验数据

5 结语

本文将蚁群算法应用于配送网络拓扑图设计中.以运行费用和行车时间之和为目标函数，建立了相应的求解算法.改进了蚁群算法的转移概率，在对可行性解空间进行搜索时提高了效率，加速了收敛.最后通过C语言实现了算法.实验结果表明，本文提出的基于蚁群算法的配送网络拓扑图在最短路径搜索上是可行的.

[1]马向国.现代物流配送中心规划、仿真及应用案例[M].北京:中国发展出版社，2014:10-126.

[2]李珍萍，周文峰.物流配送中心选址与路径优化问题——建模与求解[M].北京:机械工业出版社，2014:200-260.

[3]赵燕伟，张景玲，王万良.物流配送的车辆路径优化方法[M].北京:科学出版社，2014:60-80.

[4]李丽香，彭海朋，杨义先.混沌蚁群算法及应用[M].北京:中国科学技术出版社，2013:100-190.

[5]马良，朱刚，宁爱兵.蚁群优化算法[M].北京:科学出版社，2008:15-160.

[6]邱铁.蚁群算法及其应用[M].哈尔滨:哈尔滨工业大学出版社，2004:50-141.

[7]钱洁，郑建国.网络化制造模式下基于改进蚁群算法的供应链调度优化研究[J].系统工程理论与实践，2014，34(5):1 267-1 275.

[8]杨信廷，钱建平，范蓓蕾，等.农产品物流过程追溯中的智能配送系统[J].农业机械学报，2011，42(5):125-130.

[9]蔡延光，张敏捷，蔡颢，等.基于蚁群优化算法的同构多核任务分配与调度[J].江苏大学学报:自然科学版，2014，35(6):679-684.

[10]王跃岗，车阿大.基于相邻交换复合蚁群算法的多产品供应链调度优化[J].计算机集成制造系统，2014，20(5):1 171-1 180.

[11]史恩秀，陈敏敏，李俊，等.基于蚁群算法的移动机器人全局路径规划方法研究[J].农业机械学报，2014，45(6):53-57.

[12]张景玲，赵燕伟，王海燕，等.多车型动态需求车辆路径问题建模及优化[J].计算机集成制造系统，2010，16(3):543-550.