电力系统中长期负荷预测改进算法分析

潘雪涛

(上海电力学院 电气工程学院，上海 200090)

中长期电力负荷预测是城市电网规划中的基础性工作，其预测精度会直接影响到城市电网规划的质量.最小二乘支持向量机(Least Square Support Vector Machine，LS-SVM)是标准支持向量机的一种扩展，它是支持向量机在二次损失函数下的一种形式.LS-SVM只需求解线性方程，计算速度快，可以较好地解决小样本、非线性、高维数和局部最小点等实际问题，目前已成功应用于许多电力系统负荷预测的研究中.文献[1]至文献[4]将支持向量机和聚类算法相结合，以改善支持向量机在短期负荷预测中的应用效果.文献[5]至文献[8]将LS-SVM 成功用于短期负荷预测回归算法.但LS-SVM的预测精度在很大程度上依赖于训练集样本的规律性，因此本文采用粒子群优化改进最小二乘支持向量机算法，利用寻优算法来选择其权重参数，以提高预测精度.

1 LS-SVM原理

LS-SVM 是于 1999年由 SUYKENS等人[8]提出的.与基本SVM算法的主要区别在于:LSSVM可采用不同的优化目标函数，并用等式约束替代不等式约束，将支持向量机中求解二次规划问题转化为求解线性方程组问题，因而极大地简化了计算，提高了收敛速度.具体推导过程如下.

训练样本集{(x1，y1)，…，(xl，yl)}⊂Rn× R，其中xi为第i个n维输入，yi为输出.设线性回归函数为:

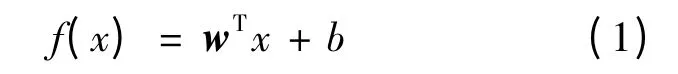
式中:w——权向量，w∈Rk;

b——常数，b∈R.

为了增加SVM的鲁棒性，采用损失函数引入结构风险，损失函数的表达式为:

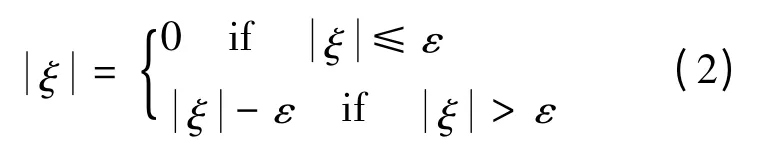
将回归问题转化为二次优化问题:

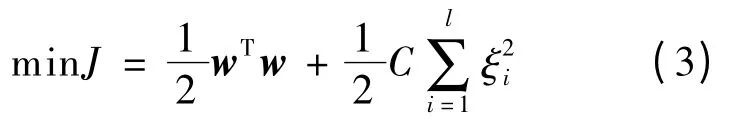
约束条件为:

根据目标函数和约束条件建立拉格朗日函数，然后根据库恩-塔克(KKT)条件分别对自变量求偏导，消去变量w和ξ可得线性系统如下:

式中:lv=[1，…，1]T;

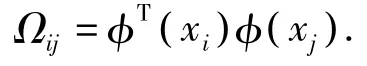
用最小二乘法求解上面的线性方程组得到a和b，则负荷预测回归函数为:

本文取RBF核函数为:

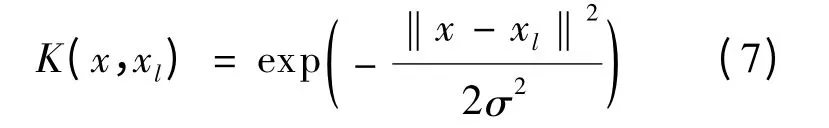
由此可见LS-SVM的函数估计精度和收敛速度受(C，σ)选择的影响.

2 粒子群优化算法

粒子群优化算法(Particle Swarm Optimization，PSO)广泛应用于很多工程问题的优化分析.[9-10]考虑到D变量的优化问题，一个 N粒子群的初始化是每个粒子分配到D维超空间内的随机位置.在此空间内用x表示一个粒子的位置，v表示一个粒子的飞行速度.x和v均为n×d矩阵，n为粒子个数，d为解空间维数.

一个粒子最佳的通过位置是Pbest.在粒子群中最佳粒子的指数是Gbest.找到这两个极值后，每个粒子的速度和位置按如下原则更新.

式中:ω——惯性权重量;

ρ1，ρ2——随机变量，ρ1= τ1C1，ρ2= τ2C2，C1和C2为正加速度常数.

惯性权重量ω的计算式为:

式中:ωmax，ωmin——最初和最后的惯性权重量，是惯性的最大值;

τ——当前的惯性值.

粒子的飞行速度有一个最大值vmax，用于限制粒子的飞行速度，通过调整 ω，vmax可以达到POS的最佳寻优能力.粒子会根据自身的适应度调整位置，最终聚积在最优值附近.

3 基于PSO的LS-SVM参数优化改进

利用PSO进行参数优化，模型的输入和输出层分别有6个输入节点和1个输出节点.选取20组样本数据，其中16组作为训练样本，4组作为验证样本，以验证模型的正确性.对数据进行归一化处理到[0，1]，在 Matlab 2009支持 LSSVMlab1.5工具包里，正规化参数和径向基核参数分别为 gam=100，sig2=0.7.具体步骤如下:

(1)对历史负荷数据进行归一化处理.

(2)选择预测年份前一年，以及利用相似搜索求出的与预测前一年相似的17组数据进行训练.

(3)选取核函数和参数，利用LS-SVM对其进行训练.

(4)利用训练好的LS-SVM负荷预测模型得出预测相点，对预测相点进行还原，得出预测负荷.

(5)计算百分比误差(MAPE)，[11]该误差也是PSO算法中粒子的适应度函数，计算公式为:

N——预测点总数.

(6)采用 PSO寻优，种群规模取为20，实数编码.PSO取全局模式，学习因子 C1=C2=2.0，初始惯性权重 ωmax=0.9，最后惯性权重 ωmin=0.2，算法中止条件为迭代次数100次.

(7)使用PSO找到的参数提取LS-SVM的输出值.

(8)再次用LS-SVM进行预测，最后的输出值反映了基于粒子群优化的负荷预测.

4 算例分析

电力需求的变化受到诸多因素的影响.本文采用6个输入和1个输出的模型，对某省年用电量进行预测.考虑经济、人口、气候和电价作为影响因素，采集1990～2009年该省的年用电量作为样本，输入参数取GDP(亿元)、人口数(万人)、全社会用电量(亿kWh)、综合电价(元/kWh)、冬季平均气温(℃)、夏季平均气温(℃)等6个变量.

利用1990～2005年的数据训练该模型后，对2006～2009年测试集数据进行预测.以该地区供电量为例，运用上述方法进行供电总量的预测，并将预测结果与其他几种预测方法进行分析和比较，如表1和表2所示.

由表1和表2可知，采用粒子群优化的算法在泛化能力、收敛速度以及搜索全局最优解方面都具有优势.其训练集样本平均相对误差为0.26%，验证样本平均相对误差为0.76%，均小于其他两种预测方法，且模型的验证样本输出值与实测值十分接近.在收敛速度方面，基于PSO的LS-SVM 算法平均运算时间为0.534 654 s，较LS-SVM算法稍有提高.在给定初始参数后，改进算法每次训练都可以得到相近的结果，这说明得到的是全局最优解.因此，算例分析证明了本文提出的混合算法的合理性和优越性.

表1 3种预测方法的负荷预测结果比较 106kWh

表2 3种预测方法的负荷预测结果相对误差比较 106kWh

5 结语

本文通过算例分析验证了基于PSO算法改进的LS-SVM的中长期负荷预测方法可以提高负荷预测的精度.后续的研究还可以对输入参数进行敏感性分析，进一步优化数据结构，提高负荷预测的准确性.

[1]李林峰，孙长银.基于FCM聚类与SVM的电力系统短期负荷预测[J].江苏电机工程，2007，26(3):47-50.

[2]姜惠兰，刘晓津，关颖.基于硬C均值聚类算法和支持向量机的电力系统短期负荷预测[J].电网技术，2006，30(8):81-85.

[3]张怡，张峰.电力系统超短期负荷预测技术的应用与发展[J].浙江电力，2010(2):5-8.

[4]钱虹，阮大兵，黄正润.电力系统超短期负荷预测算法及应用[J].上海电力学院学报，2013，29(1):9-12

[5]杨延西，刘丁.基于小波变换和最小二乘支持向量机的短期电力负荷预测[J].电网技术，2005，29(13):60-64.

[6]WU H S，CHANG X L.Power load forecasting with least squares support vector machines and chaos theory[C].The Sixth World Congress on Intelligent Control and Automation，2006:4 369-4 373.

[7]刘学琴，吴耀华，崔宝华.基于扩展粗糙集的短期电力负荷预测模型[J].电力系统保护与控制，2010，38(5):11-15.

[8]邓乃扬，田英杰.数据挖掘中的新方法——支持向量机[M].北京:科学出版社，2004:235-247.

[9]ABIDO M A.Optimal power flow using particle Swarm optimization[J].Electrical Power and Energy System，2002，24(7):563-571.

[10]YOSHIDA H，KAWAM K，FUKUYAMA Y，et a1.A particle swarm optimization for reactive power and voltage control considering voltage security assessment[J]. IEEE Trans on Power System，2000，15(4):1 232-1 239.

[11]YAMIN H Y，SHAHIDEHPOUR S M，LI Zuyi.Adaptive short-term electricity price forecasting using artificial neural networks in the restructured power markets[J].Electrical Power and Energy Systems，2004，26(8):571-581.