机会约束规划理论在有源配电网规划中的应用

董晓晶，李 荣，屈高强，党东升，康 健

(1.国网宁夏电力公司 经济技术研究院，宁夏 银川 750011;2.天津大学 电气与自动化工程学院，天津 300072)

随着我国节能减排战略的实施，新能源发电的分布式接入必将成为未来电网的发展趋势.而风、光等新能源发电的出力具有较大的随机波动特性，配电网规划也必将随之面临极大的不确定性，从而增加了配电网规划的难度.传统的有源配电网规划通常采取较为保守的规划原则，即在最恶劣的条件下校验分布式电源接入的可行性，[1]这将导致配电网规划中保留过多的备用容量，进而较大程度地降低规划方案的经济性.

为此，本文引入不确定规划理论，将不确定规划理论与有源配电网规划进行有机结合，通过分析规划中不确定性约束条件的置信度，在保证供电安全可靠性的前提下，实现经济效益的最大化.

1 不确定规划理论

1.1 不确定规划理论分类

不确定环境下的优化理论通常称为不确定规划，其提供了随机规划、模糊规划、粗糙规划，以及模糊随机规划建模与求解的统一原理.[2－5]不确定规划理论可以从以下3个角度进行分类:

(1)采用期望值构造数学模型，用不确定因素的期望值表达模型中不确定因素;

(2)采用机会约束规划构造数学模型，使不确定因素可以在较小可能性下不满足约束，即将硬性约束条件转变为柔性约束条件;

(3)采用相关机会规划构造数学模型，表达极大化规划目标实现的可能性.

不确定性规划理论基本框架如图1所示.

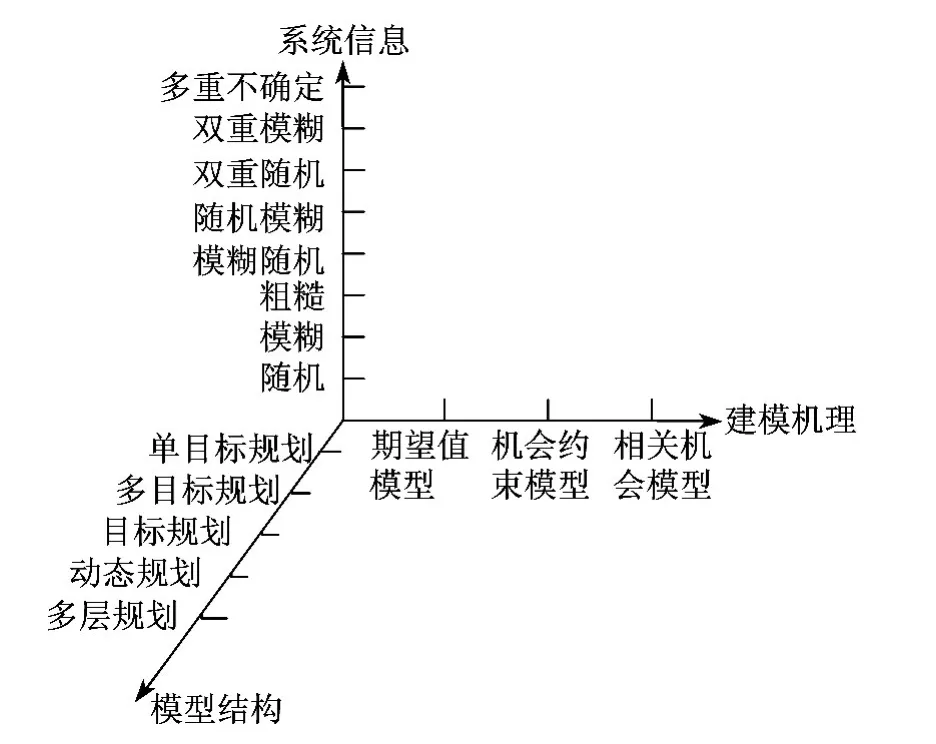
图1 不确定性规划理论基本框架

图1 是一个三维坐标系，概括了不确定规划的方法种类.坐标系中任何一个点均代表一种具体方法.如，点(粗糙，相关机会模型，多层规划)表示粗糙相关机会多层规划;平面“模型结构=动态规划”表示动态规划.

1.2 不确定规划模型

如图1中所示，基本的不确定变量包括随机变量、模糊变量和粗糙变量.包含不确定变量的函数统称为不确定函数.不确定规划中处理不确定函数的方法有以下几种:[5]

(1)以期望值表示不确定函数中的不确定因素;

(2)以概率性事件成立的置信度表示不确定因素;

(3)在不确定规划中极大化规划目标的概率实现最优规划，建立相关机会规划模型.

下面将详细介绍3种模型的机理.

1.2.1 期望值规划模型

在期望值规划模型中，取不确定变量的期望值使其满足约束条件，在此基础上进行优化，实现目标期望的最优.根据目标选取的不同，可以分为单目标模型、多目标模型等.期望值规划模型的数学表达式为:[5]

式中:E[·]——取期望值;

x——决策向量;

ξ——不确定变量;

f(x，ξ)——目标函数;

gj(x，ξ)——约束函数.

其中，E[gj(x，ξ)]≤0， j=1，2，3，…，p 是约束函数取得期望值的约束条件，maxE[f(x，ξ)]是目标函数期望的极大化.

若所解决的规划问题包含m个目标，则建立m个目标的规划模型:

式中:fi(x，ξ)——目标函数.

1.2.2 机会约束规划模型

机会约束规划模型要求不确定函数中的约束条件以一定的置信度成立，能够更准确地表示规划问题中的不确定因素.

假设x是决策变量，ξ是不确定变量，fi(x，ξ)是目标函数，gj(x，ξ)是约束函数，Pr{A}表示事件A成立的概率.由于不确定变量ξ的不确定性导致约束函数 gj(x，ξ)的不确定性，机会约束规划要求约束函数gj(x，ξ)所在的约束条件至少以一定的置信度成立，其数学表达式为:[5]

当且仅当gj(x，ξ)≤0成立的概率不小于α，即违反约束条件的风险小于(1－α)所求得的决策向量x才是有效的.

机会约束规划中约束条件更为一般的表达形式为:

1.2.3 相关机会规划模型

相关机会规划的核心是在不确定规划中极大化规划目标成立的概率.在前述的两种规划模型中，当规划问题被建模后，可行的解集本质上已经确定.然而在实际的规划中，所得到的最优规划结果可能无法施行.而相关机会规划可行的解集并不被限定.对于规划结果中给出的确定解，只要求其在实际规划中尽可能地施行.

以单目标相关机会规划、极大化目标函数为例，其数学模型为:

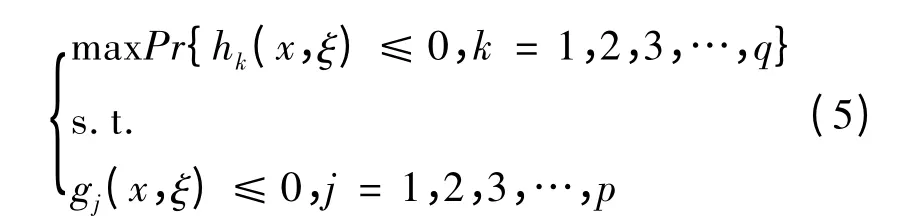
式中:x——n维决策变量;

ξ——不确定变量;

hk(x，ξ)≤0——规划的目标事件.

式(5)的机会约束规划模型可以表述为:在不确定变量所在的约束条件 gj(x，ξ)≤0，j=1，2，3，…，p 下极大化规划目标事件 hk(x，ξ)≤0，k=1，2，3，…，q 成立的概率.

多目标相关机会规划标准形式为:

其中，hik(x，ξ)≤0，k=1，2，3，…，qi为规划的目标事件.

2 有源配电网机会约束规划的数学建模

传统的有源配电网规划通常采用较为保守的策略:[1]在最恶劣的条件下校验分布式新能源接入的可行性.分布式新能源接入后，若电网仍能符合运行要求，则可以接入.因而采用传统方法规划后，系统中留有较多的备用容量，限制了规划方法的经济性.本文将不确定规划理论与有源配电网规划相结合，通过剖析二者之间的联系，结合典型分布式电源的出力模型对不确定变量类型、建模机理以及目标函数进行合理的选取，提出有源配电网的机会约束规划方法.

2.1 变量的选择

配电系统的不确定性主要包括随机性、模糊性、随机与模糊的双重不确定性.由于概率理论体系和模糊理论体系相互独立，将二者结合的双重不确定性问题较复杂，目前只能分开考虑.

在模糊理论体系下，确定模糊变量隶属度函数是关键，目前还没有一套成熟有效的方法来确定模糊变量的隶属度函数，多是根据实验或经验得到.现有的涉及风电出力与光伏出力的模糊规划问题一般选择采用梯形模糊函数来表示其出力不确定性.

相比于模糊规划，随机规划所采用的实际数据则更加全面具体，利用基于风速和光照强度的大量实际统计数据总结出分布规律，进而推导出风电出力和光伏出力的概率分布，结合具体区域特点，通过选择符合区域特征的参数可以更加准确地描述其出力的不确定性.因此，本文选择随机变量对有源配电网规划中不确定性进行描述.

2.2 分布式电源的出力模型

在随机体系下，由风力发电机出力与风速之间的关系式，并结合两参数Weibull分布的风速表达式，得到风力发电机的模型:[6]

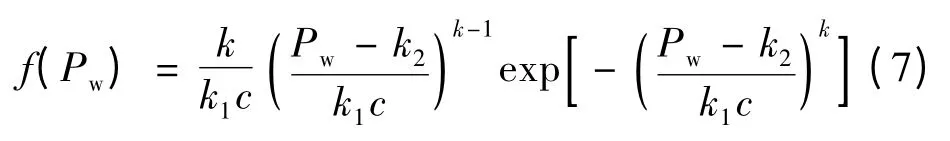
式中:k，k1——威布尔分布函数的形状因子;

c——威布尔分布函数尺度因子，可由不同场景中风速的均值和方差求得;

Pw——风力输电功率;

exp——自然指数函数.

大量的统计数据表明在白日里光照强度符合Beta分布，根据光照强度与光伏发电出力之间的关系可以得到光伏发电出力的概率密度函数为:

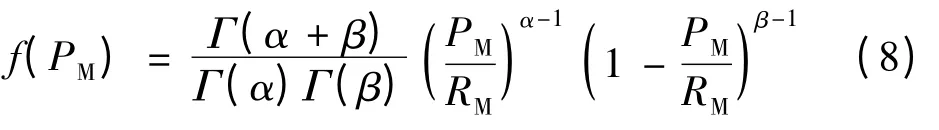
式中:RM——研究时间段内的最大光照强度;

α，β——Beta分布的形状参数，可由不同场景下的光照均值和方差求得;

Γ——伽玛函数;

PM——太阳能发电功率.

2.3 规划模型的选择

随机规划包括随机期望值模型、随机机会约束规划模型、随机相关机会规划模型.随机期望值模型的核心思想是将约束条件和目标函数中的不确定变量用期望值的形式表现出来.若在含分布新能源配电网规划中采用随机期望值规划模型，以节点电压约束和传输功率约束为例，其不确定性表达形式为:

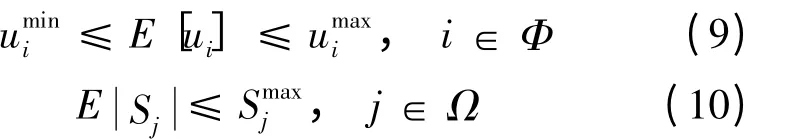
Φ——系统机电集合;

Sj——线路潮流;

Ω——线路集合.

随机机会约束规划的核心思想是使随机规划中的约束条件以一定的置信度成立.不同于期望值规划模型的目标函数期望值优化，随机机会约束规划的目标函数可以根据实际规划的需要进行选择并在约束条件至少以一定置信水平成立的基础上进行优化，具有更高的准确性，且可以根据规划的不同实际情况，对置信水平进行选择.其不确定性约束条件表达形式为:

(1)节点电压约束

式中:βu——电压约束的置信水平.

(2)支路传输功率约束

式中:βL——支路潮流约束的置信水平.

随机相关机会规划的主要思想是采用随机变量表示约束函数和目标函数，在约束条件下使规划目标成立的置信度极大化，从而给出最优规划结果.

分布式新能源出力的随机性、波动性导致配电网网络各节点电压，线路潮流等具有随机不确定性.而配电网规划的本质是基于包括节点电压约束、线路潮流约束等在内的安全约束、实现经济效益的最优.因此，综合分析3种随机规划模型的特性、配电网中分布式新能源出力的特性以及配电网规划的目标本质，采用以随机数据信息表达的机会约束规划方法，作为有源配电网的规划方法对配电网的科学规划更有利.

2.4 目标函数的选择

从目标函数角度划分，不确定规划可以分为单目标规划和多目标规划.在有源配电网规划中，目标函数可能包含多个不相容目标，作为单目标规划的推广，多目标规划定义为在一组约束条件下，优化多个不同的目标函数.[7]

针对有源配电网的规划特点，其目标函数通常选择实现总成本最小化，具体可表示为:

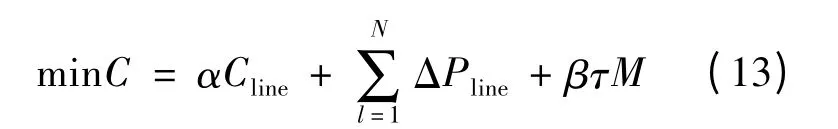
式中:Cline——线路投资费用;

α——年费用系数

ΔPline——供电线路有功损耗;

M——由线路可靠性转换得到的缺供电量;

β——区域产电比;

τ——负荷系数，反应负荷重要程度对经济效益的影响.

3 随机机会约束规划的应用实例

采用随机机会约束规划，对某城市部分配电网[8]进行分布式电源为边界条件的网络扩展规划.图2为该城市原有配电网络，其中实线为已有线路，虚线为待选线路，节点1，节点2，节点3为配电站节点，不在规划之列的其余节点均为负荷节点，其中节点33～57为新增负荷节点.

本算例实现了在分布式新能源位置与容量确定的情况下对配电网络进行扩展规划以达到经济效益最优.分布式电源指定的位置和容量如表1所示.

图3为在分布式新能源为边界条件的情况下得到的网络规划结果.结果显示网络布局使得绝大多数分布式电源位于辐射线路的中末端.该优化方案记为方案1.

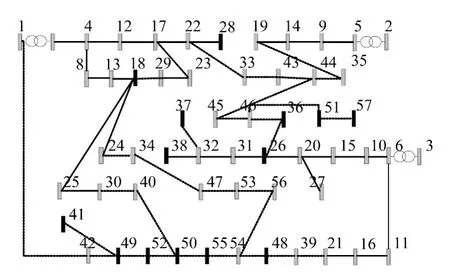
图2 某城市原有配电网络

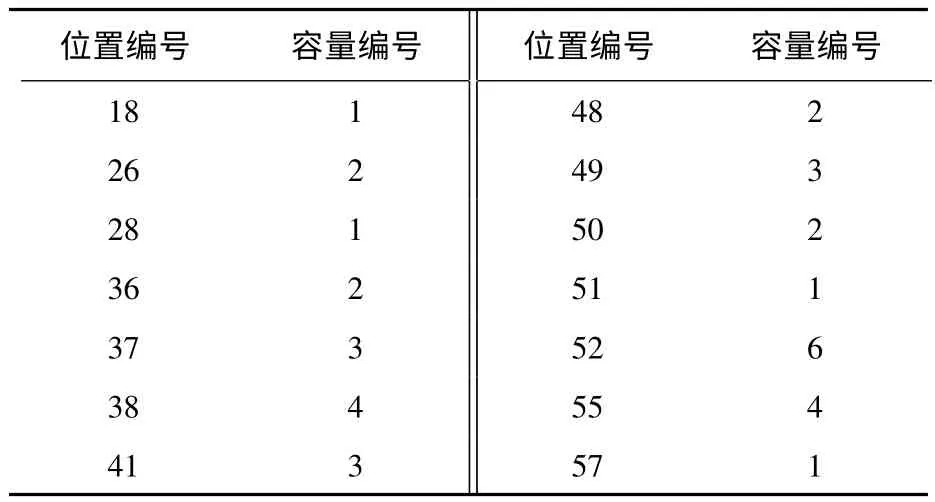
表1 规划后分布式电源位置和容量信息

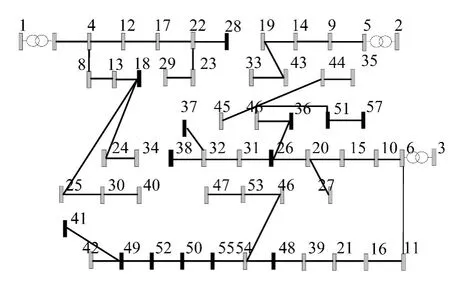
图3 网络优化结果

对于图1中的配电网络，如果不考虑置信水平，采用被动、保守接入DG的规划方法对于配电网进行扩展规划，所得优化结果记为方案2.方案1置信度为0.8，方案2置信度为1.方案1和方案2的成本费用对比如表2所示.

由表2可以看出，采用随机机会约束规划模型，使约束条件以一定的置信度满足条件，综合优化可以使线路总成本由1 701.251万元减少到1 554.789万元，减少了 8.61%，实现了成本的大幅度降低，经济效益得到了很大的提升.

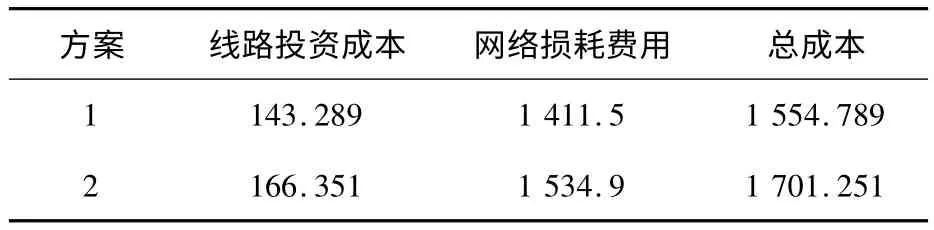
表2 方案1和方案2的线路成本对比万元/a

4 结语

结合风电与光伏的出力特点及各不确定规划方法特性，本文总结归纳出适应有源配电网规划的随机机会约束规划，并给出典型的目标函数和约束条件，采用随机机会约束规划方法对某城市已有配电网进行了扩展规划，结果验证了方法的可行性.

[1]欧阳武.含分布式发电的配电网规划研究[D].上海:上海交通大学，2009.

[2]彭锦，刘宝碇.不确定规划的研究现状及其发展前景[J].运筹与管理，2002，11(2):1-9.

[3]刘郁涵.不确定随机变量与不确定随机规划[D].北京:清华大学，2013.

[4]LIU B.Uncertain programming:a unifying optimization theory in various uncertain environments[J]. Applied Mathematics and Computation.2001，120(1-3):227-234.

[5]LIU Y，HA M.Expected value of function of uncertain variables[J]. Journal of Uncertain Systems，2010，4(3):181-186.

[6]周满.城市配电网规划的研究[D].杭州:浙江大学，2005.

[7]王成山，谢莹华，郑海峰，等.配电网扩展规划中分布式电源的选址和定容[J].电力系统自动化，2006，30(3):38-43.

[8]尹建兵.配电网规划研究[D].杭州:浙江大学，2011.