基于卡尔曼滤波算法的改进测频算法

许仪勋，李 旺，张敬周

(1.上海电力学院 电气工程学院，上海 200090;2.上海科学院 上科信息技术研究所，上海 201210)

频率是电力系统中一个非常重要的参数，也是衡量电能质量的重要指标之一.它涉及电力系统中发电、输电以及用电等各个环节，关系着居民生活中家用电器的正常工作寿命，影响着工业生产的产品质量，更影响着电表计量电量的准确性.因此，精准、快速地测量出动态电网中频率的实时数值，是保证电网安全运行的重要前提.目前，在工程中已经有许多频率测量方法，比如三点法、[1-2]过零点法、[3-4]傅里叶变换法、[5]经典卡尔曼滤波算法[6-8]以及各种相关的改进算法，都被广泛地应用于工程频率测量.然而这些算法各有优缺点:三点法原理简单，计算量小，但存在谐波和噪声干扰时测得的频率误差较大，限制了其在工程中的应用;过零点法也存在这一弊端，且对突变情况实时跟踪性差;傅里叶变换算法因为存在频谱泄露和栅栏效应，降低了频率计算的精度;经典卡尔曼滤波算法是高斯过程最优滤波的一种有效算法，但实时性差，当电网频率发生突变时，不能进行实时跟踪，甚至会出现发散情况.

针对过零点法和经典卡尔曼算法在测频时的缺点，当电网发生突变情况时，可采用拉格朗日线性插值算法和改进卡尔曼滤波算法，对突变点进行检测，对突变点处进行重新滤波，以此来解决突变时响应缓慢甚至是发散的问题.此外，还能够消除由闪变而产生短期突变的情况，达到稳定、可靠的测量目的，并且在滤波收敛速度上也有所提升.

1 过零点法

电压过零点法，又称为周期法，是基于电压信号观测模型 U(t)=Asin(2πft+φ)推导而来的，在电压信号波形一个周期内，通过测量相邻两个过零点间的时间间隔，从而可以推算出电网频率.该算法具有原理简单、计算量小、易于实现的特点，因而在实际工程中得到了广泛应用.

本文采用全周期过零点法，为了能够在短时间获取更多的过零点，分别采用对电压信号波形从正到负和从负到正过零点进行测量的方法.而在实际工程应用中，为了减小噪声污染的影响，可以利用线性插值算法来提高过零点法的计算精度，本文采用的是拉格朗日线性插值算法.[9]因此，通过计算相邻两个过零点之间的间隔数，再乘以时间间隔，就可以推算出相邻两个过零点的时间间隔，最后取其倒数便可推算出电网频率.

在实际电网中，电压波形会受到各种信号噪声的污染，使得电压信号波形为非标准正弦波.因此，在进行过零点计算时，还需对采样点数据进行预处理以及频率测量值的再处理，以提高频率计算的精度.

(1)不良过零点的剔除 为使程序更加严谨，提高频率测量的精度，防止电压波形在过零点处发生振荡现象，从而导致取错过零点.因此，除了要判断相邻两个采样点之积为非正外，还需验证计算得到的相邻两个采样点之间间隔的点数是否满足要求，若满足则保留，反之则应舍去.通过附加条件的限制，可以保证所取到的过零点是最符合要求的点.

(2)不良数据的剔除 在实际电网中，频率波动范围很小，然而当频率发生突变时，过零点法所测得的频率可能会出现一些误差很大的数据，远远偏离基波频率.针对这些不良数据，应对过零点法所测得频率值进行判断，符合要求的保留;反之则应剔除，并采用上一个测量值来代替此时的测量值，这样可以保证所测量的频率数据的可靠性与稳定性.

(3)减小测得的频率误差 在上述措施的约束下，过零点法所测得的频率数据与理论值相比，误差偏差仍较大，且按高斯白噪声序列围绕理论值上下波动.因此，为了减小数据误差范围，采用取均值的方法，能够有效地抑制随机性干扰，从而提高信噪比，达到减小数据误差范围的目的，使得处理后得到的频率围绕理论值的波动幅度减小，并为卡尔曼滤波提供高精度频率的观测序列.

2 卡尔曼滤波器

卡尔曼滤波算法[10-11]是以最小均方差为最佳估计原则，利用递归的方法解决离散系统线性滤波问题，其核心内容就是5个递推公式，主要描述了两个过程，即预测和修正.通过不断地“预测—修正”的递推方式进行计算，根据前一时刻估计值和最近时刻观察数据来估计信号的当前值，实现滤波的目的.假设线性离散系统的过程方程为:

输出方程为:

式中:X——系统的状态;

A，B——由系统的结构确定的矩阵;

Y——观测值;

C——观测矩阵;

W，V——系统噪声和观测噪声，随机变量且相互独立，一般假定W和V服从正态分布，且系统噪声和观测噪声的协方差阵分别为Q和R.

卡尔曼滤波算法就是要从观测值Y中得到状态X在最小均方差下的最佳逼近的估计值，其核心就是以下5个公式.

一是状态预测方程，即:

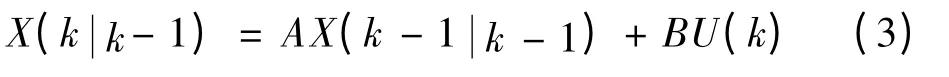
因为电压信号为单模型系统，所以它们只是一个标量，在该算法中，A值取为1;U(k)是 k时刻对系统的控制量，在该算法中没有控制量，因此U(k)为)是利用上一状态预测的结果)是上一状态最优的结果.

二是方差预测方程，即:

式(3)和式(4)就是对系统的预测.

三是状态估计方程，即:

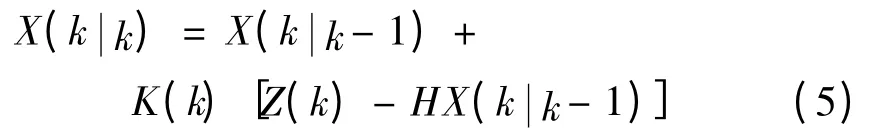
式中:K(k)——卡尔曼增益;

Z(k)——k时刻的测量值;

H——测量系统的参数.

四是滤波增益方程，即:

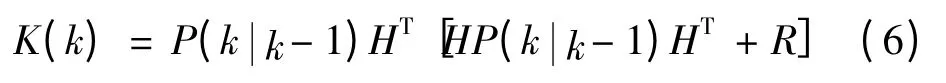
五是方差迭代方程，即:

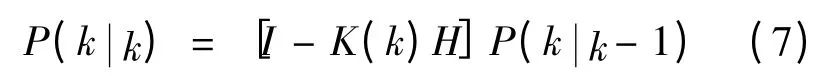
式中:I——单位矩阵，在该算法中，I取值为1.

式(5)至式(7)是对系统的修正，这样算法就可以自回归地运算下去.

在本文的算法中，将经数据处理后电压过零点法测得的频率数据作为卡尔曼滤波的观测值，然后根据卡尔曼滤波原理得到精度更高的频率估计值.然而卡尔曼滤波的增益K经过很长时间后会趋于一个较小的定值，即意味着卡尔曼滤波对以后的新数据不敏感，更依赖于以前的老数据.而假如此刻电网频率发生突变，由于此时卡尔曼滤波器对新数据不敏感，所以卡尔曼滤波器的响应速度缓慢，严重时甚至会出现滤波发散的现象，不能实时、准确地估计出电网频率.

为了解决这一难题，有研究者在20世纪90年代提出了著名的强跟踪滤波器，[12-13]使得滤波器在系统达到平稳状态时仍保持对缓变状态和突变状态的跟踪能力，但收敛速度较慢.而本文采用对突变点判别的方法，即通过判断均值法求得的频率序列之间的插值，当其绝对值大于预先设定的阈值时，则判定电网频率发生突变.此时，忽略突变后的5个周期内的过零点采样值，并用之前的估计值来替代，对以后的均值频率序列重新进行卡尔曼滤波.采用这一办法的缺点是舍弃了部分过零点，优点是也舍弃了在突变时所测得的偏差较大的频率值，提高了算法的收敛速度，比强跟踪滤波器的收敛周期更短，同时使得改进卡尔曼滤波器也具有较强的跟踪能力，能够实时、准确地估计出电网的频率.

3 算例仿真

为了验证该算法的可行性与正确性，本文通过Matlab软件进行实例仿真，并与经典卡尔曼滤波算法和强跟踪滤波算法对比模拟仿真，可清晰地观测出改进算法的优点.在实例仿真中，电压信号设为:

式(8)中的电压幅值取标幺值，基波频率f为50 Hz，每个采样周期有128个采样点，最后一项为高斯白噪声.

3.1 频率突变仿真

假设电网频率由基波频率突变为50.5 Hz，经过一段时间后，再由50.5 Hz突变为基波频率.此时改进卡尔曼滤波算法的频率估计值仿真图如图1所示，改进算法、经典卡尔曼算法和强跟踪算法频率估计值的对比分析如图2所示.

图1 改进卡尔曼算法仿真结果

由图1可知，在电网频率未发生突变时，改进算法所测得的频率精度很高;而当频率发生突变时，能快速响应，具有快速跟踪的功能，符合工程实际需求.

由图2可知，在电网频率稳定时，即前1/3部分可以看出这3种算法的仿真图形相同，它们的估计曲线完全重合，这也反映出这3种算法在稳定时的本质是一样的;而当电网频率发生突变时，经典卡尔曼滤波算法的响应速度缓慢，不能实时真实地反应出系统的频率，严重时甚至会出现发散的情况;而强跟踪滤波能够快速跟踪系统的实时频率，但收敛速度较慢;改进卡尔曼滤波算法不仅能快速跟踪突变后的频率，而且与强跟踪算法相比，收敛速度更快.

图2 频率发生突变时的对比仿真

3.2 频率和幅值同时发生突变仿真

假设当基波频率发生突变的同时，幅值也发生变化.频率由 50.5 Hz跳变到基波 50.0 Hz，然后又跳变到49.5 Hz;而幅值由1.0跳变到 0.85，最后又恢复到1.0.图3即为3个算法在频率和幅值发生突变时的仿真结果.

图3 频率和幅值发生突变时的仿真结果

由图3可知，无论在测量精度，还是在实时跟踪性和收敛速度上，改进卡尔曼算法都是最优的;而强跟踪滤波也能实时跟踪，但跟踪速度和收敛速度与改进算法相比较差;经典卡尔曼的响应速度依旧很缓慢，导致所估计出的频率值误差较大.

3.3 频率、幅值和相位同时发生突变仿真

假设频率由49.0 Hz跳变到49.5 Hz，经过一段时间后，再次跳变到50.0 Hz;而幅值由1.0跳变到0.85，再回恢复到 1.0;同时，初始相位由 30°突然变为45°，经过一段时间后又恢复到30°.图4即为3个算法在频率、幅值和相位同时发生突变时的仿真结果.

由图4可知，和前两个仿真结果一致，在频率测算的精度、突变的跟踪性和收敛性方面，改进后的卡尔曼滤波算法都是最优的.

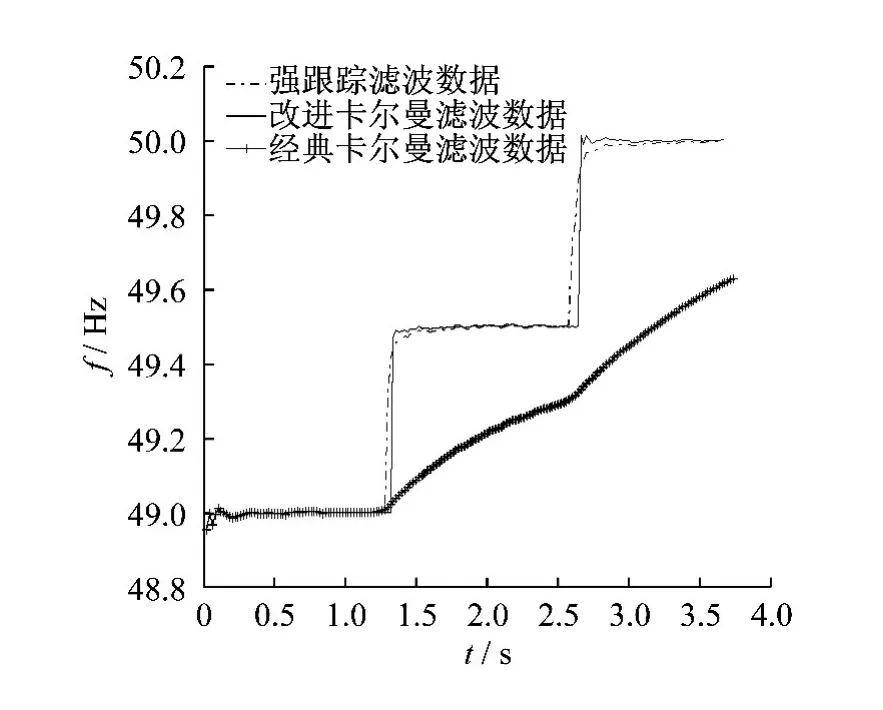
图4 频率、幅值和相位同时发生突变时的仿真结果

4 结论

(1)对数据采用滑窗均值处理方法，有效地抑制了随机性干扰，提高了信噪比，为卡尔曼滤波提供了较高精度的频率观测值;

(2)通过3个算例的仿真，并与其他算法进行比较可以看出，无论电网频率突变是先增大再减小，还是一直增大或减小，并伴随着电压幅值或相位的突变，改进卡尔曼滤波算法都能实时快速地响应，准确地估计出电网的频率值，充分证明了该算法的准确性和可行性.

(3)该算法实际应用于 ABN3000智能电能表上，在IAR编译环境下运用C语言进行编程，通过MSP430 47187芯片进行数据采集，也能精准地测量出实时频率值.

[1]洪慧娜，李晓明.电力系统基波交流采样频率修正的“三点”算法[J].高电压技术，2006，32(11):139-141.

[2]王东，王元利.一种电力系统频率的实时估算方法[J].继电器，2004，32(18):17-19.

[3]卞星明，文远芳，雷琴.电力系统测频算法比较[J].高电压技术，2006，32(5):111-114.

[4]宋红卫.基于线性插值的电网频率测量方法[J].工矿自动化，2012(6):99-102.

[5]张艳霞，陈旭林.基于DFT的电力系统频率及谐波精确算法[J].中国电力，2012，45(2):1-4.

[6]王志贤.最优状态估计与系统辨识[M].西安:西北工业大学出版社，2004:19-40.

[7]张勇刚，李宁，奔粤阳.最优状态估计:卡尔曼，H∞及非线性滤波[M].北京:国防工业出版社，2013:88-103.

[8]于静文，薛蕙，温渤婴.基于卡尔曼滤波的电能质量分析方法综述[J].电网技术，2010，34(2):97-103.

[9]杨永标，周捷.一种实用的高精度频率测量方法[J].继电器，2007(s1):272-275.

[10]张满生，张学庄.卡尔曼滤波器及其工程应用[J].计算技术与自动化，2008，27(1):136-139.

[11]钟暐.一种改进的卡尔曼滤波在 INS/GPS组合导航中的应用研究[D].长沙:中南大学，2009.

[12]赵仁德，马帅，李海舰，等.基于强跟踪滤波器的电力系统频率测量算法[J].电力系统保护与控制，2013，41(7):85-90.

[13]付梦印，邓志红，闫莉萍.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社，2010:100-108.