桥梁抖振力空间相关性对风-车-桥耦合动力响应的影响*

韩 艳，陈 浩，刘跃飞，蔡春声, 2，张建仁

(1. 长沙理工大学 桥梁工程安全控制省部共建教育部重点实验室，湖南 长沙 410114；2. 美国路易斯安那州立大学 土木与环境工程系，路易斯安那，巴吞鲁日 70803)

桥梁抖振力空间相关性对风-车-桥耦合动力响应的影响*

韩 艳1†，陈 浩1，刘跃飞1，蔡春声1, 2，张建仁1

(1. 长沙理工大学 桥梁工程安全控制省部共建教育部重点实验室，湖南 长沙 410114；2. 美国路易斯安那州立大学 土木与环境工程系，路易斯安那，巴吞鲁日 70803)

基于提出的抖振力模型和建立的风-车-桥耦合振动模型，发展了一种可以考虑抖振力空间相关性的风-车-桥耦合振动分析方法，并编制了相应的计算程序.以江顺长江大桥为工程背景，测试了桥梁抖振力的空间相关性和考虑车桥耦合作用的车桥气动参数，分析研究了桥梁抖振力空间相关性对侧风作用下桥梁和车辆耦合动力响应的影响.研究结果表明：桥梁抖振力空间相关性对桥梁动力响应有显著影响，对车辆的动力响应也有一定的影响.

大跨度斜拉桥；风工程；风-车-桥系统；耦合动力分析；抖振响应；相关性

风荷载作用下汽车-桥梁系统的振动、车辆行驶安全性和舒适性以及桥梁的疲劳损伤研究是桥梁工程的前沿课题之一.过去10年内，国内外学者在这方面进行了大量的研究并取得了大量的研究成果.夏禾[1], Xu和Guo[2], Cai和Chen[3]、李永乐[4]以及韩万水[5]等均建立了风-车-桥系统空间耦合振动分析框架，编制了相应程序，但目前风-车-桥系统空间耦合振动分析中均假设抖振力的空间相关性与来流脉动风速的空间相关性相同.这与实际情况不符，很多风-桥领域的研究已经证明这一点.

Larose[6]认为，假设抖振力的空间相关性等于来流风的空间相关性是导致预测抖振响应不确定性的一个主要原因，特别是对于类似闭口箱型桥面这类结构更是如此.Kimura等人[7]对扁平六角形和矩形断面进行了风洞试验，结果表明2种断面的抖振力中升力沿桥跨方向相关性要明显大于来流脉动风速的相关性.此外，许志豪[8]，韩艳[9]，赵传亮[10]，张冠华和赵林等[11]，李少鹏和李明水等[12]都对抖振力空间相关性进行了一定的研究，研究结果均表明：抖振力的空间相关性明显大于来流脉动风速的空间相关性.

本文提出了一套考虑桥梁抖振力空间相关性的风-车-桥耦合振动分析方法，并编制了相应的计算程序.以江顺长江大桥为工程背景，测试了桥梁抖振力的空间相关性，分析研究了桥梁抖振力空间相关性对侧风作用下桥梁和车辆耦合动力响应的影响.研究结果表明：桥梁抖振力空间相关性对桥梁动力响应有显著影响，对车辆的动力响应也有一定的影响.因此，在今后的风-车-桥系统耦合振动研究中有必要考虑桥梁抖振力的空间相关性.

1 考虑抖振力空间相关性的风-车-桥耦合振动分析理论

1.1 考虑抖振力空间相关性的抖振力模型

目前桥梁结构抖振响应分析往往忽略了实际抖振力与脉动风空间相关性的差异.本文基于一种新的抖振力模型来考虑抖振力的空间相关性.

作用于桥梁结构单位展长的抖振力表示为：

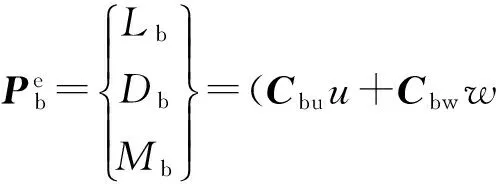
(1)

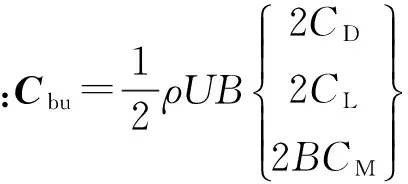
假设单元长度足够小，将抖振力平均分配到单元两端节点上，则节点力可表示为：

(2)

假设单元长度为L，整体坐标系下的抖振力功率谱密度函数SPbPb(ω)为

SPbPb(ω)=

.(3)

式中:抖振力的自功率谱密度函数SPbiPbi(ω)可以通过脉动分量u和w的功率谱密度函数得到，为

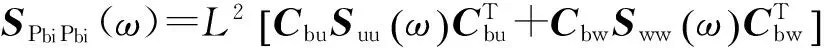
(4)

式中：Suu和Sww分别是u和w的功率谱密度函数.

而对于任意两点(i和j)抖振力的互功率谱密度函数，利用抖振力的空间相关性，可以表示为

SPbiPbj(ω)=

(5)

其中，

(6a)

(6b)

(6c)

(6d)

(6e)

(6f)

式中：CPR(P，R=D，L，M)是由风洞试验数据利用最小二乘曲线拟合得到的指数衰减系数.

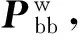
pi(x)m·Db(t)m+αi(x)m·Mb(t)m]．

(7)

式中：hi(x)m，pi(x)m和αi(x)m分别为第i阶振型在第m节点上的竖向、侧向和扭转角位移值；Lb(t)m，Db(t)m和Mb(t)m分别是第m节点上抖振力荷载.

1.2 风-车-桥耦合作用

采用拉格朗日法和虚功原理并引入模态叠加法建立风-车-桥耦合振动分析模型，具体的相关理论介绍详见文献[13]，只需将本文模拟的考虑抖振力空间相关性的桥梁广义抖振力向量代替完全相关于脉动风场的桥梁广义抖振力向量，则风-车-桥耦合运动方程为

(8)

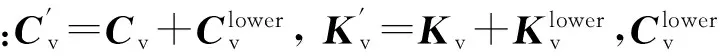
本文采用ANSYS软件建立桥梁有限元模型，计算桥梁的动力特性，获得桥梁结构的振动模态、固有频率以及模态质量等参数，根据上面的理论基于MATLAB软件编制了相应的风-车-桥耦合振动分析程序.

2 算例分析

2.1 计算参数

本文以江顺大桥为工程背景，江顺大桥是一座主跨700 m的钢-混凝土混合斜拉桥，其跨径布置为：60 m (混凝土) +176 m + 700 m +176 m + 60 m (混凝土)，主桥全长1 172 m，总体布置图如图1所示.表1给出了江顺大桥考虑车辆影响的桥梁断面三分力系数(取自文献[14])，图2给出了考虑车辆影响的江顺大桥气动导数(取自文献[15]).桥梁抖振力的空间相关性可以用相关函数表示，相关函数通常表示成指数衰减函数

(9)

式中：C为衰减因子，即抖振力的空间相关系数，如式(6a～f)；f为抖振力的频率；Δ为两排测压孔之间的距离；U为平均风速.在主梁节段模型的不同断面上布置了测压孔，通过对各个截面进行压力积分得到各截面的抖振力，然后对抖振力进行相关分析并采用非线性最小二乘拟合得到抖振力的空间相关系数，见表1.文中对脉动风场的相关性没有进行相关测试，根据经验取顺风向和竖风向脉动风空间相关系数均为16.

采用ANSYS建立桥梁有限元模型，计算得到的桥梁结构前10阶动力特性见表2，结构阻尼比取0.005.首先分别取前10和20阶桥梁振型进行车桥耦合振动计算，计算得到的桥梁和车辆动力响应非常接近，故为了节省计算时间，桥梁振型只取前10阶进行相关计算.

本文采用侧面面积比较大的集装箱2轴车辆作为分析对象，车辆的模型及主要参数参考文献[13]，车辆的气动力系数参考文献[14]，如图3所示.

(a) 立面图 (b) 标准钢箱梁断面图

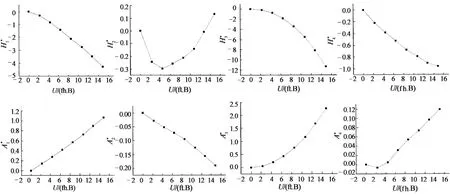
图2 江顺大桥0度攻角考虑繁忙车流影响的气动导数

表1 江顺大桥主要气动参数Tab.1 Main parameters for Jiangshun Bridge

表2 江顺大桥的前10阶动力特性
Tab.2 Dynamic properties of the first 10 modes for Jiangshun Bridge

阶数固有频率/Hz模态质量/kg模态振型阶数固有频率/Hz模态质量/kg模态振型10.087651598174.2主梁纵飘60.37517317623.5主梁一阶反对称竖弯20.20887929131.0主梁一阶对称侧弯70.51057924290.6主梁二阶对称竖弯30.28945550585.1主梁一阶对称竖弯80.601310126095.3主梁一阶反对称侧弯40.295817876645.1塔的反对称侧弯90.635210660412.5主梁二阶反对称竖弯50.296117958582.4塔的对称侧弯100.67453433791.4主梁一阶对称扭转

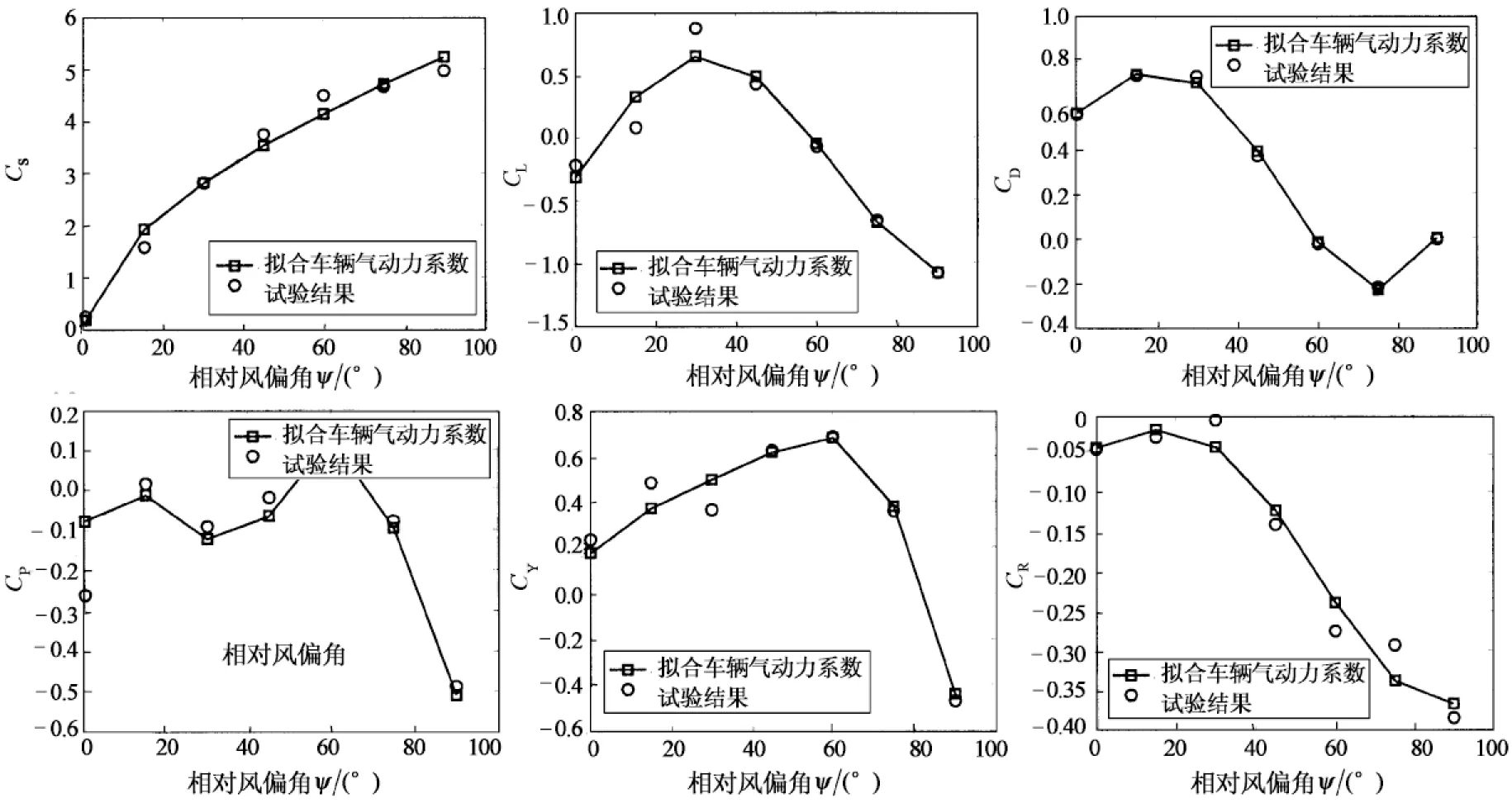
图3 车辆气动力系数Fig.3 The aerodynamic force coefficients of the vehicle vs. yaw angle ψ

顺风向的功率谱采用Kaimal谱，竖风向采用Lumley和Panofsky提出的功率谱[16]，采用Davenport相关函数，顺风向和竖风向脉动风速的空间相关系数均取16.频率采样点数为1 024，截止频率为2π，平均风速为20 m/s.采用谐波合成法[17]沿桥纵向共模拟了99个点的脉动风时程.假定桥面粗糙度是一零均值的平稳高斯随机过程，利用离散傅立叶逆变换计算得到路面不平度值，本文只考虑良好路面一种情况，粗糙度系数取20× 10-6m3/circle.

2.2 计算结果及分析

2.2.1 抖振力空间相关性对桥梁动力响应的影响

计算中桥梁气动参数取表1和图2给出的气动参数，车辆气动参数取图3中拟合的车辆气动力系数，平均风速取5 m/s, 10 m/s, 15 m/s, 20 m/s, 25 m/s和30 m/s，车辆行驶速度为20 m/s，考虑一辆车辆，车辆距桥中心线的距离为15 m.受篇幅限制，本文只给出部分计算结果，图4给出了平均风速为20 m/s时桥梁位

图4 抖振力空间相关性对桥梁位移响应的影响

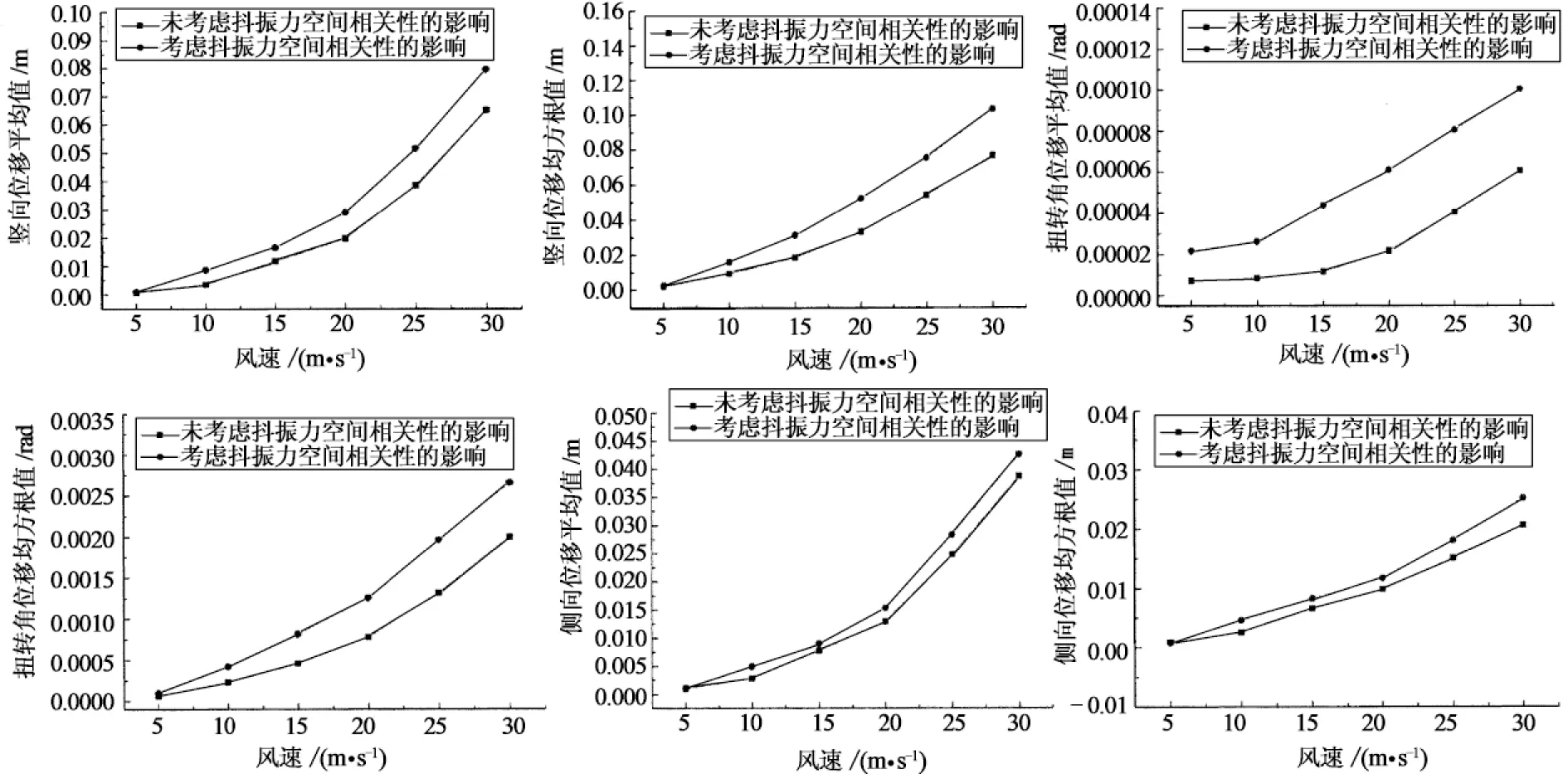
图5 桥梁位移响应随风速变化情况

移响应沿桥纵向位移的变化情况.图5给出了桥梁跨中位移响应随风速变化的情况.

由图4可见，抖振力空间相关性对桥梁的动力响应影响显著，考虑抖振力空间相关性的桥梁动力响应明显大于未考虑抖振力空间相关性的结果.抖振力空间相关对跨中位移的影响大于对边跨位移的影响，对侧向位移的影响小于竖向及扭转角位移的影响.

由图5同样可以看出考虑抖振力空间相关性的桥梁动力响应明显大于未考虑抖振力空间相关的，而且影响随着风速增大而增大.

2.2.2 抖振力空间相关性对车辆动力响应的影响

图6给出了车辆相对位移响应随着风速变化的情况.作用在车辆上的相对风速的风偏角随着风速的增大而增大.从图中可以看出，车辆竖向位移的平均值随着风速的增大而先增大后减小，车辆侧翻角位移平均值随着风速的增大而减小，车辆侧向位移平均值随着风速的增大而减小，车辆各方向位移平均值的变化趋势与对应的车辆气动力随着相对风偏角的变化趋势一致.而且基本不受抖振力空间相关性的影响.车辆各方向位移的均方根均随着风速的增大而增大，抖振力空间相关性对其有一定的影响.在低风速时，基本没有影响，在高风速时，使车辆相对竖向位移的均方根减小，而使车辆相对扭转角和侧向位移的均方根略微增大.

图6 车辆相对位移响应随风速变化情况

3 结 论

本文提出了一套考虑桥梁抖振力空间相关性的风-车-桥耦合振动分析方法，并编制了相应的计算程序.通过对江顺大桥的计算分析，可以得出以下结论：

1) 考虑抖振力空间相关性的桥梁动力响应明显大于未考虑抖振力空间相关性的结果，而且这种影响随着风速增大而增大.另外，抖振力空间相关对跨中位移的影响大于对边跨位移的影响，对侧向位移的影响小于竖向及扭转角位移的影响.

2) 抖振力空间相关性对车辆各相对位移响应的平均值基本没有影响，但对车辆各相对位移响应的均方根有一定影响，在高风速时，使车辆相对竖向位移的均方根减小，而使车辆相对扭转角和侧向位移的均方根略微增大.

因此，在风-车-桥耦合振动分析中有必要考虑抖振力空间相关性的影响.

[1] 夏禾, 徐幼麟, 阎全胜. 大跨度悬索桥在风与列车荷载同时作用下的动力响应分析 [J]. 铁道学报, 2002, 24(4):83-91.

XIA He, XU You-lin, YAN Quan-sheng. Dynamic response of longspan suspension bridge to high wind and running train [J]. Journal of the China Railway Society, 2002, 24(4): 83-91. (In Chinese)

[2] XU Y L， GUO W H. Dynamic analysis of coupled road vehicle and cable-stayed bridge system under turbulent wind [J]. Engineering Structures, 2003, 25(4):473-486.

[3] CAI C S, CHEN S R. Framework of vehicle-bridge-wind dynamic analysis[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(7/8):579-607.

[4] LI Y L, QIANG S Z, LIAO H L,etal.Dynamics of wind-rail vehicle-bridge systems [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(6):483-507.

[5] 韩万水, 陈艾荣. 风-汽车-桥梁系统空间耦合振动研究 [J]. 土木工程学报, 2007, 40(9):53-58.

HAN Wan-shui, CHEN Ai-rong. Three-dimensional coupling vibration of wind-vehicle-bridge system [J]. China Civil Engineering Journal, 2007, 40(9): 53-58.(In Chinese)

[6] LAROSE G L.The dynamic action of gusty winds on long-span bridges[D]. Copenhagen: Department of Civil Engineering, Technical University of Denmark, 1997:105-180.

[7] KIMURA K,FUJINO Y,NAKATO S.Characteristics of buffeting forces on flat cylinders [J]. Journal of Wind Engineering and Industrial Aerodynamics，1997, 69/71:365-374.

[8] 许志豪. 紊流风对大跨度分体双箱梁桥梁的作用 [D]. 上海: 同济大学土木工程学院, 2006: 151-180.

HUI M C H .Turbulent wind action on long span bridges with separated twin-girder decks [D]. Shanghai: School of Civil Engineering, Tongji University, 2006:151-180. (In Chinese)

[9] 韩艳. 桥梁结构复气动导纳函数与抖振精细化研究 [D]. 长沙: 湖南大学土木工程学院, 2007: 155-165.

HAN Yan. Study on complex aerodynamic admittance functions and refined analysis of buffeting response of bridges [D]. Changsha: College of Civil Engineering, Hunan University, 2007:155-165. (In Chinese)

[10] 赵传亮. 箱形主梁抖振力空间相关性及其对桥梁抖振响应的影响 [D]. 上海: 同济大学土木工程学院, 2009: 69-87．

ZHAO Chuan-liang. Box girder buffeting influence of spatial correlation and buffeting response of the bridge [D]. Shanghai: School of Civil Engineering, Tongji University, 2009:69-87. (In Chinese)

[11] 张冠华，赵林，葛耀君. 流线型闭口箱梁断面风荷载空间相关性试验研究 [J]. 振动与冲击, 2012, 31(2):76-80.

ZHANG Guan-hua, ZHAO Lin, GE Yao-jun. Spatial correlation of wind loads for cross-section of a streamlined closed box girder [J]. Journal of Vibration and Shock, 2012, 31(2):76-80. (In Chinese)

[12] 李少鹏，李明水，马存明，等. 大跨桥梁抖振力与脉动风速空间相关性的对比研究 [J]. 空气动力学学报, 2013, 31(6):797-800.

LI Shao-peng, LI Ming-shui, MA Cun-ming,etal.Comparison of the spatial correlation of the buffeting force on long span bridge and wind fluctuations [J]. Acta Aerodynamica Sinica, 2013, 31(6): 797-800. (In Chinese)

[13] HAN Y, CAI C S, ZHANG J R,etal.Effects of aerodynamic parameters on the dynamic response of road vehicles and bridges under cross winds [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 134:78-95.

[14] HAN Y, HU J X, CAI C S,etal.Experimental and numerical study of aerodynamic forces on vehicles and bridges [J]. Wind and Structures, 2013, 17(2):163-184.

[15] HAN Y, LIU S Q, CAI C S,etal.Experimental study on aerodynamic derivatives of a bridge cross-section under different traffic flows [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 133:250-262.

[16] LUMLEY J L, PANOFSKY H A. The structure of atmospheric turbulence [M]. New York: Wiley, 1964: 50-210.

[17] DEODATIS G. Simulation of ergodic multivariate stochastic processes [J]. Journal of Engineering Mechanics, ASCE, 1996, 122(8): 778-787.

Effect of the Coherence of Buffeting Forces of Bridges on theCoupled Dynamic Responses of Wind-vehicle-bridge System

HAN Yan1†,CHEN Hao1,LIU Yue-fei1,CAI Chun-sheng1, 2,ZHANG Jian-ren1

(1. Key Laboratory for Safety Control of Bridge Engineering,Ministry of Education and Hunan Province, Changsha Univ of Science & Technology, Changsha, Hunan 410114, China;2. Dept of Civil and Environmental Engineering, Louisiana State Univ, Baton Rouge, LA 70803, USA)

Based on the buffeting force model and the model for the wind-vehicle-bridge system presented in the paper, an approach to study the coupling vibration of wind-vehicle-bridge system considering the coherence of buffeting forces was developed and the corresponding calculating program was built. The application of the proposed methodology on the Jiangshun Bridge in China was presented as a numerical example. The coherence of the buffeting forces of the bridge and the aerodynamic parameters of the bridge and the vehicle considering the aerodynamic interference between the bridge and the vehicle were measured in wind tunnel. The effect of the coherence of buffeting forces of the bridge on the dynamic performance of both the bridge and the vehicles under cross winds were discussed. It is found that the coherence of the buffeting forces of the bridge has significant effect on the dynamic responses of the bridge, and some impact on the dynamic responses of the vehicle.

long-span cable-stayed bridge;wind engineering; wind-vehicle-bridge system; coupled dynamic analysis;buffeting effects; coherence

1674-2974(2015)09-0082-07

2014-11-06

国家重点基础研究计划(973计划)资助项目(2015CB057706)；国家自然科学基金资助项目(51178066，51208067，51278069), National Natural Science Foundation of China(51178066, 51208067, 51278069)；长沙理工大学桥梁工程安全控制省部共建教育部重点实验室开放基金资助项目(12KB01)；交通部西部交通科技项目重大科技专项资助项目(2011318824140)

韩 艳 (1979—)，女，江苏连云港人，长沙理工大学副教授，博士

†通讯联系人，E-mail: ce_hanyan@163.com

U441.3

A