二氧化碳管道输送过程管径设计分析*
高瑞民,赵晓兰,陈光莹,梁志武,那艳清
(湖南大学 化学化工学院 化石能源低碳化高效利用湖南省重点实验室,湖南 长沙 410082)
二氧化碳管道输送过程管径设计分析*
高瑞民,赵晓兰,陈光莹,梁志武†,那艳清
(湖南大学 化学化工学院 化石能源低碳化高效利用湖南省重点实验室,湖南 长沙 410082)
根据影响管径设计的因素,从质量流量、管长和压降3个方面对Rubin管道设计模型进行分析,根据分析结果建立相应的数值模型;使用MIT管道设计模型验证所建数值模型的可靠性;在此基础上从管道总资本成本和中间加压站成本两方面分析管道经济成本.研究结果表明,模型各变量的变化规律及相应数值模型类型均与验证模型相同,且有很好的相关性(其决定系数R2均大于0.970).
数值模型;管道设计;二氧化碳;成本分析
CO2管道运输自20世纪70年代出现以来,一直被广泛用于提高原油采收率(EOR)项目中CO2的运输[1].据不完全统计,世界上在运行的和规划中的EOR项目CO2输送管道约有2 600 km[1].管道运输过程中CO2多以密相流或超临界流状态被输送,但输送方式(一般流体、密相和超临界输送)、输送管道和设备要根据CO2气源的实际情况以及不同输送方式的特点等因素来选择.管道运输费用受多方面因素的影响,如人文、社会、地质条件、管道材料费用等,管道材料费用又受到管道长度、直径、材质以及中间加压站的影响[2].准确分析这几个因素对管道的影响,对于CO2管道运输成本的估算具有重要的意义.
管道直径计算是CO2管道运输成本估算中最重要的参数之一,许多研究者对管径这一关键参数进行了研究[3-5].2003年Zhang等人[6]从系统优化、能耗、综合经济成本这三个方面分析管道运输并比较超临界流体输送、过冷液体输送这两种输送方式,发现在绝热和等温条件下过冷液体输送可以实现能量的有效利用,减少二氧化碳运输的成本.2006年麻省理工学院的实验室针对能源和环境问题,发表了一项关于二氧化碳存储的经济学研究,提出了迭代法计算管径的MIT模型[7];2008年Mccoy等人[4]用Rubin模型作为管道性能模型,评估了运输的总成本以及二氧化碳的单位成本,并且分析了美国不同地区管道运输的成本,所建的经济成本模型可以估计潜在的二氧化碳捕获与封存(CCS)的成本;2008年Mccoy等人[8]研究了盐碱含水层和油藏中的CO2管道运输和存储成本,从封存和驱油两方面分析了管道运输的成本.
现有的管径计算模型很难直观反映影响管径的主要因素(质量流量、管长和压降)与管径间的内在联系.因此,本文以Rubin模型为例,利用计算机编程研究模型各因素对管径的影响,并用统计学软件SPSS分析管径随各因素的变化规律,建立相应的数值模型;在同等条件下与MIT模型对比,验证所建立数值模型的准确性;在此基础上进行管道经济成本估算,从管道设计和成本分析两个层面上对CO2管道运输进行综合分析.
1 Rubin模型描述
Rubin模型的计算依据是管道运输过程中CO2的能量守衡,该模型的建立基于3个假设:1)管道进出口的压力为常数;2)杂质在整个管道中均匀分布;3)忽略管道内CO2的压缩性.模型描述如下[4]:
(1)
(2)
(3)
(4)
(5)
式中:h1,h2分别为管道起始、终点的海拔,m;P1,P2为管道进出口压力,MPa;Pave为管道的平均压力,MPa;Zave为管道平均压缩因数;f为管道摩擦系数;ε为管道粗糙度 ,一般取0.045 7 mm;D为管道内径,m;T为温度,K;L为管道长度,km.
Rubin模型对最优管径的求解是一个复杂的迭代过程,求解时,首先需要假定一个管道直径的初始值,计算出流体的雷诺数、摩擦阻力等参数,据此求出一个新的管径值,用该值与初值进行比较,如果差值在可接受的范围内,则认为该值为管道直径[4].如果差值不满足条件,则重复上述过程,直到满足要求为止.具体流程如图1所示.
2 Rubin模型各影响因素与最优管径之间数值模型的建立及验证分析
本文使用Peters MS等人的最优管径模型[9]估计管道直径的初始值,利用软件编程,迭代计算管道直径.在给定的参数条件下(表1),得到了质量流量和管长对管径的影响以及质量流量对压降的影响.
表1 管道设计参数
Tab.1 Pipeline design parameters
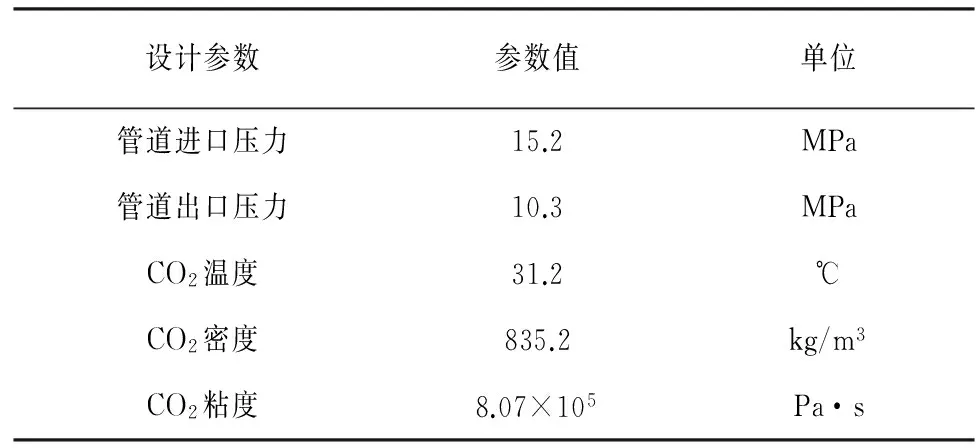
设计参数参数值单位管道进口压力15.2MPa管道出口压力10.3MPaCO2温度31.2℃CO2密度835.2kg/m3CO2粘度8.07×105Pa·s
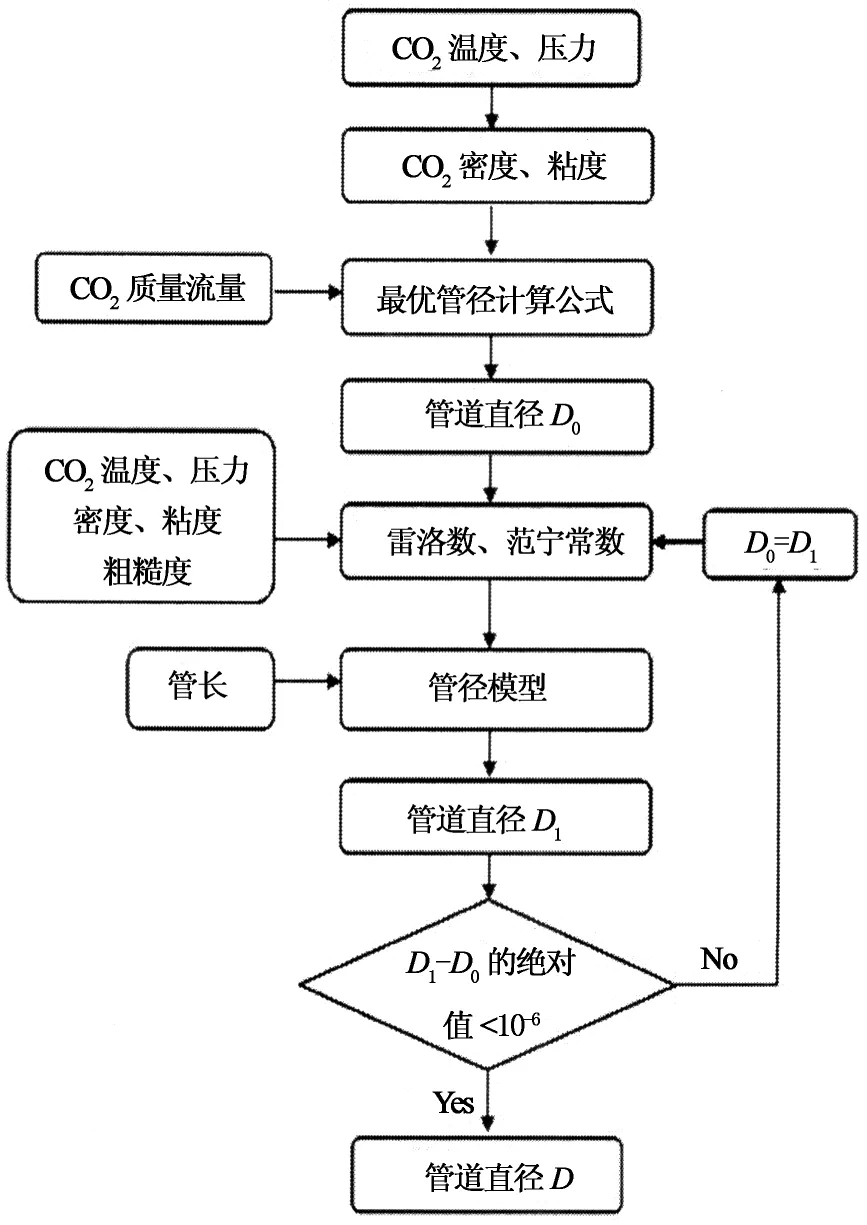
图1 管径计算过程
2.1 质量流量对管径的影响
图2为质量流量与管径的关系图,由图可知:管径随质量流量的增加而增加.由于流体在管道内输送时存在流动阻力,随着质量流量的增加湍流阻力增大,而管径的增加有助于减小流体输送的阻力.因而随着质量流量的增加,最优管径也随之变大.
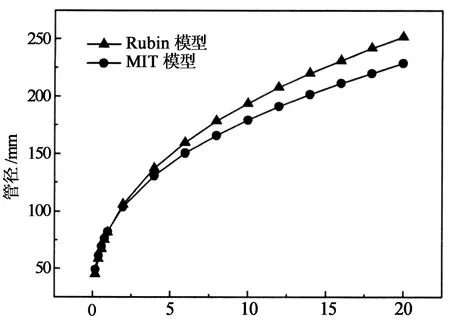
CO2质量流量/(kt·d-1)
2.2 管长对管径的影响
图3是管长与管径的关系图,由图可知:管径随管长的增加而增加.这是因为随着管长的增加,输送过程的压降增加;为了平衡过程的压降,需增大管径,使得管道内流动的CO2的流速减小,从而减小输送过程的压降.
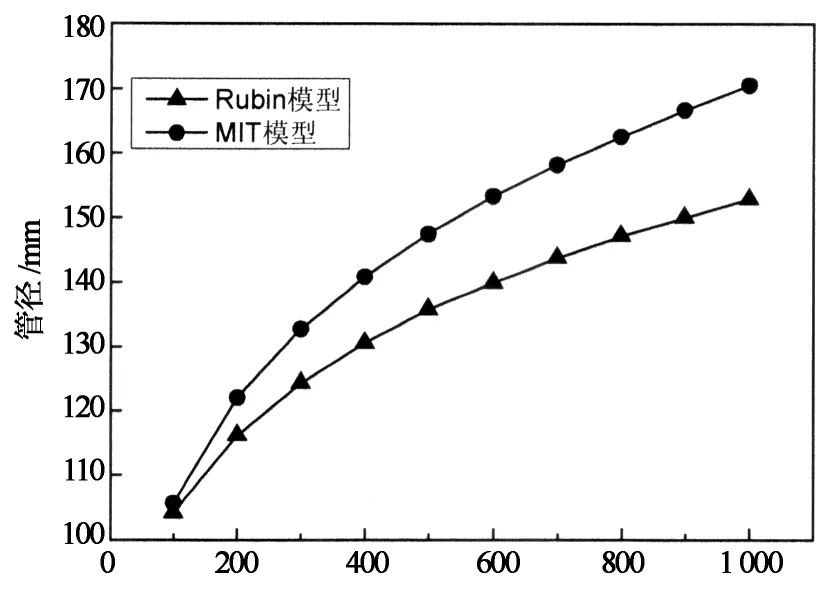
管长/km
2.3 压降与质量流量的关系
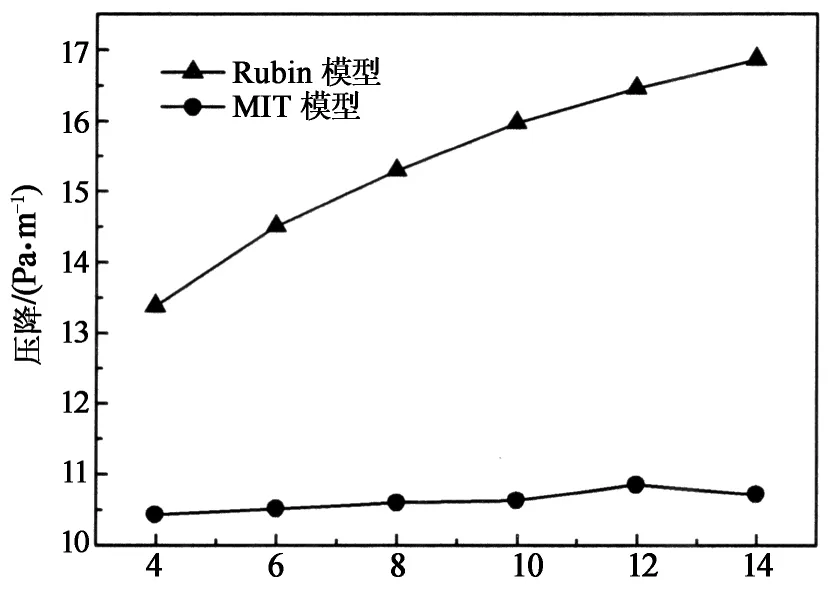
根据达西-韦史巴赫方程[1],压降取决于管道的直径、内部粗糙度以及被运输流体的密度、流速和粘滞度.运用软件Aspen plus 模拟CO2液化运输过程,得到压降与质量流量之间的关系(图4).由图4可知:随着质量流量的增加,管道压降逐渐增加.这是因为随着质量流量的增加,过程的摩擦阻力增大.
CO2质量流量/(kt·d-1)
用统计学软件SPSS对Rubin模型各影响因素与最优管径之间的图像作多元线性回归,得到数据模型(表2).从表中可以看出,所建数据模型具有显著的统计学意义,可以很好地说明各变量之间的关系.
表2 各变量间的数据模型
Tab.2 The numerical models for each variable
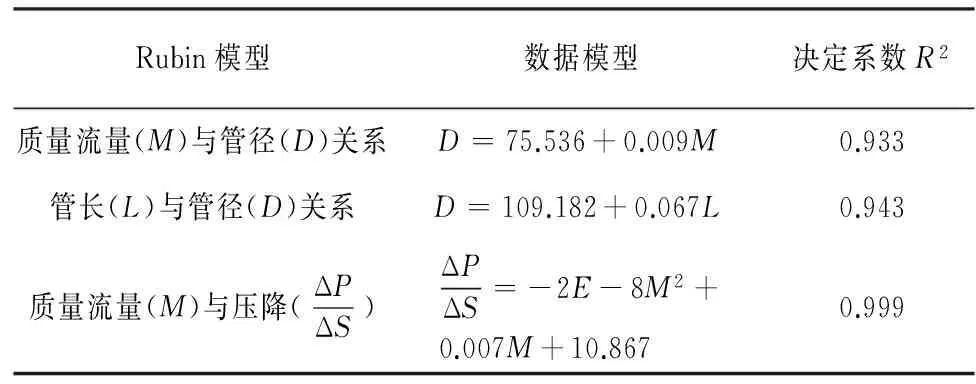
Rubin模型数据模型决定系数R2质量流量(M)与管径(D)关系D=75.536+0.009M0.933管长(L)与管径(D)关系D=109.182+0.067L0.943质量流量(M)与压降(ΔPΔS)ΔPΔS=-2E-8M2+0.007M+10.8670.999
为进一步验证所建数值模型的准确性,本文使用MIT管道模型[7]作为参照,通过计算得到各影响因素与管径间的关系,检验所建立模型的精度和适用性.MIT 模型的设计原理和Rubin模型类似,都基于能量守恒定律.MIT 模型成本分析的数据来源为天然气管道施工历史成本,选用MIT 模型作为对比分析,有利于建立新的成本分析数据.通过模型验证(如图2~图4所示),MIT模型与Rubin模型的结果非常接近,很好地验证了Rubin模型所建立的数据模型的准确性和可信度.
3 各变量与管道总资本间的数值关系分析
管径计算模型为管道建造施工及成本估算提供了重要的参数,管道运输的商业化使得人们更多地关注其经济效益.因此,本文从质量流量、管长对管道总资本成本的影响以及中间加压站(弥补压降)对能耗的影响这几个方面对管道总资本成本做相应的经济分析.
3.1 质量流量对管道总资本成本的影响
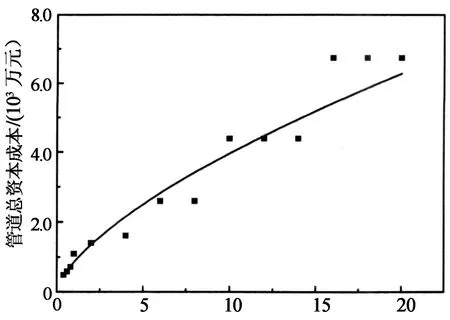
图5是质量流量与管道总资本成本的关系图,由图可知:在管长一定的情况下,模型的管道总资本成本随着质量流量的增加而增加;由于管道内径的对称化,所以在某一段质量区间范围内,管道总资本成本相同;用统计学软件SPSS对图像数据做曲线拟合估计,得到回归方程y=86 558(X0.665),决定系数R2为0.971,可见管道的总资本成本和质量流量呈幂指数关系.
3.2 管长对管道总资本成本的影响
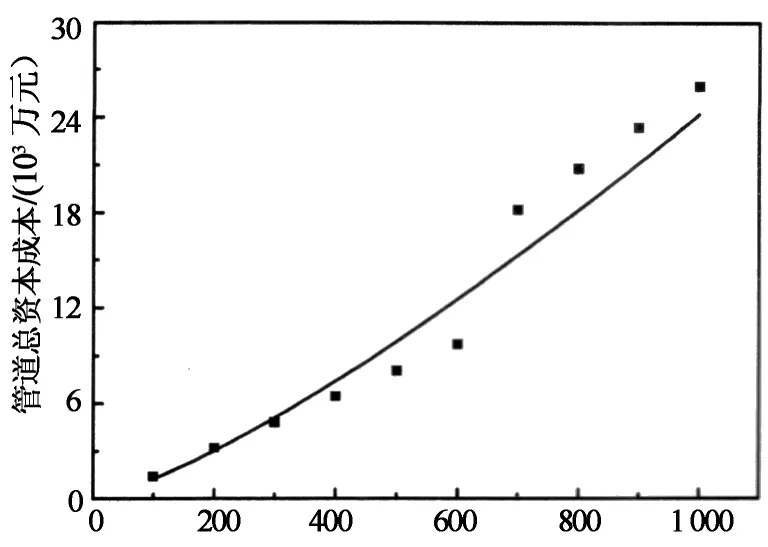
图6是管长与管道总资本成本的关系图,由图可知:在质量流量一定的情况下,随着管长的增加,管长对管道总资本成本的影响逐渐增大;用统计学软件SPSS对图像数据做曲线拟合估计,建立的回归方程为y=33 216(X1.287),决定系数R2为0.974,可见管道的总资本成本和管长呈幂指数大于1的幂指数关系.
质量流量/(kt·d-1)
管长/km
3.3 中间加压站对能耗的影响
长距离管道运输过程中管道的运输压力小于10.3 MPa时需要通过压缩机在过程中增压(中间加压站).流体在管道中的压力会随着运输管道流体流量和管径的变化而变化[2].
用Aspen plus模拟得到的CO2运输过程中压缩机加压时的能耗情况.随着CO2流体质量流量的增加其能耗相应增加,压缩机的能耗和CO2的质量流量呈线性关系 (y= 0.099 7X),决定系数R2=1.000,可见模型具有很好的拟合能力,可以用于加压站的成本估计.
4 结 论
管径设计是管道输送系统设计过程中的关键步骤,通过对影响管道设计的因素分析以及管道的成本分析得到以下几点结论:
1)管径随质量流量和管长的增加而增加,管道压降随着质量流量的增加逐渐增加;
2)用统计学软件SPSS对图像数据进行分析处理,分别建立了管长和质量流量与管径、质量流量与压降的数值模型;
3)将管径-管道材料成本之间的关系,转换为CO2质量流量-管道总资本成本,减少了计算管径这一过程.
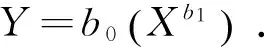
[1] 拉克利. 碳捕获与封存[M]. 北京:机械工业出版社, 2011: 283-284.
RACKLEY S A. Carbon capture and storage[M]. Beijing: China Machine Press, 2011:283-284. (In Chinese)
[2] 高蓝宇. 二氧化碳吸附和输送技术研究[D]. 杭州: 浙江大学能源工程学院, 2011.
GAO Lan-yu. Research on CO2adsorption and transportation technology [D]. Hangzhou:College of Energy Engineering, Zhejiang University, 2011. (In Chinese)
[3] BOCK B, RHUDY R, HERZOG H,etal. Economic evaluation of CO2storage and sink enhancement options[EB/OL]. Other information: PBD: 1 Feb 2003. http://brbock. com/RefFiles/40937R04. pdf.
[4] MCCOY S T, RUBIN E S. An engineering-economic model of pipeline transport of CO2with application to carbon capture and storage [J]. International Journal of Greenhouse Gas Control, 2008, 2(2): 219-229.
[5] VANDEGINSTE V, PIESSENS K. Pipeline design for a least-cost router application for CO2transport in the CO2sequestration cycle [J]. International Journal of Greenhouse Gas Control, 2008, 2(4): 571-581.
[6] ZHANG Z X, WANG G X, MASSAROTTO P,etal. Optimization of pipeline transport for CO2sequestration [J]. Energy Conversion and Management, 2006, 47(6): 702-715.
[7] MCCOLLUM D L, OGDEN J M. Techno-economic models for carbon dioxide compression, transport, and storage & correlations for estimating carbon dioxide density and viscosity[D]. Davis, CA:Institute of Transportation Studies Working Paper, SectionⅢ, 2006.
[8] MCCOY S T. The economics of CO2transport by pipeline and storage in saline aquifers and oil reservoirs. engineering & public policy [D]. Pittsburgh, PA: Department of Engineering and Public Policy, Carnegie Mellon University, 2008.
[9] COKER A K. Determine process-pipe sizes [J]. Chemical Engineering Progress, 1991, 87(3): 33-39.
Pipe Diameter Design and Analysis of Carbon Dioxide Pipeline Transportation Process
GAO Rui-min, ZHAO Xiao-lan, CHEN Guang-ying, LIANG Zhi-wu†, NA Yan-qing
(Hunan Provincial Key Laboratory for Cost-effective Utilization of Fossil Fuel Aimed at Reducing Carbon-dioxide Emissions,College of Chemistry & Chemical Engineering, Hunan Univ, Changsha,Hunan 410082,China)
According to the factors affecting the diameter size (i.e. mass flow rate, pipeline length and pressure drop), this article analyzed the pipeline design model of Rubin from the three aspects and established their corresponding numerical models. Furthermore, the reliabilities of the proposed numerical models were validated by another pipeline design model (i.e. the MIT model). Besides, the economic cost of CO2pipeline transportation was also estimated through the cost analysis of the total pipeline capital investment and the additional pressure station cost. The research result shows that: (i) the proposed models share the same variable change rules and numerical model types with the validation model, and (ii) all of them have high correlation with numerical models (their correlation coefficientsR2are larger than 0.970). The pipeline design and cost analysis proposed in this work have some reference value for the process design of CO2pipeline transportation.
numerical model; pipeline design; CO2; cost analysis
2014-12-21
国家科技支撑计划项目(2012BAC26B01)
高瑞民(1965-),男,河南濮阳人,高级工程师,湖南大学兼职教授
†通讯联系人,E-mail:zwliang@hnu.edu.cn
1674-2974(2015)12-0095-05
TQ022.1
A

