基于谐波合成法的大涡模拟脉动风场生成方法研究*

沈 炼 ,韩 艳† ,蔡春声,2 ,董国朝

(1. 长沙理工大学 土木与建筑学院，湖南 长沙 410114；2. 路易斯安那州立大学 土木与环境工程，美国路易斯安那州，巴吞鲁日 70803)

基于谐波合成法的大涡模拟脉动风场生成方法研究*

沈 炼1,韩 艳1†,蔡春声1,2,董国朝1

(1. 长沙理工大学 土木与建筑学院，湖南 长沙 410114；2. 路易斯安那州立大学 土木与环境工程，美国路易斯安那州，巴吞鲁日 70803)

为准确模拟大涡模拟入口处的脉动信息，在充分考虑脉动风场的功率谱、相关性、风剖面等参数前提下，运用谐波合成方法生成了满足目标风场湍流特性的随机序列数，通过对FLUENT软件平台进行二次开发，将生成的随机序列数赋给大涡模拟的入口边界，从而实现了大涡模拟的脉动输入.基于风洞试验数据，分别建立了两种模拟脉动风场的数值模型，一为没有任何障碍物的空风洞，运用谐波合成方法生成的随机序列数作为入口边界来生成脉动信息；二为与真实风洞一致的尖劈粗糙元风洞，采用平均风作为入口边界，利用尖劈粗糙元对风场的扰动来产生脉动信息.通过对比两种数值模型发现：基于谐波合成方法生成的脉动风场可作为大涡模拟的入口边界，可为大涡模拟脉动入口研究提供参考.

大涡模拟；谐波合成；数值模拟；脉动风场

大涡模拟在计算资源与计算效率方面是雷诺时均模拟(RANS)和直接模拟(DNS)的折中，集成了二者优势，因此在CFD模拟方面得到了广泛应用.但在实际运用过程中，大涡模拟入口边界处的脉动信息给定问题还没有得到完全解决[1].目前，许多学者直接将均匀来流赋给入口边界，没有考虑脉动信息的作用．而在实际风场中，来流脉动对结构的脉动风压和瞬时风荷载起着非常重要的作用[2]，有着不可忽略的地位.因此，非常有必要在大涡模拟过程中考虑脉动信息的影响.

针对大涡模拟脉动入口研究方法，可以将其分为三类[3]，第一类为“预前模拟法”，是运用一个预前模拟区域，将目标风场预先模拟出来，然后赋给主模拟区域的入口边界.朱伟亮等[2]在预前模拟区域用流场循环的方法生成了脉动风场，并对钝体平面屋盖的结构风压进行了模拟，这种脉动风场生成方法的不足之处是需要生成匹配的数据库，会消耗巨大的内存和计算时间.序列合成法的另一种储存形式是用空间序列储存，Chung[4]利用泰勒方法协调了预前模拟方法两个计算域之间的离散差异性，对槽道流进行了模拟，运用该方法的缺点是不同时刻的速度不能严格的由泰勒级数展开来获取，因此插值的效果不佳.第二类方法为涡方法，针对涡方法的研究，Mathey等[5]人用一系列的二维随机漩涡加载到平均风场中去从而得到脉动风场，这种方法生成的脉动风场虽然具有较好的空间相关性和湍动能信息，但不足之处是目标风场很难满足风场各向异性目标谱的要求.第三类方法为序列合成法，序列合成法是运用傅里叶变换的方法来生成脉动风速时程.2002年Hanna等[6]人提出了一种简单的各向异性湍流脉动生成方法，生成了随机正态序列数，它是假设在顺风方向和垂直方向的脉动均方根和平均速度有不同的比例，然后通过加权得到脉动信息，这种方法的不足是缺少了雷诺应力信息，同时湍流也会很快衰减.此后，2006年，Kondo[7]等提出了动态湍流输出方法，但这种方法不能满足目标谱的需求.2008年，Xie和Castro[8]用雷诺应力的垂向分布构造出了脉动速度分量，得到的脉动量满足湍流的基本特性并具有雷诺应力信息，但是生成的湍流在入口处并不满足连续性的需求，需要经过很长时间的发展才能形成真正的湍流.后来，Hemon and Santi[9],Huang等[10-11]也针对大涡模拟的入口脉动边界做出了相关研究，得到了不错的计算结果.

本文借助于经典的谐波合成方法，在充分考虑湍流的平均风剖面、目标谱、空间相关性等指标下，合成一系列的随机序列时程数据，把生成的时程数据与大涡模拟的入口建立对应关系，基于对FLUENT软件平台进行二次开发，把生成的随机序列数赋给大涡模拟的入口边界，从而生成入口脉动信息.最后通过对比数值模型和风洞试验结果发现：基于谐波合成的脉动信息生成方法能满足大涡模拟入口边界的要求，其优势在于目标谱及相关性参数能根据不同情况的需要进行随意调整，合成的时程数据可直接赋给入口边界，生成速度快，模拟时间长短可以随意控制，模拟的点都相互独立，可以很好地进行并行计算，大大提高计算效率.

1 数值模拟理论与方法

1.1 大涡模拟

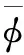
(1)

式中:D为流动区域，x'为实际流动区域里面的空间坐标，x是过滤后的大尺度空间坐标，G(x,x')是过滤函数[13]，表达式为：

(2)

式中：V是控制体积所占几何空间的大小，过滤后瞬态下的空间N-S方程可表示为：

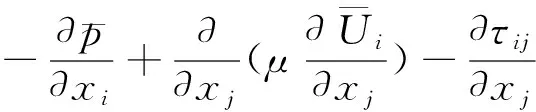
(3a)

(3b)

上式为动量守恒方程和质量守恒方程，其中带横线上标的量表示过滤后的可解尺度量，τij为亚格子尺度应力，具体表达式为：

(4)

为了封闭方程(3)，本文采用Smagorinsky亚格子模型，假定SGS应力形式为：

(5)

在求解方面，本文的N-S方程采用建立在交错网格上的SIMPLE方法进行求解，对流项和扩散项均采用二阶中心差分格式，时间导数采用二阶半隐式离散方法，用超松弛方法(SOR)求解压力Poisson方程，压力和动量松弛因子分别取0.3和0.7.

1.2 随机序列合成

(6)

式中：H(ω)为下三角矩阵；对角项为ω的实非负函数，非对角项通常为ω的复函数.

(7)

(8)

脉动风速的合成还需考虑平均风、功率谱、相关性和时间步长的影响.入口风速时程的平均速度采用指数率风剖面公式:

(9)

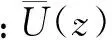
本文脉动风功率谱采用我国规范采用的Kaimal谱，其表达式为：

(10)

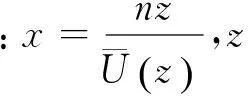
本文空间互相关性采用Davenport给定的经验公式[16]，如下所示：

(11)

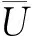
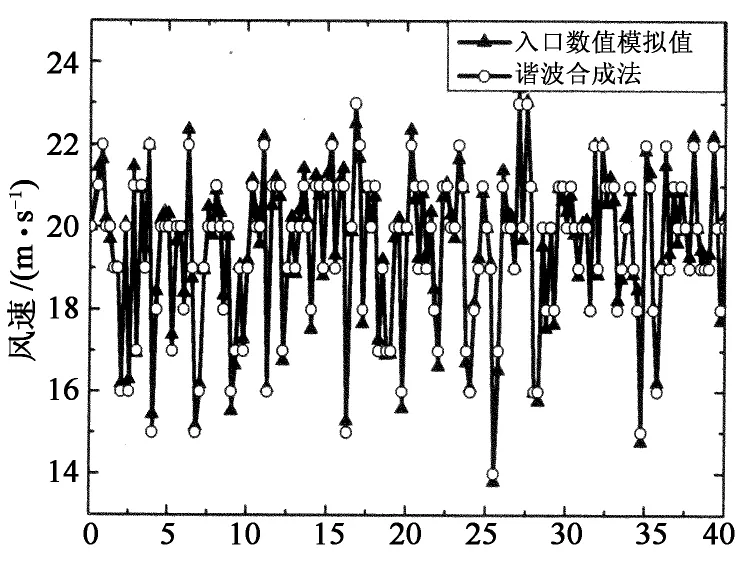
(12)

式中：Sii和Sjj分别为i,j两点的自谱密度函数.本文对随机序列数合成、UDF导入和大涡模拟3个过程采用了相同的时间步.在随机序列数合成过程中，为了防止频率的失真，时间步ΔT应该满足：

(13)

在UDF时程数据对接上，要保持计算步的统一，而在大涡模拟过程中，计算步长[17]应满足库朗数(CFL)要求，可表示为：

(14)

式中：U为风速；Δx为网格尺寸；ΔT为时间步长，为同时满足三方面的要求，时间步长取0.002 5 s.

在充分考虑脉动风场的平均速度、功率谱、相关性、时间步长等参数后，基于谐波合成理论，用MATLAB对风速时程数据进行合成，生成满足目标风场的随机序列数.然后将生成的随机序列数与入口网格在时间和空间上建立对应关系，时间上要满足时间步长的一致，保证谐波合成风速与大涡模拟风速在时间上的同步.空间上要对入口网格坐标进行严格控制，将模拟点的速度时程赋给对应的入口网格中心点，整个过程用UDF程序编制，对FLUENT软件用户自定义模块进行加载，重新定义入口速度，从而实现大涡模拟入口脉动信息的输入.

2 大涡模拟入口脉动风场特性分析

为验证本文入口处脉动信息输入的正确性，建立了一空风洞数值模型，里面没有任何障碍物，具体尺寸为15 m×2.5 m×3.0 m (x×y×z)，总网格数为180万.入口平均风采用指数率风剖面形式，α值为0.16，取基准风速为20 m/s，地表粗糙高度为0.05 m.入口脉动量由MATLAB程序模拟生成，然后通过UDF程序将这些时程数据赋给入口边界网格，待计算稳定后提取模型入口0.5 m和1 m高度处的风速时程并与输入的谐波合成法生成的数据序列对比，如图1～2所示.

时间/s

时间/s

由图1～2可以看出，模型入口监测值与输入的谐波合成法生成的数据序列基本一致，说明了入口边界风速时程输入方法的正确性.为了验证入口边界功率谱的正确性，将数值模型入口1 m高度处顺风方向功率谱模拟值与我国规范进行对比，如图3所示.

频率/(rad·s-1)(对数坐标)

从图3可以看出，功率谱能较好的与我国规范采用的Kaimal谱吻合，满足脉动风场特性要求.

对流场入口中心0.5 m和1 m高度处的速度时程数据进行相关性分析，定义两点分别为A和B.图4给出了入口监测点A和B的互相关性和B点的自相关性检验结果，图4(a)中目标值由公式(11)给出.

时间/s

时间/s

图4表明了入口处脉动风场相关性呈指数率衰减，模拟值与理论目标值衰减趋势一致，体现出了模拟风场在入口处具有良好的相关性.

通过对上述平均风速、功率谱、相关性等参数进行分析，发现基于谐波合成法生成的脉动风场满足湍流的基本特性，可以在大涡模拟的入口进行无缝对接.

3 数值模型

为验证数值模型内部风场正确性，以TJ-2风洞试验数据[18]为参照对象，建立了两个数值模型，一为没有任何障碍物的空风洞，与第二节所用空风洞验证模型为同一计算模型，利用上节所提出的谐波合成方法来生成入口脉动信息，简称为“空风洞数值模型”；二为与风洞试验条件一致的“尖劈粗糙元数值模型”.下面分别对两种模型的尺寸，网格数量，计算参数与边界条件进行介绍.

3.1 模型尺寸与网格数量

3.1.1 空风洞数值模型

TJ-2风洞具体尺寸为15 m×2.5 m×3.0 m (长×高×宽)，空风洞数值模拟采用与物理风洞一致的模型尺寸，为保证计算精度，采用全六面体网格，并对总网格数为90万、180万、400万3种网格进行了网格无关性测试，权衡计算资源和计算精度后，选取了180万网格数模型作为最终计算模型，网格在模型底部进行加密，增长因子为1.1，最底层网格高度为0.01 m，具体网格如图5所示.

图5 空风洞数值模型网格示意图

3.1.2 尖劈粗糙元数值模型

尖劈粗糙元数值模型与物理风洞试验条件保持一致，布置如图6所示.与上一节类似，为保证精度，对尖劈粗糙元数值模型进行全场六面体网格划分，并对260万，450万，800万3种网格进行了网格无关性测试，无关性测试结果如表1所示.

通过比较模型内部测量中心处湍流度发现260万网格数模型较450万和800万的偏差较大，但450万和800万网格数的计算结果偏差幅度很小，权衡计算精度和计算资源的影响后，最终选取了450万网格数作为最终计算网格.整个网格在底部进行加密，最底层网格高度为0.005 m，延伸率为1.1，网格如图7所示.计算过程中，对空风洞数值模型和尖劈粗糙元数值模型的“预定模型中心”位置进行风速监测，具体位置如图6所示.

表1 网格无关性检验

Tab．1 Test of the grid dependence

网格数量260万450万800万湍流度9.9%12.42%12.49%

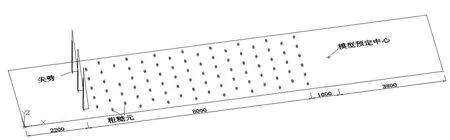
图6 尖劈粗糙元模型尺寸示意图

图7 尖劈粗糙元数值模型网格示意图

3.2 边界条件设置

空风洞数值模型的入口条件是基于对FLUENT软件平台进行二次开发，将生成的随机序列数赋给入口边界；而尖劈粗糙元数值模型则采用平均风作为入口边界，详细边界条件与计算参数如表2所示.

4 计算结果

空风洞数值模型采用超线程12核工作站进行计算，模拟150 s时长(60 000步)需耗时60 h，其计算结果如图8(a)所示.尖劈粗糙元模型同样采用超线程工作站进行计算，模拟同样时长需耗时124 h，计算结果如图8(b)所示.

表2 计算参数与边界条件

Tab．2 Computational parameters and boundary conditions

计算参数空风洞模型尖劈粗糙元模型湍流模型大涡模拟大涡模拟网格类型六面体结构网格六面体结构网格入口边界UDF导入的随机序列数均匀来流,U=20m/s计算域侧面对称边界对称边界计算域顶面自由滑移自由滑移计算域底面无滑移固壁无滑移固壁尖劈粗糙元表面无滑移固壁无滑移固壁

(a) 空风洞数值模型计算云图

(b)尖劈粗糙元数值模型计算云图

通过对 “预定模型中心”不同高度处的风速监测，得到监测中心处的平均风剖面与湍流度信息，对其无量纲处理并与风洞试验结果进行对比，其结果如下图所示.通过比较图9和图10发现，在风剖面和湍流度方面，两种数值模型相对风洞试验值的偏差均较小，能满足工程精度需要，也再一次证明了谐波合成方法生成脉动风场的正确性.用最小二乘法对空风洞模型风剖面进行指数率拟合，得到α指数为0.161，非常接近风洞试验的拟合值0.162，也接近于我国规范给出的B类风场特性.

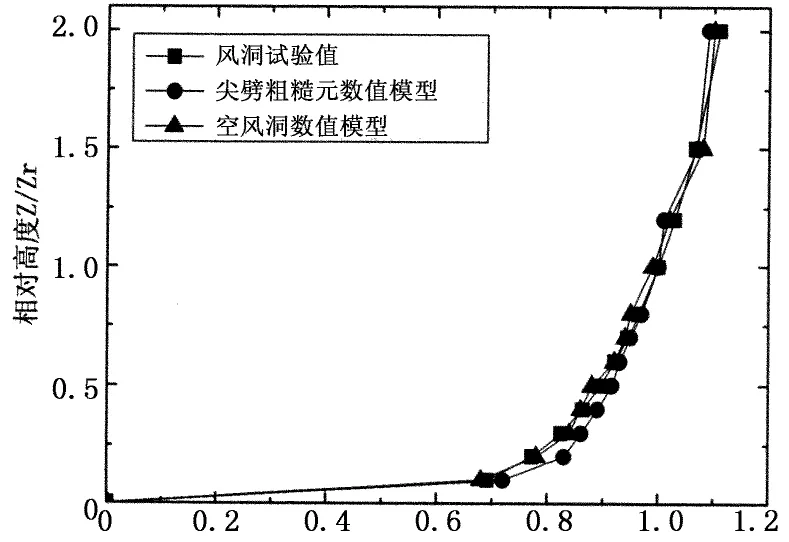
相对风速U/Ur

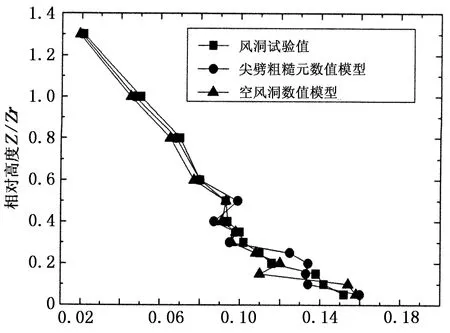
湍流度Iu

对“预定模型中心处”1 m高度处的时程数据进行分析，得到空风洞模型和尖劈粗糙元模型的顺风方向功率谱，将其进行拟合并与Kaimal谱进行对比，如图11所示.

频率/Hz

通过对两种方法同一监测点顺风方向功率谱与Kaimal谱进行对比发现，数值模拟结果与风洞试验的风速功率谱在低频段(频率<1)吻合较好，但在高频段(频率>1)出现陡降，而工程领域最为关心的频率出现在惯性子区(0.2<频率<1)，本文两种数值模拟方法均能较好的捕捉该区域的风谱，因此所生成的脉动风能较好的满足工程需要.目前，数值模拟的风速时程普遍存在风谱高频段衰减现象，是由于高频段代表风场中小涡的能量贡献，而LES中小尺度涡是用亚格子模型进行封闭，不能直接对小尺度涡进行求解，因此数值模拟不能捕捉到脉动风场的高频段风谱，通过改进湍流模型和加密网格数量可以改善风谱高频衰减问题.

在计算效率方面，将两种数值模型所需的网格数和耗时量作出对比，如表3所示.

表3 计算效率对比

Tab．3 Efficiency of the computational

模型网格数/万计算时间/h空风洞模型18060尖劈粗糙元模型450124

由表3可以发现，在达到允许精度要求下，空风洞模型所需的网格数不到尖劈粗糙元模型的一半，计算耗时量方面也远远优于尖劈粗糙元模型.

此外，空风洞数值模型具有更好的适应性，特别是对不同脉动风场的模拟，空风洞模型只需对目标风场的特性参数进行调整，操作简单方便，可调性强.而尖劈粗糙元数值模型只能通过不断调整尖劈粗糙元的位置和数量来对目标风场进行试算，计算工作量大，消耗时间长.

5 结 论

本文基于谐波合成方法生成了随机序列数，通过对商业软件FLUENT进行二次开发，利用UDF程序把时程数据转化成大涡模拟的入口脉动信息，同时建立了与物理风洞试验条件一致的尖劈粗糙元数值模型，通过对比研究得到了以下成果和结论.

1)实现了随机序列数在大涡模拟入口处的无缝对接，开发了大涡模拟入口脉动速度输入模块，可以很好地进行并行计算，解决了大涡模拟入口处湍流信息给定问题.

2)通过比较平均风剖面、湍流度和功率谱等结果发现：基于谐波合成方法生成的大涡模拟脉动风场具有较高的精度，能满足工程需要，但风速功率谱在高频段会出现衰减现象.

3)通过对比空风洞数值模型和尖劈粗糙元模型的计算效率发现，空风洞数值模型在网格数量和计算耗时方面均要远远优于尖劈粗糙元数值模型.

4)相比尖劈粗糙元数值模型，基于谐波合成脉动生成方法对不同风场模拟只需调整风场特性参数，操作方便，模拟速度快，是一种极具前景的脉动生成方法，也可为大涡模拟入口处脉动生成方法精细化研究提供参考.

基于谐波合成法的脉动风场生成方法是谱合成方法的一种拓展，拥有许多优点的同时也存在一些不足，如生成的随机风速时程不满足N-S方程的连续性，风谱高频衰减等问题还有待进一步解决.

[1] JIANG Wei-mei，MIAO Shi-guang. 30 years review and perspective of the research on the large eddy simulation and atmospheric boundary layer[J]. Advances in Nature Sciences, 2004, 14: 11-19.

[2] 朱伟亮，杨庆山. 基于 LES 模型的近地脉动风场数值模拟[J]. 工程力学，2010，27(9)：17-21.

ZHU Wei-liang, YANG Qing-shan. Large eddy simulation of near ground turbulent wind field [J]. Engineering Mechanics, 2010, 27 (9): 17-21. (In Chinese)

[3] BABA-AHMADI M H, TABOR G. Inlet conditions for LES using mapping and feedback control[J]. Computer & Fluid, 2009, 38(6): 1229-1311.

[4] CHUNG Y M, SUNG H J. Comparative study of inflow conditions for spatially evolving simulation[J]. AIAA Journal, 1997, 35(2): 269-274.

[5] MATHEY F, COKLJAT D, BERTOGLIO J P,etal. Assessment of the vortex method for large eddy simulation inlet conditions[J]. Progress in Computational Fluid Dynamics, 2006, 6: 1-3.

[6] HANNA S R, TEHRANIAN S, CARISSIMO B,etal. Comparisons of model simulations with observations of mean flow and turbulence within simple obstacle arrays[J]. Atmospheric Environment, 2002, 36: 5067-5079.

[7] KONDO H, ASAHI K, TOMIZUKA T,etal. Numerical analysis of diffusion around a suspended expressway by a multi-scale CFD model[J]. Atmospheric Environment, 2006, 40: 2852-2859.

[8] XIE Z T, CASTRO I P. Efficient generation of inflow conditions for large eddy simulation of street-scale flows[J]. Flow Turbulence and Combustion, 2008, 81: 449-470.

[9] HEMON P, SANTI F. Simulation of a spatially correlated turbulent velocity field using biorthogonal decomposition[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95 (1): 21-29.

[10]HUANG S H, LI Q S, WU J R. A general inflow turbulence generator for large eddy simulation[J]. Journal of Wind Engineering and Industrial, 2010, 98: 600-617.

[11]卢春玲，李秋胜，黄生洪，等. 大跨度屋盖风荷载的大涡模拟研究[J]. 湖南大学学报：自然科学版，2010，37(10):7-12.

LU Chun-ling, LI Qiu-sheng, HUANG Sheng-hong,etal. Large eddy simulation of wind loads on long-span roofs[J]. Journal of Hunan University : Natural Sciences, 2010,37 (10): 7-12. (In Chinese)

[12]DEARDOFF J W. The use of sub grid transport equation in a three dimensional model of atmospheric turbulence[J]. ASME Journal of Fluid Engineering, 1973, 95: 429-438.

[13]祝志文，陈魏，向泽，等. 大跨度斜拉桥主梁气动力特性的大涡模拟[J]. 湖南大学学报：自然科学版，2013，40(11): 26-33.

ZHU Zhi-wen, CHEN Wei, XIANG Ze,etal. Large eddy simulation of aerodynamics on main girder of long span cable-stayed bridges[J]. Journal of Hunan University: Nature Sciences, 2013, 40 (11): 26-33. (In Chinese)

[14]王福军. 计算流体动力学分析[M].北京：清华大学出版社，2004.

WANG Fu-jun. Computational fluid dynamics analysis [M]. Beijing: Tsinghua University Press, 2004. (In Chinese)

[15]JCR H, WRAY A, MOIN P. Eddies, streams, and convergence zones in turbulent flows[R]. Center for turbulence research report CTR-S88, 1988: 193-208.

[16]韩艳. 桥梁结构复气动导纳函数与抖振精细化研究[D]. 长沙：湖南大学土木工程学院，2007.

HAN Yan. Study on complex aerodynamic admittance functions and refined analysis of buffeting response of bridge[D]. Changsha: College of Civil Engineering, Hunan Univ, 2007. (In Chinese)

[17]Fluent Inc. Fluent user's guide, version：ansys12.0 [M]. USA：Fluent Inc Lebanon, 2009.

[18]庞加斌，林志兴. 关于风洞中用尖劈和粗糙元模拟大气边界层的讨论[J]. 流体力学实验与测量，2004，18(2)：32-37.

PANG Jia-bin, LIN Zhi-xing. Discussion on the simulation of atmospheric boundary layer with spires and roughness elements in wind tunnels[J]. Experiments and Measurements in Fluid Mechanics, 2004, 18(2): 32-37. (In Chinese)

Research on Generating Method of Fluctuating Wind Field of LES Based on WAWS

SHEN Lian1，HAN Yan1†, CAI Chun-sheng1, 2, DONG Guo-chao1

(1. School of Civil Engineering and Architecture，Changsha Univ of Science Technology，Changsha,Hunan 410114，China; 2.Department of Civil and Environmental Engineering，Louisiana State Univ，Baton Rouge，USA，LA 70803)

In order to accurately simulate the inlet boundary conditions of turbulence information of Large Eddy Simulation (LES), the fluctuating time-history data satisfying the target wind field were simulated with the weighted amplitude wave superposition (WAWS) considering the integral scale, power spectrum, turbulence intensity and wind velocity profile. The fluctuating time-history data were given to the inlet boundary of LES by the secondary development of the commercial software FLUENT. Consequently, the fluctuating information of the Large Eddy Simulation was obtained. The two numerical models were established on the basis of the experiment data in the wind tunnel. The first was the flow field without any obstacles in which the fluctuating time-history data simulated by WAWS method were the inlet boundary condition. The second was the flow field with spires and roughness element model in accordance with those in the wind tunnel, in which the mean wind velocity was given to the inlet boundary and the wind turbulences were generated by the spires and roughness elements. The results show that fluctuating wind field based on the WAWS method can be the inlet boundary for the LES and provides a reference for the investigation of the inlet boundary conditions of LES.

Large Eddy Simulation；weighted amplitude wave superposition；numerical simulation；fluctuating wind field

2014-11-11

国家重点基础研究计划(973计划)(2015CB057700)；国家自然科学基金资助项目(51408061，51178066，51278069)，National Natural Science Foundation of China(51408061，51178066，51278069) ；交通部西部交通科技项目重大科技专项资助项目(2011318824140)；长沙理工大学桥梁工程安全控制省部共建教育部重点实验室开放基金资助项目(12KB01)；湖南省研究生创新项目(CX2014B375)

沈 炼(1988-)，男，湖南岳阳人，长沙理工大学博士研究生

†通讯联系人，E-mail:ce_hanyan@163.com

1674-2974(2015)11-0064-08

O35

A