圆钢管混凝土短柱局压力学性能研究*

刘 劲，丁发兴，龚永智†，余志武,2，李大稳

(1.中南大学 土木工程学院，湖南 长沙 410075： 2.高速铁路建造技术国家工程实验室，湖南 长沙 410075)

圆钢管混凝土短柱局压力学性能研究*

刘 劲1，丁发兴1，龚永智1†，余志武1,2，李大稳1

(1.中南大学 土木工程学院，湖南 长沙 410075： 2.高速铁路建造技术国家工程实验室，湖南 长沙 410075)

进行了12个圆钢管混凝土短柱局压试验，探讨混凝土强度等级、局压面积比对钢管混凝土短柱局压极限承载力的影响.试验结果表明，混凝土强度等级提高，极限承载力增大而延性降低；局压面积比减小，则承载力越高延性越低.采用合理的材料本构关系，利用ABAQUS有限元软件建立圆钢管混凝土短柱局压的壳-实体三维有限元模型，在试验验证的基础之上，利用ABAQUS软件及相应的有限元模型探讨局压面积比、含钢率、钢材强度和混凝土强度对短柱局压极限承载力的影响.通过拟合分析提出圆钢管混凝土短柱局压极限承载力的实用计算公式，将该计算公式、有限元计算值、其他学者提出的计算公式与笔者试验及其他学者共47组圆钢管混凝土短柱局压试验资料进行对比，分析结果表明，笔者提出的公式计算结果与试验结果相比具有较高的精度.

钢管混凝土；局压；有限元方法; 极限承载力

与传统的钢结构或混凝土结构相比，钢管混凝土柱具有承载力高、延性好和施工便捷等优点，在建筑和桥梁工程中得到了越来越广泛的应用[1]，为此许多学者对此开展了研究[1-6].钢管混凝土柱局部受压是工程使用中常见的一种受力方式，如在桥墩结构中.蔡绍怀[1]进行了圆钢管混凝土中心区局部承压试验，探讨了圆钢管混凝土试件长度、套箍指标、局压面积比和在局压区域配置螺旋箍筋对局压性能的影响和对局压极限承载力的提高作用．作者根据试验测试结果，采用回归分析方法得到圆钢管混凝土局压极限承载力计算公式，其研究成果为钢管混凝土结构技术规程 (CECS28:2012)[7-8]所采纳.Han等[2～4]对圆钢管混凝土柱局部受压下的工作机理进行了研究，结果表明：端板厚度和局压面积比对试件承载力及延性有很大的影响，同时截面形式的不同也对试件中钢管与混凝土的套箍作用有显著影响；并运用ABAQUS软件对钢管混凝土短柱局压进行分析，提出钢管混凝土短柱局压承载力的简化计算方法.

笔者所在课题组采用ABAQUS软件选取合理的材料本构关系和壳-实体三维有限元建模方法对圆形及圆端形钢管混凝土轴压短柱进行分析[9-10]，可合理体现钢管对混凝土约束套箍作用，能准确模拟钢管混凝土轴压短柱的力学性能，该方法可进一步应用于圆钢管混凝土短柱局压力学性能分析中.为丰富圆钢管混凝土短柱局压力学性能的研究，提出更为简洁、准确的承载力公式，本文展开如下工

作：1)进行12个无端板圆钢管混凝土短柱局压试验研究；2)运用ABAQUS有限元软件建立三维有限元模型，对圆钢管混凝土短柱局压进行建模计算；3)探讨混凝土强度、局压面积比、含钢率以及钢材强度对圆钢管混凝土短柱局压极限承载力的影响；4)通过拟合建立圆钢管混凝土短柱局压承载力实用计算公式，根据本文及其他学者提供的试验成果，比较笔者提出的计算式与其他计算式之间的精度差异.

1 试验研究

1.1 试验概况

试验共设计了12个圆钢管混凝土试件，名义尺寸为D×t×L=300 mm×4 mm×900 mm，试件信息见表1.其中D为截面直径，t为钢管壁厚，L为试件高度，d为圆钢管混凝土试件局压加载板的直径，fcu为混凝土立方体抗压强度，fy为钢材屈服强度，β为局压面积比，β=Ac/Ab(Ac为试件混凝土横截面面积，Ab为局压面面积).

为方便观察试件加载破坏的变形，在加工好的空钢管试件外表面喷上红色油漆，并画好50 mm×50 mm白色网格.浇筑混凝土时，对灌入的混凝土振捣密实，浇灌混凝土结束后，使顶端混凝土表面与钢管上截面保持水平，浇灌时，制作150 mm×150 mm×150 mm混凝土立方体试块，并将其与钢管混凝土试件在同等条件下养护.

表1 钢管混凝土短柱局压试件一览表

Tab.1 Geometric properties and characteristics of CFT stub specimens

序号试件编号D×t×L/(mm×mm×mm)加载方式d/mmfy/MPafcu/MPaβNb,e/kNNb,FE/kNNb,f/kN1CLST1-A300×3.72×900圆形局压10031135.58.851820196419082CLST1-B300×3.76×900圆形局压10031135.58.851800196419223CLST2-A300×3.70×900圆形局压20031135.52.143310307328564CLST2-B300×3.68×900圆形局压20031135.52.143200307328485C1-A300×3.70×900全截面受压30031135.50.953780333936256C1-B300×3.71×900全截面受压30031135.50.953500333936307CLST3-A300×3.69×900圆形局压10031154.48.852010222722558CLST3-B300×3.76×900圆形局压10031154.48.852020222722819CLST4-A300×3.70×900圆形局压20031154.42.1438103904362010CLST4-B300×3.77×900圆形局压20031154.42.1439503904365111C2-A300×3.74×900全截面受压30031154.40.9548964640497712C2-B300×3.87×900全截面受压30031154.40.95497646404851

1.2 试验方法

试验前，先测试钢材和混凝土的力学性能.钢材屈服强度fy为311 MPa，极限强度fu为460 MPa，弹性模量Es为2.07×105MPa.C30混凝土强度fcu为35.5 MPa，C50混凝土强度fcu为54.4 MPa.

将40 mm厚的局压垫板放置在试件顶端正中位置，试验荷载通过局压垫板传递.两个位移计布置在压力机的上下加载板之间，由此可测得局压垫板相对于试件的位移，试件上作用的压力值可由机器直接读出.为考察钢管与混凝土之间粘结，同时准确地观测钢管的变形，对于每个试件，钢板从上至下截面处布置5个应变花.应变花、位移计和钢管混凝土试件加载如图1所示.

试验采用如下加载机制：弹性阶段加载时，每级荷载相当于极限荷载的1/15左右，弹塑性阶段加载时，每级荷载相当于极限荷载的1/25左右，每级荷载持续时间约为3 min，加载过程保持慢速连续，相应数据同步采集，试件接近极限承载力时，慢速连续加载直至试件破坏，每个钢管混凝土试件试验时间持续约2 h.

图1 试验装置图

1.3 试验现象

在加载初期，圆钢管混凝土试件处于弹性工作状态，荷载达到极限荷载的60%～70%以前，荷载-位移曲线大致呈线性关系，试件表面没有明显变化.随着荷载的增加，当荷载增至极限荷载的60%～70%时，试件开始进入弹塑性阶段，其轴向刚度不断减小，试件实测的荷载-轴向位移曲线如图2所示，不同荷载水平下试件表面的钢管纵向应变(εL)和环向应变(εθ,s)分布如图3所示.此时试件表面开始出现鼓曲，局部受压使得钢管膨胀现象从上到下依次递减.随着外荷载的继续增加，当试件达到极限荷载后，钢管变形尤其是试件上端迅速增加，端部混凝土明显压碎开裂，试件破坏如图4所示.

Δ/mm

Δ/mm

图3 试件纵环向应变图

除局压面积比为8.55的圆钢管混凝土试件之外，其余试件破坏后承载力出现较明显下降，如图2所示，最后试件因为变形过大而终止试验.由图可知，钢管混凝土试件在加载作用下呈向外鼓出现象，试件破坏形态受局压面积比影响显著，局压面积比越小，鼓出范围和程度越大.

1.4 试验结果分析

由图2钢管混凝土局压试件荷载-位移曲线可知，局压面积比对试件承载力和刚度有着很大的影响，试件承载力和刚度随着局压面积比的增大而递减,同时，局压面积比越大，其下降趋势越缓.

图3为不同加荷阶段(n=N/Nb分别为0.1,0.3,0.5,0.7和0.9，Nb为短柱局压极限承载力)钢管纵向、环向应变沿高度的分布情况.从图中可以看出，在荷载的初始阶段，纵向、环向应变增加较慢，当荷载达到极限荷载70%以上，应变迅速增加，试件中上部环向应变和纵向应变最大，与试验所观察到的鼓曲情况相吻合.

为了比较圆钢管混凝土短柱局压约束效果，引入钢管混凝土短柱局压承载力折减系数SI，即钢管混凝土短柱局压极限承载力Nb,e与试件全截面受压极限承载力Nu,e的比值：

(1)

图5为本文12个试件的SI和β的对比图(试件相同的取平均比值)，可见，SI值随β增长而降低，对于不同混凝土等级，在相同β值时，C30圆钢管混凝土短柱比C50圆钢管混凝土短柱具有更高的SI值.

图4 不同局压比试件破坏形态对比图

β

为了比较圆钢管混凝土短柱局压延性性能，引入钢管混凝土短柱局压承载力延性系数DI：

(2)

式中:Δb,e为钢管混凝土短柱局压极限承载力Nb,e对应的位移;Δ85%为局压试件达到极限承载力后下降至85%Nb,e所对应的位移值.

图6为本文12个局压试件的DI和β的对比图(试件相同的取平均比值)，可见，DI值随β增大而增大，即局压面积比越大，钢管混凝土短柱局压延性越好，β=8.55时，圆钢管混凝土没有下降段.

β

2 理论分析

2.1 建立模型

以ABAQUS/Standard6.4[11]为有限元分析工具建立模型，钢管采用壳单元(S4R)，局压加载板、混凝土和钢管端部垫板采用三维实体单元(C3D8R)，模型中单元网格划分形式为Structured，如图7所示.模型中钢管与混凝土的界面采用库伦摩擦型接触，切线方向采用罚函数，摩擦系数取0.5，法线方向选择硬接触模拟，相互作用为表面-表面接触，滑移方式为有限滑移，参数取值及建模方法参考文献[9-10].

图7 模型网格划分

钢材和混凝土的本构关系及相应的参数取值见文献[10]，混凝土与端部垫板、混凝土与局压加载板的约束形式为绑定,通过壳-实体耦合以定义钢管与其端部垫板的约束关系.模型中一端垫板固定,另一端在局压加载板上加载.采用位移方式加载以得到荷载-位移曲线的下降段,并通过增量法求解.

2.2 计算结果分析

选取本文试验及文献[1-2]中的47组圆钢管混凝土短柱局压试验结果进行有限元分析，采用上述有限元理论建立模型，计算得到不同局压面积比圆钢管混凝土典型破坏形态如图8所示.

荷载-位移曲线有限元计算结果与试验结果的比较如图9所示，本文有限元结果Nb,FE与试验结果Nb,e如表1所示，试验结果与有限元结果比值的均值为1.006，离散系数为0.077，可见有限元计算结果与试验结果整体吻合较好.

图8 破坏形态

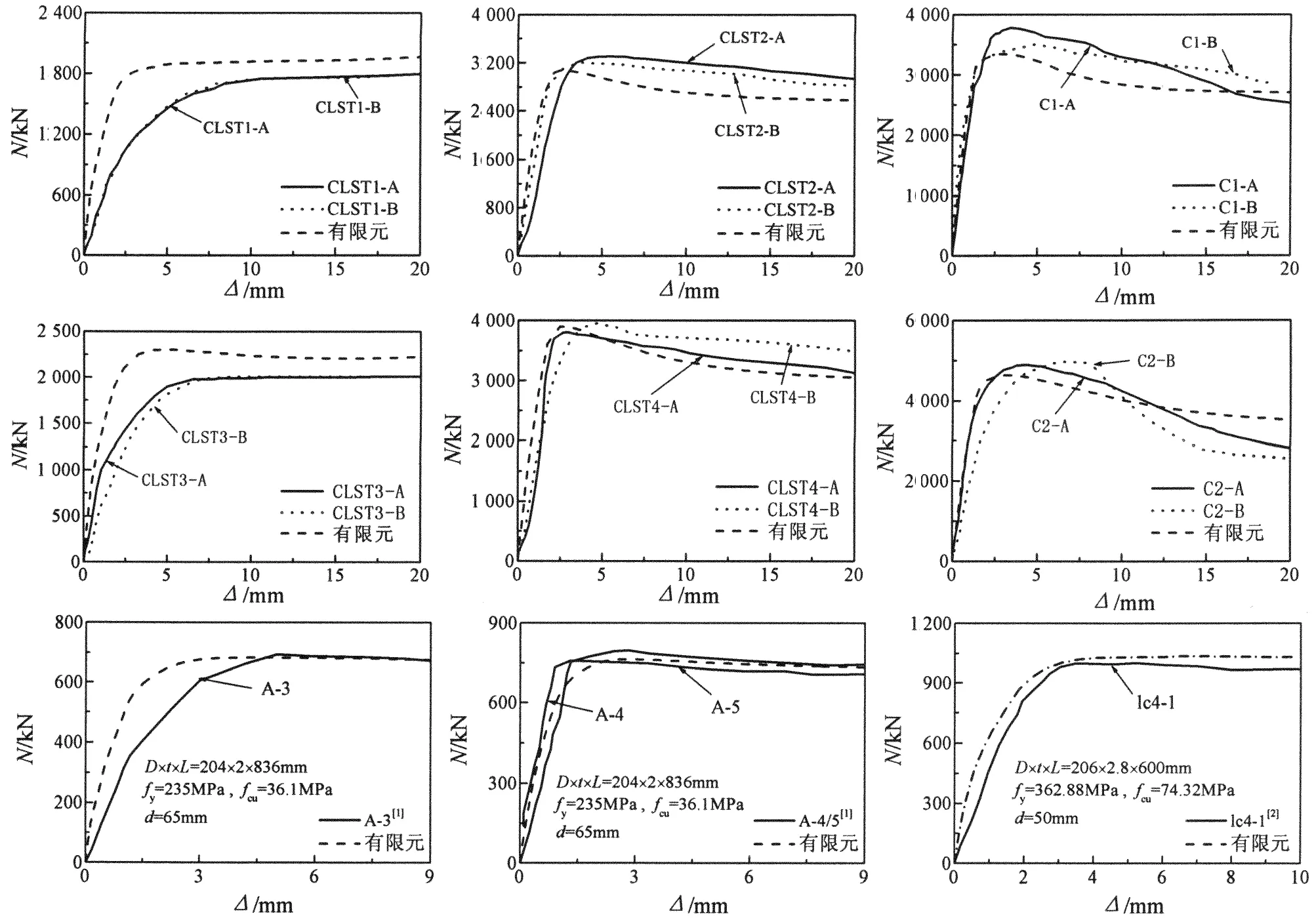
图9 局压试验结果与有限元计算结果比较

2.3 加载板形状对荷载-位移曲线的影响

采用与本文相同的试验参数，改变加载板形状，与试验作相同局压面积比的对比，即圆钢管混凝土柱通过方形加载板加载，探讨加载板形状对荷载-位移曲线的影响.典型荷载-位移曲线如图10所示.可见，β=8.55时，圆钢管混凝土柱采用圆方加载板试件荷载相差在1%以内，β=2.14时，圆钢管混凝土柱采用方加载板试件极限承载力高于采用圆加载板试件4.98%.可见，加载板形状的改变对试件荷载-位移曲线影响较小.

Δ/mm

2.4 荷载-位移曲线参数分析

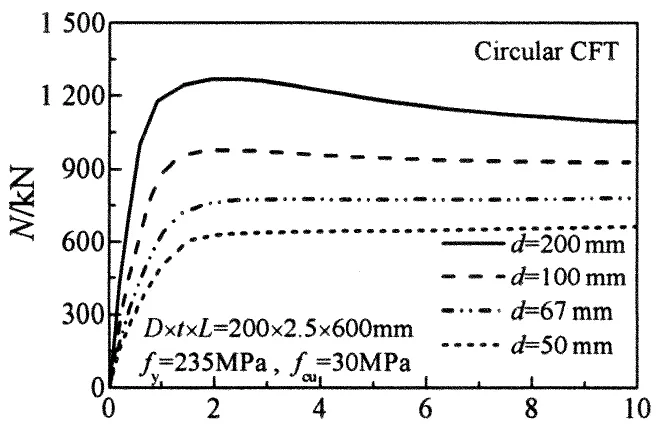
考虑局压面积比β，含钢率ρ，钢材强度fy，混凝土强度fcu等因素的影响，对钢管混凝土局压性能进行有限元参数分析．模型情况：圆钢管混凝土短柱84组，直径D均为200 mm，钢管壁厚t分别为2.5 mm，4.9 mm，7.2 mm，钢管长L为600 mm.局压面积比β分别为16, 9, 4, 1，混凝土抗压强度fcu分别为30 MPa,70 MPa,100 MPa,钢材屈服强度fy分别为235 MPa,335 MPa,420 MPa,其中Q235钢材匹配C30混凝土和C70混凝土,Q335钢材匹配C70混凝土和C100混凝土，Q420钢材匹配C70混凝土和C100混凝土,典型荷载-位移曲线如图11所示.

1) 局压面积比：图11(a)为圆钢管混凝土短柱在不同局压面积比下的荷载-位移曲线对比.从图11(a)可知局压面积比对钢管混凝土短柱局压极限承载力影响很大,局压面积比越大,极限承载力越小.

2) 含钢率：图11(b)所示为圆钢管混凝土短柱局压在不同含钢率下的荷载-位移曲线比较.从图11(b)可知，当含钢率较大时，构件弹性阶段的刚度和极限承载力更大.当含钢率达到一定阶段时，构件的荷载-位移曲线没有下降段.

3) 钢材强度：图11(c)所示为圆钢管混凝土短柱局压在不同钢材强度下的荷载-位移曲线比较.从图11(c)可知，钢材强度越大，构件极限承载力越大，但构件弹性阶段的刚度没有增大.

4) 混凝土强度：图11(d)所示为圆钢管混凝土短柱局压在不同混凝土强度下荷载-位移曲线的比较.从图11(d)可知，混凝土强度越大，构件极限承载力和构件刚度越大.

Δ/mm

Δ/mm

Δ/mm

Δ/mm

2.5 极限承载力影响因素参数分析

根据文献[5]，圆钢管混凝土短柱轴压承载力Nu可定义为：

Nu=fcAc(1+kФ)．

(3)

式中：Ac为混凝土截面面积；k为套箍系数(k=1.7)；Ф为套箍指标，Ф=fyAs/fcAc.

假设局压面积Ab下圆钢管混凝土短柱局压承载力计算公式为：

Nb=Kb(1+kФ)fcAb．

(4)

式中：Kb为圆钢管混凝土短柱局压承载力影响系数.

影响局压承载力影响系数Kb的主要因素有局压面积比、含钢率、钢材强度和混凝土强度.图12所示为各个参数对局压承载力影响系数的影响.从图中可知：局压面积比是影响局压极限承载力最重要的参数，局压面积比越大，局压影响系数Kb越大.

图12 局压比和其他参数对钢管混凝土短柱局压承载力影响系数Kb的影响

3 短柱局压承载力实用计算公式

3.1 公式的提出

通过参数分析可知Kb与套箍指标Ф和局压面积比β成一定的函数关系，对于圆钢管混凝土短柱局压，通过拟合可得：

(5)

对于圆钢管混凝土短柱局压承载力计算公式，式(4)可改写为：

(6)

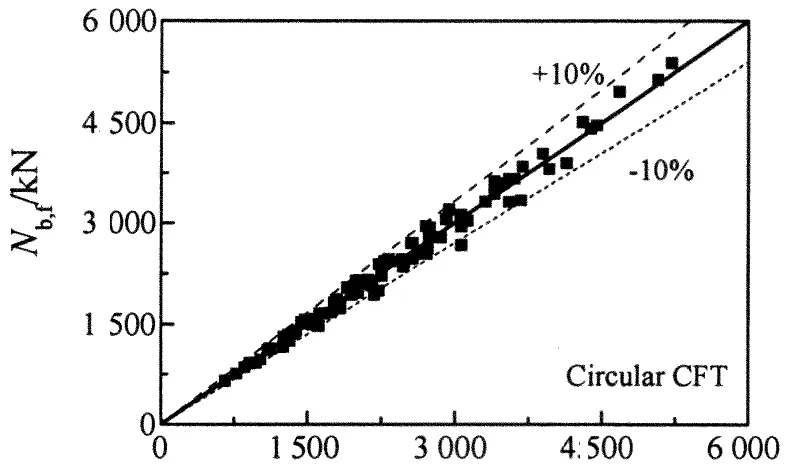
84组参数分析中有限元计算结果Nb,FE与承载力公式(6)计算结果Nb,f的比较如图13所示，两者吻合较好，差值大多在10%以内.

Nb,FE/kN

3.2 各种计算公式的比较

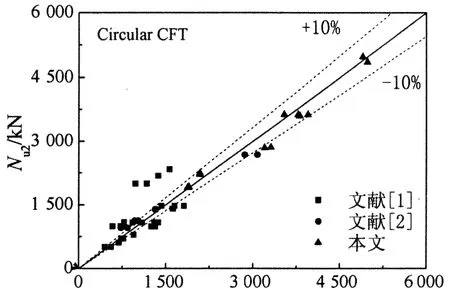
表1列出本文试件的试验结果，Nb,e为试验值，Nb,FE为有限元结果，Nb,f为式(6)计算结果.表2列出了不同学者及规范关于钢管混凝土短柱局压承载力的计算公式.图14所示为笔者提出的式(6)计算结果与试验结果的对比.

表2 短柱局压承载力实用计算公式

Tab.2 Formulas for ultimate bearing capacity of CFT stub columns under local compression

序号参考文献承载力计算公式1[1]Ф≤1.235;Nb,f=Acfc(1+2Ф)β0.5;fc=0.67fcuФ>1.235;Nb,f=Acfc(1+1.1Ф+Ф0.5)β0.5(7)2[4]Nb,f=KbNu;Kb=Aβ+Bβ0.5+C;Nu=Acfc(1.14+1.02Ф);A=(-0.18Ф3+1.95p2-6.89Ф+6.94)/100;B=(1.36Ф3-13.92Ф2+45.77Ф+60.55)/100;C=(-Ф3+10Ф2-33.2Ф+150)/100;(8)3[7-8]Ф≤e;Nb,f=0.9Acfc(1+fФ)β0.5;Ф>e;Nb,f=0.9Acfc(1+Ф+Ф0.5)β0.5混凝土等级

表3所示为圆钢管混凝土短柱局压极限承载力试验结果、有限元计算结果、式(6)～(9)计算结果的对比，表3中Nb,e为试验值，Nb,c为有限元及各公式的计算结果，可见有限元计算结果精度最高，离散性最小，式(9)由于混凝土抗压强度采用设计值，所以其计算结果最小，偏于保守.式(6)～(8)中，式(6)具有最高的计算精度，与式(7)和式(8)相比，表达形式更为简洁.

表3 短柱局压承载力试验结果与计算结果的对比

Tab.3 CFT stub columns comparison between calculated results and tested ones

样本数和参考文献统计特征值Nb,e/Nb,c有限元式(6)式(7)式(8)式(9)12[本文]均值1.0061.0131.1891.1371.981离散系数0.0770.0840.1370.0700.14027[1]均值1.0360.9561.2860.9962.076离散系数0.1680.2660.1830.3410.1858[2]均值0.9620.9121.3331.1342.430离散系数0.0910.1600.0660.0820.06647[合计]均值1.0160.9681.2691.0552.112离散系数0.1410.2100.1610.2560.170

Nb,c/kN

4 结 论

1)本文进行了12组圆钢管混凝土短柱局压试验研究，探讨局压面积比、混凝土强度对局压承载力的影响，结果表明局压面积比越大局压承载力越小，混凝土强度等级越高局压承载力越大.

2)运用有限元软件ABAQUS建立圆钢管混凝土短柱局压计算模型，计算结果与试验结果吻合良好且精度最高.

3)有限元参数分析表明影响圆钢管混凝土短柱局压承载力的主要因素有局压面积比、含钢率、钢材强度和混凝土强度，局压面积比是影响局压极限承载力的主要因素，同时有限元分析表明局压加载板的形状对局压承载力的影响较小.

4)通过参数分析提出圆钢管混凝土短柱局压极限承载力实用计算公式，计算结果与试验结果吻合较好.

[1] 蔡绍怀. 现代钢管混凝土结构[M]. 北京: 人民交通出版社, 2007:120-137.

CAI Shao-huai. Modern steel tube confined concrete structures[M]. Beijing: China Communications Press, 2007:120-137. (In Chinese)

[2] HAN Lin-hai, LIU Wei, YANG You-fu. Behavior of thin walled steel tube confined concrete stub columns subjected to axially local compression[J]. Thin-walled Structures, 2008, 46(2): 155-164.

[3] YANG You-fu, HAN Lin-hai. Concrete filled steel tube (CFST) columns subjected to concentrically partial compression [J]. Thin-walled Structures, 2012, 50(2): 147-156.

[4] 刘威, 韩林海. 钢管混凝土受轴向局压荷载时的工作机理研究[J]. 土木工程学报, 2006, 39(6):19-27.

LIU Wei, HAN Lin-hai. Behaviors of concrete-filled steel tubes subject axial local compression[J]. China Civil Engineering Journal, 2006, 39(6):19-27. (In Chinese)

[5] 丁发兴, 余志武. 钢管混凝土短柱力学性能研究-实用计算方法[J]. 工程力学, 2005, 22(3):134-138.

DING Fa-xing, YU Zhi-wu. A method for calculation of the mechanical properties of concrete-filled tubular steel stub columns[J]. Engineering Mechanics, 2005, 22(3):134- 138. (In Chinese)

[6] 霍静思, 何远明, 肖莉平,等. 高温后钢管混凝土抗多次冲击力学性能试验研究[J]. 湖南大学学报：自然科学版, 2012, 39(9):6-10.

HUO Jing-si, HE Yuan-ming, XIAO Li-ping,etal. Experimental study on the dynamic behavior of concrete-filled steel tube after exposure to high temperatures under multiple impact loading[J]. Journal of Hunan University: Natural Sciences, 2012, 39(9):6-10. (In Chinese)

[7] CECS28-2012 钢管混凝土结构技术规程[S]. 北京: 中国计划出版社, 2012:25-26.

CECS28-2012 Technical specification for concrete filled steel tubular structures[S]. Beijing: China Planning Press, 2012:25-26. (In Chinese)

[8] GB 50936-2014 钢管混凝土结构技术规范[S]. 北京: 中国建筑工业出版社, 2014:39-40.

GB 50936-2014 Technical code for concrete filled steel tubular structures[S]. Beijing: China Architecture & Building Press, 2014:39-40.(In Chinese)

[9] 谷利雄, 丁发兴, 付磊, 等. 圆端形钢管混凝土轴压短柱受力性能研究[J]. 中国公路学报, 2014, 27(1)：57-63.

GU Li-xiong, DING Fa-xing, FU Lei,etal. Mechanical behavior of concrete-filled round-ended steel tubular stub columns under axial load[J]． China Journal of Highway and Transport, 2014, 27(1):57-63. (In Chinese)

[10]DING Fa-xing, YING Xiao-yong, ZHOU Lin-chou,etal. Unified calculation method and its application in determining the uniaxial mechanical properties of concrete[J]. Front Archit Civ Eng China, 2011, 5(3): 381-393.

[11]Hibbitt, Karlson & Sorenson. Abaqus Version 6.4: Theory manual, users’ manual, verification manual and example problems manual[M]. Hibbitt, Karlson & Sorenson Inc, 2003.

Mechanical Behavior of Concrete-filled Steel Tubes Stub Columns with Circular Section under Local Compression

LIU Jing1, DING Fa-xing1, GONG Yong-zhi1†, YU Zhi-wu1,2，LI Da-wen1

(1.School of Civil Engineering, Central South Univ, Changsha,Hunan 410075，China; 2.National Engineering Laboratory for High Speed Railway Construction, Changsha,Hunan 410075,China)

This paper studied the mechanical properties of circular concrete-filled steel tubular (CFT) stub columns with local compression, conducted an experimental study of the local compression of 12 circular CFT stub columns and compared the influence of concrete strength grade and local compression area ratio on ultimate bearing capacity. It is found that the ultimate bearing capacity increases with the increase of concrete strength grade and the decrease of area ratio. Then, based on the reasonable material constitutive relation, it established a shell-solid 3D finite element model of circular CFT stub columns with local compression by using ABAQUS. And on the basis of the experiment verification, it explored the influence of local compression area ratio, steel ratio, and strength of steel and concrete on ultimate bearing capacity. Furthermore, this paper presented practical computational methods for the local compression bearing capacity of CFT stub columns with circular section by fitting analysis. It then compared the 47 groups of circular CFT stub columns, which combined the formula results, and calculation formula by other scholars, with the finite calculation results. The results show that the formula results are in good agreement with the experiment results.

concrete-filled steel tube; local compression; finite element method; ultimate bearing capacity

2014-12-11

国家科技支撑计划项目(2011BAJ09B02)；国家自然科学基金资助项目(51578548),National Natural Science Foundation of China(51578548)

刘 劲(1988-)，男，湖南安化人，中南大学博士研究生

†通讯联系人，E-mail:gyzh@yahoo.cn

1674-2974(2015)11-0033-08

TU398

A