简单子抽样多元双样本检验的改进方法

陈丽君， 朱永忠 ， 王方磊

(河海大学 理学院，江苏 南京211100)

近年来，非平衡类问题成为一个新的研究领域并应用于生物科学、金融、欺诈检测和文本挖掘等领域。这些领域中的数据分布是不均衡的，如信用卡使用中的欺诈行为通常少于正常使用行为。非平衡的多元双样本检验问题是非平衡数据研究的问题之一。随着现代计算机的广泛应用，检验方法的理论发展以及检验方法在其他学科中应用的增加，众多学者对双样本检验及其检验效力进行了大量研究。

早在1969 年，Bickel［1］在经典K-S 检验的基础上，利用混合样本的经验分布函数，建立了一种自由分布的多元Smirnov 检验。随后Friedman［2］于1979 年利用混合样本的最小生成树(MST)将最大偏离检验等双样本检验由一元情形推广到多元。1986 年Schilling［3］通过构造一种基于k-最近邻分类算法(KNN)的检验统计量来解决多元双样本检验问题，但是随着两样本不平衡度的增加，该方法的检验效力急剧减弱。2005 年Rosenbaum［4］提出一种基于观测点最小距离非二分图(MDP)的交叉匹配检验，该检验用于低维的大容量样本时表现出极高的检验效力。同年Aslan［5］用观测点在变量空间的距离作算术函数，构造了一种基于观测点间能量的多元检验统计量。后两种检验方法主要利用混合样本点之间的紧密性这一性质，而只有当两个样本的容量相当时，才能保证检验结果的有效性。同时，对这些检验方法一致性和渐近性的研究十分依赖于两样本平衡这一假设条件。针对这一问题，2013年CHEN Hao［6］考虑到在多元情形中，来自不同分布的样本点可能比来自同一分布的样本点有更密切的联系，从样本内部边缘的角度提高了相似图形检验方法的检验效力。而CHEN Lisa 等人［7］针对非平衡双样本检验效力下降的问题改进了Schilling的k 最近邻检验，提出一种简单子抽样的多元双样本检验方法(简称SSS-NN 检验)。SSS-NN 检验方法首先对大样本采用简单的随机子抽样，再进行Schilling 检验统计量的计算，但由于进行随机子抽样时丢弃了大样本的大部分数据，导致样本信息丢失而产生检验误差。

为此，文中研究基于SSS-NN 检验，从平衡样本容量和充分保留样本信息的角度出发，采用集成子抽样方法和加权调整方案，提高非平衡多元双样本检验的检验效力。

1 基于KNN 算法的简单子抽样多元双样本检验

KNN 算法(k-Nearest Neighbor)［8］是一种对局部性质非常敏感的惰性学习，在许多领域都有成功的应用，而且产生了各种各样的改进算法。KNN 算法的基本思路是:搜索模式空间找出距离最接近未知样本的k 个训练样本，未知样本被分配到k 个最近邻样本中占百分比最多的一类，其近邻性可以采用欧几里得距离、马哈拉诺比斯距离和曼哈顿距离等。

KNN 算法从混合样本集中搜索与未知样本最接近的k 个样本，对每个由j 个属性组成的样本，基于KNN 算法的SSS-NN 检验方法采用属性权值为1的欧几里得距离来度量样本点之间的近邻性:

假设点x ∈A，样本集A ⊂Rd，定义点x 在集合A{x}中的第k 个近邻样本点为NNk(x，A)。进行SSS-NN 检验时，对于相互排斥的集合A1和A2，首先使用如下示性函数来判断样本点x 与其所在集合(A1∪A2){x}上的第k 个近邻点是否来自同一样本:

假设Rd上的独立随机样本X = {X1，X2，…，Xn}，Y = {Y1，Y2，…，Y~n}分别服从未知分布F(x)和G(x)，且F(x)与G(x)在Lebesgue 空间上绝对连续。为了分析样本与总体之间的差异是否显著，提出检验的零假设为F(x)= G(x)。SSS-NN 检验的统计量

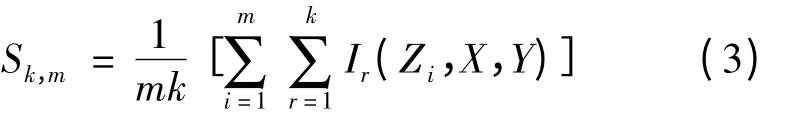
其中混合样本

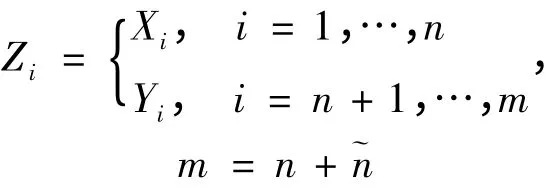
SSS-NN 检验的逐点统计量如式(4)，其衡量的是样本点Zi在集合X ∪Y 上的k 个最相邻的样本点中，与样本点Zi属于同一样本的点所占百分比。

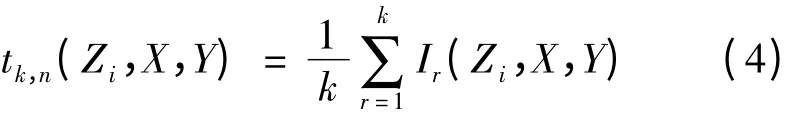
由文献［3］知，在H1下检验统计量Sk，m是连续的，即

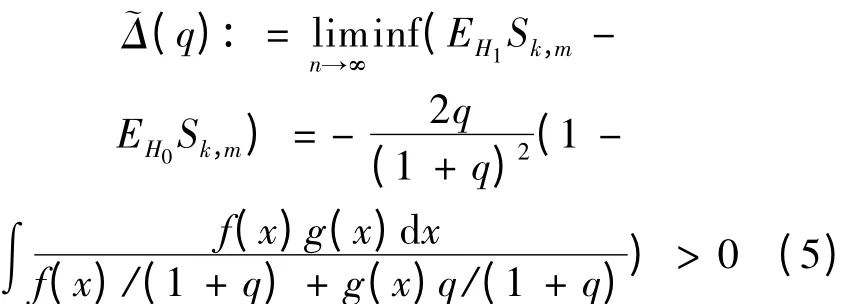
其中两样本容量比q = ~n/n 为样本非平衡度，f(x)，g(x)是分布F(x)，G(x)对应的密度函数。然而，当q 逐渐增大时，~Δ(q)的一致性非常弱，即当q →∞，~Δ(q)= o(1/q)。另外，若用以下效用系数¯η(q)表示Sk，m的渐近性，则当q →∞时，¯η(q)→0。因此当样本非平衡度趋于无穷时，Sk，m的渐近能力趋于零，也就是说，当样本非平衡度趋于无穷时，SSS-NN 方法的检验效力趋于零。

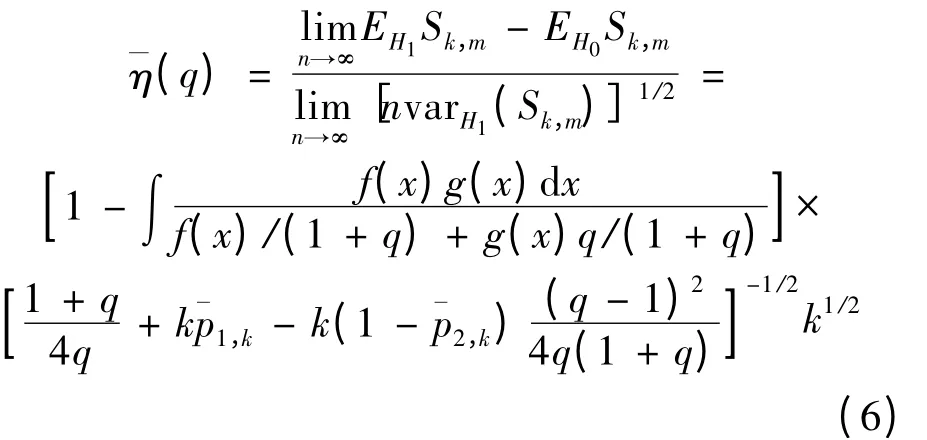
2 简单子抽样多元双样本检验的改进方法

2.1 集成子抽样方法

目前解决数据非均衡问题的方法大致分为两类［9］:数据水平方法和算法水平方法。均衡样本集可以考虑采用以下数据水平方法，一种是对大样本进行欠抽样，随机抽取一个样本容量与小样本容量相当的子集，另一种是对小样本实例进行过抽样。使用欠抽样方法和过抽样方法均可以减小两样本的非平衡程度。但这两种方法存在一些弊端，如欠抽样常常会丢失一些有用的多数类实例信息，过抽样则会增加许多重复的数据，并且这些数据不是独立同分布的，容易增大过分拟合的可能性。

近十余年来，集成方法［10］被广泛应用于回归问题和分类问题中。集成方法的核心思想是:对于一系列适合用于处理原始数据的简单模型，通过特定的算法或操作把它们组合成一个预测稳定性和准确度更高的新模型。集成子抽样方法贯彻这一思想，通过组合应用在不同混合样本的最近邻计算过程，从数据水平层面减小样本非平衡度，具体过程如下:对于每一个混合样本点Zi(i = 1，…，m)，若Zi∈X，则从大样本Y 中随机抽取一个容量为ns的子样本Si;若Zi∈Y，则从样本Y{Zi}中随机抽取一个容量为ns－1 的子样本Si，并将样本点Zi放入集合Si中，最后得到m 个容量为n + ns的混合样本X ∪Si。利用每一个混合样本点和相应的混合样本进行KNN 计算。

与仅对大样本进行一次简单子抽样的样本均衡方法相比，集成子抽样对混合样本的每一个点独立地从大样本中进行一次随机子抽样，充分保留了所有样本点的实例信息，同时事先对样本进行约简，能快速得出待判样本点是否属于同一样本。进行样本动态变化的KNN 计算，提高了逐点统计量的计算效率和准确性。

2.2 基于集成子抽样的改进SSS-NN 检验

当两个样本非平衡度很大时，即n ≪~n 时，随着样本非平衡度的增大，SSS-NN 检验方法的检验性能急剧减弱。这种现象同样存在于游程检验［11］和交叉检验［12］中，都是由大样本的主导性影响所引起的。简单地说，当大样本占混合样本的大多数时，无论在H0下还是在H1下，小样本X 上的被加数

较小，大样本Y 上的被加数

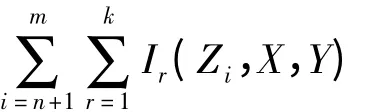
较大，增大了KNN 计算的误判率，从而导致SSS-NN方法在检验两个未知分布的差异时性能减弱。第1节的式(5)、式(6)从理论上解释了这一现象的本质。

文中提出集成子抽样方法从数据层面均衡两样本容量，以改善样本容量不平衡带来的问题。进行集成子抽样时，选择随机抽取容量为n 的子样本，为的是使检验的两个样本容量相当，从数据水平层面减小大样本的主导性影响。另一方面，当ns≠n时，还要考虑不同样本点共享同一近邻点这一问题，此时计算检验统计量的渐近方差十分困难。从而明智的选择是令ns= n。

文中在SSS-NN 检验的基础上，将集成子抽样与权重调整相结合提出改进的SSS-NN 检验——集成子抽样多元双样本检验(以下简称MESS-NN 检验)。具体步骤如下:

1)对问题提出检验假设，并预先选定显著性水平。通常情况下取α = 0.01 或0.05。

2)对待检验的两个样本进行集成子抽样。

3)进行集成子抽样后，采用基于欧几里得距离的k-最近邻算法进行逐点统计，即对每一个混合样本点Zi，计算与其属于同一样本的近邻样本点数量在混合样本X ∪Si中所占的比例:

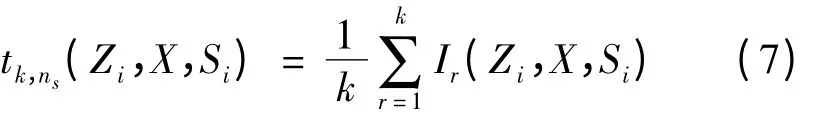
该步骤是对SSS-NN 检验的逐点统计过程的一次改进，每一个混合样本点进行最近邻计算的样本空间都是不同的。

4)计算检验统计量的样本观察值Tk，n。

利用m 个逐点统计量构造新的统计量时，权值的选择是一个很有意义的研究内容。由于进行逐点统计的混合样本点或者来自样本X，或者来自样本Y。上文提到过无论在零假设下还是备择假设下，最近邻计算的结果都受到大样本的主导性影响，因此使用权重分别调整两个待检验样本对检验结果的影响，确切地说，在使用逐点统计量构造检验统计量时，对属于样本的每一个混合样本点，通过赋予较小的权值调整相应统计量的权重，从而减小大样本的主导性对检验统计量的影响。根据样本非平衡度，选取点Zn+1，…，Zm的逐点统计量的权重为

综合上述集成子抽样方法和权值调整方案，提出一种受样本非平衡度影响较小的集成子抽样多元双样本检验统计量。于是，得到MESS-NN 检验统计量如下:

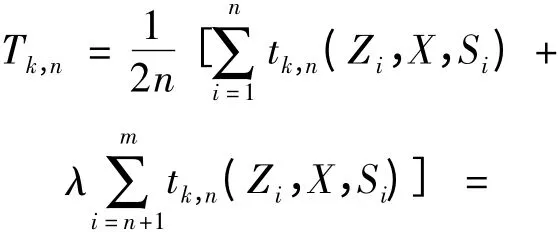
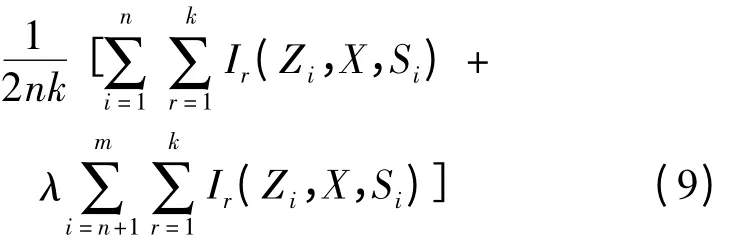
由于样本集X 与样本集Y 的检验是非对称的，因此要单独考虑下列情形:(1)样本集X 中的点互为近邻，即

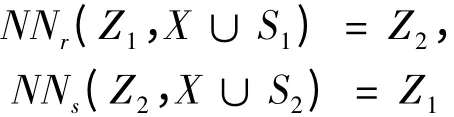
(2)样本集Y 中的点互为近邻，即

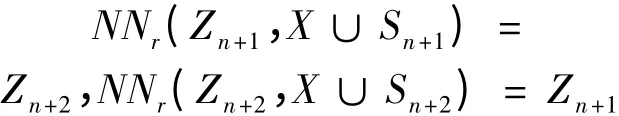
(3)样本集X 中的点与样本集Y 中的点有相同的近邻，即

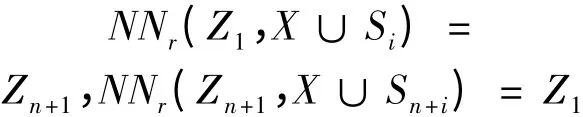
在H0下，MESS-NN 检验统计量的渐近零分布是以下正态分布:

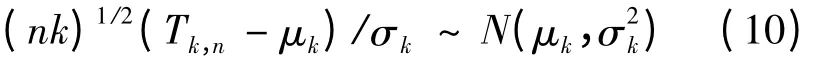
其中

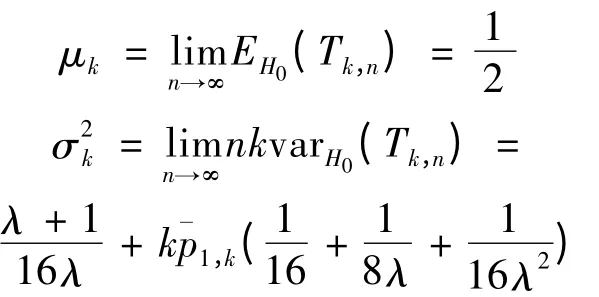
这里

5)重复步骤2 ～4 N 次，并对N 次统计量的计算结果取平均值，一般来说，重复的次数越多，检验结果越准确。

6)根据所提出的显著水平，确定临界值和拒绝域，并做出检验决策。

3 仿真实验与实证分析

3.1 仿真实验

在假设同一样本数据服从以下6 组随机选取的正态分布模型的前提下，用Monte-Carlo 方法分别生成1维和5 维的随机样本进行仿真实验，运用SSS-NN 方法和MESS-NN 方法对随机样本进行双样本检验，利用Matlab 软件编程并绘制相应的检验效力图。

1)方差相同的正态分布。每一个模型随机选取两个样本方差相同而样本均值不同的正态分布。两组分布的参数分别为

模型1.1

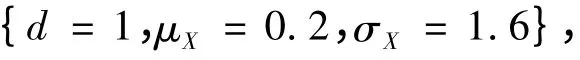
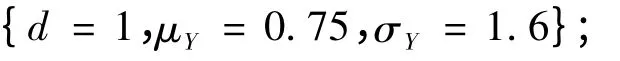
模型1.2

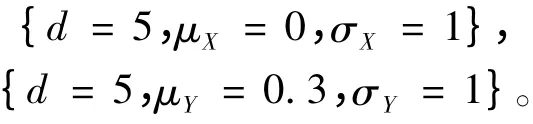
2)均值相同的正态分布。每个模型的两个分布都有相同的样本均值向量μLd，不同的样本协方差矩阵σ2Id，其中Ld为d 维单位向量，Id为d 阶单位阵。分布的参数分别为

模型2.1

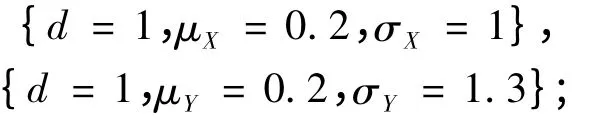
模型2.2

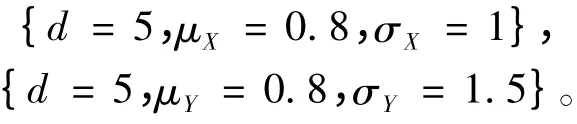
3)方差、均值都不相同的正态分布。每个模型的两个分布的样本均值向量μLd和样本协方差矩阵σ2Id均不同。分布的参数分别为

模型3.1

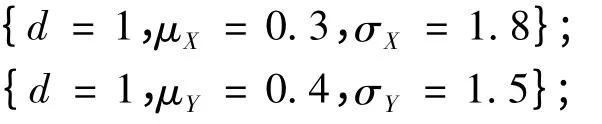
模型3.2

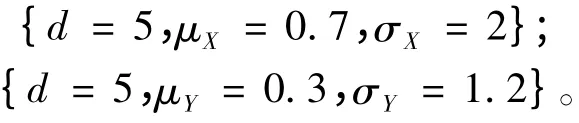
使用SSS-NN 方法或MESS-NN 方法进行400 次双样本检验，用拒绝H0的次数占检验总次数的百分率来衡量检验效力。在实验中分别选择1 维和5 维的正态分布数据作为实验对象，对于每一个1 维或5维的正态分布模型，均从第1 个正态分布中随机抽取一个容量为100 的小样本，再从第2 个正态分布中随机抽取容量分别为100，400，1 600，6 400 的大样本;在显著性水平α = 0.05 下使用SSS-NN、MESS-NN 方法进行检验，并做出检验决策，最后计算检验效力。以KNN 计算过程中k 的取值为横坐标，以检验效力为纵坐标，得到样本非平衡度为q =1，4，16，64 时的检验效力如图1，2 所示。由于每个模型中的两个正态分布均不相同，因此越是检验效力强的检验方法，越应该以大概率拒绝H0。

图1(a)和图2(a)分别展示SSS-NN、MESS-NN方法应用于随机模型1.1 的检验效力，图1(b)和图2(b)是模型2.1 的检验结果，图1(c)和图2(c)是模型3.1 的检验结果等。观察图1(a)～1(f)可知，当小样本容量固定时，随着非平衡度q 的增大，SSS-NN 方法的检验效力急剧减弱，在多元情形下，样本比为16 或64 时检验效力不高于20%，甚至无法检验两个样本之间的差异，如图1(b)、图1(e)、图(f)所示。相比之下，观察图2(a)～2(f)可知，MESS-NN 受比值q 的影响较小，样本不平衡下检验效力甚至高达80%，说明MESS-NN 方法在检验非平衡的多元双样本问题时比SSS-NN 方法更优越。

3.2 实例分析

收集、整理了淮河流域2007 年1 月至2011 年12月和白水河流域2010 年1 月至2011 年12 月的历史测量数据，对于个别缺测的气象数据，利用邻近站点资料进行相关插补。随后分别使用SSS-NN 检验和MESS-NN 检验分析这两个流域在逐日平均流量、逐日降水量、逐日水面蒸发量这3 个方面是否存在显著差异。

数据预处理首先采用算术平均法将流域内的各站点降水转换成面平均降水，其中原始数据有淮河流域的大坡岭站、黄冈站等13 个气象站点，白水河有七邻站、叶氏祠站等12 个气象站点。处理得到的逐日降水量与对应日期的逐日平均流量、逐日水面蒸发量构成1 个三维向量，得到淮河流域1 825 个样本点，白水河流域730 个样本点，样本容量比q =2.5。将SSS-NN 方法和MESS-NN 方法应用于这两个样本，取显著性水平α = 0.05，所得检验效力比较结果如表1 所示。

图1 SSS-NN 方法在q = 1，4，16，64 时的检验效力实验结果Fig.1 Simulation results comparing the power of the SSS-NN for q = 1，4，16，64

图2 MESS-NN 方法在q = 1，4，16，64 时的检验效力实验结果Fig.2 Simulation results comparing the power of the MESS-NN for q = 1，4，16，64

表1 原始SSS-NN 方法和改进SSS-NN 方法的检验效力结果比较Tab.1 Power value for comparing the original SSS-NN and the improved SSS-NN method

由表1 可知z ＞zα/2，即统计量的值落在了拒绝域，因此拒绝H0，认为这两个样本存在显著差异。图3(a)、图3(b)分别是两个流域样本的平均水面蒸发量分布图，特别地，图3(b)相对于图3(a)而言呈现“长尾”状，显然淮河流域样本和白水河流域样本存在显著差异。因此对于SSS-NN 检验方法而言，MESS-NN 检验方法能以更高的检验效力体现出这两个样本的显著差异。

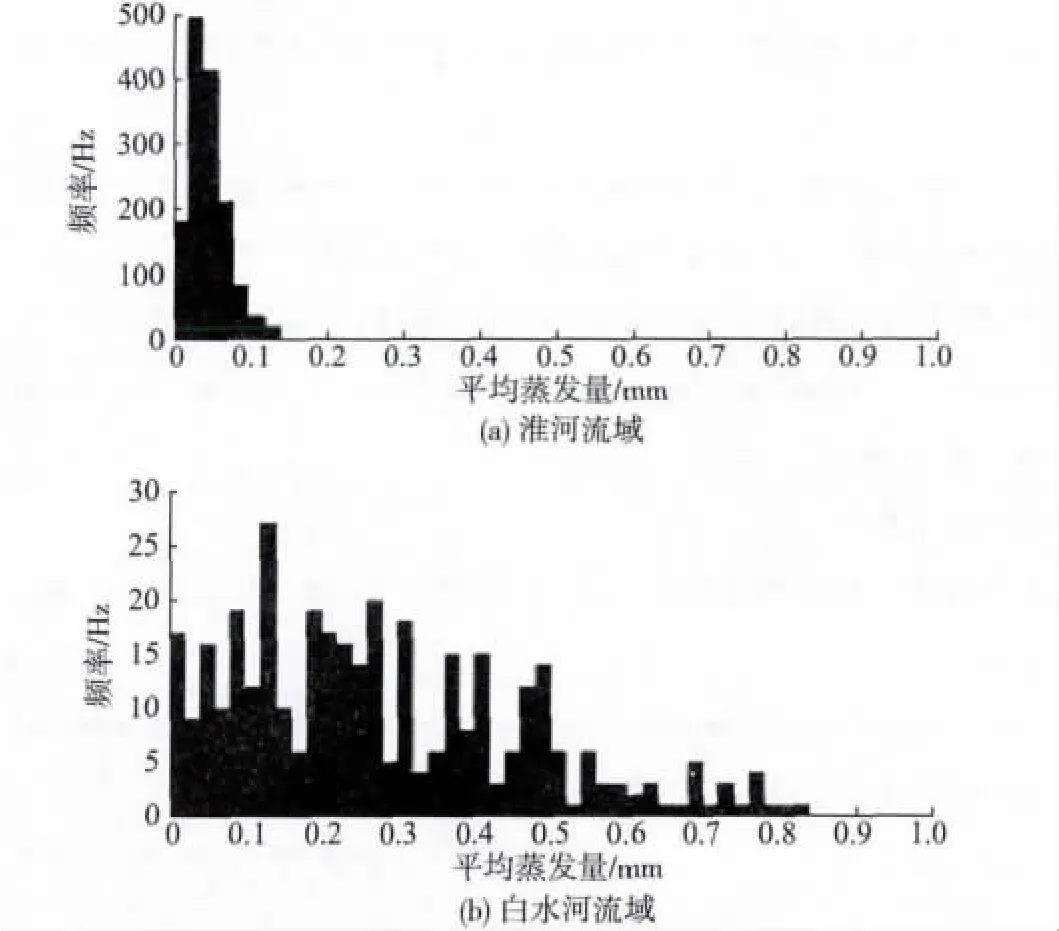
图3 淮河流域、白水河流域平均水面蒸发量分布Fig.3 Histograms of Huaihe River and Baihe River in precipitation

事实上由于河流的平均流量、降水量、水面蒸发量受地理位置、地形、气候、植被、水利调控等因素的影响［13-15］，所以该检验结果符合实际情况，是合理的。

4 结 语

为了解决非平衡多元双样本的检验问题，将集成子抽样方法应用于基于KNN 算法的简单子抽样多元双样本检验中，由于进行集成子抽样，极大地保留了样本数据的信息，因此有效地达到了平衡样本容量的目的。同时由于构造检验统计量时采用了加权运算，减弱了大样本对KNN 计算结果带来的主导性影响，提高了检验效力。最后，多次重复检验，减小了混合样本随机性带来的影响，进一步提高了检验结果的准确率。仿真实验表明，集成子抽样多元双样本检验有效地改善了简单子抽样多元双样本检验在检验非平衡多元双样本时检验效力下降的问题。

改进后的简单子抽样多元双样本检验还有很多局限，如KNN 算法的计算时间过长。另外，对于两个样本容量都较小且样本非平衡的情形，过少的观测点导致MESS-NN 方法的检验效果不理想，因此寻找适用于这种情形的检验方法也是一个值得研究的方向。

［1］Bickel P J. A distribution free version of the Smirnov two sample test in the p-variate case［J］. The Annals of Mathematical Statistics，1969，40(1):1-23.

［2］Friedman J H，Rafsky L C. Multivariate generalizations of the wald wolfowitz and smirnov two-sample tests［J］. The Annals of Statistics，1979，7(4):697-717.

［3］Schilling M F. Multivariate two-sample tests based on nearest neighbors［J］. Journal of the American Statistical Association，1986，81(395):799-806.

［4］Rosenbaum P R.An exact distribution-free test comparing two multivariate distributions based on adjacency［J］. Journal of the Royal Statistical Society:Series B:Statistical Methodology，2005，67(4):515-530.

［5］Aslan B，Zech G. New test for the multivariate two-sample problem based on the concept of minimum energy［J］. Journal of Statistical Computation and Simulation，2005，75(2):109-119.

［6］CHEN H，Friedman J H. New graph-based two-sample tests for multivariate distributions［BE/OL］.2013-07-15. http://arxiv.org/abs/1307.629.

［7］CHEN L，DOU W W，QIAO Z.Ensemble subsampling for imbalanced multivariate two-sample tests［J］.Journal of the American Statistical Association，2013，108(504):1308-1323.

［8］王永吉，杨慧中.基于K-近邻的支持向量机多模型建模［J］.江南大学学报:自然科学版，2010，9(1):7-10.

WANG Yongji，YANG Huizhong，Compositional support vector machine model based on improved k-kearest neighbor algorithm［J］.Journal of Jiangnan University:Natural Science Edition，2010，9(1):7-10.(in Chinese)

［9］孙晓燕，张化祥，计华.用于不均衡数据集分类的KNN 算法［J］.计算机工程与应用，2011，47(28):143-145.

SUN Xiaoyan，ZHANG Huaxiang，JI Hua. Improved KNN algorithm in classification of imbalanced data set［J］. Computer Engineering and Applications，2011，47(28):143-145.(in Chinese)

［10］石静，邱立坤，王菲，等.相似词获取的集成方法［C］//孙茂松，陈群秀. 中国计算语言学研究前沿进展(2009-2011)，北京:清华大学出版社，2011:277-283.

［11］滕云龙，师奕兵.GPS 载波相位测量数据的时间序列分析建模研究［J］.电子测量与仪器学报，2009，29(9):18-22.

TENG Yunlong，SHI Yibing.Study on modeling of time series analysis for GPS carrier phase measurement data［J］. Journal of Electronic Measurement and Instrument，2009，23(9):18-22.(in Chinese)

［12］张毅，刘毅坚，罗元.一种基于参数优化C-SVM 的脑电信号分类方法及应用［J］.重庆邮电大学学报:自然科学版，2014，26(1):131-136.

ZHANG Yi，LIU Yijian，LUO Yuan. A parameter optimized C-SVM approach for EEG classification and its application［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition，2014，26(1):131-136.(in Chinese)

［13］王国庆，张建云，刘九夫，等.中国不同气候区河川径流对气候变化的敏感性［J］.水科学进展，2011，22(3):307-314.

WANG Guoqing，ZHANG Jianyun，LIU Jiutian，et al. The sensitivity of runoff to climate change in different climatic regions in China［J］.Advances in Water Science，2011，22(3):307-314.(in Chinese)

［14］袁飞.考虑植被影响的水文过程模拟研究［D］.南京:河海大学，2006.

［15］曹宇峰，刘高峰，王慧敏.基于Mann-Kendall 方法的淮河流域降雨量趋势特征研究［J］.安徽师范大学学报:自然科学版，2014，37(5):477-480.

CAO Yufeng，LIU Gaofeng，WANG Huimin. Huaihe river basin rainfall trend characteristics research based on Mann-Kendall method［J］.Journal of Anhui Normal University:Natural Science，2014，37(5):477-480.(in Chinese)