双塔结构架空连体舒适度分析

宋秋璐， 朱召泉 ， 李 华

(1.河海大学土木与交通学院，江苏南京210098;2.中交第四航务工程勘察设计院有限公司，广东广州510220)

近年来，连廊结构随着多高层建筑的快速发展大量出现。在各种商业建筑、体育建筑、交通建筑中常常可以看到连廊结构。这些大跨度连廊结构，竖向自振频率较低，人行荷载可能会引起结构竖向振动及共振响应，引起舒适度问题，因此对连廊结构进行舒适度分析很有必要。

为了防止结构振动过大，国内规范［1］采取对结构基频进行控制，避开人的步行频率共振频段，从而控制加速度响应。目前国内针对结构舒适度的计算方法主要分为两类:一是采用简化的近似方法［2］;二是采用有限元计算方法［3］，即建立结构的有限元模型，在其上施加各工况下的人行荷载，计算结构的加速度响应，并根据计算结果及预先选定的舒适度评价标准，来评价结构的舒适度性能。

国外对结构舒适度做了不少研究。学者通过对大量试验数据统计分析，统计出人行走的步频平均值为1.9 Hz，标准差为0.2 Hz。假定人走路时左右脚产生的单步落足曲线相同，基于此，先后提出模拟人走动过程激励力时程曲线的构造方法。Allen和Rainer［4］对单人连续行走产生的动力荷载进行研究，认为人行走的激励力可以通过取傅里叶级数前几阶，采用一系列简谐波组合来模拟。简谐波随着频率的加倍在总激励力中所占比重逐渐减小，其比重用一个动载因子αn来表示，前4 个简谐波组成了动力荷载的大部分。

在傅里叶级数模型里，第一阶简谐波组成了动力荷载的大部分，在实际应用中往往只考虑第一个简谐波影响，而忽略高阶简谐波影响。《美国钢结构设计指导11-人的活动引起的楼板振动》［5-6］即采用了该荷载简化模型，称为人连续行走曲线的正弦函数模型。

文中参考人行桥结构的舒适度评价标准对钢连廊结构进行舒适度分析。

1 人行荷载模型及舒适度评价标准

1.1 人行荷载模型

人行荷载模型(International Association for Bridge and Structural Engineering，IABSE)［7］如图1所示，它提供的连续步行荷载公式如下:

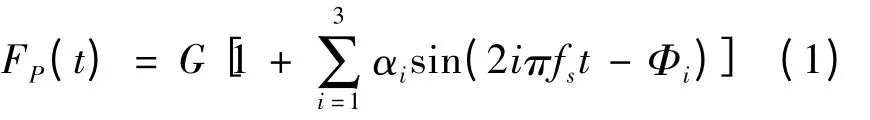
式中:FP为行人激励荷载，单位N;G 为人体质量，单位N;αi为第阶荷载频率的动力系数;fs为第阶荷载频率，单位Hz;t 为时间，单位s;Φi为第阶荷载频率的相位角。

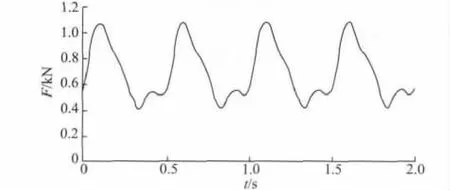
图1 连续行走荷载模型曲线Fig.1 Curve of the continuous walking load’s model

根据文献［8］对舒适度计算公式的推导，公式(1)可以简化为

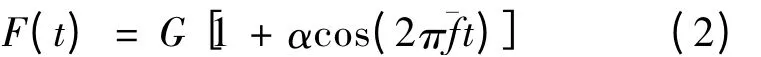
式中，α 为对应荷载频率¯f 的动力系数。动力系数α和荷载频率¯f 的关系式近似用下式表示:

1.2 人行桥结构舒适度评价标准

对于文中研究的钢结构人行天桥连廊，根据其使用和结构特点并参考文献［9］，提到各国规范或设计标准规定了加速度允许值，但国内尚无统一的舒适度评价指标。各国规范和设计标准中有很多类似指标，如Diekmann 指标、欧洲ECCS 规范指标、ISO10137 规范指标和我国列车车体加速度指标。其中以英国BSI［10-11］提出的舒适度评价方法最为简单易行，BSI 规定的舒适度最大加速度允许值可以表达为

式中，fv为结构自振频率。

文献［12］采用峰值加速度作为评价指标较为简单;结构竖向振动舒适度评价标准采用美国规范AISC—11 中推荐的室外人行天桥峰值按竖向振动加速度限值0.05 g，即0.5 m/s2。

2 钢连廊振动特性分析

工程概况:某双塔楼钢结构连廊结构体系:塔楼高34 m，共9 层，除底层层高6 m，其余层高皆为4 m。塔楼之间设置钢结构连廊，连廊跨度为24.8 m，宽3 m，连廊桥面支承纵向主梁采用H 型钢，截面(mm)形式为H1 000 ×400 × 28 × 32，水平横梁采用截面(mm)形式为H300 ×200 ×10 ×12，连廊楼面板采用压型钢板组合楼板，板厚150 mm，钢连廊结构如图2 所示。

2.1 结构计算模型

根据结构实际情况，考虑实际的约束条件，采用有限元软件ANSYS10.0 进行建模，塔楼梁、柱及钢连廊杆件采用beam188 单元模拟，楼板采用壳单元shell63 模拟;使用的基本单位为N，m，kg。模型如图3 所示。

2.2 动力特性分析

结构的固有频率和振型是承受动态荷载结构设计的重要参数，也是其他动力分析问题的起点。按照人行桥动力性能的评价指标，依据《城市人行天桥与人行地道技术规范CJJ69 —95》给出的舒适度标准，即竖向振动自振频率不小于3 Hz。

运用有限元软件Ansys 进行整体结构模态分析，默认采用Block Lanczos(分块兰索斯)法。

由于结构的模态分析主要受结构的质量与刚度影响，因钢结构连廊与其连接的钢筋混凝土结构塔楼，二者的材料不一样，在采用ANSYS 分析时，以命令流的形式赋予结构各自的弹模、密度DENS，Ansys 软件会根据各构件的尺寸自行计算结构各部分的刚度和质量。

图2 钢连廊平面布置Fig.2 Plan layout of the steel corridor floor

图3 双塔楼钢连廊结构有限元模型Fig.3 Finite element model graph of the steel connecting corridor structure of the twin-tower

初步分析表明，单独对连廊建模进行模态分析，比按结构整体建模进行模态分析得到的自振频率高，更易于满足规范要求的钢连廊舒适度(自振频率不小于3 Hz)。考虑到整体分析模型对连廊的影响，下面用Ansys 瞬态分析研究连廊舒适度时采用整体建模方式进行研究。分析结果如表1 ～2所示。

连廊与塔楼刚接时计算所得最低竖向自振频率为4.93(第9 阶振型)，铰接时的最低竖向自振频率3.33。计算结果表明，该双塔楼钢结构连廊体系的舒适度满足规范要求。

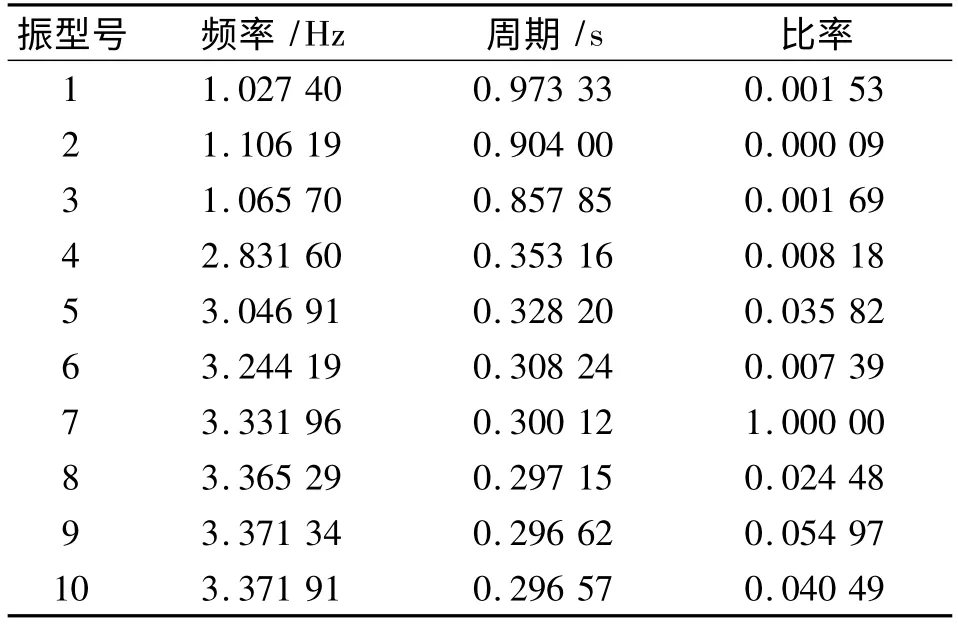
表1 铰接竖直(Z)方向模态参与因子计算Tab.1 Calculation of the modal participation factor in vertical direction of hinge

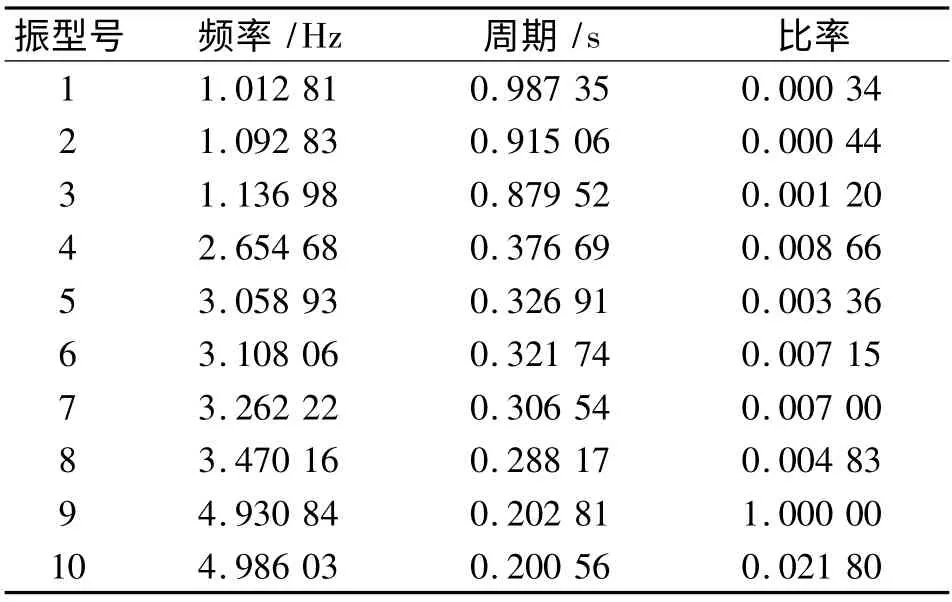
表2 刚接竖直(Z)方向模态参与因子计算Tab.2 Calculation of the modal participation factor in vertical direction of rigid connection

2.3 人行激励的加载与计算

人行激励是一种非常复杂的连续激励，具有较大的随意性。人在行走过程中不仅会有不同的体重，不同的行走方向，也会有不同的步频、步幅和双足落地的时间差，以及在结构上不同的行走位置，这些因素都使得人行激励成为非常复杂的问题。

为了模拟人行荷载对建筑结构的振动影响，通过分析做如下假定:

1)取单个行人的体重平均值为70 kg;

2)人的行走方向不予考虑;

3)人行进过程中激励形式保持不变。

人行走的各类动力指标如表3 所示［12］。

由公式(3)可求得动力系数α，由第1 阶钢结构阻尼比为0.02 和表2 数据，可根据公式(2)求得荷载余弦函数，建立6 组工况比较分析(见表4)。

通过Ansys 瞬态分析，把人步行荷载模拟为余弦荷载。本例模拟人群同时从连廊一端往跨中步行，得到几组工况的最不利点(跨中控制点)的加速度-时间曲线如图4 ～9 所示。

表3 人行走的各类动力指标Tab.3 List of all types of dynamic indexes of walking people

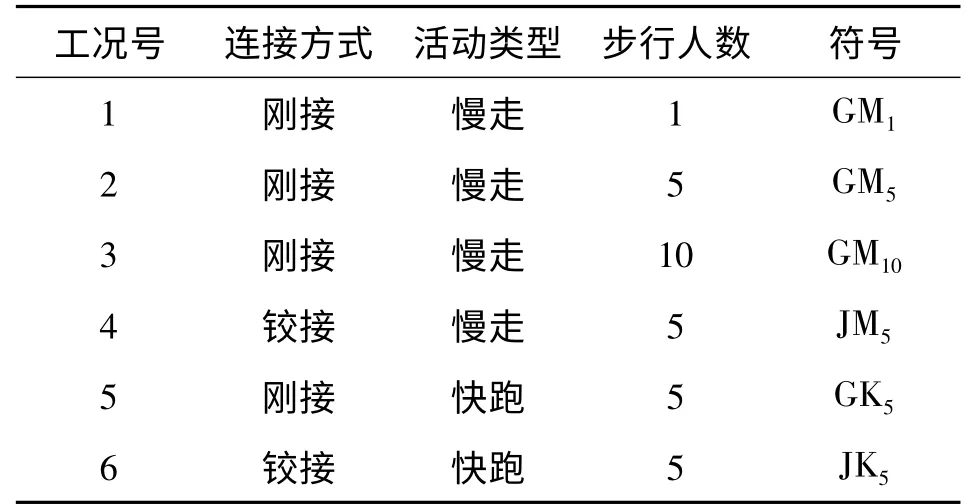
表4 人行走廊的计算工况Tab.4 Several sets of cases of the pedestrian corridor

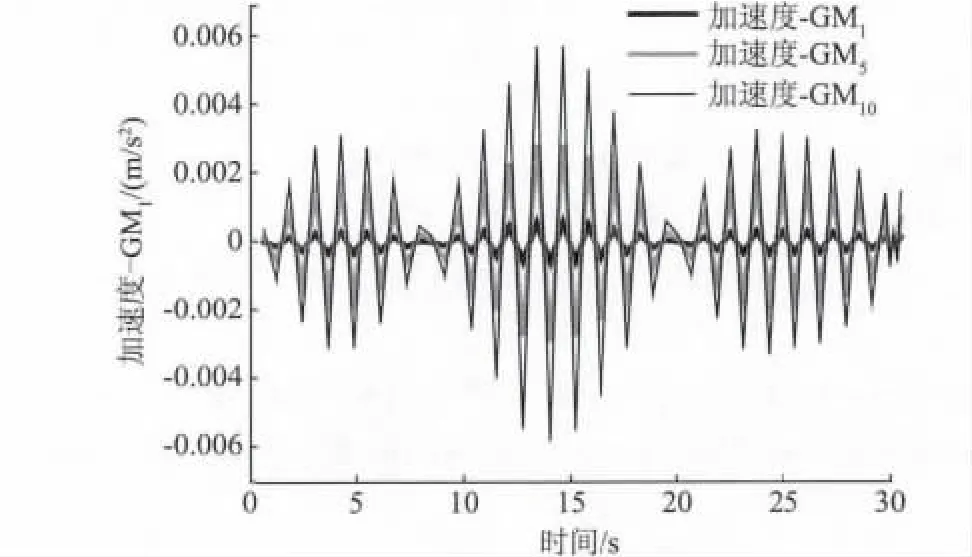
图4 工况1 ～3 跨中控制点加速度时程曲线Fig.4 Acceleration as functions of time of the controlled points in the middle of the span at case1，case2，case3

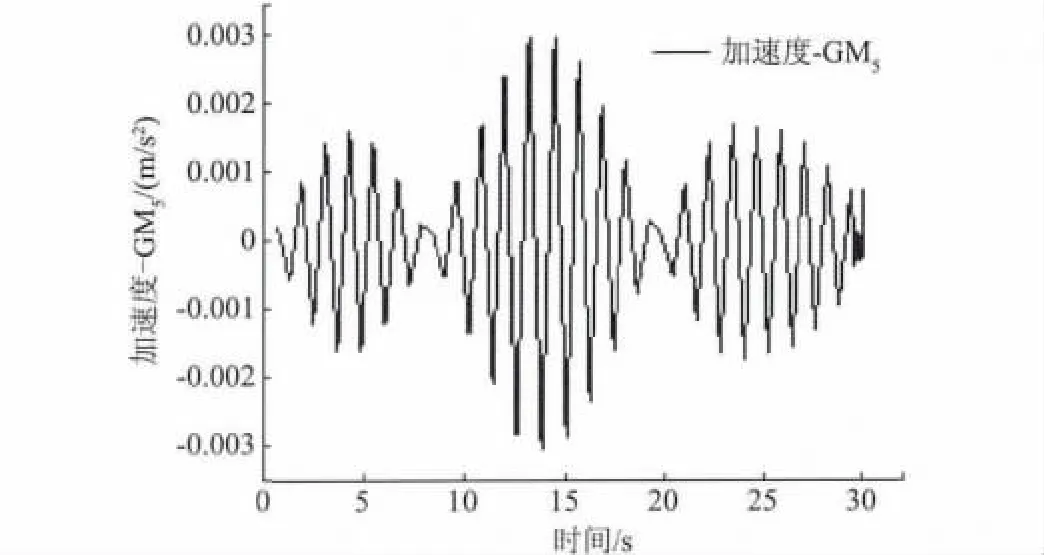
图5 工况2(GM5)跨中控制点加速度时程曲线Fig.5 Acceleration as functions of time of the controlled points in the middle of the span on the working conditions of group 2(GM5)

图6 工况2，4(GM5、JM5)跨中加速度时程曲线Fig.6 Acceleration as functions of time of the controlled points in the middle of the span at case2(GM5)and case4(JM5)

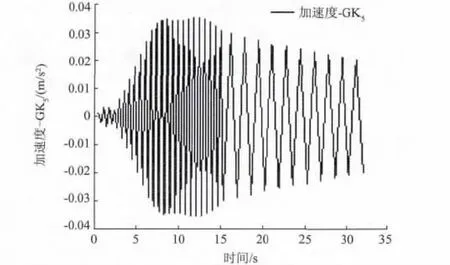
图7 工况5(GK5)跨中控制点加速度时程曲线Fig.7 Acceleration as functions of time of the controlled points in the middle of the span at case5(GK5)

图8 工况6(JK5)跨中控制点加速度时程曲线Fig.8 Acceleration as functions of time of the controlled points in the middle of the span at case6(JK5)

图9 工况5，6 跨中控制点加速度时程曲线Fig.9 Acceleration as functions of time of the controlled points in the middle of the span at case5(GK5)and case6(JK5)

峰值加速度都小于0.5 m/s2，满足要求;再由公式(4)得amax≤0.5= 0.5 ×≈0.5 m/s2，也满足要求。由图4 可以看出，步行人数越多，峰值加速度越大，说明峰值加速度与步行荷载大小有关。从图6 可以看出，其他条件相同，连廊与塔楼铰接连接比刚接连接峰值加速度大，说明峰值加速度与连廊与塔楼连接形式有关。对比图5 和图7，快跑比慢走大，说明峰值加速度与脚步频率有关。从图9 可以看出(对比图7 和图8)，快跑时刚接反而比铰接大，说明脚步频率越接近连廊自振频率，峰值加速度越大。

3 结 语

采用ANSYS 软件对几组连廊型式进行分析模拟，得出以下结论:

1)连廊结构竖向振动基本频率大于3 Hz，满足规范规定的舒适度要求;

2)人行激励下，钢连廊与塔楼在刚接、铰接情况下，竖向峰值加速度均满足舒适度要求，为简化安装，建议采用铰接连接;

3)峰值加速度的大小与步行荷载大小、步行频率、连接形式，以及步行频率和连廊自振频率有关;

4)人引起楼板振动的激励源和楼板舒适度具有较大模糊性，只能进行控制计算。

［1］北京市市政工程研究院.CJJ69—95 城市人行天桥与人行地道技术规范［S］.北京:中国建筑工业出版社，1996.

［2］中国建筑工业出版社.JGJ3—2010 高层建筑混凝土结构技术规程［S］.北京:中国建筑工业出版社，2011.

［3］朱鸣，张志强，柯长华，等.大跨度钢结构楼盖竖向振动舒适度的研究［J］.建筑结构，2008，38(1):72-76.

ZHU Ming，ZHANG Zhiqiang，KE Changhua. Study on improving people’s comfortableness on large-span steel floor structures［J］.Building Structure，2008，38(1):72-76.(in Chinese)

［4］Allen D E，Murray T M.Design criterion for vibrations due to walking［J］.Engineering Journal，1993，30(4):117-129.

［5］AISC.Steel design guide series No.11，floor vibrations due to human activities［S］. Chicago，Illinois:America Institute of Steel Construction，1997.

［6］吴超.某工程楼板人行振动舒适度研究［D］.天津:天津大学，2012.

［7］陈刚，周杰.人行激励下大跨度钢结构连廊舒适度分析［J］.安徽理工大学学报:自然科学版，2013，33(4):

CHEN Gang，ZHOU Jie.Comfort analysis of long-span steel corridor stimulated by pedestrian［J］.Journal of Anhui University of Science and Technology:Natural Science，2013，33(4).(in Chinese)

［8］娄宇，吕佐超，黄健.人行走引起的楼板振动舒适度设计［J］.特种结构，2011，28(2):1-4.

LOU Yu，LV Zuochao，HUANG Jian，The design of floor＇s vibration serviceability caused by the loads when people walk［J］.Special Structures，2011，28(2):1-4.(in Chinese)

［9］安日新，李毅，王杨，等.某大跨度钢连桥减振及舒适度分析［J］.中国建筑科学研究院.第二十三届全国高层建筑结构学术会议论文，北京:中国建筑科学研究院，2014.

［10］The Govemment of the Hong Kong Special Administrative Region.The Code of Practice for the Structural Use of Steel［S］.Hong Kong:The Government of the Hong Kong Special Administrative Region，2005.

［11］Bachmann H.Lively footbridges-a real challenge［C］//Footbridge 2002 Conference.Paris:［s.n.］，2002.

［12］黄健，王庆扬，娄宇.基于国内外不同标准的人行天桥舒适度设计研究［J］.建筑结构，2008，38(3):106-110.

HUANG Jian，WANG Qingyang，LOU Yu. Comfortable degree design for footbridges based on the criterions of domestic and overseas［J］.Building Structure，2008，38(3):106-110.(in Chinese)