基于EEMD 和PCA 滚动轴承性能退化指标的提取方法
肖顺根, 马善红, 宋萌萌, 孔庆光
(1.宁德师范学院 物理与电气工程系,福建 宁德352100;2. 浙江理工大学 机械与自动控制学院,浙江杭州310018)
滚动轴承是旋转机械中应用最为广泛的零部件之一,具有承受载荷的作用和相对运动的功能,其运行状态直接关系到设备整机性能及寿命[1]。为了避免灾难性事故的发生,有效地实施状态基维修,越来越迫切需要了解滚动轴承运转过程中各阶段的健康状态即运行过程中的衰退状况[2]。为此,如何提取从开始运行直至失效全过程的滚动轴承性能退化指标尤为重要。目前,表征性能退化指标的特征域有时域、频域和时频域3 种。其中,时域和频域因计算简单且不涉及参数选取问题,从而应用较广泛。徐小力等[3]利用振动烈度等时域指标对大型旋转机械设备的运行状态进行跟踪。Shichang等[4]通过提取时域和频域共17 个特征域信息作为滚动轴承寿命预测模型的输入向量,并获得了较好的剩余寿命预测效果。
近年来,随着小波分析、经验模态分解(Empirical Mode Decomposition,EMD)等非线性信号处理方法的出现,时频域特征指标也被广泛采用。文献[5-7]利用小波包变换方法或EMD 技术提取各频带能量及其总能量来组成时频域特征向量,较好地实现滚动轴承的性能退化评估。上述研究成果在某种程度上确实为滚动轴承的性能退化趋势预测取得了一定效果,但是,这些成果的性能退化指标基本上是基于某一种特征域建立。实际上,滚动轴承的运行状况是复杂的,仅依靠时域、频域或时频域中某一种特征域的退化指标分析其健康状况往往是不够全面的。
基于此,文中在文献[8]的基础上,通过对轴承全寿命振动信号进行集成经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)运算,得到一组本征模态函数(Intrinsic Mode Function,IMF)分量,利用相关系数准则对本征模态函数分量进行筛选并重构。对重构信号分别提取时域、频域和时频域3 种特征向量,利用主成分分析(Principal Component Analysis,PCA)法加权融合这3 个特征域,从而构建能够全面表征滚动轴承全寿命过程的性能退化指标。
1 EEMD 原理
1.1 EEMD 算法
WU[9]等提出的EEMD 是EMD 的一种改进算法,能够克服EMD 算法产生非白噪声干扰所引起的模态混叠现象。其思想是利用白噪声的频谱均匀性,将噪声数据随机分布到合适的时间点上,有效地抑制了信号奇异点的影响,又利用白噪声的零均值性能,经过多次平均运算后有效地抵消了噪声的影响,其本质是一种叠加高斯白噪声的多次经验模式分解[10]。
EEMD 算法分解步骤[11]如下:
1)给初始信号x(t)分别加入N 次均值为零,幅值标准差为常数的高斯白噪声ωi(t),构建一个总体信号xi(t),即
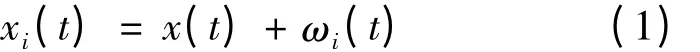
式中,ωi(t)的强度取决于高斯白噪声标准差与初始信号标准差之比Rstd,i = 1 ~N。
2)对各个信号xi(t)分别进行EMD 分解,获得l 个本征模态函数IMF 分量及1 个残余项ri(t):
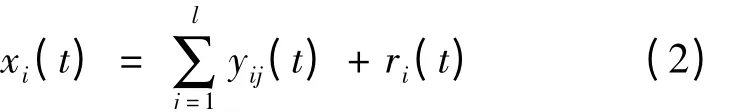
式中,yij(t)是第i 次加入高斯白噪声ωi(t)经EMD分解后得到的第j 个IMF 分量。
3)对所有的IMF 分量yij(t)进行均值运算,消除多次加入ωi(t)对真正的IMF 影响,最终得到了IMF 分量yj(t)和残余项r(t),如式(3)与式(4)所示。

式中,yj(t)为EEMD 对信号x(t)分解后得到的第j个IMF 分量。因此,被EEMD 分解的信号x(t)可由l个yj(t)和1 个r(t)构成,如式(5)所示。

1.2 有效IMF 分量提取
初始信号经EEMD 分解后,由于分解误差和插值误差等多重因素,使分解结果中IMF 分量易产生虚假分量。如果虚假分量存在特征域中,显然会使提取的退化性能指标产生较大误差。因此,将虚假分量剔除掉是十分必要的。考虑虚假分量与初始信号的关联性较小,因此可通过引入相关系数来辨别虚假分量。相关系数的数学表达式如下:

式中,λj(j = 1,…l)为所有IMF 分量与原始信号的相关系数,x 和¯x 分别表示为初始信号及其平均值,y和¯y 分别表示为IMF 分量信号及其平均值,n 为振动信号采集数据样本点数。
随后,设置辨别虚假分量阈值μ 值,若IMF 分量与初始信号的相关系数小于μ 值则将其剔除,最终将大于μ 值的IMF 分量保留下来并重构,从而获得有效的初始信号,达到降噪目的。
2 提取多特征域信息
采集的全寿命滚动轴承振动信号信息非常庞大,不利于数据分析。为此,非常有必要对采集的数据进行特征提取处理,以简化后续数据分析工作量。另外,采集的振动信息仅是一维的时域信息,而轴承的运行状况包含了轴承的多种形式,多种特征集合,多种状况征兆信息,若仅用一维的时域信息很难全面表征滚动轴承运行特征,亟需从时域、频域和时频域3 种特征域来获取轴承的全面信息。
2.1 时域特征提取
时域特征指标包括有量纲和无量纲。在反映滚动轴承性能退化趋势上,有16 种时域特征指标均能较好地表征,其中有量纲包含均值、方差、最大值、最小值、方根幅值、绝对平均幅值、歪度、峭度、均方根和峰峰值10 种,无量纲包含波形指标、峰值指标、脉冲指标、裕度指标、峭度指标和偏斜度指标6 种。关于16 种时域特征指标的数学表达式详见相关文献[8]。
2.2 频域特征提取
滚动轴承性能退化频域特征指标主要选择与频谱相关的信息,如故障位置的频率及相应的幅值等。常提取的频域特征指标反映频域振动能量大小、频谱的分散或者集中程度和主频带位置的变化3 种特征,各指标的数学表达式如式(7)至式(19)所示。其中p1(均值频率)反映频域振动能量大小,p2(标准差)、p3(特征1)、p4(特征2)、p6(特征3)、p10(特征6)、p11(特征7)、p12(特征8)、p13(特征9)反映频谱的分散或者集中程度,p5(频率中心)、p7(均方根频率)、p8(特征4)、p9(特征5)反映主频带位置的变化。


2.3 时频域特征提取
获得时域和频域特征集的确能较好地反映全寿命性能退化状况,但时域和频域特征主要表征线性信号特征,对于表征非线性信号呈现能力不足,而轴承运行过程较为复杂,其振动信号具有非线性特征。因此,仅采用时域和频域两种特征还不足以全面反映轴承性能退化趋势。时频域是表征非线性信号的一种特征指标,若与时域和频域特征共同构成集合则能全面反映轴承全寿命过程的运行状态。目前,小波包分析是一种时间窗和频率窗都可以改变的时频分析方法,可同时对信号进行低频和高频分解,实现非常精细的刻画,从而应用非常广泛。基于此,文中采用小波包分解并提取各频段能量作为轴承性能退化的时频域特征集,具体提取方法:
1)对预处理信号进行EEMD 分解、筛选与重构,然后选用db3 小波基函数进行3 层小波包分解得到8 个频段S3i(3 表示分解层数;i = 0,1,2,…,7,代表8 个频段位置)。
2)分别计算各频段的能量值,如式(20)所示:

式中xi,j为第i 个频段信号的离散点幅值,n 为采样点数。
3 基于PCA 加权融合多特征域的性能退化指标
上述分析的时域、频域和时频域特征均有诸多指标构成,若用单纯的某一指标来全面表征滚动轴承的衰退状况显然不合适。另外,因轴承全寿命的运行状态较为复杂,不同域特征集分布于空间不同的维度中,为此由不同维度的特征来表征轴承的运行特征也不合适,可见寻找众多域特征信息进行加权融合方法是十分必要的。目前,用于信息特征融合的方法主要有PCA 和流行学习算法,其中流行学习算法计算较为复杂,相比PCA 算法而言其稳定性不足。另外,流行学习算法在高维信息融合过程中参数选择对于信息融合的效果有很大影响。因此,文中选择稳定性较高的PCA 加权融合滚动轴承时域、频域和时频域多特征的性能退化指标集。PCA方法本质是通过坐标变换,实现用少数的主成分描述高维的数据,并将数据集转化为由维数较少的“有效”特征成分来表示,并且不减少原始数据所包含的信息内容,使其在统计意义下达到方差最优的目的。PCA 加权融合步骤如下:
1)提取滚动轴承的时域、频域和时频域的退化性能指标,将其构成数据矩阵X:

2)对矩阵X 标准化处理:
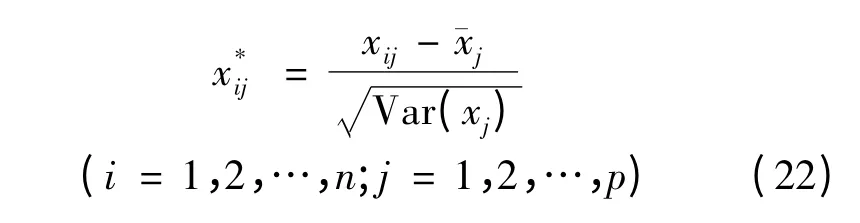
式中
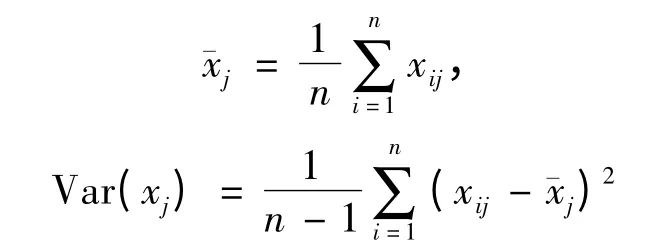
(j = 1,2,…,p)
3)计算退化性能指标的相关系数矩阵R:

式中,假定原始数据标准化后仍用X 表示,则经标准化处理后数据的相关系数为
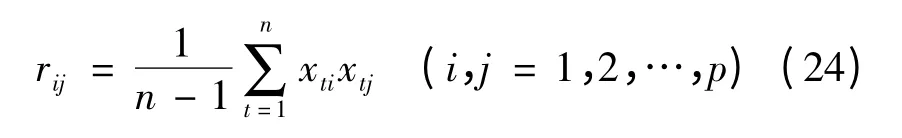
4)用雅克比方法求相关系数矩阵R 的特征值(λ1,λ2,…,λp)和相应的特征向量:
ai= (ai1,ai2,…,aip),i = 1,2,…,p
5)选择贡献率在85% 以上的主成分:

根据PCA 建立的衰退性能指标不难看出,PCA可以在最小化的数据情况下,将多个特征信息的冗余数据予以消除,并完整地反映滚动轴承的退化特征。
4 实验分析
4.1 实验装置
研究滚动轴承的性能退化过程,必须要有轴承全寿命周期的振动数据,这与传统的故障诊断研究存在本质区别。文中的实验数据[12]来自Cincinnati大学,其实验装置如图1 所示。装置中通过电动机带动轴上的4 个滚动轴承转动,其中每个滚动轴承分别在X 和Y 方向上安装ICP 加速度振动传感器。为了实现轴承加速疲劳寿命试验,在每个滚动轴承上均施加径向载荷26 670 N,轴承从开始运行至失效共持续7 d。实验中,电机转速恒为2 000 r/min,采样频率为20 kHz,共获得984 个文本(每个文本视为1 个数据点),每个文本包含20 480 个采样数据,每个文本之间有10 min 间隔。通过持续7 d 采集,共采集20 152 320 个数据,如图2(每隔10 个数据进行抽 取得到此图形)所示。

图1 滚动轴承全寿命数据采集装置Fig.1 Lifetime data acquisition device of the rolling bearing

图2 轴承运行的初始信号Fig.2 Initial signal of the bearing running
4.2 EEMD 预处理初始信号
采集的信号一般都有隐含的背景噪声,若不处理必定会对性能退化指标提取产生很大影响。文中采用EEMD 方法对初始信号进行分解、筛选和重构,从而达到降噪的目的。具体的实施过程为:对初始信号进行EEMD 计算,其中EEMD 算法中设置Rstd =0.2,添加高斯白噪声次数为1 000,分解得到如图3 所示的15 个IMF 分量和1 个残余分量,然后利用式(6)所示的相关系数准则分别计算15 个IMF分量与初始信号的相关程度,各IMF 分量的相关系数如表1 所示。根据经验公式[13],设定μ = 0.1,若IMF 分量相关系数小于阈值,则表明该IMF 分量与初始信号的相关系数过小,因此可以将该IMF 分量视为伪分量给予直接剔除。由表1 不难看出,IMF7~IMF15均小于0.1,从而将它们直接剔除,剩余的IMF1~IMF6再进行重构后得到新的初始信号。

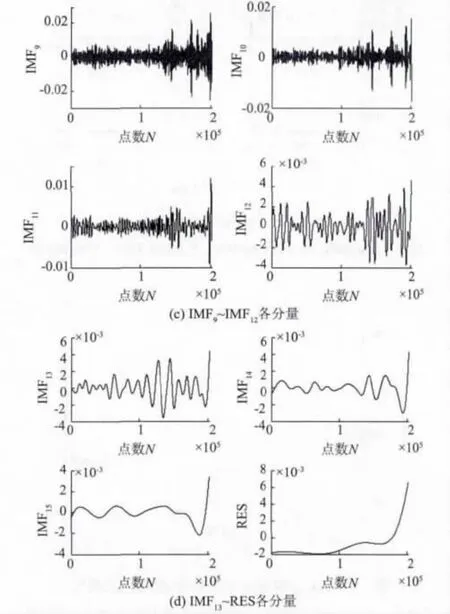
图3 EEMD 分解轴承信号情况Fig.3 EEMD decomposed bearing signal

表1 各IMF 分量的相关系数Tab.1 Correlation coefficient of each IMF component
4.3 建立加权融合多域特征的性能指标
根据时域指标数学表达式,分别建立16 个时域特征指标,如图4 所示。同理,根据式(7)至式(19)分别建立13 个频域特征指标,如图5 所示;根据式(20)分别建立小波包8 个节点的能量时频域特征指标,如图6 所示。由图4 ~6 不同域的性能退化指标曲线可以看出,有些指标对于性能退化敏感度很弱,如时域指标的均值、偏斜度和峭度,频域特征指标8,时频域指标的S34、S35 和S37 频带均是等到轴承快失效时才体现;有些指标过于信息嘈杂,如时域指标的峰值指标、脉冲指标、裕度指标、频域指标特征1 和特征2。对于敏感度太弱和信息过于嘈杂的性能指标都不适宜用于表征滚动轴承的性能退化状态,因此应将这些指标给予剔除,而其它保留下来的性能指标则通过PCA 方法进行加权融合,从而得到既代表轴承的退化趋势,又使维数得到约简的性能指标。图7 为PCA 加权融合各域性能指标的第1 主成分,不难看出,第1 主成分与各域单个的性能指标相比,性能指标得到改善:其一,信息不冗余,非常纯净;其二,提升了轴承退化的敏感度,PCA 加权融合之前,各域单一指标大部分在600 点左右才体现轴承退化趋势,加权后的性能指标在490 点左右就显现出轴承衰退趋势。可见,利用PCA 加权融合各域特征指标使冗余信息更纯净,能够全面表征轴承性能退化趋势,为后续剩余寿命预测研究奠定基础。
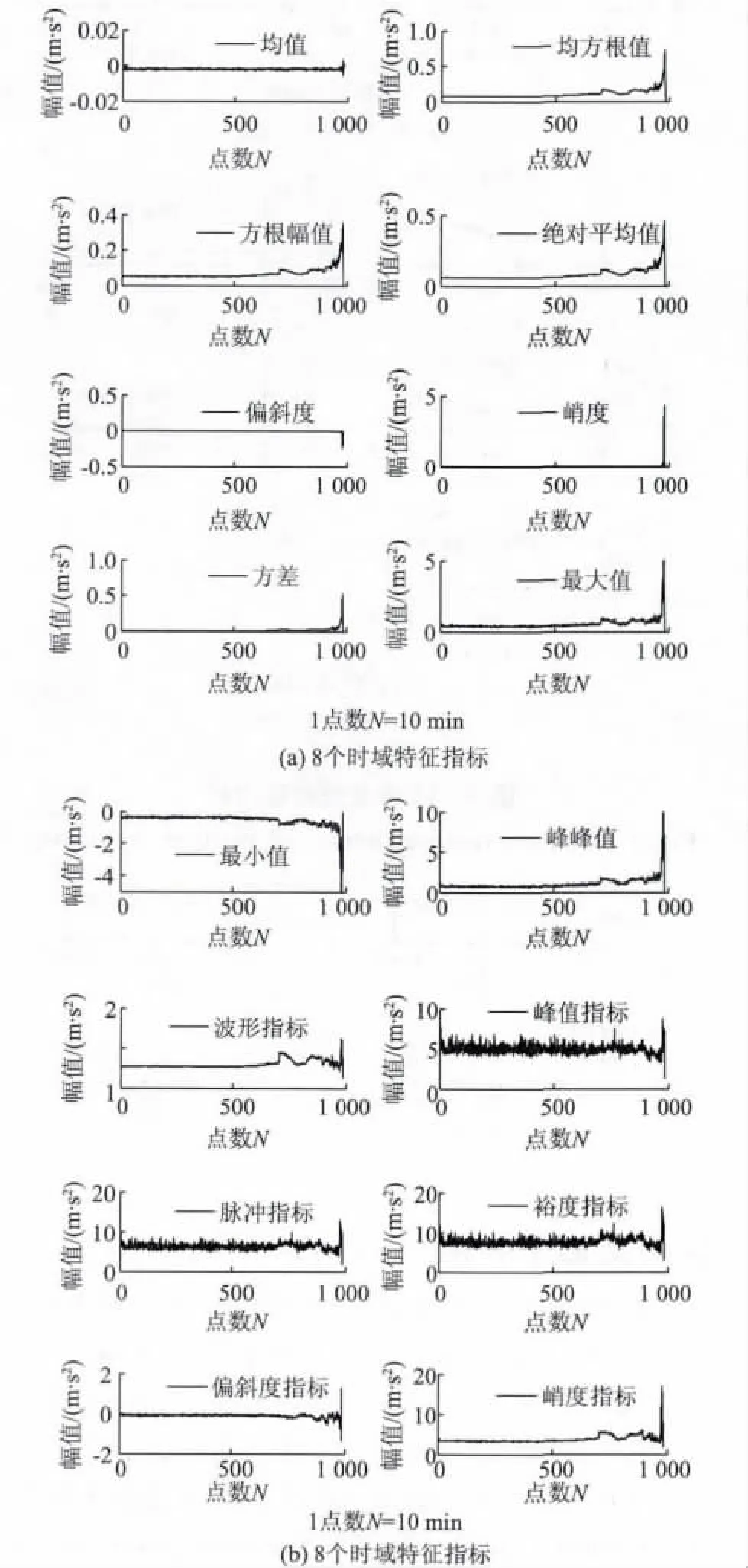
图4 16 个时域特征指标Fig.4 Feature indexes of sixteen time domain

图5 13 个频域特征指标Fig.5 Domain feature indexes of thirteen frequency

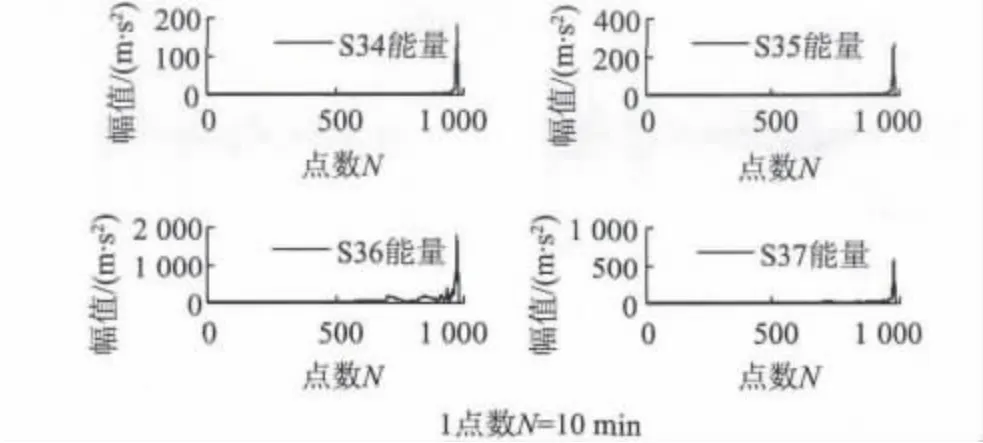
图6 8 个时频域特征指标Fig.6 Domain feature indexs of eight time -frequency

图7 PCA 加权融合多域特征的第一主成分Fig.7 First principal component of the PCA weighted fusion multi-domain feature
5 结 语
1)采用EEMD 分解,结合相关系数准则,提取相关程度高的IMF 分量,并重构有效IMF 各分量信息,从而实现了信号降噪。
2)建立时域、频域和时频域共37 个滚动轴承性能退化指标,剔除不适合表征退化趋势的指标后,采用PCA 方法加权融合其它指标,得到了更纯净且敏感度更高的退化性能指标。
3)获得的退化性能指标为滚动轴承的剩余寿命评估奠定了良好的基础。
[1]艾树峰.基于双树复小波变换的轴承故障诊断研究[J].中国机械工程,2011,22(20):2446-2451.AI Shunfeng. Research on bearing fault diagnosis based on dual-tree complex wavelet transform[J]. China Mechanical Engineering,2011,22(20):2446-2451.(in Chinese)
[2]徐东.球轴承疲劳剩余寿命分析与预测方法研究[D].长沙:国防科技大学,2011.
[3]徐小力,王红军.大型旋转机械运行状态趋势预测[M].北京:科学技术出版社,2011.
[4]Shichang D,Jun L,Lifeng X.Degradation process prediction for rotational machinery based on hybrid intelligent model[J].Robot Comput Integr Manuf,2012,28(2):190-207.
[5]肖文斌,陈进,周宇,等.小波包变换和隐马尔可夫模型在轴承性能退化评估中的应用[J]. 振动与冲击,2011,30(8):32-35.
XIAO Wenbin,CHEN Jin,ZHOU Yu,et al. Wavelet packet transform and hidden Markov model based bearing performance degradation assessment[J].Journal of Vibration and Shock,2011,30(8):32-35.(in Chinese)
[6]李巍华,李静,张绍辉.连续隐半马尔科夫模型在轴承性能退化评估中的应用[J].振动工程学报,2014,27(4):613-620.
LI Weihua,LI Jing,ZHANG Shaohui. Application of continuous hidden semi-Markov model in bearing performance degradation assessment[J].Journal of Vibration Engineering,2014,27(4):613-620.(in Chinese)
[7]王立,于重重,施彦,等.基于振动信号分析的电机性能退化特征提取[J].计算机仿真,2014,31(4):416-420.
WANG Li,YU Chongchong ,SHI Yan,et al.Degradation characteristics extraction of electric motor properties based on vibration signal analysis[J].Computer Simulation,2014,31(4):416-420.(in Chinese)
[8]董绍江.基于优化支持向量机的空间滚动轴承寿命预测方法研究[D].重庆:重庆大学,2012.
[9]WU Z H,HUANG N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1 -41.
[10]余发军,周凤星.基于EEMD 和自相关函数特性的自适应降噪方法[J].计算机应用研究,2015,32(1):206-209.
YU Fajun,ZHOU Fengxing.Adaptive de-noising method based on EEMD and autocorrelation function property[J]. Application Research of Computers,2015,32(1):206-209.(in Chinese)
[11]陈仁祥,汤宝平,吕中亮.基于相关系数的EEMD 转子振动信号降噪方法[J].振动、测试与诊断,2012,32(4):542-546.
CHEN Renxiang,TANG Baoping,LU Zhongliang.Ensemble empirical mode decomposition de-noising method based on correlation coefficients for vibration signal of rotor system[J].Journal of Vibration,Measurement and Diagnosis,2012,32(4):542-546.(in Chinese)
[12]Lee J,QIU H,YU G.Rexnord technical services“bearing data set”[R].Moffett Field,CA:IMS,University of Cincinnati,1990.
[13]边杰,王平,梅庆. EEMD 结合能量特征和小波降噪的轴承故障诊断[J]. 广西大学学报:自然科学版,2014,39(6):1206-1211.
BIAN Jie,WANG Ping,MEI Qing. Fault diagnosis of bearings by using EEMD combined with energy feature and wavelet denoising[J].Journal of Guangxi University:Nat Sci Ed,2014,39(6):1206-1211.(in Chinese)

