基于UKF 的铅酸蓄电池SOC 估算策略

胡振宇， 吴 雷

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡214122)

目前，国内外普遍使用不同的算法互相预测电池荷电状态(State of Charge，SOC)，该方法是由模糊判别和精确计算构成。SOC 估算方法有:开路电压法、安时计量法、神经网络和卡尔曼滤波法(Kalman Filtering，KF)［1］。安时计量法有两个明显的缺点:电流不精确，充放电效率难以确定［2］。KF作为SOC 估计的一个集成平台，主要通过电池SOC和外部参数之间的映射(包括电流、电压和电池温度等)解决SOC 估计。这种映射是一种非线性关系，在建立准确适用的电池动态模型上存在很大困难，常见的KF 不能解决这个问题［3］。

1 Thevenin 模型建立

适合UKF 滤波估计的电池模型必须能较好地体现电池的动态性能，同时阶数不能太高，易于实现［5］。

在运用卡尔曼滤波算法估算SOC 时，首先要建立适合于卡尔曼滤波方法的电池模型［6］。动力电池常处于电流剧烈变化的特殊工况中，且充放电非常频繁，温差大。鉴于以上考虑选择如图1 所示的Thevenin 模型。其中，E(t)为电动势，I(t)为电流，R1为电池的欧姆内阻;R2为电池极化内阻，与电容C 并联形成阻容回路，用于模拟电池的动态特性［7］。

图1 Thevenin 电池模型Fig.1 Tevenin battery model

2 UKF 等式

UKF 算法是典型的非线性变换估计［8］。非线性变换后，它仍然是一个标准的卡尔曼滤波。算法的核心是通过U 转换(无味变换)进行非线性模型状态误差协方差递归和更新。UKF 能准确估计均值并使协方差达到四阶泰勒级数，可以满足基本需求的铅酸电池SOC 估计。该方法关键是通过非线性的U变换进行非线性模型与误差协方差的递推和更新。

2.1 UKF 状态方程

在这个SOC 算法中，系统状态方程为安时法，以下是离散方程

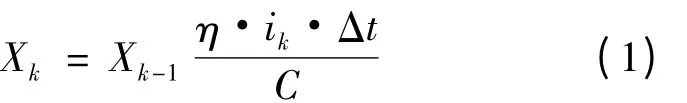
其中，Xk表示SOC 值的系统状态;k 为时间步，可以从上一步k －1 测量电池电流，根据当前时间步k，计算当前采样周期积分值Δt。添加库仑效率η 和电池额定容量C，可以计算Xk。安时法计算模型的计算精度直接影响η 与C。

2.2 电池额定容量的变量模型

C 不是一个常数，而是相当于额定容量的一个变量。文中使用一个变量命名变量额定容量，以反映真实的额定容量。可变容量的值与主要生产铅酸电池的额定容量有关，电池正面和负面活动材料的数量和利用率，活性物质的利用率主要受3 个因素的影响。放电机制:包含放电速率I，放电形式，终止电压U，电池温度T;电极的结构:包括电极高宽比例、厚度、空隙率、以及导电栅网形式;制造工艺。此外，放电机制是可变因素，其他两个因素是不可变的因素。所以，额定容量可以表示为一个变量函数。电池使用后，不可再生因素会出现，如活性物质脱落，电极结构改变。铅酸电池的额定容量应修改如下:

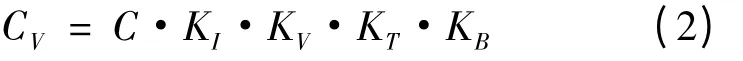
式中:KI为电流影响因子;KV为电压影响因子;KT为电池温度影响因子;KB为不可恢复因素影响因子。

在这些参数中，C 相当于电池额定容量。系数KT可以通过公式推导

截至2014年年底，全国有效使用绿色食品标志企业总数达到8700家，产品21153个，达到历史新高。2014年上半年统计数据显示，绿色食品大米、水果和茶叶产量已分别占全国大米、水果和茶叶总产量的10.8%、6.8%和3.7%。全国共创建了635个绿色食品原料标准化生产基地，基地种植面积1.6亿亩。

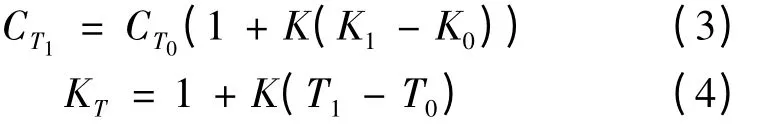
其中，T0为在25 ℃的基准温度;T1为当前电池温度;K 为由特定电池型号所决定的温度影响因素;KV= 1 是理想值，因为临界电压在实验中是保持不变的;KB从实际可变容量和预计可变容量之间获得;KI可通过不同的放电率下的电池实验获取，0 ＜KI＜1。

2.3 电池的库伦效率

为了获得库伦效率η，文中使用Peukert 推导公式

然而，这个Peukert 方程并不能准确反映当前和库仑效率之间的关系，因为在高放电电流状态时有一个大偏差出现。p 作为变量，计算库仑效率。在上述修正后，变量电池额定容量的概念更清楚，简单、准确的安时估计已成为可靠的计算方法。最后的系统状态方程可以改写为

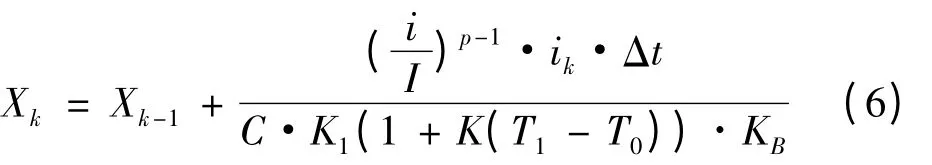
结合负载电压方法的特点，获得以下负载电压模型算法测量方程:

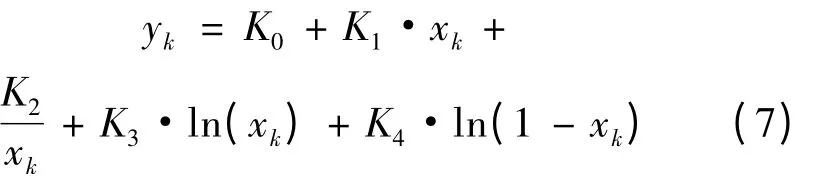
3 UKF 算法

3.1 具体SOC 算法流程

结合式(6)和式(7)，可以得到基于UKF 的SOC 算法。算法变量Xk和Yk分别为过程噪声和测量噪声;Q 为过程噪声协方差;R 为测量噪声协方差［9］。具体的算法设计过程如下:

1)初始化

2)Σ 计算点

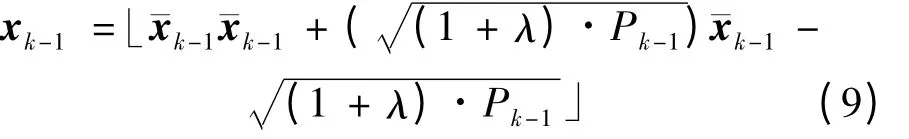
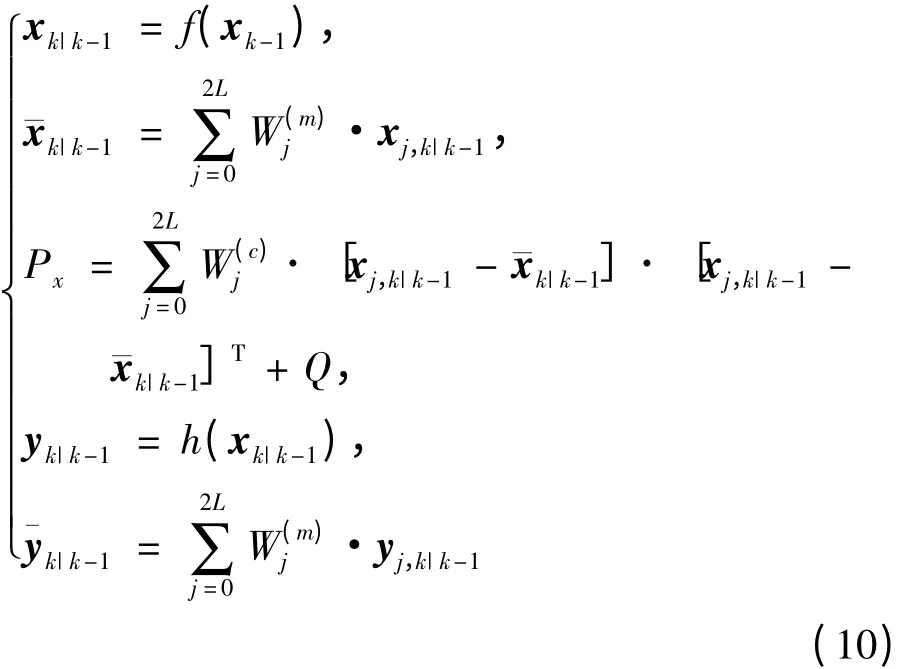
3)时间更新

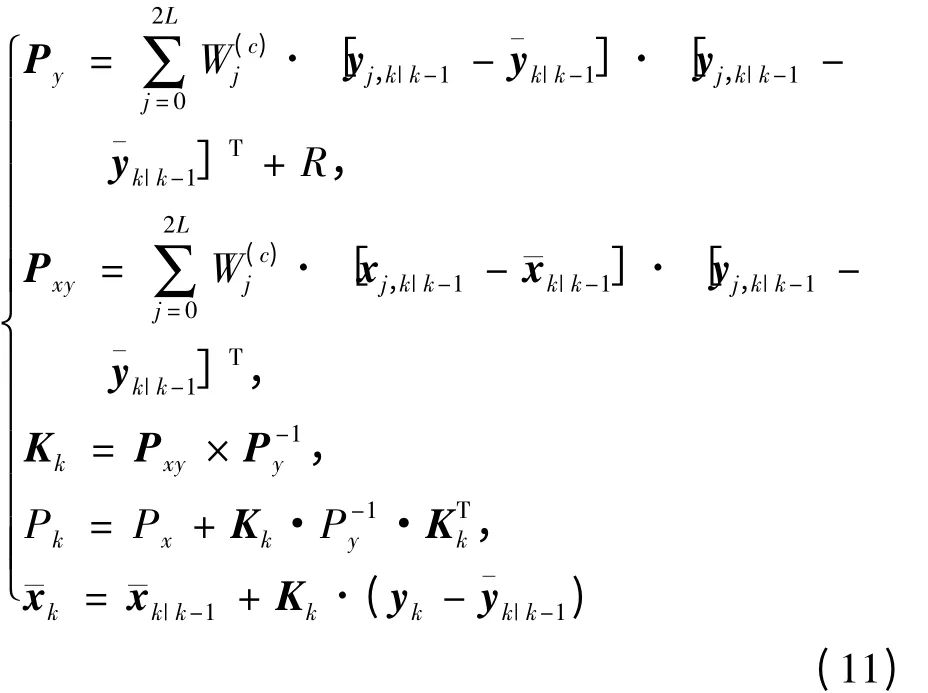
4)测量更新方程

3.2 对应关系

电池在长时间静置的条件下，其端电压与SOC有相对固定的函数关系。所以根据开路电压可以估计SOC，特别是在充放电的初期和末期，电池端电压变化较大，开路电压法可以取得较好的效果［10］。图2 为开路电压与SOC 之间的关系。在文中以天能3－EVF－200 铅酸电池为实验对象，使用大功率放电电阻和2.5 kW 充电器获取实验数据。

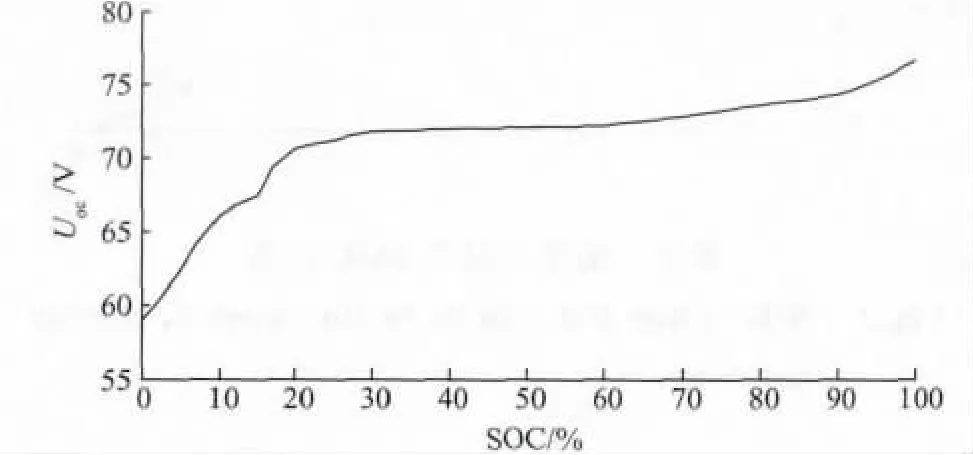
图2 开路电压与SOC 之间的关系Fig.2 Relationship between the open circuit voltage and the SOC

为了得到状态方程，需要测试系数等式(2)。以解决系数KI为例。在同等条件下，电池在C6，C5，C4，C3情况下呈现出不同放电曲线。曲线反映了剩余容量和放电率之间的关系，在曲线中能得到不同放电率下的值。

给定参数值后，得到数据变量额定容量(见表1)。由表1 可以看出，预测容量值非常接近手册给定真实值的。因此，该变量(变量电池额定容量)才能真正反映铅酸电池额定容量的变化。利用实验数据，通过回归方法，可以得到在式(7)中K0，K1，K2，K3，K4的值。

表1 电池容量Tab.1 Battery capacity

4 仿真实验

为了验证这种SOC 算法的有效性，文中进行了包括恒流充电，恒压和脉冲充电/ 放电实验。图3 为在恒流条件下SOC 状态，图4 为恒流条件下估算绝对误差。

采用开路电压法计算SOC 值，将此值作为电池的真实SOC，与实验数据进行对比。在初始预测阶段，SOC 估算值在真值范围内波动，SOC 实验和SOC误差迅速增加，直到达到最大。最后阶段，估计价值逐渐收敛于真值。在整个变化过程中，SOC 最大误差不超过4%，平均误差小于2%。

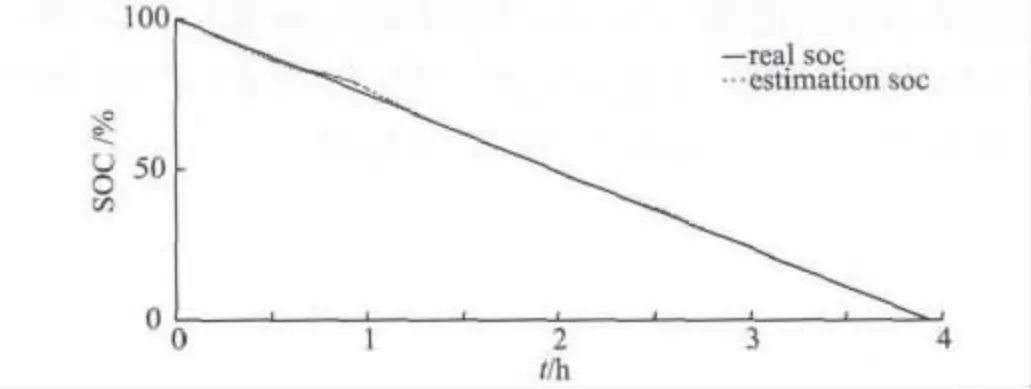
图3 恒流工况下SOC 状态Fig.3 SOC value test results in the constant-current condition

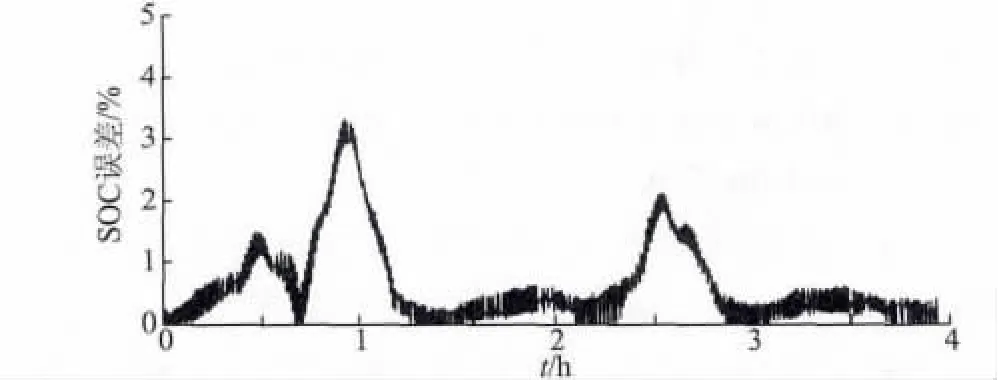
图4 恒流工况下估算绝对误差Fig.4 SOC absolute error results in the constantcurrent condition

脉冲工况下SOC 状态及估算误差如图5 和图6所示。

在图5 中，脉冲充电/放电电流为20 A，SOC 估计在真值范围波动。估计值和真值之间的变化速度并不一致。每一个脉冲周期包含4 个阶段:在充电阶段，估算值迅速接近真实价值并达到最大值;在保持阶段后电池充电，估算值迅速从最大值降低至最小值;在放电阶段，估算值是最小值附近的真值;在保持阶段后电池放电，估算值更接近真实价值。究其原因，电池电压在第1 阶段和第2 阶段迅速上升，两个阶段之间有很大的电压差;相反，电压在第3 阶段上升放缓，最后两个阶段之间的电压差减小。在所有这些脉冲周期，SOC 最大误差不超过5%，UKF算法能够更好地估计脉冲充电/ 放电状态。基于这些结果在上面3 种情况可以得出这样的结论:UKF算法的SOC 估计误差不超过5%，算法稳定性好。因此，该算法是一种有效的铅酸电池SOC 估计算法。

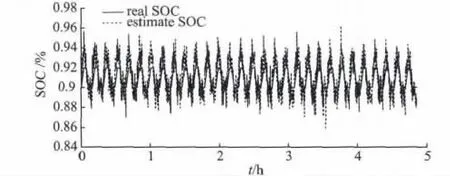
图5 脉冲工况下SOC 状态Fig.5 SOC value test results in the pulse-charge/discharge condition

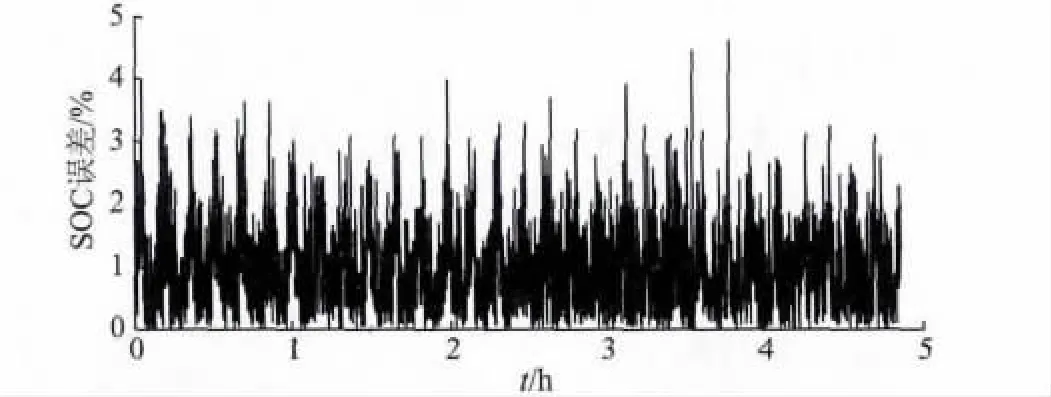
图6 脉冲工况下估算误差Fig.6 SOC absolute error results in the pulse-charge/discharge condition

5 结 语

在建模方面文中采用Thevenin 模型，考虑电流，电压，温度等因素对SOC 估算的影响;在算法上，采用UKF 算法容易实现并且有较高的状态估计精度。可以预见，基于适合的电池等效模型，UKF 在铅酸蓄电池SOC 估计方面有着广阔前景，因此进一步实现基于UKF 的SOC 估算方法的工程化是很有必要的。

［1］林成涛，陈全世，王军平，等.用改进的安时计量法估计电动汽车动力电池SOC［J］.清华大学学报:自然科学版，2006，46(2):247－251.

LIN Chengtao，CHEN Quanshi，WANG Junping，et al.State of Charge estimation salibration for Ni－MH［J］.Journal of Tsinghua University:Science and Technology，2006，46(2):247－251.(in Chinese)

［2］高玉峰，孙磊，刘亚龙，等.基于EKF 算法的铅酸蓄电池SOC 在线估计［J］.电源技术，2012，38(2):303－306.

GAO Yufeng，SUN Lei，LIU Yalong，et al.Estimating SOC of lead－acid battery based on Extented Kalman Filtering［J］.Chinese Journal of Power Source，2012，38(2):303－306.(in Chinese)

［3］田晓辉，刁海南.车用锂离子动力电池SOC 的预测研究［J］.电源技术，2010，34(1):51－54.

TIAN Xiaohui，DIAO Hainan.Research on estimation of lithium－ion battery SOC for electric vehicle［J］.Chinese Journal of Power Sources，2010，34(1):51－54.(in Chinese)

［4］李哲，卢兰光，欧阳明高.提高安时积分法估算电池SOC 精度的方法比较［J］.清华大学学报:自然科学版，2010，50(8):1293－1296.

LI Zhe，LU Languang，OUYANG Mingao.Comparison of methods for improving SOC estimation accuracy through an ampere－hour integeration approach［J］.Journal of Tsinghua University:Science and Technology，2010，50(8):1293－1296.(in Chinese)

［5］于海芳，逯仁贵.基于安时法的镍氢电池SOC 估计误差校正［J］.电工技术学报，2012，27(6):12－18.

YU Haifang，LU Rengui. State of Charge estimation calibration for Ni－MH［J］. Transactions of China Electrotechnical Society，2012，27(6):12－18.(in Chinese)

［6］潘卫华，刘晓丹.基于改进卡尔曼滤波的锂电池SOC 估算研究［J］.计算机仿真，2014，31(3):148－150.

PAN Weihua，LIU Xiaodan.Research on estimating SOC of lithium－ion battery based on improved Kalman Filter［J］.Computer Simulation，2014，31(3):148－150.(in Chinese)

［7］吴红杰，齐铂金，郑敏信.基于Kalman 滤波的镍氢动力电池SOC 估算方法［J］. 北京航空航天大学学报，2007，33(8):945－948.

WU Hongjie，QI Bojin，ZHEN Minxin. Ni－MH battery state of charge estimation based on Kalman Filter［J］. Journal of Beijing University of Aeronautics and Astronautics，2007，33(8):945－948.(in Chinese)

［8］夏超英，张术，孙宏涛.基于推广卡尔曼滤波算法的SOC 估算策略［J］.电源技术，2007，131(5):414－417.

XIA Chaoying，ZHANG Shu，Sun Hongtao.A strategy of estimating state of charge based on extended kalman filter［J］.Chinese Journal of Power Sources，2007，131(5):414－417.(in Chinese)

［9］WAN E A ，van der Merwe R.The Unscented Kalman Filter for nonlinear estimation［C］//Adaptive Systems for Signal Processing，Communications，and Control Symposium.Portland，US:IEEE，2000:153－158.

［10］黎夏.电动汽车铅酸蓄电池充电器研制［D］.杭州:杭州电子科技大学，2013.