基于改进的形态学滤波和EEMD 方法的滚动轴承故障诊断

宗永涛， 沈艳霞 ， 纪志成

(江南大学 电气自动化研究所，江苏 无锡214122)

齿轮箱一旦发生故障，将会使设备损坏、发电机停机，由此带来严重的经济损失［1］。轴承是齿轮箱的重要组成部分，它的工作状况将影响整个电机的性能。由于其运行环境、负荷及时间的影响，故障率极高。当滚动轴承发生故障时，会产生周期性的脉冲信号，从而导致调制信号的产生。轴承故障振动信号是非线性、非平稳信号，并且常常被大量的随机噪声所淹没，这给分析故障带来巨大困难，因此，如何在噪声背景下提取冲击故障特征是滚动轴承故障诊断的关键［2］。

针对滚动轴承的故障，国内外学者提出了不同的诊断方法，如快速傅里叶变换，维格纳分布、小波分析等，田广等［3］针对行星齿轮箱滚动轴承故障提出基于伪Wigner-Ville 分布方法，可直观反映出轴承故障的时频域信息，得到比较理想的诊断结果;ZHANG H［4］采用连续的小波变换方法有利于提取更微弱的故障信息，应用在滚动轴承滚道缺陷和齿轮裂纹的识别中诊断效果较为理想。由于此类方法是重要的非平稳信号处理方法，都有较好的时频分析效果，可以更好地提取故障特征信息，一定程度上满足了非平稳信号时频分析的要求;然而它们都受Heisenberg 测不准原理的制约，存在局限性。为此，HUANG 等［5］提出经验模态分解(EMD)方法将非平稳信号分解为有限个不同尺度的固有模态函数及趋势项之和，具有自适应的信号分解和降噪能力，是一种新的分析非线性、非平稳信号的时频方法［6］。但EMD 方法存在模态混叠现象，大大限制其它在实际中的应用，为此HUANG 对其进行了改进，提出了EEMD(集合经验模态分解)信号分解方法［7］，利用高斯白噪声具有频率均匀分布的统计特性，使加入高斯白噪声后的信号在不同尺度上具有连续性，从而有效地解决经验模态分解中的模态混叠问题［8］。近年来，该方法得到了广泛的应用。如李辉等［9］利用EEMD 和THT 变换对齿轮箱进行了故障诊断;朱宁辉等［10］将EEMD 方法应用于谐波检测中的应用。

由于齿轮箱振动信号往往不可避免地受到噪声的干扰，反映故障信息的微弱脉冲很容易被淹没，给进一步的EEMD 分解带来困难。虽然小波变换目前应用广泛，但小波变换存在着众多的小波基函数，而各小波基函数的适用范围并不一致，这就造成了小波基选择问题。数学形态学［11］是基于积分几何和随机集论建立起来的非线性图像(信号)处理和分析工具，该方法进行信号处理时只取决于待处理信号的局部形状特征，通过数学形态变换将一个复杂的信号分解为具有物理意义的各个部分，并将其与背景分离，同时保持信号主要的形态特征。该方法与其他非线性滤波器相比，具有平移不变性、单调性、幂等性等特性，且计算简单、运行速度快。因此，近年来数学形态学逐渐被引用到一维信号处理领域(如电力系统、语音、心电以及振动信号处理中［12-13］。

文中将改进的形态滤波与EEMD 方法相结合，首先设计一种基于递归最小二乘法(RLS)算法的自适应形态滤波器对原始信号进行消噪处理，然后通过互相关系数方法消除EEMD 分解结果中包含的虚假分量，从而得到更准确的Hilbert-Huang 谱，由此提取故障信息，准确地判断故障类型及故障发生的位置。

1 轴承故障诊断

1.1 诊断流程

当滚动轴承出现故障时，会产生突变的冲击脉冲力和周期性的脉冲信号，从而导致调制信号的产生;同时由于风机所处的环境，其振动信号往往不可避免的受到噪声的干扰，反映故障信息的脉冲很容易被淹没，为分析故障带来困难。因此，如何在强噪声背景下提取冲击故障特征是滚动轴承故障诊断的关键。对于含有严重噪声的原始振动信号，采用数学形态学滤波方法，先通过自适应形态滤波器对轴承故障振动信号进行消噪预处理，去除信号中的噪声成分，同时保持其主要的形态特征，显著增强故障特征，便于进一步的故障诊断。采用EEMD方法根据振动特性，按照从高频到低频的顺序分解为具有不同振动模态的子成分，从而有效地将信号中的噪声成分分离，通过相关系数方法去除虚假分量，对保留下来的IMF 分量作Hilbert-Huang 谱可有效地提取故障特征。文中提出自适应形态滤波和EEMD 方法相结合的滚动轴承故障诊断策略。滚动轴承故障诊断的流程如图1 所示。

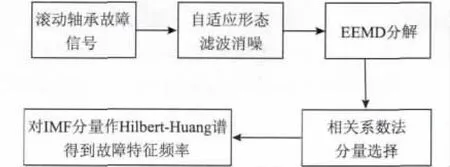
图1 滚动轴承故障诊断流程Fig.1 Flowchart of the rolling bearing fault diagnosis

1.2 形态学滤波器设计

数学形态学是一种非线性图像(信号)处理和分析工具。数学形态学以集合描述目标信号，其思想是设计一个称作结构元素的“探针”相当于滤波窗，收集信号的信息，通过该探针在信号中不断移动，对信号进行匹配，以达到提取信号、保持细节和抑制噪声的目的。数学形态学包括:腐蚀和膨胀［14］两种基本运算，并在此基础上构造出的开运算、闭运算等。

假设风机齿轮箱滚动轴承故障振动信号f(n)为定义在F = (0，1，…，N －1)上的一维离散函数，定义结构元素g(n)为G = (0，1，…，M －1)上的离散函数，且N ≥M，则f(n)关于g(n)的腐蚀和膨胀分别定义为

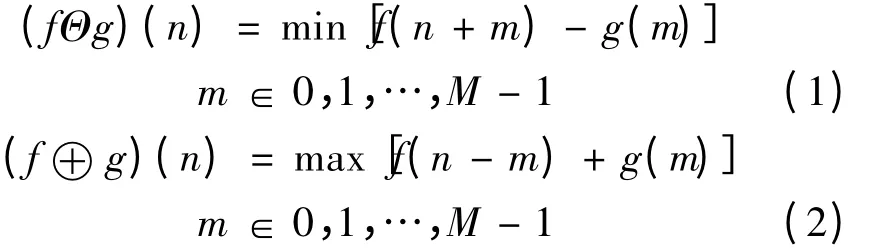
f(n)关于g(n)的开运算和闭运算分别定义为

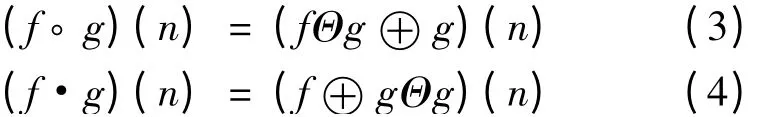
进而得到形态开-闭和闭-开运算:

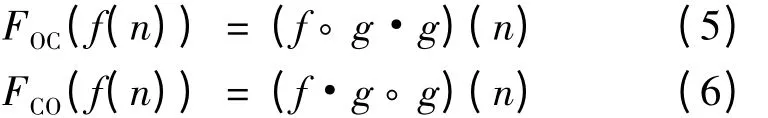
其中，符号◦和·分别表示开运算和闭运算。开运算使目标轮廓光滑，并去掉毛刺点和孤立点，它可以抑制信号中的峰值(正脉冲)噪声;闭运算则可以平滑或抑制信号下方的低谷(负脉冲)噪声。通过不同组合构成的滤波器可以对信号进行不同噪声的滤除。

1.2.1 自适应形态学滤波器的构建 形态开、闭运算级联组合形成的形态开-闭及闭-开滤波器具有开闭运算的所有性质，因此可以同时滤除信号中的正、负脉冲噪声。但由于开运算的收缩性导致开-闭滤波器的输出偏小，闭运算的扩张性导致闭-开滤波器的输出偏大，因而存在统计偏倚现象，直接影响到滤波器的噪声抑制性能，所以单独使用它们并不能取得较好的滤波效果。为了有效地抑制信号中的各种噪声，采用级联开、闭运算，结合自适应处理方法，提出一种自适应加权组合形态滤波器［15］用于滚动轴承故障振动信号的降噪。其结构如图2所示。

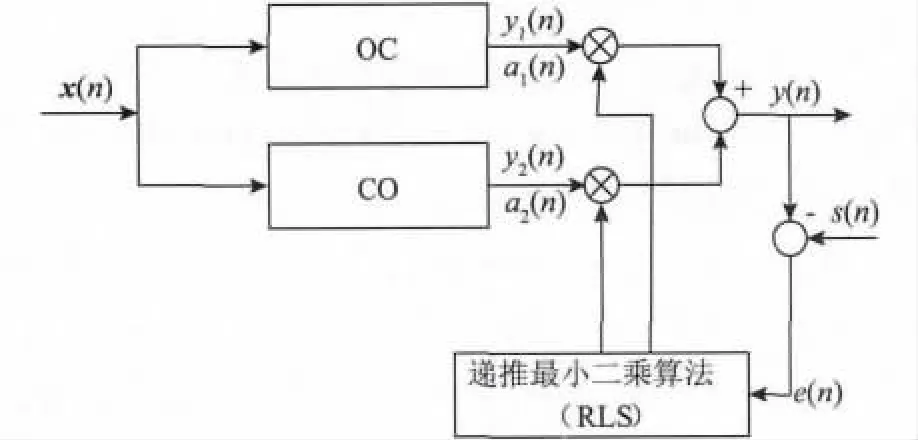
图2 自适应形态滤波器原理Fig.2 Principle diagram of the adaptive generalized morphological filter

设原始振动信号为

其中，s(n)为无噪声的理想信号;d(n)为噪声。y(n)为滤波器输出信号，e(n)为理想信号s(n)与滤波器输出信号y(n)间的误差信号，即

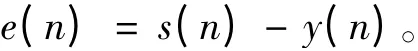
令

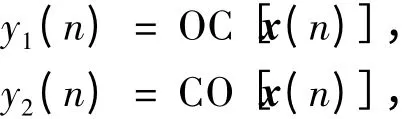
则自适应加权组合形态滤波器的输出为

这里相应的最小二乘准则的代价函数为

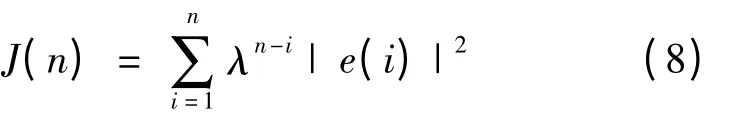
其中，λ 为加权因子。

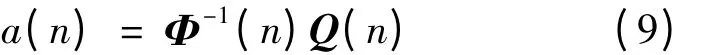
式中

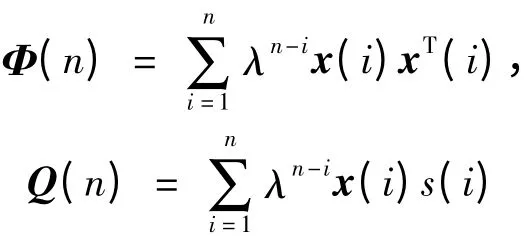
分别为自相关矩阵和互相关矩阵。

令C(n)= Φ－1(n)，由Φ(n)的递推关系和矩阵逆引理可得

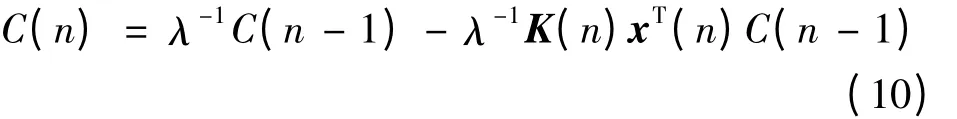
式中

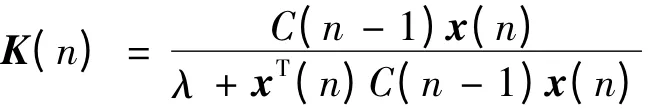
为增益向量。

由式(9)、式(10)的递推关系可得

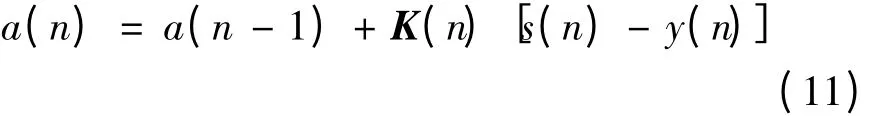
1.2.2 结构元素的选取 确定形态学滤波器的运算方式后，所选取的结构元素就是影响滤波器输出的主要因素。形态滤波的效果与所采用的结构元素有着密切的关系，结构元素的设计要能尽量接近待分析信号的形态特征。一般只有与结构元素的尺寸和形状相匹配的信号才能被保留。对于振动信号的处理，三角形、圆形、直线形3 种形状的结构元素均取得较好的滤波效果，其中以三角形结构元素处理效果最好，因此文中选择的结构元素为三角形结构元素。

1.3 故障信号的EEMD 分解

传统的经验模态分解方法，由于异常事件的存在，导致物理过程的重叠，即产生本征模态函数的模态混叠问题。EEMD 可以将任意非线性、非平稳信号分解为若干具有不同振动模态的本征模态函数(IMFs)和余项，巧妙地应用了高斯白噪声具有频率均匀分布的统计特性，向滚动轴承故障信号中加入高斯白噪声后，信号将在不同尺度上具有连续性，这样可以促进抗混分解，避免了EMD 方法中由于IMF 的不连续性而造成的模态混叠现象。本征模态函数需要满足以下两个条件:

1)在整个数据段内，极值点的个数和过零点个数必须相等或最多相差一个;

2)由它的极大值和极小值确定的上下包络线关于时间轴局部对称。

运用EEMD 分解方法对滚动轴承故障信号进行处理的步骤为:

1)在原始振动信号中多次加入高斯白噪声序列，形成混入白噪声信号集合:

2)对故障信号xi(n)求取局部极大值和局部极小值，利用插值方法求取对应的上、下包络线。xi(n)与上、下包络线均值mi1(n)的差记为hi1(n)，即

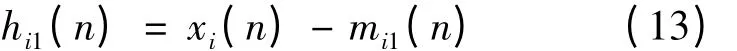
3)若hi1(n)满足IMF 条件，那么hi1(n)就是第1 个IMF 分量;若不满足，则把hi1(n)作为原始数据，重复执行筛选过程，直至hik(n)满足条件。记ci1(n)= hik(n)。

4)将ci1(n)从原始信号xi(n)中分离出来，得到一个余量信号ri1(n):

将ri1(n)作为原始数据重复以上过程，可以通过多次筛选逐个分解出有限个IMF 分量，即ci1(n)，ci2(n)，…，cik(n)。

5)对步骤1)中获得的下一个混入白噪声信号同样经过步骤2)～4)，获得各自的本征模态函数。

6)将上述对应的IMF 进行总体平均运算，以消除多次混入白噪声对真实本征模态函数的影响，最终得到的EEMD 分解后的IMF 为

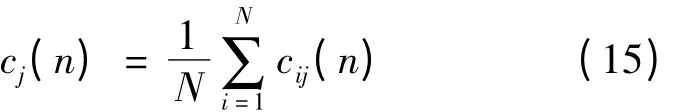
其中，cj(n)为对原始振动信号进行EEMD 分解后所得到的第j 个IMF。

EEMD 中所加高斯白噪声的次数服从的统计规律。其中:N 为总体的个数;a 为高斯白噪声的幅度;en为原始信号与由最终的IMF 加和得到的信号之间的误差。在噪声幅度一定的情况下，总体个数越多，最终分解得到的结果越接近真实值。对于所加噪声的幅度，如果幅度过小，信噪比过高，噪声将无法影响到极点的选取，进而失去补充尺度的作用。一般情况下，a 取0.2，N 取100。

1.4 虚假分量IMF 的消除

EEMD 把信号分解成特征时间尺度由小到大、频率由高到低的一系列IMFs 分量和一个余项，由于其自身分解规则的缺陷将导致虚假分量的产生，为此，可以用每个IMF 与原始信号的相关系数μ 的大小判断虚假IMF 与真实IMF。为避免幅值较小但确实是真实的IMF 被去除，需对所有的IMFs 和原始信号数据进行归一化处理。计算归一化后的IMF(n)与原始信号x(n)之间相关系数为

其中，i = 1，2，…，n，n 为IMF 的个数。虚假分量与真实分量的判断阈值λ 定义为

其中，η 为比率因子，η = 10。若相关系数μi＞λ，则认为其对应的IMF 为真实分量，将其保留;反之则为虚假的分量，将其去除。

2 实例验证及结果分析

当滚动轴承存在疲劳剥落故障时，滚动体旋转遇到一个局部缺陷，就会产生一个冲击信号。滚动轴承故障振动信号来自Case Western Reserve University 轴 承 数 据 中 心［16］， 轴 承 型 号 为SKF6205-2RS，转速为1 797 r/min，滚动体个数为9，滚动体直径为7.94 mm，节圆直径为39.04 mm，接触角为0。根据上述参数计算得出外圈故障特征频率为107.3 Hz。振动信号由加速度传感器采集，采样频率为12 kHz。图3 为轴承外圈原始振动信号的时域波形。

由图3 可以看出，该振动信号中不仅有滚动轴承固有振动信息，还混有复杂的噪声信息。对其进行EEMD 处理，得到如图4 所示的10 个IMFs 分量;再采用相关系数方法剔除多余的虚假分量，对保留下来的IMFs 分量作Hilbert-Huang 谱，所得结果如图5 所示。

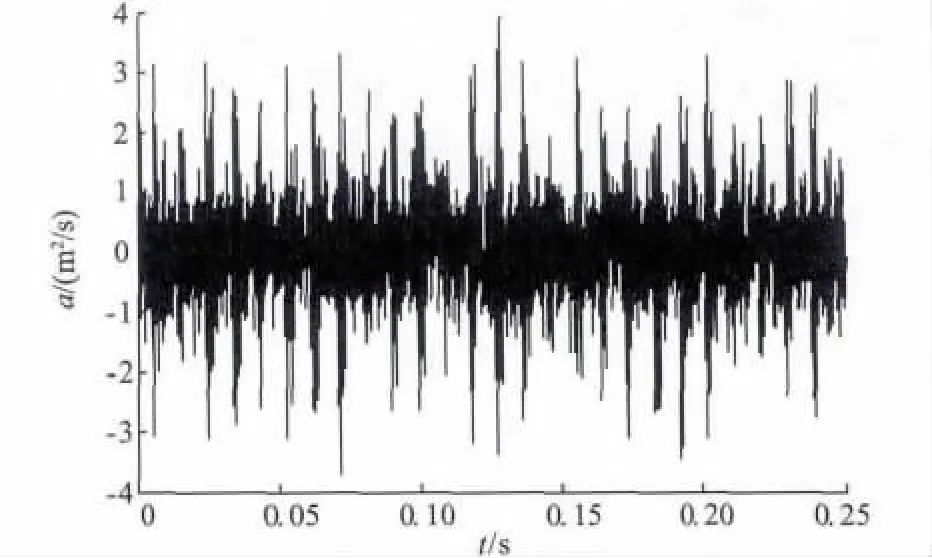
图3 外圈故障信号Fig.3 Outer race fault signal

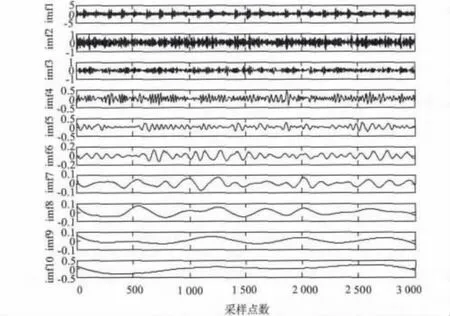
图4 原始信号EEMD 分解得到的各阶IMFs 分量Fig.4 IMFs decomposed by EEMD for the original signal

图5 外圈故障信号Hilbert-Huang 谱Fig.5 Hilbert-Huang spectrum of the outer fault signal

由图5 可以看出，周期性的瞬态冲击特性不明显，故障特征分辨率低。

为提取轴承故障特征，采用三角形结构元素，采用基于RLS 算法的自适应形态滤波器对故障振动信号进行降噪处理，然后通过EEMD 方法对故障信号进行分解，得到各阶IMFs 分量如图6 所示;再采用相关系数方法剔除多余的虚假分量，对保留下来的IMFs 作Hilbert-Huang 谱，具体结果如图7所示。

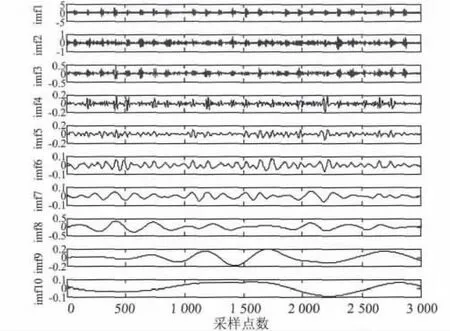
图6 形态滤波降噪后EEMD 分解得到的IMFs 分量Fig.6 IMFs decomposed by EEMD after filtering noise

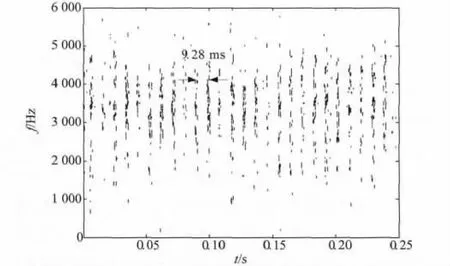
图7 外圈故障信号降噪后的Hilbert-Huang 谱Fig.7 Hilbert-Huang spectrum of the denoised outer fault signal

由图7 可以看出，该谱图中存在明显的周期性冲击成分，相邻两个冲击之间的时间间隔约为9.28 ms，可得冲击的频率约为107.76 Hz，接近外圈故障特征频率，因此可判断轴承外圈出现局部损伤。

表1 为3 种形态滤波器对外圈故障信号处理得到的信噪比SNR 和均方根误差RMSE。信噪比主要侧重于信号消噪前后功率的对比度，均方根误差则主要侧重于评价波形的失真度。

表1 各滤波器输出的SNR 和RMSETab.1 SNR and RMSE of three filters

由表1 可以看出，自适应形态滤波器消噪效果要优于其他两种形态滤波器。

3 结 语

为解决滚动轴承故障特征提取的问题，文中设计一种基于RLS 算法的自适应形态滤波器对故障振动信号进行消噪处理，然后利用EEMD 自适应地将信号分解为多个分量，再采用相关系数方法剔除多余的虚假分量，对保留下来的IMF 分量作Hilbert-Huang 谱，有效地提取故障特征。诊断结果表明，噪声对EEMD 分解影响很大，形态滤波降噪减少了噪声的干扰，提高了EEMD 分解的精度，得到了更准确的Hilbert-Huang 谱，准确地提取故障信息。基于自适应形态学滤波和EEMD 的方法具有较强的去噪能力，方法易于实现，实时性好，适用于周期脉冲故障信号特征提取。

［1］陈雪峰，李继猛，程航，等.风力发电机状态监测和故障诊断技术的研究与进展［J］.机械工程学报，2011，47(9):45-52.

CHEN Xuefeng，LI Jimeng，CHENG Hang，et al.Research and application of condition monitoring and fault diagnosis technology in wind turbines［J］.Journal of Mechanical Engineering，2011，47(9):45-52.(in Chinese)

［2］张弦，王宏力.进化小波消噪方法及其在滚动轴承故障诊断中的应用［J］.机械工程学报，2010，46(15):76-81.

ZHANG Xian，WANG Hongli. Evolutionary wavelet denoising and its application to ball bearing fault diagnosis［J］. Journal of Mechanical Engineering，2010，46(15):76-81.(in Chinese)

［3］田广，唐力伟，栾军英，等.基于时频分布的行星齿轮箱滚动轴承故障诊断研究［J］.机械强度，2007，29(1):152-155.

TIAN Guang，TANG Liwei，LUAN Junying，et al. Application of fault diagnosis based on time-frequencydistritution to rolling bearings of planetary gear box［J］.Journal of Mechanical Strength，2007，29(1):152-155.(in Chinese)

［4］ZHENG H，LI Z，CHEN X，et al.Gear fault diagnosis based on continuous wavelet transform［J］. Mechanical Systems and Signal Processing，2002，16(2/3):447-457.

［5］HUANG N E，SHEN Z，LONG S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London A，1998，454:903-909.

［6］祁克玉，施坤林，霍鹏飞，等.EMD 端点效应处理在转子摩擦故障诊断中的应用［J］.振动、测试与诊断，2010，30(5):492-495.

QI Keyu，SHI Kunlin，HUO Pengfei，et al.EMD boundary processing method and its application to friction fault diagnosis of rotor system［J］.Journal of Vibration Measurement and Diagnosis，2010，30(5):492-495.(in Chinese)

［7］WU Z H，HUANG N E. Ensemble empirical mode decomposition:a noise assisted data analysis method［J］. Advances in Adaptive Data Analysis，2009，1(1):1-41.

［8］ZHANG J，YAN R，FENG Z.Performance enhancement of ensemble empirical mode decomposition［J］. Mechanical Systems and Signal Processing，2010，24(7):2104-2123.

［9］李辉，郑海起，唐力伟，等.基于EEMD 和THT 的齿轮故障诊断方法［J］.振动、测试与诊断，2011，31(4):496-500.

LI Hui，ZHENG Haiqi，TANG Liwei，et al. Fault diagnosis of gear based on empirical mode decomposition and teager-huang transform［J］.Journal of Vibration Measurement and Diagnosis，2011，31(4):496-500.(in Chinese)

［10］朱宁辉，白晓民，董伟杰，等.基于EEMD 的谐波检测方法［J］.中国电机工程学报，2013，33(7):92-98.

ZHU Ninghui，BAI Xiaomin，DONG Weijie，et al. Harmonic detection method based on EEMD［J］. Proceedings of the CSEE，2013，33(7):92-98.(in Chinese)

［11］Maragos P，Schafe R W.Morphological filters-part I:their set theoretic analysis and relation to linear shift invariant filters［J］.IEEE Trans on Assp，1987，35(8):1153-1169.

［12］崔红芬，李鹏，王畅，等.基于数学形态学的微网电压补偿量检测方法［J］.中国电机工程学报，2013，33(16):122-128.

CUI Hongfen，LI Peng，WANG Chang，et al.A new detection method for microgrid voltage compensation based on mathematical morphology［J］.Proceedings of the CSEE，2013，33(16):122-128.(in Chinese)

［13］毛玲，孙即祥，张国敏，等.基于形态学运算和自适应阈值的心电信号消噪［J］.信号处理，2009，25(1):6-10.

MAO Ling，SUN Jixiang，ZHANG Guomin，et al.ECG signal de-noising based on morphological operations and adaptive threshold［J］.Signal Processing，2009，25(1):6-10.(in Chinese)

［14］章立军，杨德斌，徐金梧，等.基于数学形态滤波的齿轮故障特征提取方法［J］.机械工程学报，2007，43(2):71-75.

ZHANG Lijun，YANG Debin，XU Jinwu，et al. Approach to extracting gear fault feature based on mathematical morphological filtering［J］.Chinese Journal of Mechanical Engineering，2007，43(2):71-75.(in Chinese)

［15］石敏，吴正国，尹为民，等.基于RLS 算法的时变谐波检测［J］.电工技术学报，2005，20(1):50-53，82.

SHI Min，WU Zhengguo，YIN Weimin，et al.Time-varying harmonic detection based on RLS algorithm［J］.Transactions of China Electrotechnical Society，2005，20(1):50-53，82.(in Chinese)

［16］Case Western Reserve University.Case western reserve university bearing data center［EB/OL］.(2012-11-10)［2015-02-05］.http://csegroups.case.edu/bearingdatacenter/pages/download-data-file.