基于动态利率模型的利率衍生品定价分析

周闯洋

(浙江大学 经济学院，杭州 310027)

0 引言

利率衍生品是指价格依赖利率变动的金融产品，其价值主要依赖于利率变动。关于利率衍生品定价的核心问题在于如何计算利率的变动，而随机过程能够将利率的动态估算过程转变为现实，方便利率衍生品定价。利率衍生品是控制和管理利率风险的重要工具，有利于维护利率稳定，加快了我国利率市场化进程。因此，研究利率衍生品的定价具有一定的现实意义。

国内一些学者现在采用动态利率模型对利率衍生品进行定价预测常用的就是BDT模型，虽然BDT模型在利率衍生品定价过程中反映了动态性，但是该模型本身就对利率变动做了假设，即受单一期限的短期利率影响，这就难免使利率波动过程受到特征约束。基于此，笔者尝试构建新的动态利率模型，对利率衍生品的定价进行定量分析。本文主要在BDT模型的基础上，采用Hull和White（1993）的Hull-White模型，引入一种依赖于时间变化的参数变量，对利率衍生品进行定价分析。

1 动态利率模型的设计

1.1 BDT模型

BDT模型的先前假设条件是短期利率的波动情况随着时间的变化而发生变化，反映利率变化趋势的变量也受到当前利率水平的影响。于是，BDT模型具有反映利率期限结构瞬时波动特征的优势，其模型的思想为：设一组到期期限不尽相同的零利息国债的初始期限结构是给定的，即到期收益率和波动率给定，根据这些数值来测算未来短期利率的变动趋势。BDT模型还具有下列假设：任意债券价格的变动受单一期限的短期利率影响，且这个利率服从正态分布；任意债券的单期期望收益率相同；不存在交易费用；每一期利率的上升转移概率都是1/2。

根据上述假设，BDT模型表示如下：

其中，σ’表示后一期的短期利率r在瞬时的标准差；σ’/σ表示局部波动率，即短期利率的波动率随着时间的变动而发生变化；θ(t)表示由当期的无风险利率收益率决定的成分；dw则表示标准化后的正态随机扰动项。

BDT模型一般具有二叉树的结构特征，具体如图1所示。

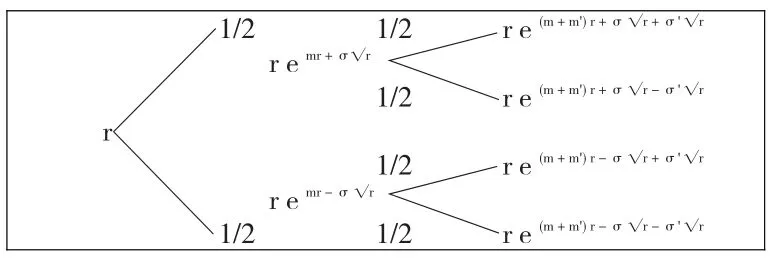
图1 BDT模型的二叉树结构

1.2 Hull-White模型

Hull和White于1993年提出了一种扩展的短期利率结构模型，通过引入一类动态性参数变量，使得模型对于利率波动性能够较好地反映出来。本文对该模型进行适当修正，主要思想是在短期利率模型的基础上引入一种依赖于时间的参数变量，使得模型具备均值回复的特征。如此，Hull-White模型便能够更好地对利率期限结构进行拟合。

Hull-White模型可表示如下：

其中，θ(t)表示均值的回复水平，由当期的无风险利率曲线所决定；α表示均值回复的速率大小，r(t)表示在t期的瞬时利率，dz表示标准化后的正态随机扰动项，σ表示波动率。根据式（2）可知，该模型的波动结构由均值的回复速率以及波动率两个变量决定，由此，利用该模型可以反映短期的利率波动结构特征。根据Hull和White的方法，可以得到债券价格的微分方程，从而得出期限为T的债券在t期的价格为：

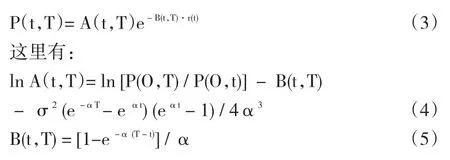
2 利率衍生品定价的实证分析

2.1 中国银行间市场和交易所市场国债定价的实证分析

首先，分别采用BDT模型和Hull-White模型对我国银行间和交易所市场的国债进行定价，然后通过对比定价结果，分析利率期限结构的选择情况。

（1）样本数据选取

首先，对当前的初始利率结构进行确定。考虑到当前国内债券市场的分离程度较高，银行间市场即便在衍生品品种和规模方面都有优势，但柜台交易方式受债券市场分离的约束，导致利率期限结构的数据存在失真可能。所以，本文将分别对银行间市场交易的国债和交易所市场交易的国债进行定价，而且利率期限结构的选择方面，采用相应债券分离出的利率期限结构。

本文从银行间市场和交易所市场2014年1月10日的债券中选择交易次数和交易数量较占优的10支债券作为目标债券，其中银行间与交易所市场各五支。根据BDT模型和Hull-White模型，对银行间市场国债定价选用银行间国债收益率曲线，对交易所市场国债定价选用交易所国债收益率曲线进行分析，具体数据见表1。

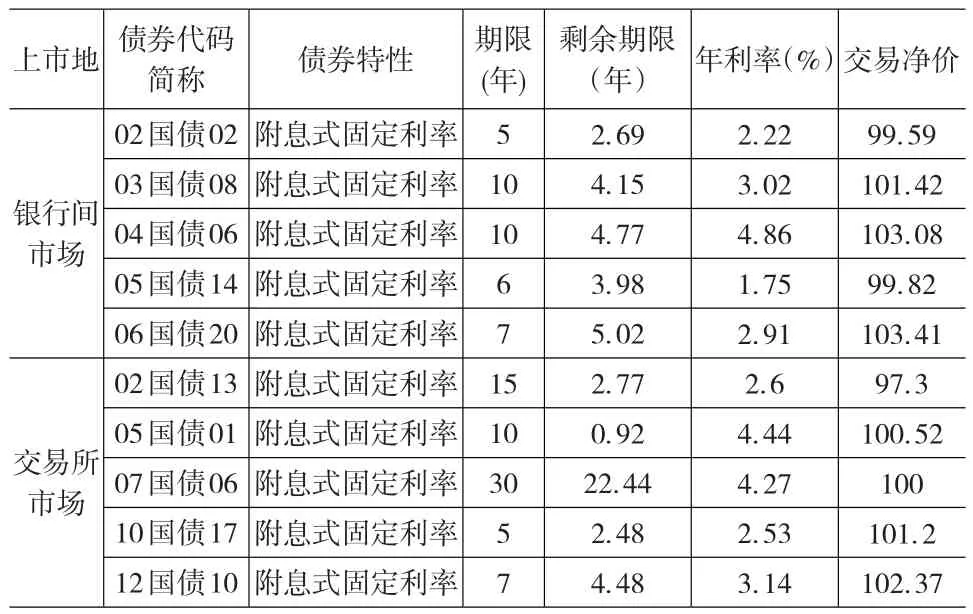
表1 银行间市场、交易所市场2014年1月10日定价目标债券

（2）模型参数设定

利用BDT模型与Hull-White模型进行参数设定，其中BDT模型需要确定与利率期限结构相匹配的收益波动率期限结构，而Hull-White模型的参数估计需要确定瞬时利率均值α回复变量及波动率σ。根据中国债券信息网及货币市场交易情况统计数据，7天回购利率在成交量以及参与率等方面都有一定得比较优势，且保持一定的动态特征。本文基于这一点，选择2014年1月1日以前的322个交易日的7天回购利率，同时排除未有交易的数据，最后得到298个数据。通过极大似然估计，得到BDT模型和Hull-White模型的参数设定结果如表2所示。

表2 BDT模型和Hull-White模型的参数设定结果

（3）利率三叉树的构造

在确定利率期限结构及相关参数后，利用Hull-White模型来构建利率三叉树。假定利率三叉树的时间间隔为Δt，利率间隔为Δr，节点(i,j)分别表示 t=iΔt和 r=r0+j Δr。一般情况下，当满足Δr=σ(3*Δt)1/2时，误差达到最小。通过分析可知，利率三叉树可能出现三种结构，具体的利率三叉树结构及相应的概率分布见图2。由于利率大小存在边界，不可能无限扩大，因此这里根据模型参数，设定j的上边界为0.168/(aΔt)。

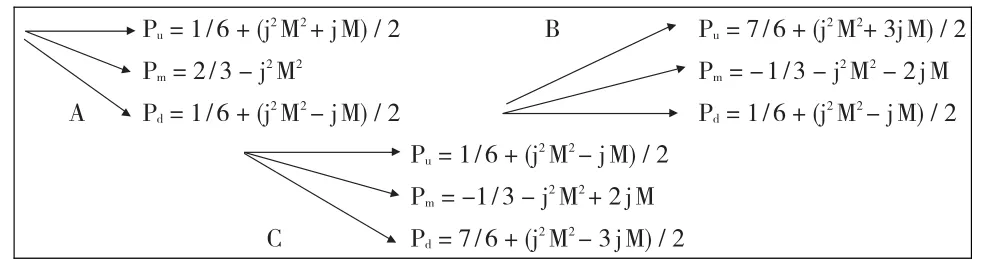
图2 Hull-White利率三叉树结构

（4）实证结果

根据以上数据及参数，分别采用BDT模型与Hull-White模型对银行间市场、交易所市场的5种债券进行定价估计，其中定价过程由Matlab 7.0编程计算，结果如表3所示。

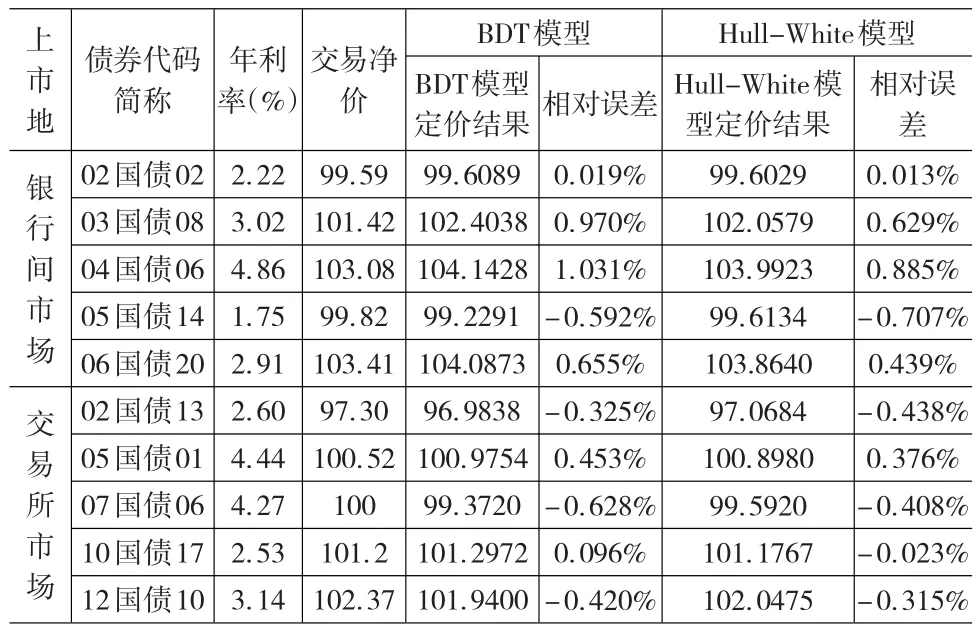
表3 银行间市场、交易所市场各5种债券的定价结果及相对误差

由表3结果可知，对于每一种债券而言，无论是采用BDT模型还是Hull-White模型，其最终定价估计结果的相对误差绝对值都低于2%。对比两个债券市场的结果可知，无论是哪种模型，银行间市场债券定价的相对误差总体上高于交易所市场。与此同时，采用BDT模型和Hull-White模型都能良好地实现国债的定价估计。对比BDT模型和Hull-White模型的估计结果又可发现，在10种债券中，有8种债券采用Hull-White模型的相对误差绝对值低于采用BDT模型的相应误差绝对值。由此笔者认为，总体上采用Hull-White模型对我国国债进行定价要优于BDT模型。比较两种模型的原理可以发现，Hull-White模型采用的是三叉树方法构建利率树，因此对瞬时利率的估计更为精准，而且Hull-White模型的均值回复速率仅取决于利率波动率，因此理论上Hull-White模型对利率衍生品的定价结果更为精确。

2.2 可回售债券定价的实证分析

可回售债券与利率波动具有密切关系，这种债券具有如下特征：当利率上升时，其价格将降低；当利率下降时，其价格将提高。近年来，国内经济进入“新常态”，经济增长速度放缓，投资后劲呈现不足，央行多次采取降低利率的措施以刺激经济。在这种情况下，市场上降息预期较大，回售债券的行为可能不热，由此可回售债券可能出现明显跌价。因此，本文采用Hull-White模型，对国内可回售债券进行定价，观察是否真的存在跌价现象。

仍采用三叉树方法进行估计。设PB为一般债券在某个树节点的价值，PP为可回售债券的价格，r为当期利率水平，C为在该节点处的选择权价值，X为债券回售的执行价。一般理性的可回售债券持有人将根据价值最大化原则进行定价，每个节点处可回售债券的回售权价值计算如下：

本文选取了2010年以来国家开发银行发行的5只可回售金融债券，分别是2010年第二十五期金融债券、2010年第三十四期金融债券、2011年第八期金融债券、2011年第五十二期金融债券、2011年五十五期金融债券，分别采用Hull-White模型进行定价估计。其中，模型参数的设定参照前面结果，5只可回售债券的定价估计结果如表5所示。

由表5可知，采用Hull-White模型进行定价估计，得

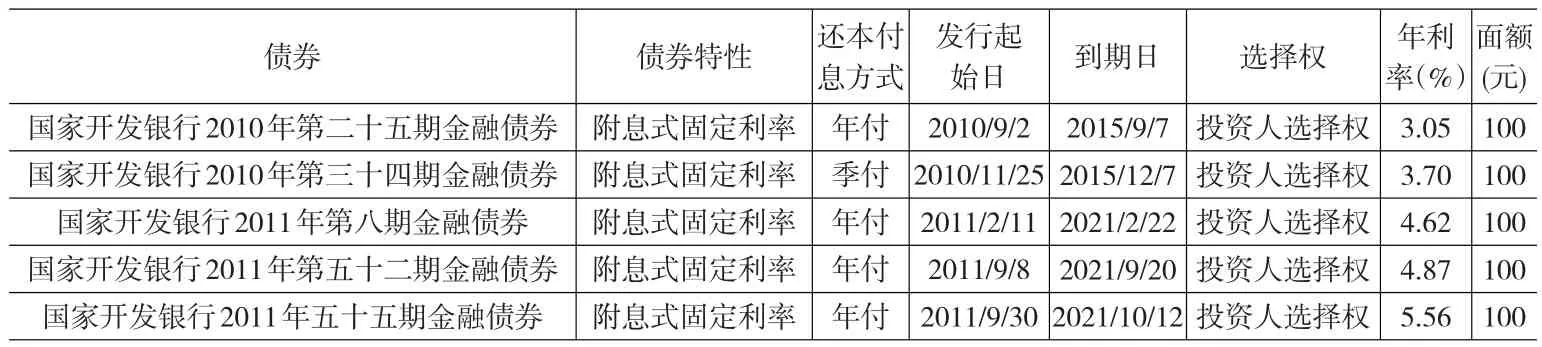
表4 国家开发银行5只可回售金融债券债券的基本数据

表5 国家开发银行5只可回售金融债券债券的定价结果

到的5只可回售债券的估计价格都非常接近100，即与原债券的发行面额基本相同。一方面，该结果验证了采用Hull-White模型进行定价估计的可靠性；另一方面也反映了近期国内债券市场发行的可回售债券的价格在一定程度上是趋于合理的。

3 结论

本文采用BDT模型和Hull-White模型，选取国内债券进行定价实证分析，从而研究债券这一利率衍生品的定价问题。由于BDT模型和Hull-White模型都是基于动态利率所构建的模型，因此都能体现利率的波动特性。

首先，通过对我国银行间市场和交易所市场的几只债券进行实证分析可知，银行间市场债券定价的相对误差波动总体上高于交易所市场，这体现了交易所市场债券定价的平稳性；同时，采用Hull-White模型对我国国债进行定价要优于BDT模型，这体现了Hull-White模型在债券定价方面的优越性。

其次，再次采用Hull-White模型对可回售债券定价进行实证，结果反映近期国内债券市场发行的可回售债券的价格在一定程度上是趋于合理的。即便近年来我国进入“新常态”，降息预期普遍存在，可回售债券跌价的可能性较大，但由于国内债券市场并不发达，市场参与度不高，因此“新常态”下国内可回售债券的跌价可能性仍然较小。

[1]Black F,Derman E,Toy W.A One-Factor Model of Interest Rates and Its Application to Treasury Bbond Options[J].Financial Analysts Journal,1990,(46).

[2]蒋承，郭黄斌，崔小勇.利率衍生品的定价研究——基于LIBOR市场模型[J].金融理论与实践，2010，（2）.

[3]冯奎.随机利率模型下的期权定价的实证分析[D].华中师范大学，2013.

[4]江良，林鸿熙.利率衍生品定价可行性模型[J].应用泛函分析学报，2014，（1）.

[5]续云丰，孔亚仙.利率模型综述及BDT模型在中债数据下的算法实现[J].绥化学院学报，2014，（9）.

[6]蒋春梅，郝晨.反射CEV模型与利率衍生品定价[J].南开大学学报（自然科学版），2014，（5）.

[7]Hull J A.White.One-Factor Interest Rate Models and The Valuation of Interest Rate Derivative Securities[J].Journal of Financial and Quantitative Analysis,1993,28(7).

[8]Chan K C,Karolyi,G A Longstaff F A et al.An Empirical Compari son of Alternative Models of the Short-Term Interest Rate[J].Journal of Finance,1992,(47).

[9]刘琳.关于企业债券的定价和利率风险的度量[D].南京：南京理工大学，2013.

[10]周荣喜，邱菀华.BDT模型的扩展及应用研究[J].数量经济技术经济研究，2005，（2）.

[11]Chen L.Stochastic Mean and Stochastic Volatility:A Three Factor Mo Del of The Term Structure of Interest Rates and Its Applications in Derivatives Pricing and Risk Management[J].Institutions and Instrument,1996,5(1).

[12]Heath D,Jarrow R A,Morton.A Bond Pricing and the Term Structure of Interest Rate A New Methodology for Contingent Claim Valuation[J].Econometrica-Wiley Online Library,1992,60(1).