探索规律,发展解决问题能力
朱辉
探索生活现象或数学现象中蕴含的规律,是数学学习的重要使命之一。因此,教学中要善于引导学生经历发现规律的过程,促进学生理解部分与整体的内在联系,通过有限去感悟无限,实现问题的有效解决。
一、联系生活,感知规律
探索规律是学生挑战自我的表现,也是展示学生才华与智慧的重要窗口。这是一个充满情趣与惊喜的探索之旅,学生能充分激活自己的知识积累、经验储备,进而积极地探索。探索数学现象中的规律,其间有困惑,也有喜悦,这是矛盾的载体,它会抓住学生的猎奇心理,诱发学生探究的好奇心,促使他们积极思考、乐于思考、敢于尝试。
如,在四年级上册“找规律”教学中,就以学生非常熟悉的情境为教学切入点:今天是星期几?明天呢?……通过司空见惯、极其熟悉的现象拉近规律与学生的距离,让学生感知到生活有规律,要善于研究和发现它们。利用学生的生活味原型,让学生在审视现实生活的同时,自发地感悟其中蕴藏的数学现象,从而激发学生学习数学的兴趣,使学生感受到数学与生活的密切联系。
再如,观察排列“□★○△□★○△…”,猜想其中蕴含的规律,想一想第9个是( )。学生把图形的规律弄清楚了,就很容易确定下一组图形。利用具体的图像提供的丰富表象,学生能够感知规律,并以规律作为判断的依据,顺利突破思维瓶颈,迅速解决问题。
二、活动反思,探究规律
巧妙地组织活动,引导学生对活动进行反思,探究规律,发现周期,利用周期的确定性去探求解决的方法。
如,在“找规律”的教学中,首先,设计站队活动游戏,让学生按照“男生、女生、男生……”这一规律排成一列;其次,利用人数增减的活动,引发学生思考“在变化中你发现了什么?”由于活动的主体是学生,学生会在站队中发现这种周而复始的规律。同时,在不同形式的变化中学生能够清晰地发现“开始男生,最后也是男生,男生一定比女生多1个”的规律,从而非常轻松地突破问题的难点。
再次,引入教材的主题图,引领学生进行观察,学生会自觉地把图中的信息进行梳理,也很直观地感悟到:夹子与手帕的关系、兔子与蘑菇的联系、篱笆与桩的关联性……图中的规律和站队活动的规律有机融合,实现学习的整合,促进知识的提炼和升华,学生能看出物与物之间的内在联系,悟出其中的周期性,从而能极其准确地把握规律。
三、灵活思索,发现规律
尽管生活现象、数学现象都纷繁复杂,但其中蕴含的规律是井然有序的。因此教师要促进学生从不同的角度去探索规律所在,让学生能够掌握其中的周期性,并进行科学合规的推理。例如,在具体的教学时组织画一画、想一想、算一算等自主学习活动,促使隐藏在现象中的规律逐步凸显出来,进而再现周期规律的合情推理活动。
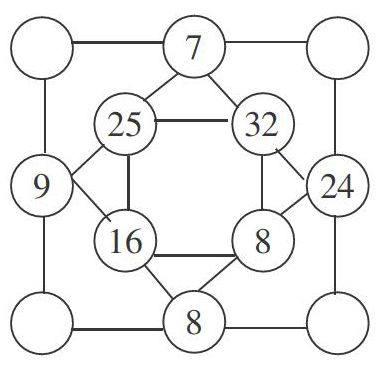
再如,在“教学100以内的加、减法”之后,组织竞赛游戏。先指导学生在最里面的小正方形的4个角中,任意地写出4个数;再组织学生计算出相邻两个数的差(大数减小数),并填在外围的正方形中;接着让学生自主探索规律……活动不仅能激发学生的探究兴趣,也让学生学会有序思考。当学生按照规律进行不断拓展时,他们一定会发现:最外边的正方形,四个角上的数最终都会变成0。
自主探索、小组合作,让发现规律变得简单轻松。学生在认真计算、分析后发现规律是那么的真实,从而充满了成就感。
四、内化知识,应用规律
探索规律的最终目的是应用知识,让其内化,达成学以致用的理想境界。所以在教学中教师不仅要努力创设适宜的情境,激活学生的认知积累,引领学生进行必要的探索研究活动,还要引导学生进行科学的归纳,使规律与数学知识学习更加紧密地结合,从而促进学生对新知的建构。
如,在“分数的基本性质”教学中,设计思考题 “一个分数的分子和分母都加上同一个数,这个新分数与原来的分数相比较,你认为符合分数的基本性质吗?为什么?”学生会举出不同的实例来验证该说法的不科学性,有的学生会在特殊的举例中获得结论:如果这个分数是等于1的假分数,那么这个规律是可以用的。学生的不同例证有效地拓宽了学习视角,学生会在分析研究中逐步明白,分数的基本性质只适用于分子和分母的倍数关系,而不适用于和差关系。同时,还可以引导学生去探究特例“2 / 3的分子加10,分母加上几,分数的大小不变?”使数学学习更具灵活性。
悟规律、找规律是探究学习的理想追求,教师要在这个过程促进学生通过归纳、类比获得猜想,进而推动学生加深对数学知识的理解进程,提升思考的层次。
(责编 童 夏)

