考虑侧向变形影响的路基沉降计算方法修正

陶 峰

（山西路桥集团 长临高速公路有限公司，山西 临汾 041000）

侧向位移作为评价路基稳定性的重要指标之一，路基侧向位移的过程往往伴随着沉降的发生[1-3]。然而目前路基沉降预测主要基于一维固结理论，其计算值与实际沉降值相差较大[4-5]。目前，学者们对路基侧向变形与沉降之间相互关系进行了一些针对性研究。张仪萍针对路基侧向变形引起沉降的特点，提出了一种包括时序自回归、线性加归和双线性的路基沉降预测模型[6]；王峰根据建立了客运专线路基有限元数值模型，分析了不同路堤高度和孔隙率对路堤沉降和侧向位移相互关系的影响[7]；杨武较全面地阐述了路基侧向变形对沉降影响的机理，并建立了数值模拟对分析路基侧向变形与沉降的相互关系[8]。但是，目前研究成果仅限于定性分析，且规范中沉降计算时仍定量未考虑侧向变形的影响。本文基于文献[8]数值模拟结果，提出了一种考虑侧向变形影响的路基沉降计算方法，为定量考虑侧向变形对路基沉降的影响提供参考。

1 研究思路

一维分层总和法中，压缩指数法（e-lgp）相对于其他分层总和法而言，有一个很大的改进之处：它和有限元法一样，都能够考虑土体应力历史对沉降的影响。因此，一般而言，沉降修正系数对于e-lgp法的修正效果要比对av法好，后者往往偏大。不过有限元法结果更精确、更接近实际，这是因为除此之外，有限元法还能考虑土体侧向变形对沉降的影响。针对不同的路堤填土高度和不同压缩性的天然土层，本文将提出不同的沉降修正系数，且可以对各亚层分别进行修正，与笼统地对分层总和法计算所得的最终沉降量进行修正有区别。

应用步骤：

a）确定路堤填土高度；

b）用常规方法对路基各层沉降进行计算，得出相应沉降Δs；

c）对各层沉降进行修正，得到各层修正沉降Δs；

d）将各层修正后的沉降量进行叠加求得最终沉降量S。

e）将修正后的沉降值与实测值或数值模拟结果进行对比，验证修正结果的可行性。

2 沉降计算

沉降修正系数φsl为有无侧向变形时路基压缩量之比，如式（1）：

建立文献[8]数值模型，路堤顶宽13.2 m，坡比为1∶1.5，填土高度为5 m，数值建模过程中路堤填筑分5层，每层1 m，逐层加载。地基计算深度30 m，计算宽度取4倍的路堤底部宽度，均由试算确定以保证有足够的精度。由于对称性，取半幅路基断面作为研究对象，如图1所示。土体参数如表1所示。给出沉降修正系数与填土高度和地基沉降之间的相互关系[9]如图2和图3所示。

由图2可以看出，随着路堤填土高度的增大，沉降修正系数逐渐增大，但增幅逐渐减小。泊松比μ越大，沉降修正系数越大，且随着泊松比μ的增大，沉降修正系数增幅逐渐增大。

收稿日期：2015－05－25；修回日期：2015－11－11

作者简介：陶 峰（1981— ），男，甘肃环县人，工程师，2009年毕业于太原理工大学土木工程专业。

图1 数值模型

表1 土体参数

图2 φsl与H的相关关系

在其他条件相同时，沉降修正系数会随深度的增加呈曲线变化：在地基深度范围内，修正系数先增大后减小，且修正系数峰值点出现深度与发生最大侧向位移的深度基本一致，在地基深度为5～10 m范围内，且填土高度降低，峰值点前移，如图3所示。

图3 沉降修正系数与深度的关系曲线

根据图2、图3进行非线性回归分析，可以得到沉降修正系数φsl与路堤填土高度H和路基土体泊松比μ的关系式如式（2）：

代入RH=H/L和孔隙比与泊松比之间的近似关系 e=5μ-0.75，其中L=13.2 m，则可得到关于 RH和孔隙比e的沉降修正系数φsl关系式如式（3）：

3 工程验证

某高速公路一典型剖面资料如下：路堤顶宽为26.0 m，坡比为1∶1.5，高度为5.5 m。路基中第1层土为灰黄色粉质黏土，埋深0～6.5 m；第2层为灰褐色粉质黏土，埋深6.5～22.8 m；第3层为黄褐色粉质黏土，埋深22.8～36.2 m。各层土埋深及其主要物理力学参数如表2所示。路堤填土主要指标为：重度为19.0 kN/m3；压 缩 系 数 为 0.36 MPa-1；孔 隙 比 为0.923。

表2 土层物理力学参数

由于路基中软土层不发育，故未采用地基处理措施。5.5 m高的路堤模拟现场施工进度可分为5次填筑，该路堤中心线与原地面交界处的实测沉降-时间-荷载曲线如图4所示，可见该路堤最终实测沉降约为32.5 cm。

图4 实测沉降-时间曲线

依据地质勘察资料，沉降计算深度取为35.0 m，再根据表2的各土层物理力学参数，分别用av法和e-lgp法进行沉降计算，可得沉降量分别为27.2 cm和26.4 cm。可见二者都比实测沉降量32.5 cm小，其中的一个重要原因就是这两种方法都没有考虑侧向变形所引起的附加沉降量。

对于上、下土层孔隙比相差不大的非均质路基，可以把各土层土体的厚度Ti作为权值，对它们的孔隙比求加权平均，把非均质路基转化为均质路基。根据表2，可得：

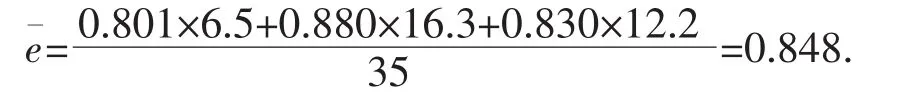
同时，RH=5.5/26.0=0.212，则由式（3）可得沉降修正系数：

分别根据文献[7-10]计算方法，可以得到3个不同的沉降修正系数1.135、1.146和1.203，将其与本文所得修正系数的修正结果进行对比分析，如表3所示，其中误差定义为：

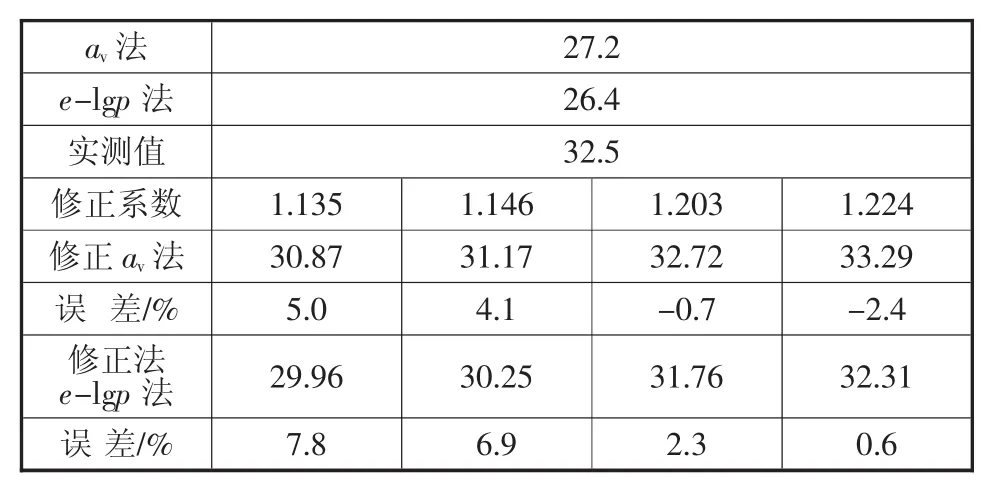
表3 根据不同修正公式所得修正结果的对比 m

由表3可知，利用本文所得修正公式对两种一维分层总和法计算所得结果进行修正后所得的结果非常接近实测值，特别是对于e-lgp法的修正结果，误差仅为0.6%。

4 结论

主要从引入考虑侧向变形的沉降修正系数着手，提出了一种考虑侧向变形影响的路基沉降计算方法，最后，通过工程实例进行分析，验证了该修正系数的可行性与合理性。得到以下结论：

a）随着路堤填土高度的增大，沉降修正系数逐渐增大，但增幅逐渐减小。泊松比μ越大，沉降修正系数越大，且随着泊松比μ的增大，沉降修正系数增幅逐渐增大。

b）在地基深度范围内，修正系数先增大后减小，且修正系数峰值点出现深度与发生最大侧向位移的深度基本一致。

c）对数值分析结果进行非线性回归分析，得到考虑侧向变形影响的沉降修正公式：φsl=（0.95+0.21RH）（1.08+0.178e）=1.224.，利用此公式对工程实例进行分析，可以减小计算结果与实测结果之间的误差。