粒子滤波在复合材料容器损伤中的应用
王舒婧
(1. 天津大学管理与经济学部;2. 一汽轿车销售有限公司)
声发射检测技术是近年发展起来的一种新型无损检测技术,材料结构的内部或局部在受力和受温度影响的状态下产生裂纹或塑性变形时,能量会快速释放,从而产生瞬态弹性波。声发射检测的主要目的是确定声发射源的位置和声发射发生的时间或载荷,分析声发射源的性质,并对其严重性进行评定。由于声发射探测到的能量来自被测试物体本身,因此,该方法可为延长设备使用寿命和增加可靠性提供新的途径[1]。
复合材料不同于钢制材料,它具有质量轻、抗爆、可监控及易制造且容器结构设计灵活等特点,应用非常广泛。但同时复合材料的非线性、受力复杂性和损伤形式多样性的特点使得对其进行检测比较困难。而声发射技术通过分析提取到的信号,可比较方便地对复合材料容器进行实时监控和随时复检,在复合材料容器损伤检测中有很广泛的应用前景。
1 声发射检测技术特点及应用
声发射检测是一种动态检验方法,声发射源主要是塑性变形、相变、亚临界裂纹扩展、压力泄漏、摩擦和磨损、裂纹面闭合与摩擦及撞击等。声发射检测方法的优点主要表现为[2~4]:
a. 声发射是一种动态检验方法,它能实时监视、检测运行中的设备和受力状况下的部件,由于探测到的能量来自被测试物体本身,并非外部提供,因此可以得到有关缺陷的信息。因采集到的压力容器声发射信号是由损伤发出的,故能较敏感的反映损伤随着外界条件的变化规律,具有很强的抗干扰能力。
b. 声发射检测方法对线性缺陷较为敏感,能够反映物质和结构的变化,探测到在外加结构应力下这些缺陷的活动情况,稳定的缺陷不产生声发射信号,检测灵敏度与分辨力高;设备早期故障阶段由于噪声的影响,声发射检测的AE信号能准确地提取损伤的有用信息。因此,针对压力容器的早期损伤的检测和预防,声发射检测比其他检测技术更加行之有效。
c. 可提供活性缺陷随载荷、时间及温度等外变量而变化的实时或连续信息,可以检测其他方法难以或者不能接近的环境或者形状复杂的被检件。
d. 声发射传感器可以检测多个方向的声发射信号,这使检测设备和程序简单化,同时也提高了检测设备微弱故障信号的效率。
e. 声发射信号的频率通常情况下高于振动信号。利用声发射技术采集压力容器损伤产生的AE信号时,在进行特征信息的提取时,能够有效抑制低频噪声的干扰。
声发射技术同样存在一定的缺点,如在静态缺陷的情况不能产生声发射现象。同时根据声发射的特点可以看出该技术对材料比较敏感,容易受到各种噪声的干扰。继金属压力容器之后,复合材料压力容器的检测才真正展开,借助复合材料明显的AE特征,利用声发射对其进行检测,具有可行性。
2 粒子滤波技术
滤波器方法是一种常用的状态估计故障诊断方法,对系统设备运转过程中产生的噪声和量测噪声没有任何限制,能够自适应地检测到声发射信号出现的异常状况。粒子滤波算法是20世纪90年代末发展起来的一种适用于非线性、非高斯系统的统计滤波算法,能够近似得到任意函数的数学期望并对系统的状态做出估计,但其计算量还是很大的。高斯为了测定行星运动轨道,在18世纪末就提出了最小二乘估计法,此后20世纪40年代Weiner和Kolmogorov相继独立的提出了维纳滤波理论[5~8]。粒子滤波(Particle Filter,PF)的思想基于蒙特卡洛方法(Monte Carlo Methods),它是利用粒子集来表示概率,可以用在任何形式的状态空间模型上。其核心思想是通过从后验概率中抽取的随机状态粒子来表达其分布,是一种顺序重要性采样法。粒子滤波技术在非线性、非高斯系统表现出来的优越性决定了它的应用范围非常广泛。
2.1算法介绍
用状态方程表示随时间变化的信息,与状态有关的噪声变量用量测方程描述,根据贝叶斯估计假设离散动态时变系统的状态空间模型为:
粒子滤波有预测和更新两种:
a. 预测。假设在k-1时刻,状态的后验概率分布p(x0:k-1|z1:k-1)是已知的,则状态的先验概率p(x0:k|z1:k-1)是由系统的状态转移概率p(x0:k|x0:k-1)推导出来的,即,p(x0:k|z1:k-1)=p(x0:k|x0:k-1)p(x0:k-1|z1:k-1)dx0:k-1。

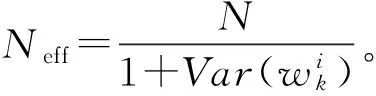
2.2粒子滤波算法步骤
粒子滤波算法(SIR)的本质就是将重采样算法引入到序贯重要性采样算法中,每迭代一次都要进行重采样,然后把似然函数作为重要性密度函数应用于SIS算法中,序贯重要性采样重采样粒子滤波算法的步骤如下:
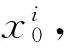


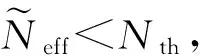

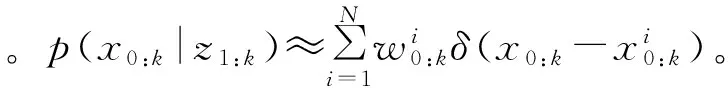
g. 状态估计。当k=k+1,出现新的观测值,进行步骤b。
粒子滤波算法流程如图1所示。
3 算例
笔者是以复合材料压力容器为研究对象,应用粒子滤波算法对其损伤行为进行研究。压力容器广泛应用于化工行业,由于损伤未能及时发现而引发的事故并不少见。为了提供较好的数据,需进行特征提取,把粒子滤波降噪方法应用到压力容器损伤的声发射信号处理中。
3.1声发射信号采集和提取
为了能够找到复合材料压力容器损伤声发射信号的特征频带,给以后的分析做准备,根据损伤声发射信号的特点和一些国际标准,设置信号采样参数为:设置需要的门槛,国标推荐使用53dB;前放增益为40dB;同时把模拟滤波器的下限频率设置为1.0kHz,上限频率设置为2.2MHz,根据采样原理,采样频率设置为3.0MHz;预触发51.2ms,长度2KByte。

图1 粒子滤波算法流程
利用小波变换对噪声信号进行提取,选用不同的小波对声发射信号进行不同层数的分解,自动生成阈值,并通过不同的小波重构系数对小波系数进行重构。
用ddencpm 函数自动生成阈值,将大于阈值的小波系数归零处理,小于阈值的小波系数保留下来,重构后都是噪声成分,最后得到的重构信号即为噪声信号,如图2所示。

图2 提取的声发射噪声信号
3.2粒子滤波的模型的建立
根据FPE 准则,通过Matlab编程,确定AR模型阶数。对其进行残差分析可知,确定模型阶数为4阶。故这组声发射数据的粒子滤波模型为:
xk=2.53xk-1-2.74xk-2+1.50xk-3-0.35xk-4+8.92×10-4
提取出噪声方差为0.004 2。
通过信噪比和均方根误差公式,利用Matlab 计算得出,粒子滤波消噪后的信号所提高的信噪比和均方根误差分别为14.91、0.03。
根据表1可知,均值、有效值、方差、峰值因子、峭度指标、波形因子、脉冲指标和裕度系数也都相应的有不同程度的降低,信噪比有了很大的提高,但是粒子数目多,导致计算量太大。

表1 复合材料压力容器声发射信号滤波前后参数对比
4 结束语
笔者以复合材料压力容器为研究对象,通过粒子滤波算法,对复合材料压力容器损伤的声发射信号进行分析。首先从粒子滤波的理论出发,确定粒子滤波的状态方程系数,运用FPI准则进行声发射信号AR模型阶数的确定,建立粒子滤波模型;最后进行消噪,提高信噪比。
[1] 李孟源,尚振东,蔡海潮,等.声发射检测及信号处
理[M].北京:科技出版社, 2010:148.
[2] 杨杰.声发射信号处理与分析技术的研究[D].吉林:吉林大学,2009.
[3] 陈玉华,刘时风,耿荣生,等.声发射信号的谱分析和相关分析[J].无损检测,2010,24(9):395~399.
[4] 胡昌洋,杨钢锋,黄振峰,等.声发射技术及其在检测中的应用[J].计量与测试技术,2008,35(6):1~2.
[5] 谢朝阳.声发射信号处理方法分析[J].中国科技信息,2009,(5):131~132.
[6] 徐春雷.基于粒子滤波方法的齿轮箱故障诊断技术[D].太原:中北大学,2013.
[7] 许听.基于滤波技术和粒子群优化的齿轮箱故障诊断研究[D]. 太原:中北大学,2011.
[8] 马航.齿轮箱的故障诊断中粒子滤波技术的应用[D].太原:中北大学,2011.

