永磁同步电动机单闭环位置伺服系统设计

吕永健，杨 铭

(空军工程大学，西安710038)

0 引 言

常见的电机位置伺服系统是在速度伺服系统的基础上，通过增加位置环来实现对电机角位移的控制。目前三环结构是传统位置伺服系统最常见的结构形式，在每个控制环上都需要相应的调节器来使被控制量跟踪参考值。目前调节器最常见的控制算法为PID 控制器。这种控制方式不需要控制对象的输入输出模型信息，仅需要实际值与给定值之间的误差，原理结构简单。但随着控制对象多样化，对系统动静态品质要求不断提高，PID 控制方式的缺点逐渐显现。当被控对象的工作状态多变，运行环境较复杂时，若采用三环PID 控制器，一方面三个PID参数调节困难，适用范围较小;另一方面系统抗扰能力差，外界非常值扰动很容易影响系统伺服精度［1］。自抗扰控制技术在PID 控制思想的基础上，通过实时估计补偿外扰增强系统抗扰性，改善系统动静态性能，目前自抗扰控制器(以下简称ADRC)已被广泛应用于电机控制中［2－4］，但这些研究仅以ADRC 作为单个闭环上的调节器，系统总体仍保持多环结构，这样并没有完全发挥ADRC 的优势，而且还大大增加了系统软件结构的复杂程度。

针对上述问题，本文设计了基于自抗扰控制器的永磁同步电动机单闭环位置伺服系统。该系统采用直接转矩控制理论，并通过空间电压矢量调制法降低系统的转矩脉动，实验证明该系统具备良好的动静态性能及较强的抗扰性。

1 单环自抗扰控制器可行性分析

ADRC 控制器是在PID 框架的基础上通过扩张状态观测器(以下简称ESO)对系统的未知外扰进行观测并补偿，从而提高系统的动静态性能及抗扰性。以二阶系统为例，其基本原理如下:

对于二阶系统:

式中:x1，x2为可观测状态量;y 为输出量;N(t)为外部扰动总和;f(x1，x2，…xn，t)为各状态量耦合而成的时变非线性函数;u(t)为控制输入量;b0为控制量比例系数。取α(t)为扰动总和，有:

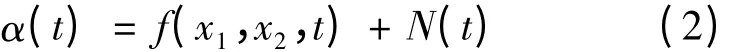
设计三阶ESO:

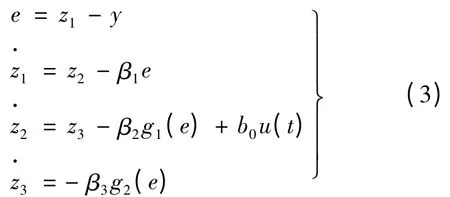
式中:x1，x2观测值为z1，z2;g1(e)，g2(e)代表关于e的函数表达式。通过选择合适的g1(e)，g2(e)函数形式及比例系数β1，β2，β3，就能使ESO 跟踪系统各状态量并通过扩张状态z3估计系统扰动总和α(t)。跟踪微分器(TD)能够跟踪目标信号v 并给出其微分v2，与ESO 输出的z1，z2比较后送入NLSEF 得到系统输入控制量为u0。根据ESO 的观测结果构造新的输入控制量u，有:

这样就可以通过u 补偿α(t)的影响使式(1)变成积分串联型系统。

永磁同步电动机的DTC 理论基础［6－7］如下:

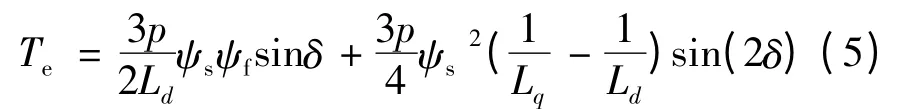
式中:ψs，ψf分别为定、转子磁链幅值;p 为转子极对数;δ 为二者夹角，称为转矩角。由式(1)可知，在一定范围内Te随δ 单调递增，因此通过控制δ 角便可实现对Te的控制。

永磁同步电动机机械转速ωr表达式:

将式(6)代入式(5)，有:

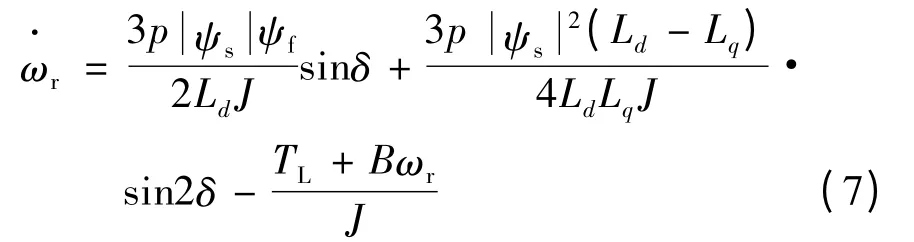
sinδ 的一阶泰勒级数展开式:

取u=δ，b0，α(t)如下:

则式(7)变为:

综上，从理论上讲，ADRC 完全能够实现对α(t)的估计与补偿，通过调节电机角加速度进而实现位置伺服。同时，由于三阶ESO 能够给出角位移、较速度、角加速度三种信号，只需单闭环便可实现对位置伺服系统的控制。

2 单环位置伺服系统设计

本文设计的永磁同步电动机位置伺服系统的基本结构如图1 所示，它主要包括控制器、状态量检测与估计、驱动脉冲生成、硬件系统(逆变器与电机)等四个部分。该系统直接将ADRC 输出量u 作为永磁同步电动机的期望转矩角δ*，经运算后得到参考电压矢量Uref送入SVM 环节进行调制。图中ψs，分别为实际、期望定子磁链矢量;us，is为定子电压，电流合矢量;Rs为定子电阻;Ts为SVM 算法的控制周期，θr分别为期望、实际机械角位移;为B，C 相定子相电流值。

图1 基于单闭环SVM-DTC 控制系统结构图

2.1 自抗扰控制器设计

设计三阶ESO:

式(12)中fal 的函数形式:

采用文献［1］中的离散最速控制综合函数fhan构造跟踪微分器(TD)来安排过渡过程。考虑由ESO 生成的补偿控制量可完全抵消包括负载转矩TL在内的系统扰动影响，因此不需要误差积分环节的作用。取非线性状态误差反馈(NLSEF):

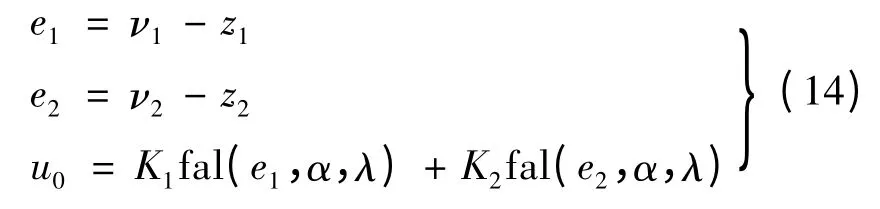
式(13)、式(14)中，ν1，ν2为机械角位移指令的跟踪信号与微分信号;α;α1，α2，λ 可按文献［1］方法给出;β1，β2，β3比较容易整定，因此需要调节的参数只有K1，K2。

2.2 磁链误差Δψs 与参考电压Uref计算

将u 作为期望转矩角δ*，进而可到期望定子磁链ψ*

s 在两相静止坐标系(α－β 坐标系)中的位置。图2 为ψs与ψ*s 的关系示意图。图中δ 为当前实际转矩角，θe为d 轴相对于α 轴的电角度。

图2 永磁同步电动机空间矢量关系示意图

定子磁链观测器采用一阶惯性滤波积分器［8］。根据图2 有:

在α－β 坐标系中计算Δψs:

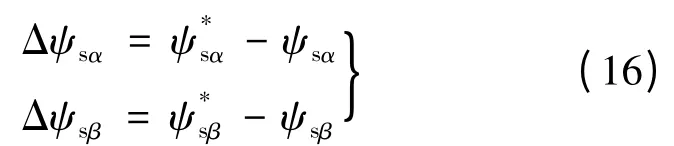
在计算Uref时应考虑到定子电阻Rs影响，有:

2.3 SVM 模块设计

为与仿真软件中坐标定义相符，令β 轴与定子绕组A 相重合，α 轴滞后β 轴90°，建立两相静止坐标系，各电压矢量及扇区标号如图3 所示。

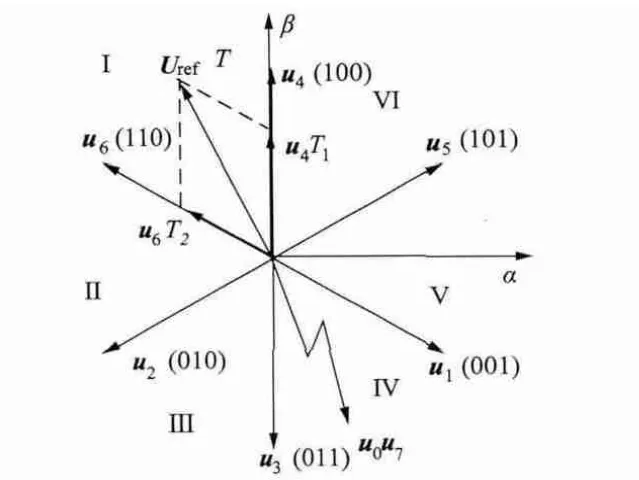
图3 SVM 原理示意图

图中，u1～u6为逆变器输出的基本电压矢量(运动电压矢量)，u0，u7为零矢量。设直流母线电压为2Udc，I ～VI 为基本电压矢量分割的六个扇区的编号，三位二进制码代表逆变器ABC 三相，1 代表上桥臂开通下桥臂关断，0 相反。

(1)Uref所在扇区判断

x≥0 时sig(x)=1，x ＜0 时sig(x)=0。由上式可得N 与扇区号的对应关系如表1 所示。

表1 扇区号与N 对应关系

(2)电压矢量作用时间计算

Uref由相邻的两个基本电压矢量合成，以扇区I为例，设u4，u6作用时间分别为T1，T2，有:

表2 各扇区基本电压矢量作用时间表

若T1+T2≤Ts，则周期内剩余时间由零矢量填补，作用时间为T0=Ts－T1－T2。若T1+T2＞Ts，令:T1=T1Ts/(T1+T2)，T2=T2Ts/(T1+T2)。

(3)三相桥臂切换时间计算

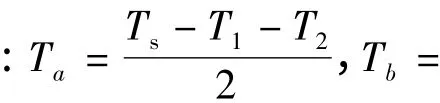
表3 三相桥臂开关时刻表

3 系统仿真验证

关于ADRC 仿真参数设置，根据文献［1］一般取为如下值:δ =0.01，α1=0.5，α2=0.25。ESO 参数β1，β2，β3满足如下关系［1］:

式中:x 的值根据永磁同步电动机的最大输出转矩而定。这样三个可调参数转化为一个，经过仿真发现，当x =0.000 2 时，ESO 能够跟踪系统各状态量的变化，并能准确描述扩张状态量z3的变化，此时β1=5 000，β2=220 970，β3=1 596 449。由于系统实现的是位置伺服，角位移误差反馈所占比重应相对较大，故设置NLSEF 环节中K1=0.9，K2=0.5，α=0.75。

为模拟永磁同步电动机实际运行环境，在给永磁同步电动机输入阶跃负载信号的同时，混入在［－0.5，0.5］区间内随机分布步长1 ms 的噪声信号作为干扰，得到的电机输入负载转矩波形如图4所示。

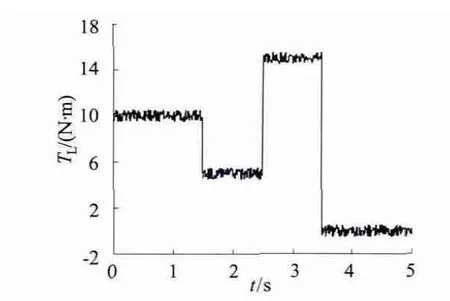
图4 负载转矩变化波形

伺服系统其它参数设置:Udc=155V，Rs=1Ω，p =4，ψf=0.42Wb，Ld=12.765mH，Lq=7.695mH，J =0.005 kg·m2，B=0.0001 N，给定ψ*s =0.6 Wb，Ts=80 μs，限制起动转矩33.5 N·m。当给定角位移θ*

r =50 rad 时，系统的角位移响应及其局部放大图如图5 所示。由图5 可见，在受到负载突变干扰时，系统能够较快速地恢复到给定值，同时能够抑制非定常扰动的影响，使系统角位移较好跟踪位置指令，表现出良好的抗扰性。

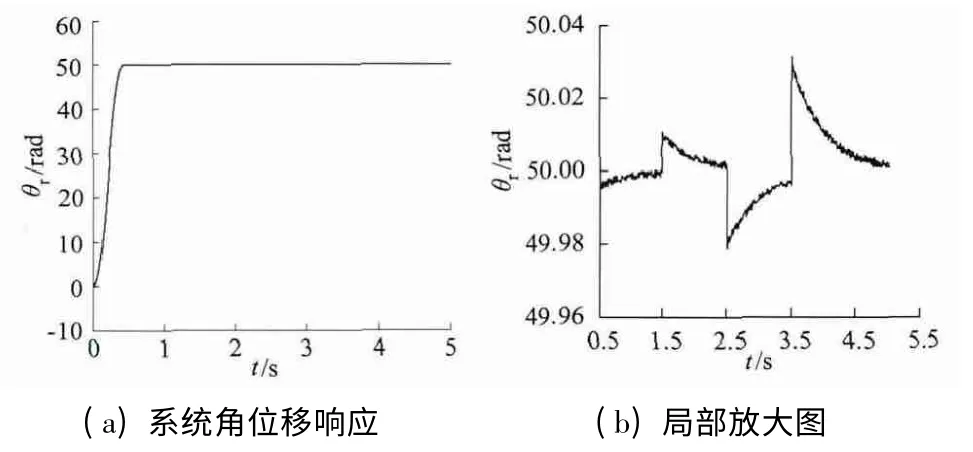
图5 稳态角位移响应及其局部放大图

图6、图7 分别为系统转矩响应曲线与ADRC中ESO 对扩张状态量α(t)的观测结果z3。对比图4 与图6 可以看出，ADRC 通过z3实现了对系统扰动的补偿，Te变化基本与TL保持一致。

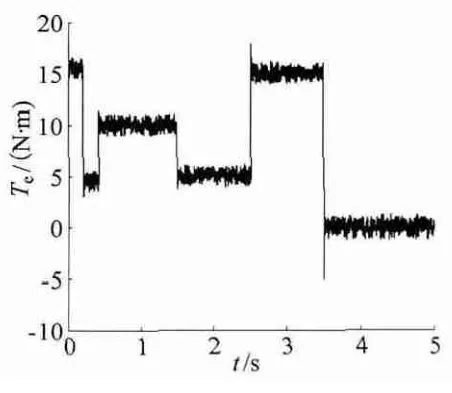
图6 系统的转矩响应

图7 扩张状态量z3 观测结果

为对比分析，另搭建了三环位置伺服系统模型，位置环采用自抗扰控制器，转速、转矩环均采用PI控制器，在转速均无超调的情况下三环、单环部分指标对比如表4 所示。由表4 数据可见，在对系统结构进行简化后，单闭环仍能够达到三环的控制效果，部分指标甚至优于双环系统。证明了单闭环替代三环系统的可行性。

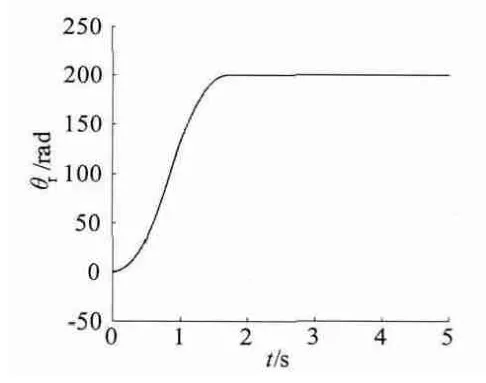
图8 =200 rad 系统角位移响应

图9 =5 rad 系统角位移响应

表4 单、三环系统性能指标对比

4 结 语

本文设计的基于ADRC 单环SVM－DTC 永磁同步电动机位置伺服系统，能够保证良好的动静态性能，且具有良好的鲁棒性。同时相对与传统的三环控制系统而言，结构大大简化，且参数整定更为简洁，能够在位置指令较大变化范围内保持良好的参数适应性。综上所述，本文设计的单环位置伺服系统能够替代传统三环系统，具有较强的应用价值。

［1］ 韩京清.自抗扰控制技术［M］.北京:国防工业出版社，2008.

［2］ 刘英培，万健如，梁鹏飞.基于扩展卡尔曼滤波器和电压空间矢量调制的永磁同步电机直接转矩控制［J］.中国电机工程学报，2009，29(27):67－74.

［3］ 刘子建，吴敏，王春生，等.基于自适应观测器和自抗扰控制的PMSM 直接转矩控制［J］. 系统仿真学报，2010，22(11):2702－2707.

［4］ 刘英培.基于自抗扰控制PMSM 电压空间矢量调制直接转矩控制方法［J］.电力设备自动化，2011，31(11):78－82.

［5］ 邱鑫，黄文新，杨建飞，等.一种基于转矩角的永磁同步电机直接转矩控制［J］.电工技术学报，2013，28(3):56－62.

［6］ 周扬忠，胡育文.交流电动机直接转矩控制［M］. 北京:机械工业出版社，2009.

［7］ ZHONG L，RAHMAN M F，HU Y W，et al. Analysis of direct torque control in permanent magnet synchronous motor drives［J］.IEEE Transaction on Power Electronics，1997，12(3):528－535.

［8］ 李崇坚.交流同步电机调速系统［M］.北京:科学技术出版社，2006.