无刷直流电动机直接转矩控制零矢量分析研究

杨建飞，胡育文，刘 建，邱 鑫，吴华仁，钱伟行，郭爱琴

(1.南京师范大学，南京210042;2.南京航空航天大学，南京210016)

0 引 言

无刷直流电动机(以下简称BLDCM)因其结构简单、价格低廉、调速性能良好等特点，在众多领域得到了广泛应用［1］。但由于反电势和供电电流非正弦，存在换相转矩脉动等原因，导致电机运行过程中转矩脉动较大，限制了其进一步的应用。而直接转矩控制方法(以下简称DTC)由于将电机和逆变器作为一个整体，直接以电机转矩作为控制对象，受系统参数影响较少，能够有效降低转矩脉动，备受国内外学者青睐［2－3］。在正弦波永磁同步电机DTC方法中，由于在一个控制周期内只发出一个电压矢量，导致电机的转矩脉动比较大，而在引入零电压矢量后则能够显著降低转矩脉动［4－5］，因此，如何在BLDCM DTC 系统中定义合适的零电压矢量就成为了该系统研究中需要解决的一个关键问题。文献［6－7］在首次提出的直接转矩控制系统中定义逆变器开关管全关对应的电压矢量为零矢量，并首次实现了BLDCM 的直接转矩控制，很多学者在此后的研究中采用了文献［6］所定义的零电压矢量［8－9］，同时结合占空比控制等方法来降低转矩脉动［10－11］。

本文在详细分析了BLDCM DTC 中全关零矢量作用条件下电机电流，电压变化规律的基础上，根据两相120°导通的特殊控制要求，提出了一种适用于该控制系统的新的零矢量，不同电压矢量在不同运行条件下的对比仿真结果验证了所提出的新的零矢量的正确性以及降低转矩脉动的有效性。

1 BLDCM DTC 系统中零矢量的分析

1.1 BLDCM 纯转矩环DTC 系统分析

对于定子采用三相星型、无中线连接的BLDCM，其与电压型逆变器等效电路图如图1 所示。其中，ua，ub，uc为定子三相相电压;ia，ib，ic为定子三相相电流;ea，eb，ec为定子三相相反电势;Rs，L 为定子每相电阻与等效电感;UDC为直流母线电压。

由于BLDCM 的气隙磁场、反电势以及稳态电流均为非正弦波，因此常用电机的相变量来建立其模型，其电压方程如下:

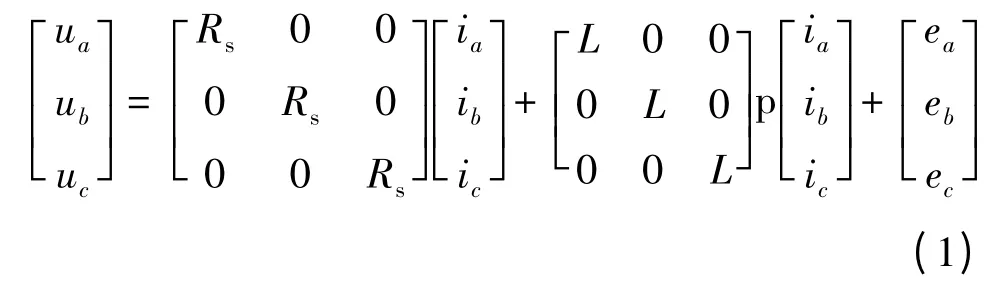
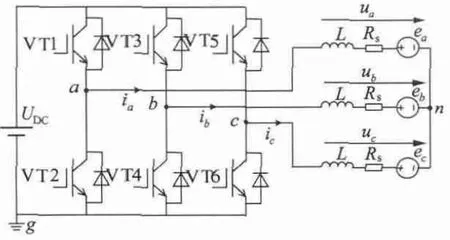
图1 BLDCM 与逆变器等效电路图

转矩方程如下:

式中:Ωr为转子机械角速度;Te为电机转矩。

在纯转矩环DTC 系统中，控制系统根据电机转子位置所处的扇区同时结合转矩控制要求，选择合适的电压矢量作用于电机，以实现对转矩的直接控制。由于电机运行过程中同一时刻仅有两相导通，结合图1 可以得到导通相相电压合成矢量分布，如图2 所示。由于存在关断相，采用六个二进制数来表示图2 中每个电压矢量对应的开关管状态，以V1矢量为例，其从左至右的二进制数值分别表示图1中对应的1 ～6 开关管的状态，“1”表示导通，“0”表示关断。

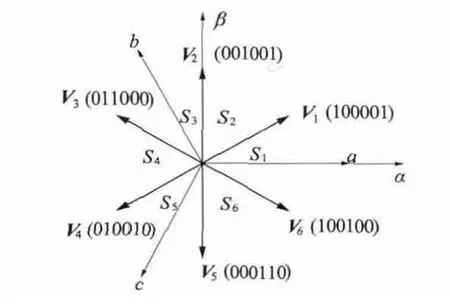
图2 导通相相电压合成矢量

在图2 的扇区划分的基础上，根据表1 选择电压矢量，以实现对电机转矩的直接控制，其中τ 为转矩控制标志，“1”为增加转矩，“0”为保持转矩，“－1”为减小转矩。其中，当需要保持电机转矩时，选择V0矢量，并且定义开关管全关对应的电压矢量为V0矢量。

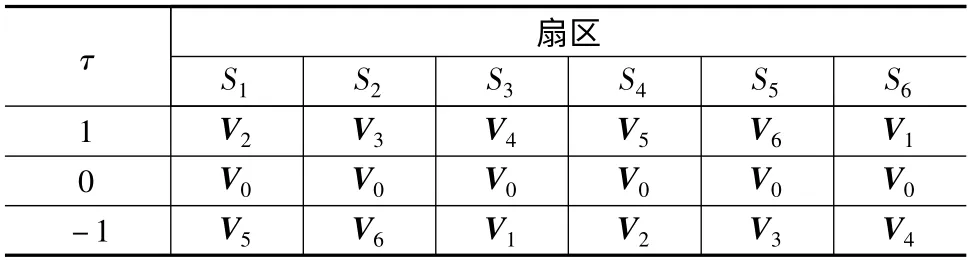
表1 纯转矩环DTC 电压矢量选择表

1.2 全关零矢量作用分析

在由电压型逆变器和电机构成的调速系统中，一般定义电机中综合电压矢量等于零的空间电压矢量为“零矢量”。在异步电动机和正弦波永磁同步电动机DTC 系统中，综合电压矢量等于零即意味着电机三个端点短路，可通过控制图1 的逆变器三个桥臂上管均导通或下管均导通来实现，而在两相导通BLDCM DTC 中，纯转矩环控制方法是通过控制六个开关管全关来实现的。下面首先分析一下全关零矢量作用条件下电机端电压和电流的变化规律。

以a 相关断，b 相与c 相导通，且电流从b 相流入c 相流出为例(导通状态如图3(a)所示)，此时VT3 管、VT6 管导通，VT1、VT2、VT4、VT5 管均关断，电流流向如图3(a)箭头所示，作用在电机上的电压矢量为V2。此时若选择全关零矢量也即将6 个开关管全关，由于电机电感中的电流不能突变，电流流向变成如图3(b)所示，VT4、VT5 管的续流二极管被迫导通，作用效果和VT4、VT5 开关管导通的效果等价，而VT4、VT5 开关管导通所对应的电压矢量V5正是VT3、VT6 管导通形成的电压矢量V2的反矢量。在其他条件下选择全关零矢量的作用效果类似，因此，两相导通BLDCM DTC 系统电流连续条件下，选择全关零矢量作用于电机后，在电机中没有形成所需要的“零矢量”，而是形成了原电压矢量的反矢量，这违背了DTC 系统中选择零矢量的初衷，不符合DTC 对转矩的控制要求，因此，有必要重新研究两相导通BLDCM DTC 系统中正确的零矢量。

图3 全关零矢量作用前后电流流向

1.3 新零矢量定义分析

要实现真正的零矢量作用于电机，则要控制电机两导通相的端点短路。仍然以图3(a)的导通情况为例，在此条件下使电机两导通相端点短路的方式有两种:导通相桥臂上两管导通或下两管导通，分别对应的零电压矢量为(001010)和(000101)，相应的等效电路分别如图4(a)和图4(b)所示。

图4 不同零矢量作用下电流流向

从图4 中可知，在两个新的零电压矢量作用下导通相b 相与c 相的端点均被短路，满足零电压矢量的形成要求。进一步的，虽然上述分析是在V2矢量作用下进行，但这两个零矢量同样适用于V5矢量作用时的情况。当选择其他电压矢量作用时，可依此确定相应的零电压矢量。在表1 的基础上整理得到表2 的适用于不同扇区的零电压矢量选择表。

表2 两相导通BLDCM DTC 系统中零电压矢量选择表

从表2 可知，适用于两相导通BLDCM DTC 系统的零矢量共有6 个，用变量Vxy表示，下标x 表示开关管导通情况:7 表示上桥臂两个开关管开通，下桥臂两个开关管关断对应的零矢量，0 表示上桥臂两个开关管关断，下桥臂两个开关管开通对应的零矢量。下标y 表示对应的扇区，由于S4，S5，S6扇区和S1，S2，S3扇区的零矢量一样，因此共用S1，S2，S3扇区的零矢量。本文将六个非零电压矢量V1，V2，V3，V4，V5，V6和六个零矢量V71，V72，V73，V01，V02，V03定义为两相导通BLDCM DTC 系统中的电压矢量集合。在单环两相导通BLDCM DTC 系统中，根据表1 选择合适的电压矢量，当需要保持电机转矩时根据表2 选择新定义的零矢量作用于电机，以降低转矩脉动。

2 不同电压矢量作用下仿真对比

为了验证理论分析的正确性和所提零矢量的有效性，利用MATLAB 软件分别建立不同电压矢量作用条件下的仿真模型。电机参数如表3 所示。

表3 BLDCM 电机参数

2.1 全关零矢量作用条件下对比仿真

为了验证全关零矢量作用效果，根据表1，分别进行只有正矢量和反矢量以及只有正矢量和全关零矢量作用条件下的对比仿真。仿真中控制周期60 μs，给定转速200 r/min，负载转矩1.2 N·m，两种控制方法下转矩波形如图5 所示。

图5 全关零矢量作用下转矩对比仿真波形

从图5 可知，当分别采用正/反矢量和正/全关零矢量时，二者转矩脉动分别为1. 171 N·m 和1.173 N·m，两种条件下的转矩脉动非常接近。将控制周期内电机转矩随不同电压矢量的变化示于图6 中，其中电压矢量序号和图2 中的电压矢量下标对应，“0”表示选择全关零矢量。

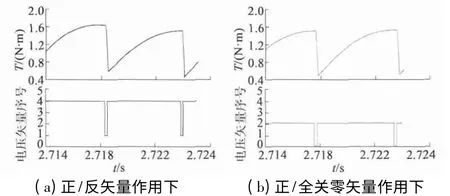
图6 控制周期内全关零矢量作用下转矩变化仿真波形

从图6 可知，两种控制方法下控制周期内转矩的增加量均显著小于转矩的减小量，初步说明全关零矢量对转矩具有较强的减小作用，将图6 中控制周期内的转矩变化量进行整理，如表4 所示。

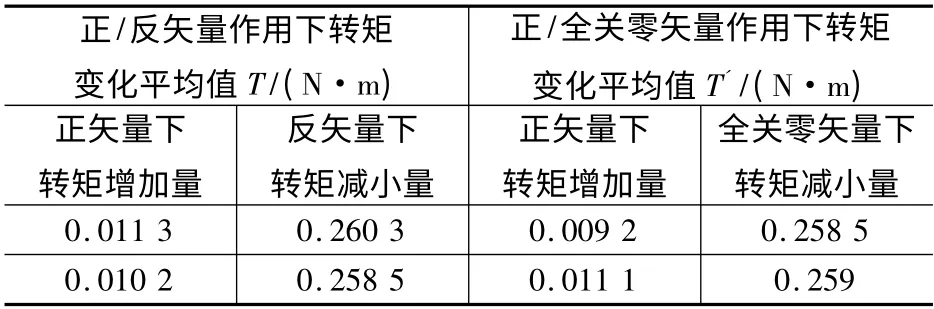
表4 不同控制方法下控制周期内转矩变化量

从表4 中可知，两种控制方法下正矢量对转矩的增加量均要明显小于反矢量和全关零矢量，这和正弦波永磁同步电动机DTC 中的作用规律类似，而反矢量和全关零矢量分别作用时控制周期内的转矩变化量非常接近，说明全关零矢量对转矩的控制作用和反矢量等效。为了进一步说明全关零矢量作用条件下电机端电压和电流的变化情况，将电机端电压和电流变化情况示于图7 中，考虑到母线电压和相电流数值上的差异，为便于分析，将端电压进行了标幺化，基值为母线电压36 V。

图7 全关零矢量作用下端电压和电流波形

从图7 的端电压和电流波形可知，当选择全关零矢量时，导通相端电压均发生变化，所形成的是原有电压矢量的反矢量。以图7 中标注时刻为例，当选择全关零矢量时，前一矢量选择的是V1，对应于VT1 和VT6 开关管导通，导通相为a 和c 相，对应端电压分别为36 V 和0，施加全关零矢量后，由于导通相电流连续不能突变，此时VT2 和VT5 开关管对应的续流二极管导通，导通相端电压变为0 和36 V，效果等同于电压矢量对应的反矢量V4，和理论分析结果一致，与表4 中控制周期内反矢量和全关零矢量分别作用下的转矩变化结果吻合，因此，全关零矢量在电流连续条件下对电机转矩的控制效果和相应的反矢量等效，传统控制方法中所采用的全关零矢量并不是真正意义上的零矢量。

2.2 新零矢量作用条件下的仿真

为了验证所提出的新零矢量对转矩脉动抑制效果的有效性，将表1 中全关零矢量换成表2 中新定义的零矢量，也即当需要保持电机转矩时选择新定义的零矢量作用于电机。电机仿真条件和前面相同，零矢量作用范围为0.25 N·m。电机转矩波形如图8 所示。

从图8 可知，在引入新定义的零矢量后电机转矩脉动降为0.72 N·m，初步显示了新零矢量抑制转矩脉动的有效性。将控制周期内新零矢量作用条件下的转矩变化情况示于图9 中。

从图9 中可知，控制周期内新零矢量作用下电机转矩的减小量要显著小于反矢量，图9 的仿真波形中新零矢量作用下电机转矩减小量分别为0.133 8 N·m 和0.127 8 N·m，均显著小于全关零矢量和反矢量作用下的转矩减小量。因此，在电机稳定运行过程中，当需要保持电机转矩时，通过选择新提出的零矢量代替传统控制方法中的全关零矢量可以有效降低转矩脉动。

3 结 语

两相导通BLDCM DTC 纯转矩环控制系统中将零矢量定义为开关管全关对应的电压矢量导致导通相电流作用在电机上的本质上为其相应的反矢量。本文根据两相导通BLDCM 运行过程中电压电流的特点，从零矢量本质定义出发，提出了一种适用于该系统的新的零矢量，仿真结果验证了理论分析的正确性以及新零矢量对转矩脉动抑制作用的有效性，有助于进一步完善两相导通BLDCM DTC 系统理论体系。

［1］ KENJO T，NAGAMOTI S.Brushless motors:advanced theory and modern applications［M］. Tokyo，Japan:Sogo Electronics Press，2003.

［2］ TAKAHASHI I，NOGUCHI T.A new quick－response and highefficiency control strategy of an induction motor［J］.IEEE Transaction on Industry Applications，1986，22(5):820－827.

［3］ ZHONG L，RAHMAN M F，HU Y W，et al. Analysis of direct torque control in permanent magnet synchronous motor drives［J］.IEEE Transaction on Power Electronics，1997，12(3):528－535.［4］ HU Yuwen，TIAN Cun，GU Yikang，et al. In－depth research on direct torque control of permanent magnet synchronous motor［C］//IEEE 2002 28th Annual Conference of the Industrial Electronics Society.Seville，Spain，2002:1060－1065.

［5］ 孙丹，贺益康.基于恒定开关频率空间矢量调制的永磁同步电机直接转矩控制［J］.中国电机工程学报，2005，25(12):112－116.

［6］ LIU Yong，ZHU Z Q，HOWE D. Direct torque control ofbrushless DC drives with reduced torque ripple［J］.IEEE Trans. on Industry Applications，2005，41(2):599－608.

［7］ LIU Yong，ZHU Z Q，HOWE D. Commutation－torquerippleminimization in direct－torque－controlled PM brushless DC drives［J］.IEEE Trans. on IndustryApplications，2007，43(4):1012－1021.

［8］ 安群涛，孙立志，刘超，等.无刷直流电机的磁链自控直接转矩控制［J］.中国电机工程学报，2010，30(12):86－92.

［9］ 夏长亮，张茂华，王迎发，等.永磁无刷直流电机直接转矩控制［J］.中国电机工程学报，2008，28(6):104－409.

［10］ LI Zhenguo，WANG Lu，ZHANG Songfa，et al. Torqueripple reduction in direct torque controlled brushless DC motor［C］//ICEMS2011，2011.

［11］ 李珍国，章松发，周生海，等. 考虑转矩脉动最小化的无刷直流电机直接转矩控制系统［J］.电工技术学报，2014，29(1):139－146.