基于灰色聚类的交叉航路拥挤识别方法
李善梅, 徐肖豪, 王 超, 王 飞
(中国民航大学空中交通管理研究基地,天津300300)
交叉航路是空域中出现航迹交叉的航路构型.由于航迹交叉,两股交通流相互汇聚,导致两航路上航空器之间的侧向间隔逐渐减小,当交通量较大时,航空器之间相互影响严重,引发交叉点附近的交通拥挤现象.文献[1]指出空域耦合单元的复杂态势对空中交通拥挤和延误具有最直接的影响.交叉航路作为目前最具典型性的空域耦合单元类型之一,已成为空中交通运行的瓶颈,有必要对其交通拥挤态势进行识别研究.
目前,有关空中交通拥挤识别方面的研究大多基于对拥挤的基本认识,即在某时段内,由于某空中交通单元(航路、扇区、终端区、区域)的交通需求与其交通容量发生矛盾而引起的交通滞留现象,在此基础上,派生出延误、排队长度、复杂度、管制员工作负荷等指标来衡量空中交通是否拥挤以及拥挤严重程度. 美国的增强型流量管理系统(enhanced traffic management system,ETMS)采用将扇区、定位点和交叉航路的交通需求与事先确定的容量阈值(monitor alert parameter,MAP)相比较,得到交通拥挤状况[2]. 文献[3]将动态密度视为与给定空域范围内航空器密度、交通管制复杂程度相关的管制员工作负荷测度方法,建立了首个动态密度的定量数学模型.文献[4]从几何学的角度分析空域的复杂性,建立了交通密度、汇聚性、分散性和灵敏性4 类复杂性指标,间接描述空域拥挤态势.文献[5]将机场到离场排队延误时间作为机场拥挤的度量指标,并对排队延误时间的传播现象进行研究.文献[6]提出了基于航班排队延误和航班取消数量的拥挤定义方法.文献[7]分析了机场交通需求、容量与航班延误的关系,采用离港航班延误率将延误划分为5 个等级,间接表示机场拥挤程度.文献[8]提出了基于连携效应的交通复杂性测度模型,并对关系性态势和冲突性态势进行了分析.文献[9]通过计算不同速度、不同航向进入的航空器冲突解脱空间的大小来评估扇区拥挤程度.文献[10-11]分别建立了扇区的概率交通需求模型,并将概率需求与MAP 值相比较,建立了扇区拥挤概率预测方法. 文献[12]采用滑行时间描述机场交通的拥挤程度.
以上研究主要存在两方面缺陷:第一,都是基于拥挤某个方面的特征对拥挤进行识别,具有一定的片面性,缺乏从不同的角度对拥挤态势进行识别;第二,延误、排队长度等指标虽然在一定程度上刻画了拥挤状态,但实际上是一种事后评价,具有一定的被动性,不能反映出空中交通拥挤发生、发展的动态变化过程.
基于上述不足,本文首先提出了基于出入交通量的交叉航路交通拥挤的定义;然后,建立了交叉航路拥挤度量指标;最后,建立了基于灰色聚类的交叉航路拥挤识别方法.
1 交叉航路拥挤的定义
目前,国际上对交通拥挤的定义还没有统一的标准.本文从运动交通流的角度出发,认为拥挤的形成过程是流入交通量的累积超过流出交通量的消散,并基于出入交通量及交叉航路交通拥挤的内部特征,提出了交叉航路交通拥挤的定义:交叉航路交通拥挤是指在一定时段和一定交叉航路空间范围内,飞入交通量大于飞出交通量而造成的交叉航路交通负荷增大、交通复杂性提高的飞机滞留现象.
本定义指出:
(1)拥挤形成的过程是流入交通量的累积超过流出交通量的消散;
(2)拥挤形成的位置应该是在一定空间延伸范围的边界上,流入交通量和流出交通量具有匹配关系,满足流量守恒原理;
(3)拥挤的表现主要反映在交通负荷和交通复杂性上.
图1 给出了交叉航路交通拥挤示意图. 图1中,qin为飞入流量,qout为飞出流量,虚线的宽度代表飞入、飞出交通量的大小. 图1(a)中飞入、飞出交通量相同,航空器之间间隔较大,没有明显的跟驰现象,交通负荷和交通复杂性较低.图1(b)中飞入交通量大于飞出交通量,滞留的航空器较多,交通负荷加大,且大部分航空器位于交叉点附近,航空器之间相互影响程度加大,交通复杂性增强.

图1 交叉航路交通拥挤示意图Fig.1 Schematic diagram of crossing air routes congestion
2 交叉航路拥挤指标的建立
交叉航路拥挤是航空器之间的微观相互作用导致的宏观滞留现象,并且是一个动态变化的过程,在建立拥挤指标时要从交叉航路拥挤的宏观、微观及动态特征等方面入手进行研究. 因此,本文建立了交叉航路的拥挤度量指标:表征交叉航路拥挤运动特征的宏观拥挤指标——滞留度指标;表征交叉航路拥挤复杂特征的微观拥挤指标——汇聚度指标;表征交叉航路拥挤负荷特征的静态拥挤指标——当量交通量指标. 通过咨询空管专家,上述指标已基本上反映了交叉航路拥挤的基本特征,并且避免了建立大量指标带来的大计算量和高复杂度以及指标难以量化的问题.下面分别对上述指标的建立过程进行具体阐述.
2.1 交叉航路滞留度指标的建立
基于上述交叉航路交通拥挤定义,根据出入交通量建立滞留度指标,该指标可定义为给定时间范围内,某空域单元飞入交通量与飞出交通量之差与流出交通量的比值. 其中,飞出交通量在一定程度上代表着空域单元的交通服务水平,用滞留度κ 表示飞入交通量超出空域单元交通服务水平的程度,

该指标表征交叉航路交通拥挤的运动特征,反映交叉航路的运行效率,属于相对宏观的度量指标.一般情况下,滞留度越大,交通运行质量越差,越易发生交通拥挤.
2.2 交叉航路汇聚度指标的建立
随着空中交通量的不断增加,目前用于评估空中交通拥挤程度的航空器计量方法已不再适用,空域复杂性在刻画空中交通拥挤态势中发挥着重要作用.因此,交叉航路的复杂结构要求从复杂性的角度来研究其拥挤问题.
图2(a)、图2(b)给出了交叉航路交通流运行对比图. 尽管两图中的航空器架次数相同,但图2(a)中的大部分航空器处于航路交叉点附近且并未通过交叉点,呈现出较强的汇聚态势,交通复杂性较高,为避免飞机相撞,要不断调整飞机的速度和位置,跟驰现象明显;图2(b)中大部分航空器处于航路交叉点之后,且交叉点之前的航空器距离交叉点较远,呈现出较强的发散态势,交通复杂性较低,无须对飞机飞行做过多干预,飞行自由度较高. 因此,图2(a)的交通拥挤程度明显高于图2(b).可见,对于交叉航路来说,汇聚度属于相对微观的度量指标,表示交通复杂程度,影响着交叉航路的交通拥挤态势.

图2 交叉航路交通运行对比Fig.2 Comparison of traffic operation in crossing air routes
本文将汇聚度指标作为描述交叉航路拥挤程度的指标之一.在建立汇聚性测度模型之前,首先需要建立交叉航路模型.
2.2.1 交叉航路模型
交叉航路拥挤主要位于航路交叉点及其附近区域,又由于航空器通过交叉点之后,航空器之间处于发散态势,因此,在计算交叉航路的汇聚度时,只需计算交叉点之前区域内的汇聚度即可.
图3 给出了交叉航路的拓扑结构图.两条航路的交叉点为O,夹角为θ∈[30°,90°].设两条航路宽度均为Wroute=10.8 n mile,航路交叉区宽度为2Lint,Lint可基于航路宽度推导得到,


图3 交叉航路拓扑结构示意图Fig.3 Schematic topology of crossing air routes
区域协调席管制员接收机组计划的水平距离通常为70 n mile,包括正在管制的航空器及将要接受移交的航空器,该距离以外区域的航空器不会引起管制员的任何注意并产生工作负荷[13].因此,可取各航路入口与交叉点O'的距离

计算交叉航路的汇聚度时,只需计算ABOACOOBA区域的交通流产生的汇聚度,忽略不计各航路70 n mile 以外航空器产生的汇聚度.
本文对此交叉航路模型做如下假设:
(1)交叉航路上的航空器均在同一高度层飞行;
(2)两条航路上航空器的航向不变,均沿航路方向飞行;
(3)重型飞机、中型飞机和轻型飞机的标称速度分别为0.14、0.12 和0.10 n mile/s;
(4)航空器冲突解脱可采取降低航空器飞行速度或在其所在航路宽度范围内进行位置偏移.
2.2.2 汇聚度模型
汇聚是动态的时空演变过程,既包括静态的航空器相对几何位置特征,又包括动态的汇聚特征.静态特征即航空器之间的相对距离,距离越小,汇聚度越大;动态特征即航空器之间达到最小安全间隔的时间,时间越短,汇聚度越大.本文采用国际民航组织规定的航空器安全间隔,即5 n mile[14]. 具有相同相对距离的两对航空器对,因其速度不同,航向不同,其汇聚度也可能不同.因此,本节将汇聚的静态和动态特征相结合,建立交叉航路汇聚度模型.下面分别针对航空器汇聚的两种方式(追及汇聚和交叉汇聚),建立汇聚度的计算模型.
(1)追及汇聚度
追及汇聚即同一航路上的两架航空器之间发生汇聚的情况.其拓扑结构如图4 所示,设两航空器在航路中心线的投影之间的相对距离为Dij,且航空器i 距离交叉点较近,二者的速度分别为vi和vj.下面分别从静态和动态两个方面建立追及汇聚度模型.
首先,将距离作为静态汇聚度的分析基础,在相同的航空器飞行速度条件下,相对距离小的航空器对引起的汇聚度肯定大于相对距离较大的航空器对.航空器对相对距离减小的过程即是汇聚度增加的过程.本文采用与内禀类复杂性模型相类似的函数形式[6],追及汇聚度的静态部分可表示为

式中:φ(·)为追及汇聚度函数;Dij为航空器i 与j的距离;λ1、α1为调节参量.
然后,在此基础上,还要考虑航空器对汇聚的动态特征对汇聚度的影响. 相同的相对距离条件下,若vi-vj≥0,航空器对处于发散态势,此种情况下,可不必考虑其动态特征的影响;若vi-vj<0,航空器对处于汇聚态势,且值越大,其汇聚度就越大,此种情况下,还应考虑追及汇聚度的动态部分对式(3)加以修正,

式中:β1为调节参量.

图4 追及汇聚示意图Fig.4 Schematic diagram of chase aggregation
基于上述分析,建立追及汇聚度计算模型:
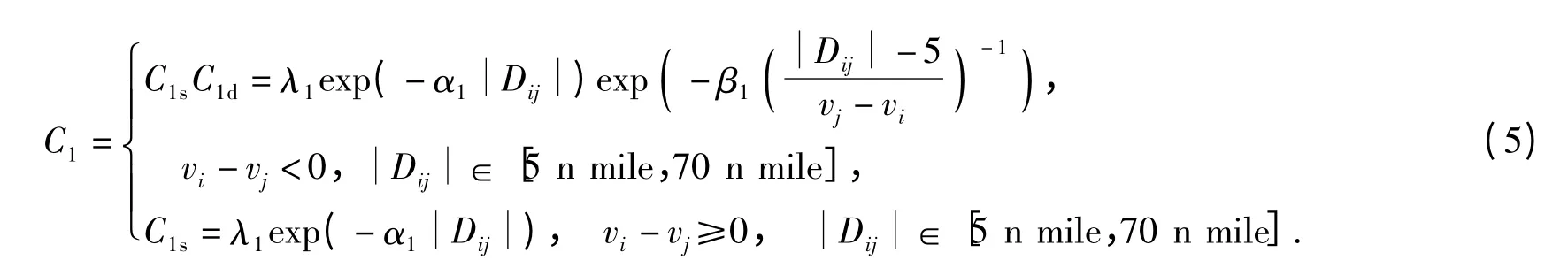
(2)交叉汇聚度
交叉汇聚指分别位于两条交叉航路上的两架航空器之间发生汇聚的情况,其拓扑结构见图5.图5 中,航空器i 与j 之间的相对距离为Dij,航空器i 距离交叉点较近,二者的速度分别为vi和vj.
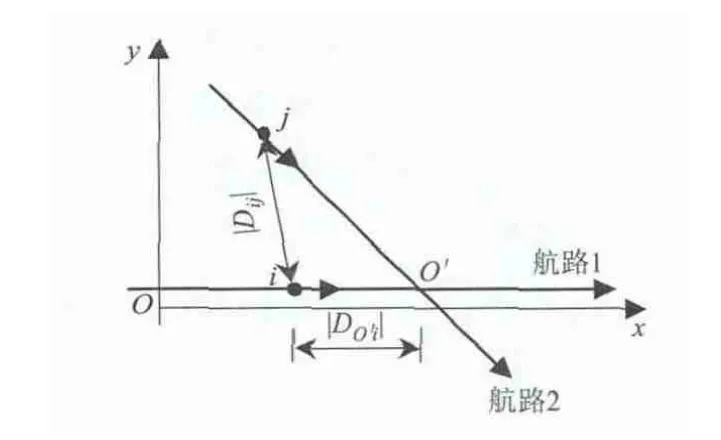
图5 交叉汇聚示意图Fig.5 Schematic diagram of cross aggregation
与追及汇聚度计算模型的建立方法一致,首先考虑交叉汇聚度的静态部分:

式中:φ'(·)为交叉汇聚度函数;
λ2、α2为调节参量.然后,考虑航空器对汇聚的动态特征对汇聚度的影响.由于两架航空器的航向不同,其动态特征即航空器之间达到最小安全间隔所需时间的计算方法与追及汇聚有所不同,不能用简单的相对距离除以相对速度得到,需要建立相对距离关于时间的函数关系式.如图3 所示,以航路1 方向为x 轴,与其垂直方向为y 轴,建立直角坐标系,其中坐标原点距离航路交叉点的距离为70 n mile.设航空器i位于航路1 上,航空器j 位于航路2 上,建立航空器的动力学方程如下:

式中:
xi(t)、xj(t)为航空器i 与航空器j 在时刻t 的横坐标;
yi(t)、yj(t)为航空器i 与航空器j 在时刻t 的纵坐标;
θ 为航路交叉角.
推导出两航空器距离关于时间t 的方程式:

式中:为两航空器初始时刻的距离;
Dij,x(0)为两航空器初始时刻x 方向的距离;
Dij,y(0)为两航空器初始时刻y 方向的距离.令,即:

求解上述一元二次方程可得t1和t2,令两架航空器未来达到最小安全间隔的时间为tmin,分别对以下几种情况加以讨论:
①当式(8)无解时,tmin不存在,两架航空器处于发散状态.
②当t1≥0,t2≥0 时,若t1≤t2,tmin= t1;若t1>t2,tmin=t2.
③当t1≥0,t2<0 时,tmin=t1;当t1<0,t2≥0时,tmin=t2.
④当t1<0,t2<0 时,tmin不存在,两架航空器处于发散状态.
当tmin=0 时,两航空器处于发散态势,不必考虑静态汇聚度的影响;当tmin>0 时,两航空器处于汇聚态势,且tmin越小,汇聚态势越严重,考虑交叉汇聚度的动态部分对式(6)加以修正,即

式中:β2为调节参量.
交叉航空器对的汇聚度为
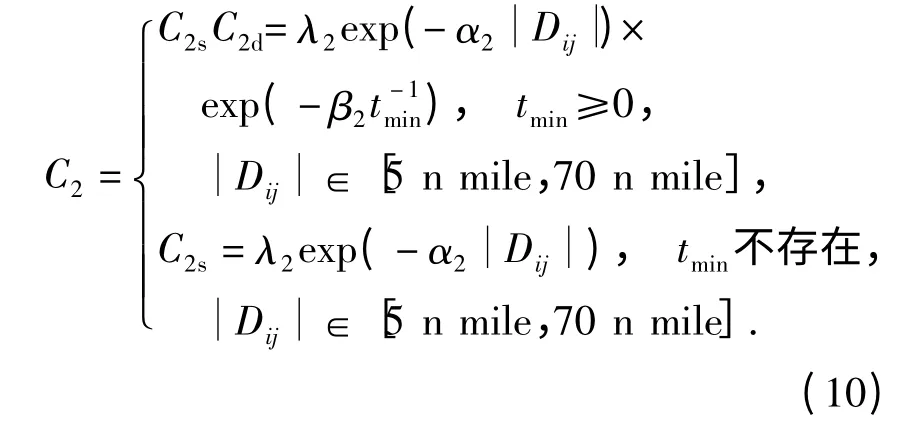
(3)汇聚度
交叉航路的汇聚度等于追及汇聚度与交叉汇聚度之和.另外,还需考虑航空器所处交叉航路的不同阶段对汇聚度的影响,距离交叉点较近的航空器与交叉点的距离越大,对交叉航路总体汇聚性的影响越小.针对不同的,可设定相应权重,以反映其对总体汇聚性的影响. 参考文献[15]并咨询管制专家,发现15、40 和70 n mile是与汇聚度相关的距离阈值.当两航空器间距大于15 n mile 时,航空器对发生飞行冲突的概率很小,因此,管制员一般重点监视间距小于15 n mile 的航空器对;40 n mile 是航路(航线)扇区管制员的一般水平管制范围,管制员接受移交并对该区域内航空器进行监视,开始注意航空器间距小于40 n mile 的航空器对;相距70 n mile 以外的航空器对一般不会对管制员产生任何工作负荷.基于上述距离阈值,对交叉航路进行分段处理,见图6.

图6 交叉航路分段示意图(单位:n mile)Fig.6 Schematic diagram of segmentation of crossing air routes (unit:n mile)
图6 中方格部分为第1 阶段,斜线部分为第2阶段,散点部分为第3 阶段,设)为航空器处于航路不同阶段对汇聚度的影响因子.当时,当时,当时,因此,交叉航路最终的汇聚度模型为
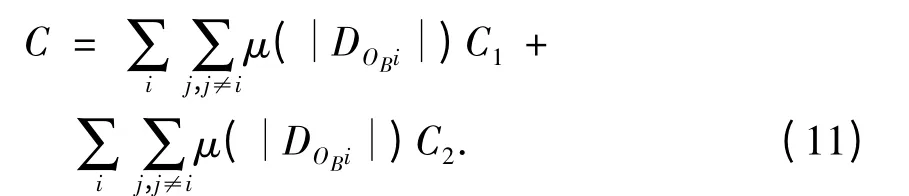
将式(5)和式(10)代入式(11)中,便可求得交叉航路的总汇聚度.
2.3 交叉航路当量交通量指标的建立
交通量指标表征交叉航路的交通负荷,此交通量指标为某时刻交叉航路上包含的航空器总架次,它在一定程度上反映了交叉航路交通流的疏密程度.当滞留度指标和汇聚度指标相同时,交通量越大,交通流的不稳定性越强,也越易发生交通拥挤.不同类型航空器的尺寸及安全间隔各不相同,因此,这里选用当量交通量来描述交叉航路交通拥挤的负荷特征,通过对不同类型航空器数量进行加权求和得到当量交通量:

式中:a、b、c 分别为重型飞机、中型飞机和轻型飞机的架次数;k1、k2、k3为分别为重型飞机、中型飞机和轻型飞机的权重.
通过与空管专家进行沟通交流,本文以轻型航空器作为当量标准,分别取重型飞机、中型飞机和轻型飞机的权重为k1=1.3、k2=1.1 和k3=1.0.
3 交叉航路拥挤的灰色聚类识别
利用雷达管制模拟机,依据国内某交叉航路实际运行数据,编制仿真航路入口处的交通飞行计划及交叉点处的容量时间序列,对交叉航路交通运行情况进行仿真,航路交叉角为45°. 航路上的航空器分为重型、中型、轻型3 类,其标称速度分别为1.4,1.2 和1.0 n mile/10 s.模拟过程中,航空器冲突避让方法可以采取降低航空器的飞行速度或者对航空器进行侧向偏移的方法[16]. 采样间隔为10 s,即每10 s 为一个时间片,统计每一时间片交叉航路上所有航空器的位置坐标及速度数据.
通过咨询管制专家及参考相关文献,对交叉航路的汇聚度作如下约定[13]:航空器对间距5 n mile时的追及汇聚度约为10 n mile 时的3 倍;航空器间距10 n mile 条 件 下,速 度 分别 为0.14 和0.10 n mile/s 的航空器之间的追及汇聚度约为速度均为0.10 n mile/s 的2 倍;航空器间距8.1 n mile条件下,速度分别为0.14 和0.1 n mile/s 的航空器之间的追及汇聚度约为速度均均为0.10 n mile/s的2 倍;间距9.7 n mile、交叉角30°条件下,速度均为0.14 n mile/s 的航空器交叉汇聚度约为处于发散状态的2 倍;间距10 n mile、交叉角90°的航空器交叉汇聚度约为交叉角30°的1.5 倍.通过上述约定,建立相应的约定方程,求解得到汇聚度模型参数的标定值:α1=0.219 7,α2=0.273 3,β1=0.012 5,β2=0. 093 3,λ1=45. 56,λ2=1. 169 1,λ3=51.79,λ4=3.894 5,μ1=1,μ2=0.3,μ3=0.1.
基于上述数据,以5 min 为统计间隔,计算任意一个统计间隔(30 个时间片)的平均汇聚度、平均当量交通量以及整个统计间隔(5 min)的滞留度,作为此统计间隔的交叉航路拥挤指标值. 图7为其中连续26 个统计间隔(共780 个时间片)的当量交通量、汇聚度及滞留度的曲线图.

图7 交叉航路当量交通量、汇聚度与滞留度Fig.7 Curves of equivalent traffic volume,aggregation degree and retention degree
由图7 可见,当量交通量、汇聚度及滞留度的总体变化趋势一致,局部变化特征并非完全同步.例如,第13 个统计间隔的滞留度大幅下降,而当量交通量和汇聚度没有明显波动,其原因是第12 个统计间隔发生交通拥挤后,管制员采取了降低入口流量或提高出口容量所致,而交叉航路内部的平均当量交通量和汇聚度并没有大幅降低.
另外,当平均当量交通量较低时,平均当量交通量和平均汇聚度之间呈现较强的线性关系;当平均当量交通量较高时,二者的非线性关系增强,线性关系减弱.例如,第15 ~19 个统计间隔,平均当量交通量比较平稳,没有太大变化,而平均汇聚度出现了大幅度的变化,突变现象明显.
由于交叉航路拥挤指标的变化具有非线性特性,交叉航路交通系统是一个灰色系统;另外,拥挤是一个人为感知的概念,拥挤的识别具有一定的不确定性和模糊性,各拥挤评价指标与拥挤等级的关系不确定.基于以上两点,很难建立精确的数学模型来描述空中交通拥挤状态.灰色聚类对于具有不确定性、模糊性的灰色系统,能够模仿人脑表达过渡性界限或定性知识经验,实现对不确定性概念的判断,且计算简单[17]. 鉴于此,本文建立了基于灰色聚类的交叉航路拥挤智能识别方法.
3.1 基于灰色聚类的交叉航路拥挤识别步骤
依据灰色聚类的计算流程[18]包括确定聚类评估体系、建立评价矩阵、确定白化权函数、计算聚类权、计算聚类评估值、确定评价结果.交叉航路拥挤识别的具体步骤如下.
(1)确定聚类评估体系.记各个交叉航路拥挤评价时段为聚类对象m,m∈M ={1,2,…,u};拥挤度量指标(即滞留度、饱和度和当量交通量)为聚类指标n,n∈N ={1,2,3};交叉航路交通拥挤状态等级为灰类k,k∈K={1,2,3,4}k 值1 ~4 分别对应畅通、稳定、轻微拥挤、严重拥挤.由此可得,M 为聚类对象集;N 为聚类指标集;K 为灰类集;{M,N,K}为灰色聚类评估体系.
(2)构建评价样本矩阵. 令xmn(m =1,2,…,u;n=1,2,3)为第m 个评价时段对于第n 个拥挤指标的归一化值,X 是以xmn为元素的矩阵,称为评价样本矩阵,则
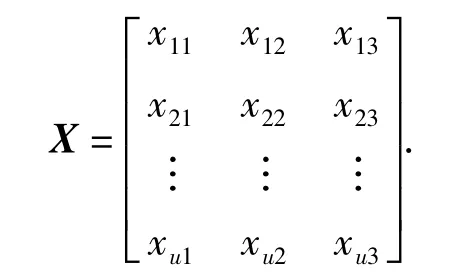
(3)确定白化权函数.将交通拥挤状态等级k看作形态灰类,在认知平面上,以灰类的样本(白化值)xmn为横坐标,记第n 个拥挤指标对于交通拥挤状态等级k 的白化权函数为fnk.
(4)计算聚类权重.记聚类权重为ηnk,

式中:ηnk为第n 个拥挤指标归入第k 个交通状态的聚类权;λnk为第n 个拥挤指标属于第k 个交通拥挤状态的白化值;v 为聚类指标的个数,v=3.
(5)计算聚类评估值. 评价时段m 属于第k个交通拥挤状态的灰色变权聚类系数为
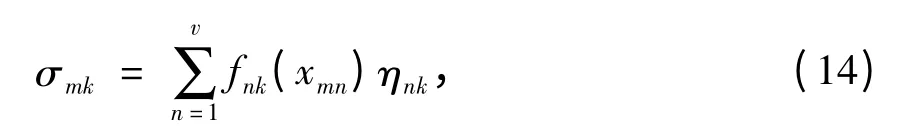
式中:σm=(σm1,σm2,…,σms)为时段m 的聚类系数向量;s 为灰类的个数,s=4.
(6)确定评价时段的交通拥挤状态等级.设

则称时段m 属于第k*个交通拥挤等级.
3.2 白化权函数的确定
本文采用的输入输出变量的白化权函数由上限测度、适中测度和下限测度3 个基本类型构成.其中上限测度和下限测度采用半梯形函数,适中测度采用三角函数,如图8 所示. 将交通拥挤状态划分为4 个等级,建立如图9 所示的白化权函数.

图8 白化权函数基本类型Fig.8 Basic classes of whitening weight function
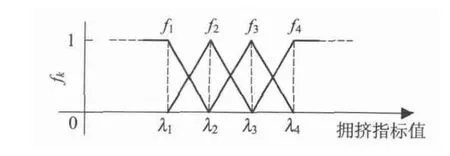
图9 白化权函数的一般形式Fig.9 General form of the whitening weight function
对于某个拥挤指标,分别对应4 个交通拥挤状态等级建立白化权函数:

在交通拥挤识别中,根据交叉航路的自身条件及专家咨询和经验数据等进行综合确定各个拥挤指标的分类标准,不同交叉航路不同时段同一拥挤指标的分类标准有所不同.
4 算例分析
基于第3 节的仿真数据,对本文交叉航路拥挤识别方法进行算例分析,验证方法的有效性. 以某实验中连续10 个统计间隔(300 个时间片)为例,说明本文方法的计算过程.表1 给出了各聚类指标的初始值.

表1 聚类指标初始值Tab.1 Initial value of the clustering index
首先,将3 个聚类指标进行归一化处理.然后,请空管专家对每个拥挤指标的不同拥挤等级进行打分评价,将各专家的打分结果进行综合处理,最终确定各聚类指标的分类标准,如表2 所示.

表2 聚类指标分类标准Tab.2 Classification criteria of the clustering index
将表2 中的分类标准值分别代入式(15)~(18),即可得到各聚类指标的白化权函数. 根据式(13)得出各聚类指标的灰色聚类权,见表3.
最后,依据式(14)得出各时序的灰色变权聚类系数,并根据确定各时序的交叉航路拥挤状态.如表4 所示.
由表4 可见,第4、9 个统计间隔的交叉航路处于严重拥挤状态,第1、5、8 个统计间隔处于轻微拥挤状态.这与仿真过程中在第4、9 两个统计间隔内,管制员做出的冲突避让次数较多,航空器在交叉航路范围内飞行时间较长这一拥挤现象相符.其中,第9 个统计间隔的当量交通量不是很高,但由于其滞留度和汇聚度比较高,交通流的复杂性较高,仍然判定为拥挤状态;尽管第10 个统计间隔的当量交通量较高,但由于其滞留度和汇聚度较低,说明其交通运行秩序良好,最终判定为稳定状态.该算例进一步说明了交叉航路拥挤态势是交通流宏观运动特征和微观复杂特征相互作用的结果.另外,通过与专家打分法得到的识别结果相比较,本文方法识别的准确率高达90%,识别效果较好.

表4 灰色变权聚类系数及归属类划分Tab.4 Variable weights of gray clustering coefficient and classification of attribution categories
5 结束语
本文从交通拥挤的本质出发,提出了基于出入交通量的交叉航路拥挤的定义方法,建立了表征交叉航路拥挤的宏观与微观特征拥挤度量指标,建立了基于灰色聚类的交叉航路拥挤识别方法.算例结果表明,本文方法识别的准确率较高,且计算过程简单,容易编程实现.在实际运行中,该方法可提高空管人员对交叉航路拥挤态势识别的速度及准确性,有助于空管人员及时有效地采取措施,防止交通拥挤的进一步恶化,从而提高交叉航路交通的安全性和运行效率.
下一步将研究空中交通运行其它瓶颈处(例如机场、终端区等)的交通拥挤识别方法. 基于本文提出的交通拥挤运动特征思想,分析不同瓶颈处交通拥挤的特点,分别建立表征拥挤特征的度量指标,更全面和系统地研究空中交通拥挤识别问题.
致谢:中国民航大学科研启动资金项目(2014QD01S).
[1] 张晨,胡明华,张进. 针对交叉流的组合冲中突解脱策略[J]. 系统工程理论与实践,2011,31(6):1165-1173.ZHANG Chen,HU Minghua,ZHANG Jin. Combined conflict resolution strategy to intersecting traffic flows[J]. Systems Engineering:Theory and Practice,2011,31(6):1165-1173.
[2] Volpe National Transportation Systems Center.Enhanced traffic management system (ETMS )functional description[S]. Cambridge: Dept. of Transportation,2002.
[3] LAUDEMAN I V,SHELDEN S G,BRANSTROM R,et al. Dynamic density:an air traffic management metric,NASA/TM-1998-112226[R]. Washington D. C.:NASA,1998.
[4] DELAHAYE D, PUECHMOREL S. Air traffic complexity:towards intrinsic metrics[C]∥3rd USA/Europe ATM R&D Seminar. Napoli:[s.n.],2000:1-6.
[5] WANG P T R,TENE N,WOJCIK L. Relationship between airport congestion and at-gate delay[C]∥Digital Avionics Systems Conference. Irvine:[s. n.],2002:2D5-1-2D5-10.
[6] MUKHERJEE A,LOVELL D J,BALL M O,et al.Modeling delays and cancellation probabilities to support strategic simulations[C]∥Proceedings of 6th USA/Europe Air Traffic Management R&D Seminar.Baltimore:[s. n.],2005:1-10.
[7] 徐涛,丁建立,顾彬,等. 基于增量式排列支持向量机的机场航班延误预警[J]. 航空学报,2009,30(7):1256-1262.XU Tao,DING Jianli,GU Bin,et al. Forecast warning level of flight delays based on incremental ranking support vector machine[J]. Acta Aeronau Tica Et Astronau Tica Sinica,2009,30(7):1256-1262.
[8] 张晨,胡明华,张进,等. 基于交通复杂性的扇区资源管理[J]. 南京航空航天大学学报,2010,42(5):607-613.ZHANG Chen,HU Minghua,ZHANG Jin,et al.Sector asset management based on air traffic complexity[J]. Journal of Nanjing University of Aeronautics & Astronautics,2010,42(5):607-613.
[9] van PAASSEN M M, d'ENGELBRONNER J G,MULDER M. Towards an air traffic control complexity metric based on workspace constraints[C]∥2010 IEEE International Conference on Systems Man and Cybernetics (SMC). [S. l.]:IEEE,2010:654-660.
[10] 王超,杨乐. 空域扇区流量与拥塞预测的概率方法[J]. 西南交通大学学报,2011,46(1):162-166.WANG Chao,YANG Le. Probabilistic methods for airspace sector flow and congestion prediction[J].Journal of Southwest Jiaotong University, 2011,46(1):162-166.
[11] 田文. 基于不确定需求预测的概率空域拥挤管理方法研究[D]. 南京:南京航空航天大学,2011.
[12] KHADILKAR H, BALAKRISHNAN H. Network congestion control of airport surface operations[J].Journal of Guidance,Control and Dynamics,2013:1-7.
[13] 叶博嘉,胡明华,张晨,等. 基于交通结构的空中交通复杂性建模[J]. 交通运输系统工程与信息,2011,12(1):166-172.YE Bojia,HU Minghua,ZHANG Chen,et al. Traffic structure-based air traffic complexity modeling[J].Journal of Transportation Systems Engineering and Information Technology,2011,12(1):166-172.
[14] ICAO. Doc 9869 AN/462 Manual on required communication performance (RCP)[S]. Montreal:International Civil Aviation Organization,2006.
[15] KOPARDEKAR P,MAGYARITS S. Measurement and prediction of dynamic density[C]∥Proceedings of the 5th USA/Europe Air Traffic Management R & D Seminar. Budapest:Hungary,2003:1-8.
[16] 陈勇. 空域容量评估模型和优化方法研究[D]. 北京:北京航空航天大学,2004.
[17] 刘思峰,党耀国,方志耕,等. 灰色系统理论及其应用[M]. 3 版. 北京:科学出版社,2007:74-83.
[18] 贺玲,吴玲达,蔡益朝. 数据挖掘中的聚类算法综述[J]. 计算机应用研究,2007,24(1):10-14.HE Ling, WU Lingda, CAI Yizhao. Survey of clustering algorithms in data mining[J]. Application Research of Computers,2007,24(1):10-14.

