铁路碎石道砟静态压碎行为数值模拟
张 徐, 赵春发, 翟婉明
(西南交通大学牵引动力国家重点实验室,四川 成都610031)
大量现场观测表明,在列车荷载长期往复作用 下,道床内部的碎石道砟会出现不同程度的破碎与粉化现象[1]. 道砟破碎和粉化会导致道床脏污与板结,使道床弹性下降,并增强轮轨动力作用,加快道床宏观残余变形和轨道结构沉降,进而恶化轨面几何状态,加剧轮轨动力作用.如此恶性循环,可能导致轨道结构状态超过安全使用限度,引发行车安全事故.我国既有铁路经过6 次大提速后,干线旅客列车最高时速达到200 km/h 以上;2008 年以来,建成并开通时速200 km/h 以上高速铁路1 万余km(截止2013 年底).伴随我国铁路提速与高速化发展,道砟破碎、粉化导致的有砟轨道道床病害问题日益突出,由道床病害引起的轨道养护维修工作量显著增加,这需要深入研究碎石道砟及散体道床的力学行为与劣化机理,并在掌握道砟破坏和道床变形基本规律的基础上,发展、完善提速及高速有砟轨道结构设计、养护维修理论与方法.
道砟破碎与道砟颗粒强度及其承受的荷载有关,也与道砟材质及其内部应力分布、微裂缝缺陷有关[2],研究单个道砟破碎的细观力学行为有利于揭示道砟颗粒间相互接触导致破碎的机理.国内外学者通过静态压碎试验研究了道砟颗粒的强度特征,如McDowell、苏勇等分别测试了粒径10 ~50 mm 道砟的静态压碎强度,指出单颗粒道砟静态压碎的特征强度服从Weibull 分布[3-5].
室内试验可以获得道砟的破碎强度,结果也可用于数值模型的验证分析,但现有测试技术不能获得加载过程中道砟的内部应力,因此,通过室内试验研究尚不能完全揭示道砟的破碎机理.
用离散元法模拟道砟的静态压碎行为,可以获得压碎过程中道砟内部的应力分布与裂纹扩展进程,便于研究道砟颗粒破碎及道床累积变形机理.Guerrero 等用PFC2D 软件建立了二维轨枕-道床模型,研究了循环荷载作用下道砟破碎对轨道永久变形的影响,发现即使只有少量颗粒发生破碎,也会严重增大轨道永久变形[6];Lim 等采用黏结球形单元,根据加载时单元间黏结键失效来模拟单颗粒道砟的静态压碎行为[7];Ergenzinger 等采用球形单元填充多面体的方法模拟单颗粒道砟的压碎行为[8].
道砟颗粒静态压碎行为的上述离散元模拟研究中,均简化了道砟颗粒的形状,也没有关注压碎过程中道砟内部应力分布与裂纹扩展的演化.
为深入了解碎石道砟静态压碎强度及其压碎过程中的力学行为,我们使用三维激光扫描仪,获得了一些高速铁路特级道砟的真实形态,采用PFC3D 软件构建道砟静态压碎的离散元模型,对碎石道砟静态压碎行为进行数值模拟,重点分析了道砟的压碎强度、压碎过程中内部应力分布、演化以及裂纹扩展过程.
1 道砟静态压碎的离散元分析模型
1.1 道砟几何形态模拟
碎石道砟具有形状不规则、棱角分明、表面纹理粗糙的形态特征. 通常可以采用数码相机、摄影机或CT 设备等提取道砟的几何形态[9-11],但一般仅能获得道砟的二维或部分三维形态特征.为准确获得道砟真实的三维形态,我们使用三维激光扫描仪(图1),获得了道砟表面点云.图2 为单颗道砟的实物照片和扫描获得的三维表面点云,由621 035 个表面点构成.

图1 单个道砟的三维激光扫描Fig.1 3-D laser scanning of a ballast

图2 道砟实物和道砟表面点云Fig.2 A ballast and its surface point cloud
利用扫描获得的道砟三维几何图形,采用成密排六方结构的球形单元填充表面点云围成的区域构建道砟的离散元模型.图3 为分别采用半径r =1,2,5 mm 的球形单元构建的道砟的离散元模型.由图3 可见,球形单元半径越小,道砟离散元模型的几何形态越真实.显然,对于同一道砟,采用的球形单元半径越小,模拟精度越高,但所需单元数量也越多,这将导致模型的求解规模越大,计算时间越长.因此,为了兼顾模拟精度与计算效率,经试算对比后,采用半径为2 mm 的球形单元.
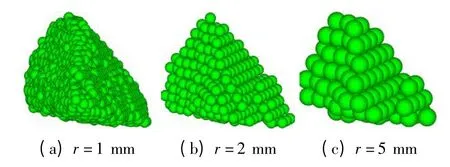
图3 道砟离散元模型Fig.3 Discrete element models for a ballast
1.2 接触模型与黏结断裂准则
道砟材料的本构行为通过球形单元间的接触与黏结实现. 采用线弹性接触本构模型[12]计算单元间的接触力,加载前在相互接触的球形单元间定义接触黏结,黏结断裂准则为:

式中:Fn和Fs分别为法向和切向接触力标量,法向接触力以受压为正;φn和φs分别为法向和切向接触黏接强度.
当单元间接触力均不满足式(1)和(2)时,黏结不会发生断裂;当单元间接触力满足式(1)或(2)中之一时,接触黏结将发生断裂,法向和切向接触黏接强度均失效,此后两单元若再发生接触,其法向和切向接触力不再受式(1)和(2)限制. 加载过程中,模型中黏结断裂的数量逐渐增加,可以直观模拟道砟在载荷作用下内部裂纹萌生、扩展直至破碎的过程.
1.3 模型参数选取
为了使离散元模型能获得可靠的宏观响应,一般需要根据材料的宏观特性来标定单元颗粒的细观参数[13-15].将两相互接触的球形单元等效为长度为两接触球体半径之和的弹性梁,根据拉压和抗弯刚度等效的原则,可以建立材料宏观特性与颗粒细观参数的关系[12].对于花岗岩材料的道砟,参考试验获得的花岗岩的宏观特性参数[16-17],计算出离散元模型的微观参数值,见表1.

表1 离散元模型的微观参数Tab.1 Micro parameters in the discrete element models
1.4 加载方式与加载速率
以黏结的球形单元填充扫描获得的碎石道砟的三维几何形状,以相互平行的两刚性平板模拟试验机压头,建立碎石道砟静态压碎的离散元模型,见图4.加载时下加载板固定,上加载板以恒定的速率v 向下加载板移动,同时记录施加在上加载板的载荷大小和位移量. 通常,试验机压头的刚度远高于岩石刚度,而且金属压头较为光滑,故取加载平板的刚度为5 GN/m,摩擦因数为0.1. 此外,取模型中局部惯性阻尼系数为0.7,忽略材料的粘性阻尼.
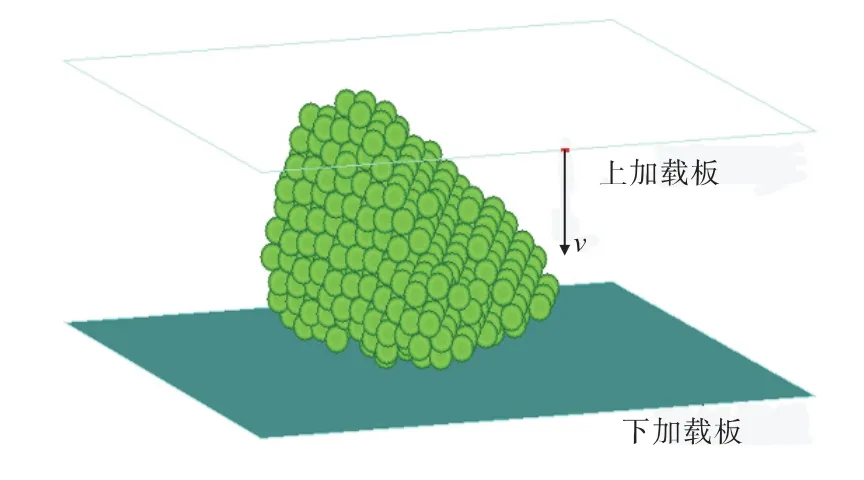
图4 道砟静态压碎的离散元模型Fig.4 Discrete element model for static crushed behavior of a ballast
对同一道砟,分别以v =0.1,1.0,10.0 mm/s的加载速率模拟其静态压碎过程.数值模拟结果表明,3 种加载速率下的载荷-位移历程基本重合,载荷峰值差异极小;加载速率为0.1 和1.0 mm/s 时,道砟破碎过程中的单元黏结断裂数N 十分接近;但是,当加载速率提高到10.0 mm/s 时,单元黏结断裂数明显降低. 可见,过大的加载速率会引起一定的惯性冲击,导致道砟压碎过程呈现出不同的破坏方式,故下文计算中采用v =1.0 mm/s 的加载速率.
2 碎石道砟静态压碎强度统计分析
McDowell 等根据加载时施加在道砟上的载荷F 和上、下加载平板之间的距离d 定义道砟的特征应力σ 为[3]:

当F 取加载过程中的载荷峰值,d 取道砟破坏时加载平板间的距离时,将由式(3)得到的特征应力定义为碎石道砟静态压碎特征强度.
与岩石强度的点载荷试验结果一样,道砟静态压碎试验获得的特征强度也呈现很大的离散性.McDowell、苏勇等的研究表明,道砟静态压碎特征强度服从Weibull 概率分布[3-5],即特征应力为σ时道砟的残存概率Ps满足:
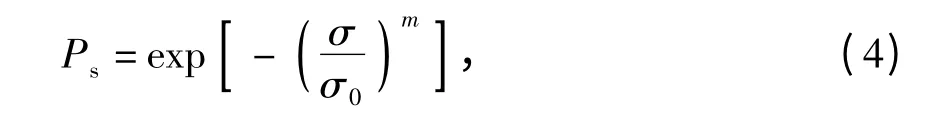
式中:σ0是残存概率为37%时的特征应力;m 为Weibull 系数.
根据高速铁路特级碎石道砟的级配要求,采用离散元法,模拟分析了粒径分别为30 ~40、40 ~50和50 ~60 mm 共27 颗道砟的静态压碎行为.经统计分析得到不同粒径道砟特征强度的残存概率分布,见图5(x 表示横坐标,y 表示纵坐标,R 为相关系数). 图5 中还给出了相应的线性拟合公式、拟合曲线以及残存概率为37%时的Weibull统计特征强度.
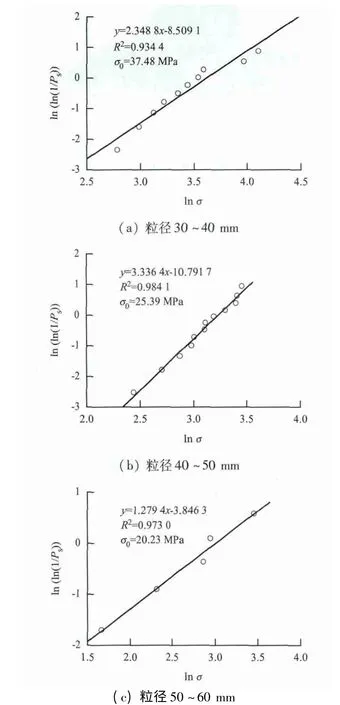
图5 不同粒径道砟静态压碎特征强度的Weibull 分布Fig.5 Weibull survival probability of railway ballast with different particle sizes
ln(ln(1/Ps))与ln σ 的高度线性相关性表明,用Weibull 分布能够较好地描述碎石道砟静态压碎时特征强度的分布规律.
从图5 还可见:
(1)粒径30 ~40、40 ~50 和50 ~60 mm 的碎石道砟的Weibull 系数m 分别为2.348 8、3.336 4和1.279 4,对应的残存概率为37%的特征强度分别为37.48、25.39 和20.23 MPa,与试验结果[3-4]接近,说明建立的离散元模型合理,计算结果有较高的可信度.
(2)粒径越大,道砟残存概率为37%的特征强度越小.
进一步分析表明,碎石道砟静态压碎残存概率为37%的特征强度与其平均粒径具有近似的线性相关性.
3 碎石道砟静态压碎的力学行为
碎石道砟静态压碎时,不仅压碎强度离散性大,压碎过程中道砟内部应力分布与裂隙扩展过程也存在差异.但是,道砟从初始加载至最终整体破坏,其静态压碎过程基本包含4 个阶段:颗粒转动、局部破碎、弹性响应和整体破坏阶段[18].需要指出的是,在某个确定道砟的静态压碎过程中,有可能多个阶段不出现,也有可能某个阶段在加载过程中多次出现,这与道砟的形态特征、加载压头与道砟接触位置等有关.
建立某确定道砟的离散元模型,模型包含658 个半径为2 mm 的球形单元,所有单元间初始接触黏结数为3 162 个.为揭示该道砟静态受压时的破碎机理,从载荷-位移响应、内部接触力链演化与裂隙扩展三方面分析道砟静态压碎过程中不同阶段的力学行为.
图6 给出了该道砟加载前和压碎后的离散元模型.图6(b)表明,该道砟经静态压缩后发生整体破坏,分裂成2 个主要碎块.
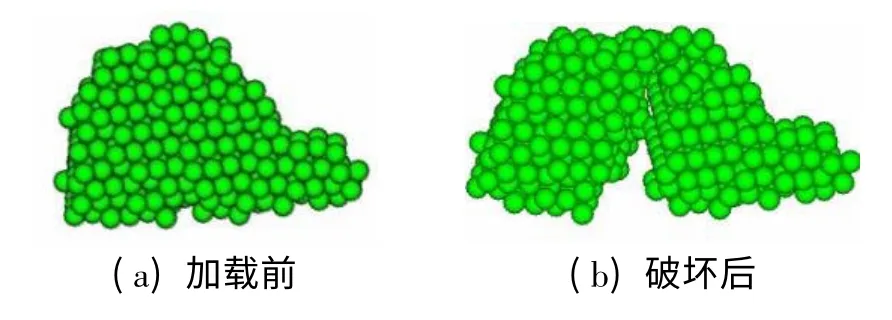
图6 道砟在静态压碎前、后的离散元模型Fig.6 Discrete element models of a ballast when it is intact and crushed
3.1 载荷-位移响应
图7 为道砟从初始加载到整体破坏的载荷-位移(F-s)响应曲线.初始加载时,由于道砟与下加载板的接触表面不平整,载荷作用下道砟发生转动,此时载荷处于极低水平;道砟转动至稳定位置后,与上、下加载板的作用点逐渐固定,处于较稳定的受力状态,道砟变形量线性增大;当加载位移增大到0.396 mm 时,道砟与加载板接触点附近局部产生微小破碎,道砟发生第2 次轻微转动,此时载荷急剧减小至接近于0,表明上加载板与道砟基本上处于脱离接触的状态;当加载位移以恒定速率继续增大时,上加载板与道砟重新接触,道砟再次进入稳定受力状态,载荷随位移增大线性增大;最后,随载荷和位移的进一步增大,道砟内部部分应力超过黏结强度,内部产生裂纹并迅速扩展,导致道砟整体破坏,载荷瞬间减小至0.
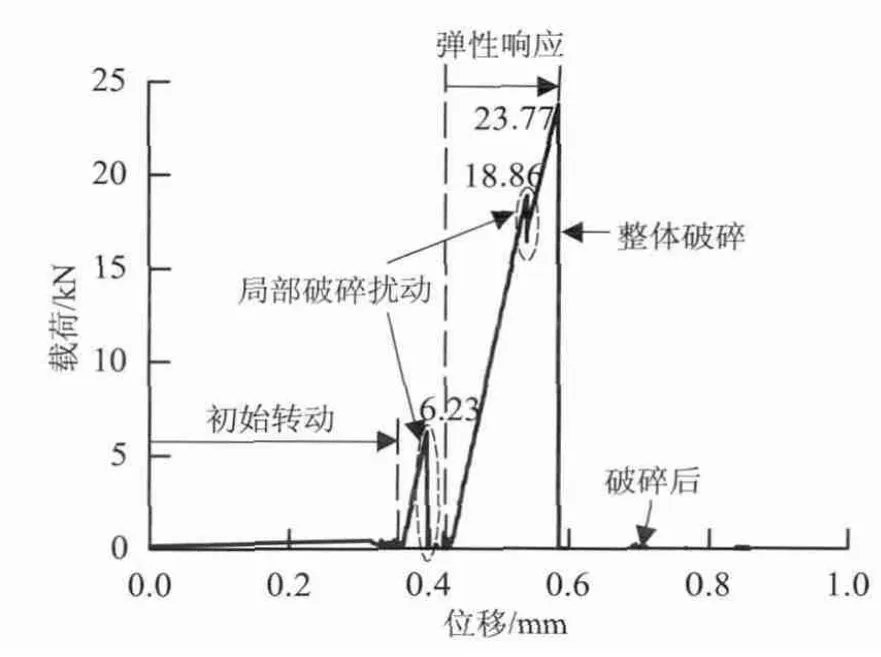
图7 道砟静态压碎过程中载荷-位移响应历程Fig.7 Load-displacement history in ballast crush process
3.2 道砟内部力链分布及其演变
为掌握静态压碎过程中道砟内部发生的细观力学行为,图8 给出了不同阶段道砟内部接触力链的分布及其演变过程. 图8 中,连接两接触单元球心的实线表示单元间的接触力,红色表示压力,绿色表示拉力,线条越粗则接触力幅值越大.
图8(a)为初始稳定阶段道砟内部接触力链的分布,表明道砟与两加载板间形成了几个稳定的接触点,这些点处的接触力明显高于道砟内部单元的接触力,符合道砟受压时载荷从表面若干个接触点向内部传递的自然规律.
图8(b)为载荷达到6.23 kN 时,道砟内部接触力链的分布. 结合载荷-位移响应曲线(图7)可知,当载荷从0 增大到6.23 kN 时,道砟与下加载板之间某个接触点附近发生局部破碎,打破了道砟与加载板之间的稳定接触状态,道砟发生第2 次转动.
道砟第2 次转动后,加载位移继续增大,加载板上的载荷从0 开始重新增大.图8(c)给出了载荷重新达到6.14 kN 时道砟内部接触力链的分布.对比图8(b)和8(c)可见,道砟与下加载板的接触点位置明显变化,且道砟内部力链的分布也发生了较大变化.
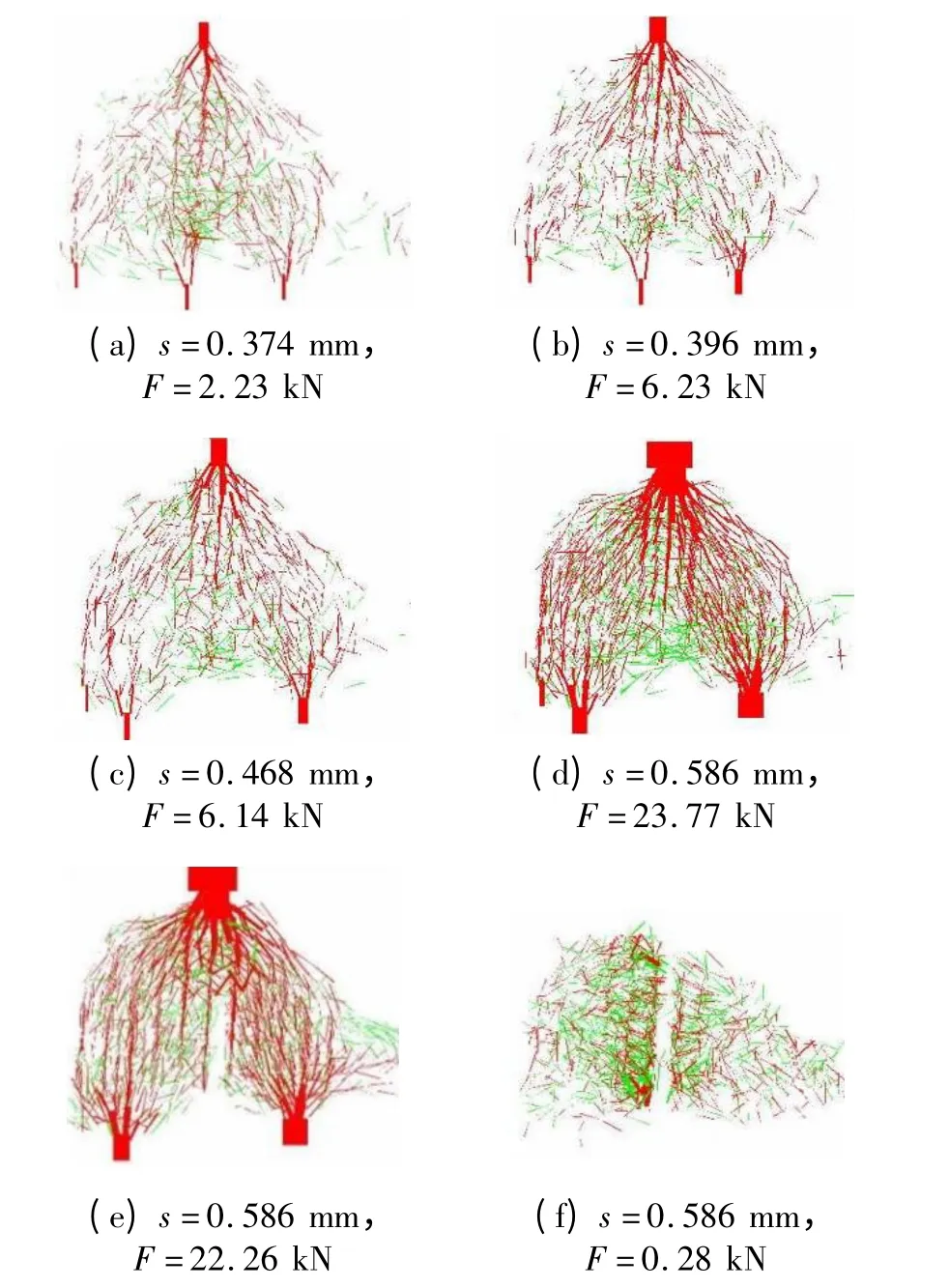
图8 道砟静态压碎过程中内部接触力链的演化Fig.8 Evolution of force chain distribution in the crush process
图8(d)~8(f)为道砟从承受最大荷载到瞬间破碎时内部力链的分布.图8(d)显示,当载荷达到23.77 kN 时,道砟下部局部区域集中出现单元接触拉力,相当数量的单元接触力超过其黏接强度,道砟内部出现了一定规模的黏结断裂,形成微裂隙并迅速沿主力链方向扩展,最终导致道砟整体破坏.图8(f)表明,当道砟破碎为2 个碎块后,上加载板与道砟脱离接触,2 个碎块之间不再有力链连接,碎块内部的力链分布基本恢复到自然状态.
3.3 道砟内部黏结断裂及其分布
图9 为静态压碎过程中道砟内部单元接触黏结断裂数随载荷的变化曲线.根据道砟内部单元接触黏结断裂数随载荷增大的快慢,可将道砟从内部裂隙萌生到整体破坏过程分为3 个阶段:裂隙萌生与聚集、裂隙急剧扩展和道砟整体破坏. 在裂隙萌生与聚集阶段,当载荷从0 增大到23.77 kN 时,虽然道砟内部黏结断裂数由0 增加到40 个,道砟内部出现若干微裂纹,但总体上载荷与加载位移近似成正比关系(见图7),表明道砟整体上处于弹性变形,并具有相当大的承载能力;在裂隙急剧扩展阶段,内部黏结断裂数瞬间增加到168 个,道砟内部已经出现裂缝,同时伴随着载荷减小,表明道砟承载能力开始下降;在道砟整体破坏阶段,黏结断裂数快速增加到267 个,载荷急剧下降,道砟已经失去承载能力.

图9 静态压碎过程中内部黏结断裂数随载荷的变化Fig.9 Number of broken contact bonds vs. load in the crush process
图10 为静态压碎过程中不同阶段道砟内部黏结断裂的分布(红色方块表示黏结断裂的位置).图10(a)显示,当载荷首次达到6.23 kN 时,由于道砟与加载板接触点处存在应力集中,下加载板接触点附近出现1 处黏结断裂. 当道砟发生轻微转动、重新稳定受载后,载荷随加载位移持续增大,道砟内部黏结断裂并没有迅速增加,主要以整体弹性变形来承受外部载荷.直到载荷达到13.60 kN 时,道砟内部出现第2 处黏结断裂,位于上加载板与道砟接触点附近(图10(b)). 当载荷进一步增大到18.86 kN 时(图10(c)),道砟与上、下加载板接触点附近黏结断裂数增加到8 个,这一区域的集中断裂使得道砟出现较大的局部压缩变形,道砟与加载板接触状态突然发生轻微变化,载荷在较短时间内下降到16.64 kN,且应力集中区域黏结断裂出现连锁反应,黏结断裂数快速增加到15 个.
图10(d)显示,当载荷达到峰值23.77 kN 时,道砟内部黏结断裂数为40 个,且大多集中在沿加载方向的某一平面或其附近区域.该区域大致位于道砟与下加载板接触面中部的上方,承受剪切力和较大的弯矩.此时,道砟在该区域开始形成集中的微裂隙,并沿加载方向迅速扩展,当加载位移进一步增大时载荷开始下降. 图10(e)表明,当载荷由峰值降到22.26 kN 时,黏结断裂数由40 个急剧增加到168 个,说明道砟在整体破坏前期裂隙扩展十分迅速.比较图10(d)和10(e)可知,大量新增黏结断裂多出现在黏结断裂面的扩展面上,且主要沿加载方向向上迅速发展,形成明显的断裂面. 这一断裂面在图10(e)中更为清晰,而且可以发现,在断裂面处单元间已经不再接触.
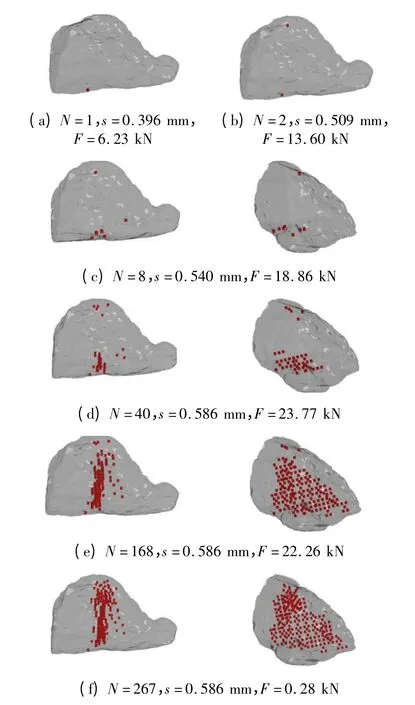
图10 道砟静态压碎过程中黏结断裂分布的演化Fig.10 Evolution of the distribution of broken bonds in the crush process
继续加载时,道砟整体破坏.图10(f)显示,在较小的载荷作用下,道砟内部黏结断裂数快速增加到267 个,黏结断裂面已沿加载方向贯穿整个道砟,使道砟迅速劈裂成2 个碎块.
4 结 论
本文中采用激光扫描仪获得铁路碎石道砟的真实三维几何形态,建立了道砟静态压碎的离散元模型,对道砟静态压碎行为进行了数值模拟,通过统计道砟静态压碎的特征强度,分析了道砟压碎过程中载荷-位移响应、内部力链分布与演化以及单元接触黏结断裂的发展过程,得到以下结论:
(1)道砟静态压碎的特征强度服从Weibull分布,道砟平均粒径增大时,其残存概率为37%的特征强度会降低,这与已有试验结果一致. 说明所建立的道砟静态压碎离散元模型正确,模型参数选取合理,可供铁路散体道床细、宏观力学行为及状态劣化模拟研究参考.
(2)道砟尖锐棱角和表面不平整容易引起道砟发生翻转和局部压碎,导致道砟外部接触状态发生微弱变化,载荷也出现短暂回落;道砟稳定受载时,载荷与加载位移近似成正比;道砟内部裂纹快速扩展和整体破坏阶段,载荷急剧减小.
(3)道砟与加载板接触点处的接触力明显高于道砟内部单元的接触力;道砟外部接触状态发生变化会导致其内部接触力链分布明显变化;道砟稳定受载时,内部接触力链分布稳定,随加载位移增大,内部黏结断裂数逐渐增大;当载荷达到峰值后,内部黏结断裂数急剧增加,道砟劈裂破碎.
致谢:西南交通大学科技创新项目(2682014CX043).参考文献:
[1] 曾树谷. 铁路散粒体道床[M]. 北京:中国铁道出版社,1997:30-57.
[2] AURSUDKIJ B. A laboratory study of railway ballast behaviour under traffic loading and tamping maintenance[D]. Nottingham:University of Nottingham,2007.
[3] MCDOWELL G R,LIM W L,COLLOP A. Measuring the strength of railway ballast[J]. Ground Engineering,2003,36(1):25-28.
[4] LIM W L,MCDOWELL G R,COLLOP A C. The application of Weibull statistics to the strength of railway ballast[J]. Granular Matter,2004,6(4):229-237.
[5] 苏勇. 含沙铁路道碴力学行为研究[D]. 大连:大连理工大学工程力学系,2011.
[6] LOBO G S,VALLEJO L E. Discrete element method analysis of railtrack ballast degradation during cyclic loading[J]. Granular Matter,2006,8(3/4):195-204.
[7] LIM W L, MCDOWELL G R. Discrete element modelling of railway ballast[J]. Granular Matter,2005,7(1):19-29.
[8] ERGENZINGER C,SEIFRIED R,EBERHARD P. A discrete element model predicting the strength of ballast stones[J]. Computers & Structures,2012,108:3-13.
[9] FERELLEC J F,MCDOWELL G R. A method to model realistic particle shape and inertia in DEM[J].Granular Matter,2010,12(5):459-467.
[10] 杜欣,曾亚武,高睿. 基于CT 扫描的不规则外形颗粒三维离散元建模[J]. 上海交通大学学报,2011,45(5):711-715.DU Xin,ZENG Yawu,GAO Rui. 3D modelling of irregular shape particles for discrete element method based on X-ray tomography[J]. Journal of Shanghai Jiaotong University,2011,45(5):711-715.
[11] ANOCHIE B J K,KOMBA J,TUTUMLUER E.Aggregate surface areas quantified through laser measurements for South African asphalt mixtures[J].Journal of Transportation Engineering,2012,138(8):1006-1015.
[12] Itasca Consulting Group,Inc. Particle flow code in 3 dimensions (PFC3D)[M]. 4th ed. Minneapolis,MN:Itasca Consulting Group,Inc.,2008:3-11-3-21.
[13] STAHL M, KONIETZKY H. Discrete element simulation of ballast and gravel under special consideration of grain-shape,grain-size and relative density[J]. Granular Matter,2011,13(4):417-428.
[14] WANG Y,TONON F. Modeling Lac du Bonnet granite using a discrete element model[J]. International Journal of Rock Mechanics and Mining Sciences,2009,46(7):1124-1135.
[15] WANG Y,TONON F. Calibration of a discrete element model for intact rock up to its peak strength[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2010,34(5):447-469.
[16] POTYONDY D O,CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(8):1329-1364.
[17] 王渭明,杨更社,张向东,等. 岩石力学[M]. 徐州:中国矿业大学出版社,2010:36-48.
[18] CAVARRETTA I,O'SULLIVAN C. The mechanics of rigid irregular particles subject to uniaxial compression[J]. Geotechnique,2012,62(8):681-692.

