可转换债券市场和股票市场的波动性——基于ARCH 族模型和误差修正模型的检验分析

孙晓晓

(安徽财经大学 金融学院，安徽 蚌埠 233000)

19 世纪40 年代，美国发行了第一只可转换债券，由于这种转股期权可以使投资者规避当前时刻直接投资股票的风险，而且可以选择在未来分享发行公司的潜在资本收益，所以被投资者广泛接受。可转换债券对于我国的资本市场而言是一种“舶来品”，自1992 年第一只可转债发行至今，经历了二十余年曲折的发展历史。1997 年出台的《可转换公司债券管理暂行办法》拉开了对符合条件的重点国有企业进行可转换债券的试点发行的序幕。2001 年4 月，证监会发布的《上市公司发行可转换公司债券实施办法》则使我国可转债市场进入了一个新的全面发展阶段。截止目前为止，沪深两市仍在交易中的可转债数量已达28 只，融资总额高达1590.07 亿元，还有多只可分离债券，可转债市场颇具规模。可转换债券市场的发展在一定程度上解决了我国资本市场上股权融资比例较高，缺乏创新型金融产品的现象，是我国金融市场的有益补充;同时，给投资者提供了一个新的投资工具，对于拓宽企业融资渠道、促进金融市场繁荣发展、提升企业竞争力也有着重要意义。在此背景下，研究可转债市场的波动特征及其与股票市场的波动关系对于促进我国可转债市场健康发展，维持证券市场的稳定有着重要意义。

一、文献回顾

我国的可转债市场只有二十几年的发展历史，而且国内学者对可转债的研究主要集中在定价以及可转债市场与股票市场的波动关系方面。赖其男、姚长辉、王志诚运用Matlab 软件并结合二叉树方法对选取的可转债样本进行理论价值分析与定价。［1］黄建兵从无风险套利角度出发，对我国证券市场上可转换债券价格及其标的股票价格之间的关系进行分析，据此推断我国证券市场上价格的有效性。［2］尹韵、费方域对可转债市场价格与标的股票市盈率之间关系进行研究，认为二者之间的关系之所以不显著是因为我国资本市场较低的有效性使得市盈率无法真实反映投资者对公司股票价格的未来预期。［3］张敏运用协整理论、BEKK－GARCH 模型、VAR 模型对可转债指数与沪深300 指数之间的动态传导进行实证分析，认为虽然部分可转债与其基础股票价格之间不存在长期协整关系，但就整个市场而言，这种长期协整关系是存在的;另外，两个市场的收益率序列的条件波动之间存在着较强的正相关性。［5］张秀艳、张敏对可转债指数和沪深300 指数进行建模并提取方差、协方差，模拟计算出了两个市场的动态相关系数，研究结果显示，两个市场对共同信息的反映速度和收益率变化程度是相近的。［6］胡秋灵、张苏凤、王宁利用DCC－GARCH 模型对可转债市场与股票市场的动态相关系数进行研究，他们认为DCC－GARCH 模型对二者的动态关系研究是可行的。

由以上综述不难看出，围绕可转换债券的研究多是从其自身定价和与股票市场关系为主题。本文除了通过建立误差修正模型研究二者的长期均衡关系之外，单独分析了可转债市场收益率的波动特征以及其与股票市场的波动溢出效应。

二、样本数据说明

文章采用的数据来自大智慧软件和Wind 金融资讯终端。由于目前在二级市场上交易的28 只可转债中有19 只是在上海证交所上市，而且上证可转债指数以2002 年12 月31 日为基日，与2014 年8 月份刚刚发布的深证转债指数相比较为成熟，所以选取上证可转债指数(000139)作为研究对象，相应的标的股票市场指数为上证指数(000001)。时间口径方面，以能在大智慧软件上取得的数据为基础，样本日期从2004 年1 月8 日至2014 年11月20 日，共得2637 个日收盘价作为样本数据，以pt表示。由于样本数据选取的是时间序列数据，为了保证序列的稳定性，定义收益率rt= 100% ×［lnpt－lnpt－1］，经处理后得到2636 个数据，上证可转债指数收益率用rcb表示，上证指数收益率用rsz表示。本文采用Eviews6.0 作为分析软件。

四、实证分析

(一)问题的提出

为了研究可转换债券市场和其与股票市场的波动性，提出以下假设:

1. 利好、利空信息对可转债收益率的冲击是不对称的;

2. 可转债市场与股票市场之间存在单向溢出效应;

3. 上证指数收益率和上证可转债指数收益率之间存在着长期均衡关系，其自身的约束机制会修正外界因素带来的误差，使二者趋于均衡。

(二)可转债市场收益率的实证分析

1. 收益率序列的描述性统计

图1 上证可转债指数收益率rcb的描述性统计量

由图1 可以看出，样本期内，上证可转债指数收益率rcb的均值为0.0358%，标准差为1.0293%;JB统计量为12934.76，且伴随概率为0，表明其拒绝序列服从正态分布的假定;偏度S=－0.9203 ＜0，峰度K=13.6948 ＞3，说明r 具有左偏、尖峰的特点。

2. 收益率序列的平稳性检验

对时间序列进行平稳性检验主要是为了排除可能出现的伪回归现象，常用的平稳性检验方法有ADF 检验、DF 检验和PP 检验，本文采用ADF 检验验证上证可转债指数收益率的平稳性。观察上证可转债指数收益率的线形图可以发现，检验样本的原始图形呈现出无规则上升、下降并反复，应该不含截距项与常数项;滞后项的选择根据AIC、SC最小准则确定(滞后项为3)。对序列进行ADF 检验的结果如表1 所示，可以看出，在1%的显著水平下，样本数据ADF 值都显著小于1%的临界值，说明rcb为平稳的时间序列数据。

表1 序列 的ADF 检验结果

3. ARCH 效应检验

由于上证可转债指数收益率的波动呈现群集现象和异方差效应，因此对序列进行ARCH 效应检验。观察上证可转债指数日收益率序列的偏自相关图可以发现，其与滞后1 阶、3 阶、15 阶、18 阶、21 阶相关性较强。建立上证可转债指数日收益率的高阶自回归模型:

rt= 0.209810rt－1+ 0.055675rt－3+ 0.071247rt－15+0.072687rt－18－0.056784rt－21

(0.0000)(0.0036)(0.0002)(0.0002)(0.0030)

其中，括号内为变量估计系数t 检验的伴随概率，可以看出所有变量的t 检验均通过，系数都比较显著，上式说明上证可转债指数收益率的滞后1、3、15、18、21 阶对收益率当前的变化具有较强的影响。提取自回归模型的残差并作残差平方的序列图，如图4 和图5 所示:

图2 上证可转债指数收益率高阶自回归模型残差图

图3 上证可转债指数收益率高阶自回归模型残差平方序列图

从残差图可看出，残差的波动有聚类的现象，残差平方序列图也出现了聚类现象，这说明误差项可能具有条件异方差(ARCH 效应)。采用ARCH－LM 检验来验证上证可转债指数收益率序列是否存在ARCH 效应，经过反复试验，当滞后长度为8时，AIC 和SC 值较合理，因此进行滞后长度为8的ARCH－LM 检验。由表2 可知，ARCH－LM 检验统计量的P 值远小于显著性水平α = 0.01 ，故拒绝原假设，残差存在ARCH (8)效应。

表2 收益率残差序列自相关LM 检验(滞后长度:8)

4. GARCH 族模型

(1)GARCH (1，1)模型

GARCH 模型既可以描述单个金融资产的风险变动，还可以描述不同金融资产之间的风险变动关系和收益的相关性变化，因此，广泛应用于在对金融数据的实证分析中。本文采用的GARCH 模型是在实证分析中较常用的GARCH (1，1)模型。

首先采用GARCH (1，1)模型对上证可转债指数日收益率进行实证分析。上证可转债指数日收益率的GARCH 模型:

rcb= 0.184595rcb，t－1+0.045262rcb，t－3+0.055511rcb，t－18－0.037683rcb，t－21+ εt

(0.0000)(0.0280)(0.0038)(0.0314)ht= 0.00000121 +.128851ε2

t－1+0.861273ht－1(0.0000)(0.0000)(0.0000)

(AIC=－7.065556 SC=－7.049845)

由于在建立GARCH 模型的均值方程时，rcb，t－15的系数项未通过t 检验，故剔除。均值方程中所有系数均通过t 检验，且ARCH 项与GARCH项的和小于1，满足了参数的约束条件，这说明上证可转债指数收益率的条件方差是平稳的;又因为二者的和(0.990124)很接近于1，所以随机冲击对条件方差的影响有一定的持续性，其对未来的预测具有一定的作用。

(2)TARCH 模型

国内外学者对于股票市场的研究发现，股价的上升幅度和下跌幅度相同时，股价下跌过程往往伴随更剧烈的波动，TARCH 模型可以用于解释这种非对称性。通过建立TARCH 模型来考察信息对上证可转债指数收益率冲击的对称性。上证可转债指数收益率的TARCH 模型:

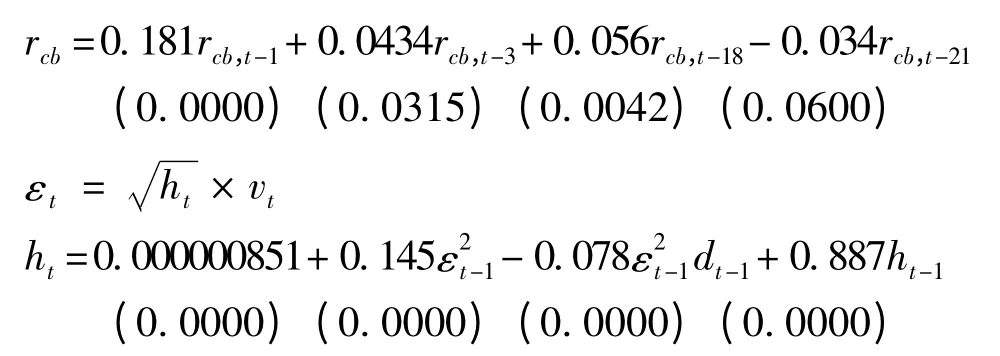
从TARCH (1，1)模型中可以看出，杠杆效应系数ф = 0.078315 ≠0 ，说明信息对上证可转债指数收益率的影响是非对称的;且由于ф ＜0，非对称效应的作用会使波动减小，但是并不存在杠杆效应。另外，ARCH 项与GARCH 项之和接近于1，说明上证可转债指数的过去波动对指数未来走势的冲击是持久的。

(三)可转债市场与股票市场的波动溢出效应分析

波动溢出效应实质上是“金融传染”的一种表现，是指一个市场的波动不仅对自身未来有影响，还有可能对其它市场未来的波动产生影响。由于可转债的行权受标的股票价格走势、股价波动率、上市公司基本面等因素影响，与股票市场关系密切，而且两个市场也都受到宏观经济环境和金融政策的影响，其波动性也具有相互影响的关系。所以研究两个市场的波动溢出效应，对于发展可转债市场，维持两个市场的稳定都具有重要意义。

对上证指数(000001)的日收盘价同样进行收益率处理，平稳性检验和LM 检验，检验结果显示收益率的滞后6 阶对收益率当前的变化具有较强的影响，建立上证可转债指数日收益率的高阶自回归模型:

括号内为变量估计系数的t 检验的伴随概率，可以看出所有变量的t 检验均通过，变量的系数都比较显著，说明收益率的滞后6、15、阶对收益率当前的变化具有较强的影响。同样对上证指数收益率进行GARCH (1，1)建模，模型如下:

由于建模时 的系数项未通过t 检验，故剔除。均值方程中所有系数均通过t 检验，且ARCH 项与GARCH 项的和小于1，满足了参数的约束条件，说明上证可转债指数收益率的条件方差是平稳的。提取模型残差，与上证可转债指数收益率GARCH(1，1)模型的残差进行Granger 因果关系检验得出如下结果:

表3 滞后6 期条件下的Granger 因果关系检验结果

由表4 可以看出，在5%的显著性水平下可以任务股票市场的波动是可转债市场波动的格兰杰原因，这初步证明了两个市场间存在溢出效应，但是是不对称的，单向的，这说明了股票市场的波动对可转债市场的波动具有引导作用，股票市场在二者的波动关系中起基础性作用。

(四)上证可转债指数与上证指数之间的长期均衡关系

两个经济变量之间经常会存在长期均衡的关系，但是这种长期均衡关系从短期来看可能是失衡的，此时可以建立误差修正模型来调整这种长短期失衡，使得一个期间的失衡部分就可以在下一期得到纠正。

1. 与 的协整分析

由前文分析可知上证可转债指数收益率序列和上证指数收益率序列均是平稳序列，所以利用E－G 两步法来检验两个变量之间的协整关系。首先用最小二乘估计法估计上证指数日收益率关于上证可转债指数日收益率的方程:

rsz=－0.000208 +1.026192rcb+ εt

提取模型残差并用ADF 检验法对回归残差做平稳性检验，结果如表4 所示:

表4 εt 的单位根检验结果

由表4 的检验结果可知，残差是平稳序列，所以两个收益率序列之间存在着协整关系。当两个序列存在协整关系时，可以认为尽管两个经济变量短期内有时失衡，但经济自身的力量会使其重新回到均衡状态，即短期内无论如何变化，长期来看仍然趋于均衡。上述分析显示，上证指数收益率和上证可转债指数收益率之间存在着某种长期均衡关系。

2. 误差修正模型(ECM)的建立

误差修正模型是由萨甘在1964 年提出的，它既可以描述变量长期关系，又可以描述短期关系。有由上文分析得出 和 之间存在协整关系，可以建立ECM 模型。通过最小二乘法回归得到如下结果:

rsz= 1.047882rcb－0.184724ecmt－1

其中，ecmt= rsz－1.026192rcb+0.000208 ，方程的拟合优度，系数的t 检验和DW 检验均通过，且误差修正系数为负，符合反向修正机制。从ECM 模型中可以看出，短期内上证指数的变动收到上证可转债指数变动的影响，股票市场在不断修正前期误差的过程中使得自身与可转债市场保持动态均衡关系;外界因素的冲击，例如宏观经济政策，会使两个市场的收益率暂时发生偏离，但是其自身的约束机制也会使二者趋于均衡;ECM 项系数反映了误差调整的速度。方程中的ECM 项系数较小，说明上证指数日收益率对误差调整的速度很慢。

三、结论及政策建议

本文通过对2004 年1 月8 日至2014 年11 月20 日的上证可转债指数日收益率与上证指数日收益率进行实证分析得出如下结论:

第一，上证可转债指数收益率序列呈现非对称性，表现为左偏;收益率序列是平稳序列，但是存在高阶ARCH 效应，所以利用GARCH 模型对上证可转债收益率序列进行分析是可行的;同时，通过TARCH 模型证明了虽然利好、利空信息对上证可转债指数收益率的影响存在非对称性，但是却不具有杠杆效应，这与其他学者的研究结论相违背，其原因可能在于样本数据的选取上有所差异。

第二，通过对上证指数收益率和上证可转债指数收益率的GARCH 模型残差进行Granger 因果关系检验，初步验证了可转债市场与股票市场之间存在单向的波动溢出效应，即股票市场的波动导致了可转债市场的波动，而不是相反。这是由于可转换债券是基于标的股票的特殊债券，可以看作是期权与债券的结合，所以，标的股票价格的波动对可转换债券价格的波动具有影响作用，股票市场的波动是导致可转债市场的波动的原因。

第三，通过对两个收益率序列的ECM 模型分析得出上证指数收益率和上证可转债指数收益率之间存在着某种长期均衡关系，而外界因素的冲击，例如利空、利好信息的出现，会使两个市场的收益率暂时发生偏离，但是其自身的约束机制不断修正，促使二者在长期内回归均衡。

可转债市场作为我国金融市场的有益补充部分，在推动金融工具的创新，拓宽企业融资渠道等方面具有十分重要的意义。可转债市场与股票市场作为金融市场的两个重要的子市场，二者之间的波动关系对于金融环境的稳定有着重要作用。因此，应将国外发展可转债市场的经验与我国资本市场的发展现状进行有机结合，对可转债市场的准入制度和交易制度进行创新，在市场稳定的前提下，给予可转债市场更大的发展空间;同时应加强对投资者的教育和合理的引导，培育成熟、理性的可转债投资者。

四、结语

可转换债券是我国引入的为数不多的金融衍生品之一，其在我国的发展时间不长，市场也不完善，所以可供选择的分析指标也比较少，本文中选取的上证可转债指数也只能反映在沪市交易的可转债的情况，相对而言较为片面，这也是需要改进的地方。第二，关于可转债市场与股票市场波动溢出效应分析这部分内容只是初步研究，选用的Granger 因果关系检验方法自身可能会因为对样本数据的处理而产生与理论或实际情况不符合的结果，仍需要进一步改善。第三，从ECM 模型可以看出两个市场之间存在着某种长期均衡关系，但是可能存在个例，即单只可转债和其标的股票之间可能不存在这种长期均衡关系，这种情况也值得进一步研究。

［1］赖其男，姚长辉，王志诚. 关于我国可转换债券定价的实证研究［J］. 金融研究，2005，(9):105－121.

［2］黄建兵. 中国的可转换债券与市场价格有效性研究［J］. 系统工程理论方法应用，2002，(1):63－67.

［3］尹韵，费方域. 可转换债券市场价格与其基准股票市盈率关系初探［J］. 上海管理科学，2005，(1):16－17.

［4］张苏凤. 中国可转债市场与股票市场间联动关系研究［D］. 陕西师范大学，2011.

［5］张秀艳，张敏. 可转换债券市场与股票市场的波动关系——基于二元GARCH 模型的实证研究［J］. 吉林大学社会科学学报，2009，(4):133－140.

［6］胡秋灵，张苏凤，王宁. 中国可转债市场与股票市场的动态关系研究——基DCC－MGARCH 模型的分析［J］.经济与管理，2010，(11):26－31.