Matlab 环境下直线特征匹配中笛卡尔积的应用
胡海霞,李 钢
(1. 宜春学院 物理科学与工程技术学院;2. 宜春学院 数学与计算机科学学院,江西 宜春 336000)
笛卡尔积属于集合论的范畴,[1]设A、B 为任意集合,以A 的成员为第一元素,B 的成员为第二元素构造序偶,由所有这样的序偶组成的集合称为A 与B 的笛卡尔积。笛卡尔积在密码学[1]、数据库数据质量[2]、视觉运动分析[3]等方面都有广泛应用。比如在密码学中,根据笛卡儿积的结构特点,从工程应用的角度构造出基于笛卡尔积的各阶欺骗概率相等的最优Cartesian 认证码。[1]在数据库数据质量方面,利用笛卡尔积运算进行数据库数据质量的分析。[2]视觉运动分析中常常利用序列图像中的直线特征,匹配出序列图像中对应的直线特征,从而进行运动分析估计及三维重建。
但是直线的匹配一直是个难点,[4]传统的直线编组匹配算法[3]使用了笛卡尔积运算,但是这种方法存在计算量巨大、计算复杂的问题。因此,本文提出一种改进的直线匹配算法,该算法采用分步笛卡尔积运算、逐步过滤的方法,以解决传统的直线编组匹配算法中的计算量巨大问题。
1 分步笛卡尔积运算
一般地,直线编组匹配算法中需要两幅图像,一幅模板图像,一幅待匹配图像,分别提取出两副图像的直线特征,数量分别为M、N 条,直线特征组成的有序集合分别记为IA= {a1,a2,…,aM}(1 ≤i ≤M),IB= {b1,b2,…,bN}(1 ≤i ≤N),其中ai、bj分别表示两幅图像中的第i、j 条线段。匹配算法的目标是在待匹配图像中找到一个有序的特征线段组,组中的线段能与模板图像IA中的特征线段一一对应匹配。直线编组匹配算法的步骤如下图1 所示。

图1 直线编组匹配算法的步骤
S1:根据文献[5]定义好的线段对几何二元关系表达式(2)和(3),分别在模板图像和待匹配图像中计算线段对(am,an)和线段对(bs,bt)的二元关系值。
S2:根据模板图像中的线段对(am,an)和待匹配图像中的线段对(bs,bt)的二元关系值,采用文献[5]中的公式(10)计算线段对的粗匹配相似度SL(am,an,bs,bt)。
S3:用阈值Th1过滤SL,得到SL≥Th1的所有四元组(am,an,bs,bt)。根据四元组生成每条模板特征线段ai(1≤i≤M)的候选线段集合Ui,方法如下:
(1)找出m =i 的所有四元组(ai,an,bs,bt),再在(ai,an,bs,bt)中,针对n =j(1≤j ≤M,j ≠i)分别找出四元组(ai,aj,bs,bt),此时,将(ai,aj,bs,bt)中对应的所有s 组成集合Vij。
(2)找出n = i 的所有四元组(am,ai,bs,bt),再在(am,ai,bs,bt)中,针对m = j(1 ≤j ≤M,j ≠i)分别找出四元组(aj,ai,bs,bt),此时,将(aj,ai,bs,bt)中对应的所有t 组成集合V'ij。
(3)将Vij和V'ij中的数据求交集,即Ui=
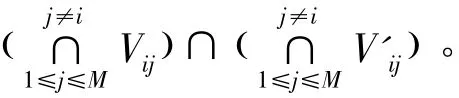
S4:利用所有的候选线段集合Ui(1 ≤i ≤M),采用分步笛卡尔积运算,再用阈值Th2逐步过滤,最后生成模板特征的候选匹配线段组。生成过程示意图如下图2 所示:
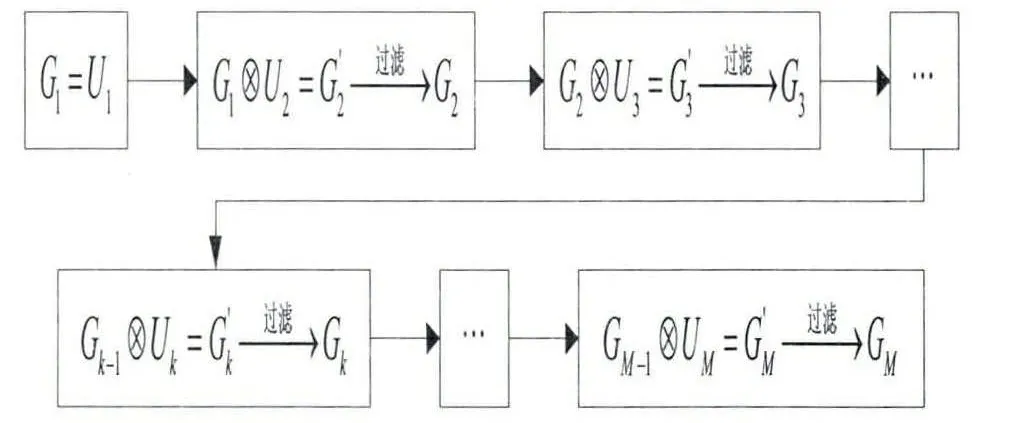
图2 生成候选匹配线段组的过程
(1)分步笛卡尔积运算:首先设G1= U1,然后将G1与U2做笛卡尔积运算得到G'2,用阈值Th2对G'2进行过滤得到G2,再G2与U3做笛卡尔积运算得到G'3,用阈值Th2对G'3进行过滤得到G3,依此类推,最后得到候选线段组集合GM。
(2)逐步过滤的方法:以G'k→过滤Gk(1 <i≤k)为例,设G'k= {(c1,c2,…,ck)}(ci∈IB),表明ai与ci是对应匹配的。首先计算G'k中每个元素(c1,c2,…,ck)的相似度Sk(S1=0 ),表达式为Sk= Sk-1+(SL(ai,ak,ci,ck)+SL(ai,ak,ci,ck))。再用阈值Th2过滤出Sk/(k(k-1))≥Th2的元素而得到Gk。
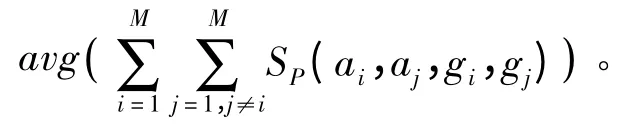
S6:选取GM中匹配相似度SG最大的元素作为最后的匹配线段组。
2 分布笛卡尔积运算的核心代码
由于直线匹配算法的代码量很大,在此仅列出S3 和S4 两部分的核心代码。
S3 的核心代码:
%过滤出SL≥Th1的四元组(am,an,bs,bt)
tmp=find(SL(:,5)>=Th1);
%SL= {(am,an,bs,bt,SL(am,an,bs,bt))}
SL_Filter=SL(tmp(:),:);
%生成每条模板特征线段的候选线段集合U
U=cell(1,M);%定义U
for i=1:M
U{i}=1:N;%初始化


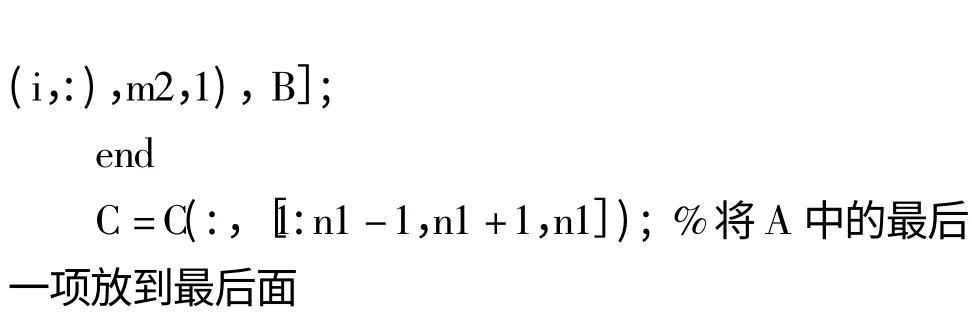
3 实验
实验平台为Matlab 2011b。实验采用一组真实的卫星图像,如图3 所示。图3(a)为模板图像,图3(c)为待匹配图像;图3(b)模板线特征图,线特征均为6 条;图3(d)为待匹配线特征图,线特征分别为51 条;图3(e)为实验所得线段组匹配结果图像。
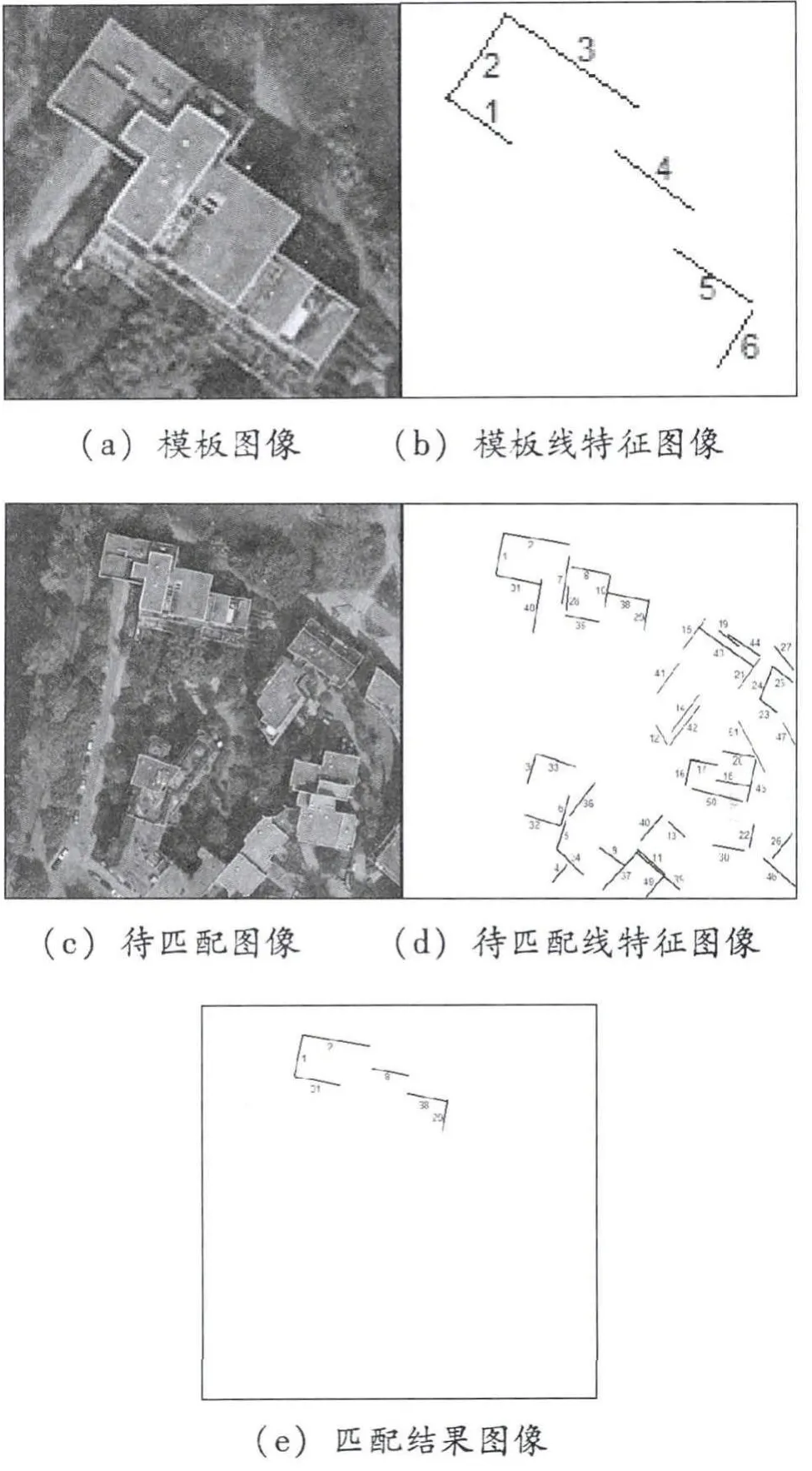
图3 实验图像
实验所取的两个阈值分别为Th1= 0.85 和Th2= 0.9 ,实验中得到的相关数据如下表1 所示。比较表中“本文方法所得线段组数量”和“直接笛卡尔积所得候选线段组数量”两项数据,表明本文算法大大减少了候选线段组数量,极大地提高了直线匹配的效率。

表1 实验中得到的相关数据
4 结论
本文研究了笛卡尔积运算在图像间直线特征匹配中的应用,针对运用传统的直线编组匹配方法中采用直接笛卡尔积运算存在的计算量巨大、计算复杂等问题,提出了一种改进的算法,该算法详细介绍了采用分步笛卡尔积、逐步过滤的过程,并列出了Matlab 环境下的主要核心程序代码。实验表明本文所提算法大大减少了候选线段集数量,并验证了整个直线特征匹配的高效性和有效性。
[1]刘金龙,许宗泽. 笛卡尔积与认证码[J]. 电子与信息学报,2008,30(6):1441-1444.
[2]陈卫东,张维明. 笛卡尔积运算对数据库数据质量的传递影响[J]. 计算机科学,2008,35(6):210-213.
[3]HP Sang,KM Lee,UL Sang.A line feature matching technique based on an eigenvector approach[J].Computer Vision & Image Understanding,2000,77(3):263-283.
[4] Schmid C,Zisserman A.Automatic line matching across views[J].IEEE Computer Vision and Pattern Recognition,1997,17(19):666-671.
[5]胡海霞,李钢. 几何特性二元关系的直线匹配[J]. 中国图象图形学报,2014,19(9):1338-1348.

