原型到模型：生活中数学元素的价值探寻

陈怀娄

一、缘起——生活中的数学“如此重要”

有很多数学内容在生活中都能找到它的原型所在，这些以生活现象为原型的问题常常在教科书中出现。数学源自于人们在生产生活中的发现、思考、总结。生活中有大量随处可见的数学原型，但在学生的眼中却不以为然、视而不见。因此为数学找个原型，引导学生从生活元素中提取数学，让学生经历数学活动的全过程，能让学生热爱数学并重塑数学学习的自信心。我们的数学课堂需要富有生活气息的课堂，需要唤起学生学习数学的热情，这对培养学生浓厚的学习兴趣、探索意识和实践能力有很大帮助。

二、调查——生活与数学“狭路相逢”

1.调查对象

调查对象是乡镇驻地的四年级学生。

2.调查内容

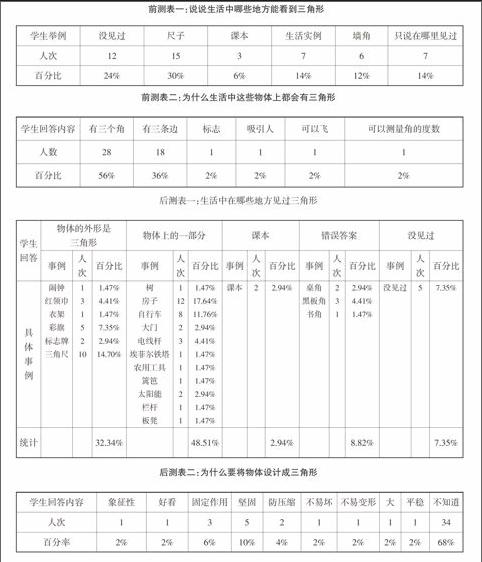
（1）说说生活中哪些地方能看到三角形。

（2）为什么生活中这些物体上都会有三角形？

4.调查结论

（1）没有观察生活就没有元素的储存。

（2）没有思考生活就没有发现问题、提出问题的激情。

（3）没有体验生活就没有深入的理解。

三、探寻——生活中的数学元素“何去何从”

良好的数学教育并不是单纯地使学生掌握更多的数学知识、练就高超的解题技能、取得优异的数学成绩。良好的数学教育应让学生学会运用数学思维进行思考、体悟数学的内在价值、养成良好的学习习惯、获得初步的创新意识和实事求是的科学态度等。良好的数学教育应承担“数学育人”的责任，让学生学会思维，学会学习，从而为学生未来的生活和学习打下坚实的基础。良好的数学教育的课程内容不仅要符合数学本身的特点、体现数学学科的精神实质，还要符合学生的认知规律和心理特点，贴近学生的生活实际。

1.积累生活现象，促进概念理解

案例：园林工人在植树时，会将大株的绿化树木用支架固定起来。这一现象在我们的生活中比较常见，虽然在此现象中没有三角形的出现，但引导学生对此类现象进行发现问题、提出问题、分析问题直至解决问题的系列思考有助于学生深入理解、认识三角形的特性。

2.还原具体情境，沟通经验与数学的联系

案例：刘松执教苏教版四年级《四则运算的复习课》为例谈谈对生活原型的理解。课始，刘老师以115-15×4为例追问：“为什么要先乘除后加减？”面对这样一个数学问题，作为教师的你有答案吗？可想而知，面对这本已掌握并且熟练运用的运算顺序，问为什么要这样做，学生的回答可真是五花八门。有的说这是规定，有的说这是老师告诉的，有的说乘法是二级运算应先算二级再算一级运算，还有的说乘法大减法小、小的要听大的……就是没有说到为什么。在全班20余次不合理回答后，刘松老师仍然没有放弃。最后刘老师以“算式从哪儿来”引导学生认识算式是从具体情境而来，它有具体的问题支撑。在一个又一个的具体情境中学生体会了为什么要先算乘法再算减法，最后刘老师指出数学是活的不是死的，数学也是有生命的，我们要为数学注入生命。

为数学找个原型，把常识提炼为数学，经历数学活动的全过程，能让我们的数学课堂富有生活的气息，唤起学生学习数学的热情。因此，我们不能把课本中的数学知识当作一种真理教给学生，也不应该要求学生以成人化的理解方式去接受数学知识，而应联系我们的生活实际，在众多的原型面前去理解数学、体验数学、建构数学。

3.丰富表象积累，获得良好体验

案例：从感受不到的数学到亲历数学

为了让学生更好地体会数学就在身边，生活中处处有数学，所以要带学生走出教室。从走出教室的第一步起，让学生说说看到了什么？（有的学生说看到了门、墙。）

师：门，门上会有哪些数学知识？（角）

师：角在哪，去摸出来。

师：这是多少度的角？没有测量你是怎么知道的？

师：关于角你还有什么问题？

师：在设计安装时，工人是用什么工具进行测量施工的，他们用的工具与我们学习所用的工具有什么不同？为什么？

师：这些玻璃上有多少个角？工人在操作时需要多少次才能完成？（这时学生开始数起来。）

提示：除了刚才的数，还有其他的方法吗？（计算）

4.适时抽象本质，凸显数学思想

案例：化曲为直的逆向思考

化曲为直的一个现象的解释是在学习圆的周长时将圆的周长在直尺上滚动，有的通过用线绕圆一周然后将线拉直测量线段的长度。在这里，我们能否换个角度思考：化曲为直这一现象在生活中有哪些应用，为什么可以这样运用？怎样用我们的数学知识解释这一现象呢？

出示方砖的图片，这是建筑工人常用的建筑材料之一。如果你是工人的话，让你用方砖来建一个我们学过的平面图形，你会将它建成什么图形？

追问：为什么没有人用方砖建一个圆呢？

学生思考讨论。

得出假结论：用方砖不可能围成圆这种曲线图形。

出示生活中圆形建筑的图片。

反问：它是用什么材料建成的，怎么建成的，为什么可以用方砖建成圆呢？有什么数学原理吗？

向学生介绍“割圆术”，让学生经历正多边形到圆的形成过程，引导学生观察体验，随着边数越来越多，正多边形越来越像圆，感受极限思想。刘徽指出：“割之弥细，所失弥少。割之又割，以至于不可割，则与圆周合体而无所失矣。”这就是说，圆内接正多边形的边数无限增加的时候，它的周长的极限是圆周长，它的面积的极限是圆面积。

5.模拟生活空间，培养数学素养

原型不仅能启发学生在正确理解和解决数学问题上找到捷径，而且能为学生创造、想象的发展提供了广阔的空间。它的意义绝不仅仅在于被当作模具来完成塑像任务，它是创造、创新的“点金石”。正因为有了原型的启发，人们才插上联想的翅膀，把知识不断完善，把技术不断更新。而这种突破原型框架、优化解题方案的过程，正是创造性思想形成和发展的过程。日常生活中熟悉的、具体的生活现象，有利于抽象的数学概念具体化、形象化，有助于学生对概念外延的理解、对概念内涵的掌握。我们应使学生在操作、观察、讨论、交流、归纳、猜想、分析和整理的过程中，理解数学问题的提出、数学概念的形成、数学结论的获得与验证，以及数学知识的应用，从而培养学生的综合素养。