某下承式系杆拱桥静动荷载试验研究

罗晓英

（山西长治公路勘察设计院，山西 长治 046000）

0 引言

随着交通量的不断提高，部分桥梁的承载能力及刚度已经无法达到要求，确定桥梁的承载能力与刚度非常重要，静动荷载试验能测定出桥梁主结构在标准荷载下的强度、应力和变形，以判断主结构的破坏程度与现有承载能力。荷载试验分为静力荷载试验与动力荷载试验两种，其目的是了解结构在荷载作用下的实际工作状态，综合分析判断桥梁结构的承载能力和使用条件。白雨运用有限元分析软件MIDAS Civil建立菜园坝长江大桥有限元模型，制定菜园坝长江大桥主桥静载试验方案，确定控制截面、加载方式、加载位置和加载吨位，测试并分析了静载工况下各测试截面应力、主梁挠度[1]；王战国详细介绍了荷载试验的内容和方法,理论值与荷载试验的测试结果较好吻合,证明了建模方法的可靠性[2]；刘军采用有限元分析软件MIDAS对清水河工业南桥进行成桥状态静力计算,得知车行道桥面系的受力情况是影响本桥结构安全与否的重要条件[3]；崔宝帅以四川省乐山市外环线200 m主跨飞燕式系杆拱桥的设计方案为研究背景,运用有限元软件MIDAS Civil建立了基于梁单元的全桥空间有限元模型，计算分析了桥梁在施工全过程各阶段和运营阶段的静力性能和动力性能[4]；丘弋介绍了某系杆拱桥的荷载试验过程,讨论了其承载能力评定的方法[5]；王刚对某系杆拱桥进行了现场动力荷载试验,对桥梁结构的主要控制断面进行了多种工况荷载作用下的动力性能测试，重点对桥梁结构整体试验模态进行了测试分析，同时结合有限元分析方法对该桥进行了理论分析计算[6]；胡国领通过南水北调总干渠上85 m跨径的某钢管混凝土系杆拱桥荷载试验与理论分析，对比检验了桥梁结构的设计与施工质量，评估了桥梁结构的承载能力[7]；高文博对某下承式混凝土刚性系杆拱桥进行了荷载试验及数据分析，采用大型有限元程序MIDAS建立空间梁格模型，并进行了仿真分析；对多种试验工况下桥梁变形和截面应力的实测值与理论值进行了比较[8]；刘刚采用梁单元、索单元建立了该拱桥有限元模型，按照荷载试验方案中的工况进行了静力分析，建模时采用等代法对钢管混凝土进行了处理，将计算结果与试验结果进行了对比[9]；尹锡军通过对某下承式预应力混凝土系杆拱桥进行的动力荷载试验,将试验数据与理论数据和相关规范值进行了对比分析[10]。

本文结合某下承式系杆拱实例，分析了该桥的静载试验和动载试验，结果表明该桥技术状况良好。

1 静载试验

静载试验主要是通过在桥梁结构上施加与设计荷载或使用荷载基本相当的外载，采用分级加载的方法，利用检测仪器测试桥梁结构的控制部位与控制截面在各级试验荷载作用下的挠度、应力、裂缝、横向分布系数等特性的变化，将测试结果与结构按相应荷载作用下的计算值与有关规范规定值作比较，从而评定桥梁结构的承载能力。

1.1 测试内容

a）系杆及拱肋正应力；b）索力测试；c）系杆竖向挠度；d）拱肋竖向挠度；e）偏载效应及偏载增大系数。

1.2 结构计算

对主桥系杆拱结构进行静载试验，该系杆拱计算跨径80 m，经综合考虑，静载试验主要测试主梁各控制截面或构件的最大内力，根据其内力包络图，确定其内力最不利位置。为保证试验顺利实施，试验跨段加载时采用分级加载形式。

采用有限元软件建立桥梁模型，并对其进行静载试验的理论分析，图1为计算模型图，图2为恒载下拱桥吊索索力分布图。

图1 桥梁有限元模型

图2 吊杆恒载索力分布图（单位：kN）

弯矩包络图如图3所示。根据《公路桥梁承载能力检测评定规程》(JTG/T J21—2011)，并经过结构分析计算确定该桥的内力控制断面。

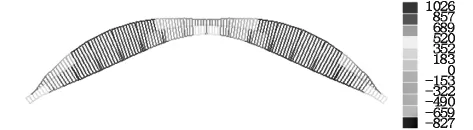
图3 汽车荷载设计弯矩包络图（单位：kN·m）

经过分析，在设计荷载及试验荷载作用下，确定3个主要内力控制截面，即拱肋L/4、L/2及3L/4截面，并确定7个静载试验工况。

静载试验工况：

a）工况1 拱肋L/2截面S1最大正弯矩测试（中载），8号吊索最大索力测试（中载）。

b）工况2 拱肋L/2截面S1最大正弯矩测试（偏载），8号吊索最大索力测试（偏载）。

c）工况3 拱肋L/4截面S2最大正弯矩测试（中载），拱肋3L/4截面S3最大负弯矩测试（中载）。

d）工况4 拱肋L/4截面S2最大正弯矩测试（偏载），拱肋3L/4截面S3最大负弯矩测试（偏载）。

e）工况5 拱肋L/4截面S2最大负弯矩测试（中载），拱肋3L/4截面S3最大负弯矩测试（中载）。

f）工况6 拱肋L/4截面S2最大负弯矩测试（偏载），拱肋3L/4截面S3最大负弯矩测试（偏载）。

g）工况7 恒载作用下，除靠近拱脚的4根吊杆外，全桥共26根吊杆索力测试。

静力试验荷载采用载重汽车进行等效加载。就某一检验项目而言，根据《公路桥梁承载能力检测评定规程》中的规定，桥梁荷载试验一般采用基本荷载，其中静力试验荷载的效率系数η取值范围为0.95≤η≤1.05。在实际加载过程中，为了减少试验时间及简化工况的目的，在保证主要检验项目荷载系数满足要求的前提下，可适当减少或加大某些项目的荷载效率系数，但荷载效率系数的增大必须保证结构的安全。

1.3 加载工况与测点布置

1.3.1 试验荷载

该桥设计荷载为公路-Ⅱ级，经过计算，本试验共需加载车4辆，单车总重为30 t，轴重分配为6 t、12 t、12 t。加载车辆需逐一称重、编号，单车总重误差不得超过±1 t。

1.3.2 加载工况

首先测试了恒载下的吊杆索力。索力测试结束后，对各测点应变计和采集记录仪器工作的可靠性进行了检验，经检验无误后，方可进行正式的荷载加载试验。该桥为新建桥梁，因此在正式试验之前，对结构进行2次预加载，通过预加载使结构进入正常工作状态，消除结构非弹性变形。具体是让4辆30 t的载重车，缓慢在往返桥上通过2次。静载和动载试验的测试断面及测点布置分别见图4和图5。

1.3.2.1 工况1、2

a）测试项目 加载车中载、偏载两种工况下，跨中附近S1断面处拱肋最大正弯矩的加载试验。

b）测试内容 测试跨中附近S1、S5断面处各测点的应力和挠度变化，并测定跨中附近7号、8号和9号吊索的索力。

1.3.2.2 工况3、4

a）测试项目 加载车中载、偏载两工况下拱肋L/4断面S2最大正弯矩，同时也是拱肋3L/4断面S3达到最大负弯矩的加载试验。

b）测试内容 测试 S1、S5、S2、S4、S3、S6 断面处测点的应力与S2、S4、S3、S6断面测点的挠度值。

1.3.2.3 工况5、6

a）测试项目 加载车偏载、中载两工况下拱肋L/4处S2断面最大负弯矩同时也是拱肋3L/4处S3断面达到最大正弯矩的加载试验。

b）测试内容 测试 S1、S5、S2、S4、S3、S6 断面处测点的应力与S2、S4、S3、S6断面测点的挠度值。

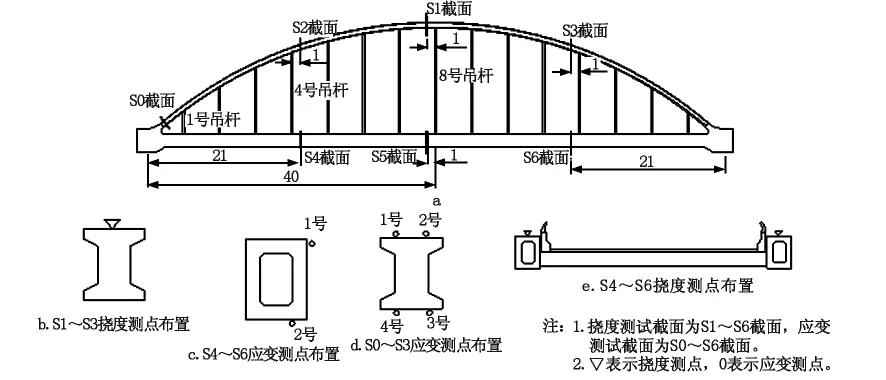
图4 静载测试断面及测点布置图（单位：m）

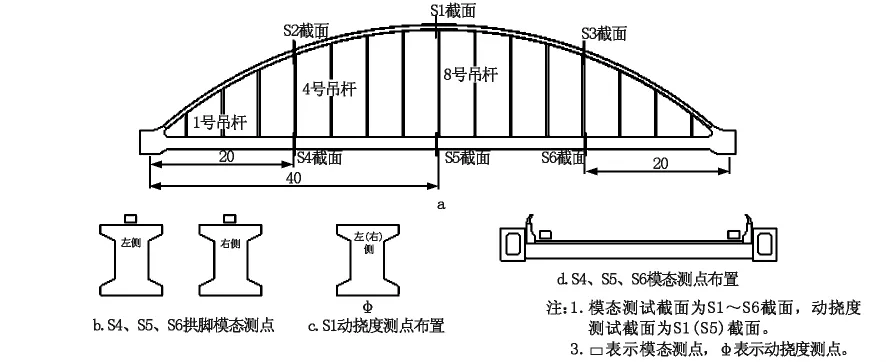
图5 动载测试断面及测点布置图（单位：m）

1.4 静载试验结果及分析

1.4.1 索力测试结果

基于索力测试的振动学原理，吊杆索力只与它的单位长度质量、长度、弯曲刚度、自振频率以及自振频率的阶数有关，它对于满足边界条件的受张拉的索都是适用的。只要精确地测出它的自振频率，代入准确的索长、单位长索重和弯曲刚度，就可以比较精确地计算出它的索力。

在拱肋L/2最大正弯矩工况暨8号吊杆最大索力工况（工况1、2）下，测试了跨中部分吊杆的索力增量。

吊杆索力测试表明，成桥状态吊杆索力均达到10%的误差要求，索力张拉达到了预期的效果。吊杆在恒载、活载作用下的索力满足设计要求。

1.4.2 应力测试结果

各工况下，各测试截面的应变实测值，按照混凝土弹性模量Eh=3.45×104MPa换算成混凝土应力。偏载工况的应力理论值，考虑了在两车偏载下由杠杆原理计算得出的横向分布系数。

各中载工况下（工况 1、3、5），左右两侧拱肋的应变校验系数大致相等，表明在对称荷载作用下结构受力对称性良好。应变校验系数在0.55～0.65之间属于预应力结构的常值范围。各偏载工况下（工况2、4、6），汽车靠近南侧拱肋偏心布置，南侧拱肋的校验系数相对小，北侧拱肋的校验系数相对较大，可以看出结构的偏载作用比设计要小，荷载横向分布较均匀。

1.4.3 挠度测试结果

根据理论计算，当按照工况1、工况2加载时，桥跨L/4、3L/4附近结构位移数值小。按照工况3、工况4、工况5、工况6加载时，桥跨跨中附近结构位移数值小。这些情况下位移量小的截面挠度值并不关心，可不予测量。

对于预应力混凝土结构：应变校验系数在0.6≤η＝S实测/S理论≤0.9，挠度校验系数在0.7≤η＝S实测/S理论≤1.0范围内属于常值范围，校验系数略小，表明结构具有较好的安全储备。

由分析结果可知，各工况下应变、挠度的校验系数平均值均满足要求，且在常值范围内，说明测试桥跨实际刚度要高于理论分析所采用的刚度，结构各主要受力部位在试验荷载作用下工作性能良好，安全性、经济性较好。

1.4.4 偏载增大系数

横向偏载系数反应了结构在汽车偏载作用下，某侧拱肋截面的内力增大情况。偏载增大系数越小，表明结构横向联系越可靠，横向分布越均匀。对于双肋拱桥，两个四分点之间采用刚性横梁法计算，支点采用杠杆法计算，支点与四分点之间直线内插计算，两列车偏载作用下支点的偏载系数为1.383，跨中的偏载系数为1.425，汽车跨中偏载作用时，横向增大系数跟理论计算值非常接近，在L/4及3L/4偏载时，偏载系数均小于理论值，表明按照此方法计算的双肋拱桥横向分布精度较高，同时该桥的横向联系可靠。

2 动载试验

动载试验主要用于了解桥梁自身的动力特性和抵抗受迫振动（行车）和突发荷载（跳车、制动）的能力。

动载试验主要包括两个方面的测试。一是进行模态试验以测定结构的振型、频率、阻尼比等模态参数；二是通过行车试验测定桥梁的冲击系数。

2.1 模态试验

桥梁结构在接近白噪声的震源影响下，会产生随机振动，利用测得桥上的这种微小随机响应信号，通过频谱分析得出该桥的自振频率（固有频率）、阻尼比和振型等。利用环境激励法试验来测试结构的动力特性已经被多次证明是适应于大型较低频结构的一种好方法。

测点拾振器布置一般按照结构振型形状，在变位较大的部位布置测点，尽可能避开各阶振型的节点。采集各测点时域波形图，通过传函分析和模态拟合，分析出振动模态参数，包括振动频率、阻尼比和振型。

2.1.1 结构振型

建立拱桥的空间有限元模型，能较为准确地分析出该结构的振动模态参数。

桥梁在外界荷载等因素的作用下，主要激发出第一阶振型。所以对一般结构更强调测试一阶振型来把握结构的动力性能。实测得到的一阶振型与理论计算振型吻合良好。

2.1.2 基频与阻尼比

测试结构特征频率和阻尼比可以反应结构的整体工作状况和损失程度。振动频率和阻尼值如表1所示，fmi/fdi＞1，表明结构有良好的动刚度，整体性能好。阻尼比为2.96%，属于预应力混凝土结构的常值范围，表明桥跨结构振动正常。

表1 自振特性实测值与理论计算值

2.2 行车试验

2.2.1 结构时程曲线

让一辆载重约30 t的主车，以速度20 km/h、30 km/h、40 km/h和50 km/h的速度匀速通过桥跨结构，测试该拱桥跨中截面竖向的动挠度时程响应曲线。

本次车辆激励试验采用一辆30 t的载重车，根据试验方案，本次车辆激励试验按照表2中的工况进行。车辆激励试验时动挠度时程响应测点选取响应最大的中跨跨中。限于篇幅，仅给出50 km/h匀速跑车的跨中挠度时程曲线，见图6。

表2 车辆激励试验工况表

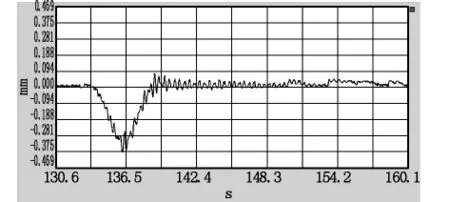
图6 50 km/h行车跨中挠度时程曲线

2.2.2 实测冲击系数

活载冲击系数（不同速度下）可根据记录的动应变或动挠度曲线，进行分析整理而得，可按式（1）计算：

式中：Smax为动载作用下该测点最大应变（或挠度）值，即最大波峰值；Smean为相应的静载作用下该测点最大应变（或挠度）值（可取本次波形的振幅中心轨迹线的顶点值），Smean=1/2(Smax+Smin)。其中Smin为与Smean相应的最小应变（或挠度）值（即同周期的波谷值）。

通过对桥梁在不同车速下的时间历程曲线进行分析整理而得，各行车速度下的桥梁实测冲击系数见表3。

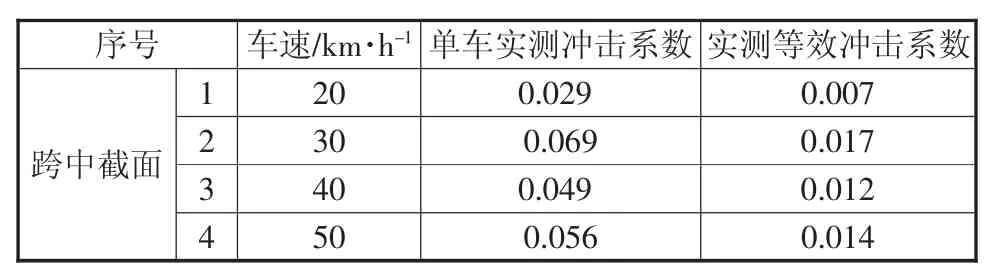
表3 实测冲击系数

单车试验的动力系数比汽车车列试验的冲击系数大，应采用与设计荷载相当的试验荷载所引起的冲击系数，作为理论冲击系数比较的依据。此动载试验效率系数ηd=0.25，根据《大跨径混凝土桥梁的试验方法》中动力试验结果的评定方法，换算后得到等效于设计荷载的冲击系数。

桥梁理论冲击系数根据现行设计规范当结构基频f＜1.5 Hz时，理论冲击系数μ=0.05，可见实测冲击系数μ小于理论值，桥梁行车性能良好。

3 结论

a）静载试验荷载的效率系数值在规定0.80～1.05范围内，吊杆在恒载、活载作用下的索力满足设计要求，结构残余变形较小，结构处于弹性受力状态，桥梁强度满足设计要求，桥梁结构刚度满足设计要求。

b）动载试验所采用的测试方法可行，测试结果可靠，结构整体刚度较高，结构各部件整体性能和技术状况良好，桥面平整度与桥梁行车性能良好。

c）桥梁技术状况良好，结构达到设计荷载公路-Ⅱ级的承载力及刚度要求。