月牙肋岔管三维参数化设计方法研究

张 伟，齐一鹤，刘姝麟，3，杨绿峰，4

(1.广西大学 土木建筑工程学院，广西 南宁530004;2.广西防灾减灾与工程安全重点实验室，广西 南宁530004;3.广西交通科学研究院，广西 南宁530007;4.广西壮族自治区住房和城乡建设厅，广西 南宁530028)

0 前 言

压力钢管是输水工程中重要的组成部分，且靠近厂房，因此其安全性和经济性一直受到工程和科学研究者的重视［1-3］。长距离输水工程常采用集中供水或分组供水方式，岔管是处于这两类输水管道的“咽喉”位置。目前，岔管结构型式主要有三梁、月牙肋、贴边、无梁和球形等类型，其中月牙肋岔管是在三梁岔管基础上发展起来的一种结构型式，由于具有结构型式简单、受力合理和制作安装难度较低等优点，在国内外大中型抽水蓄能等电站中得到广泛的应用［4-7］，已积累了较多工程实践经验。然而，由于月牙肋岔管分岔处支管将圆柱主管剖切开，使得膜应力为主的柱壳结构转化为存在显著局部应力的复杂受力体系，同时需考虑加强梁与壳体结构的联合承载机制，使得其设计及评价较复杂与繁琐［8-9］。因此，有必要开展该类岔管的高效参数化设计方法研究。

目前月牙肋岔管设计方法主要包括简化解析法和基于大型设计分析平台的方法。解析法方面，《水电站压力钢管规范》(SL 281-2003)根据空间解析几何和简化力学分析给出了月牙肋岔管的体型参数和结构尺寸的解析计算方法，该方法已成为目前岔管设计的基本方法，但直接应用时存在计算参数众多、设计过程繁琐和难以结构优化等不足［10-11］。为此，一些研究者提出了基于大型设计分析平台的方法:郑安兴等［12］提出了基于三维CAD 的设计方法，可应用于三梁岔管设计中;杜英奎等［13］开发了月牙肋岔管自动化设计系统，能够结合CAD 和有限元分析平台进行体形设计和结构分析;付山等［14］开发了基于CATIA 二次开发的辅助设计系统，可实现月牙肋钢岔管的快速建模和结构分析。基于大型设计分析平台的月牙肋岔管设计方法能克服传统简化解析法中存在的前述不足，已成为岔管结构设计方法研究中的热点方向［15-16］，然而现有方法仍存在初始设计方案不明确和结构计算模型不准确等问题［17］。

鉴于此，本文在此前研究成果基础上，系统地提出了一种月牙肋岔管的参数化设计方法，同时开展了月牙肋岔管结构响应的一些重要影响因素研究，给出了相关建议，为月牙肋岔管设计提供科学依据和高效方法。

1 参数化设计基本思路

结合FORTRAN 程序语言、CATIA 设计平台和有限元分析平台，采用有机结合的三个关键模块——初始设计方案形成模块;三维参数化设计模块;结构分析与优化模块，实现了月牙肋岔管三维参数设计。三维参数化设计基本思路为:首先采用FORTRAN 程序语言，依据《水电站压力钢管规范》(SL 281-2003)给出的月牙肋岔管体型参数和结构尺寸解析计算公式，编制了基于设计理论和经验参数计算程序，实现了结构初始设计方案的形成;然后接入CATIA 设计平台中，可进行参数化设计与调整，实现了三维参数化设计方案的形成;最后将得到的参数化设计模型导入有限元分析平台，对设计方案进行结构分析与优化，能提供满足安全和经济要求的最终结构设计方案。三维参数化设计流程如图1，fmax和［f］指膜应力区或局部应力区控制点的折算应力及其容许应力。

2 三维参数化设计方法

2.1 初始设计方案的形成

根据设计资料和《水电站压力钢管规范》(SL 281-2003)要求，拟定岔管的体型参数之后，采用FORTRAN 程序编制了月牙肋岔管初步设计程序，即包括输入文件、主程序和输出文件:输入文件读入给定的岔管结构基本资料;主程序进行明管和埋管的管壁厚度计算，以及根据肋板顶点位置和中央截面内力确定肋板尺寸;输出文件输出管壁厚度和肋板尺寸及其他三维参数化设计所需要的体型参数，完成初始设计方案。初始设计方案模块和三维参数化设计模块流程如图2。

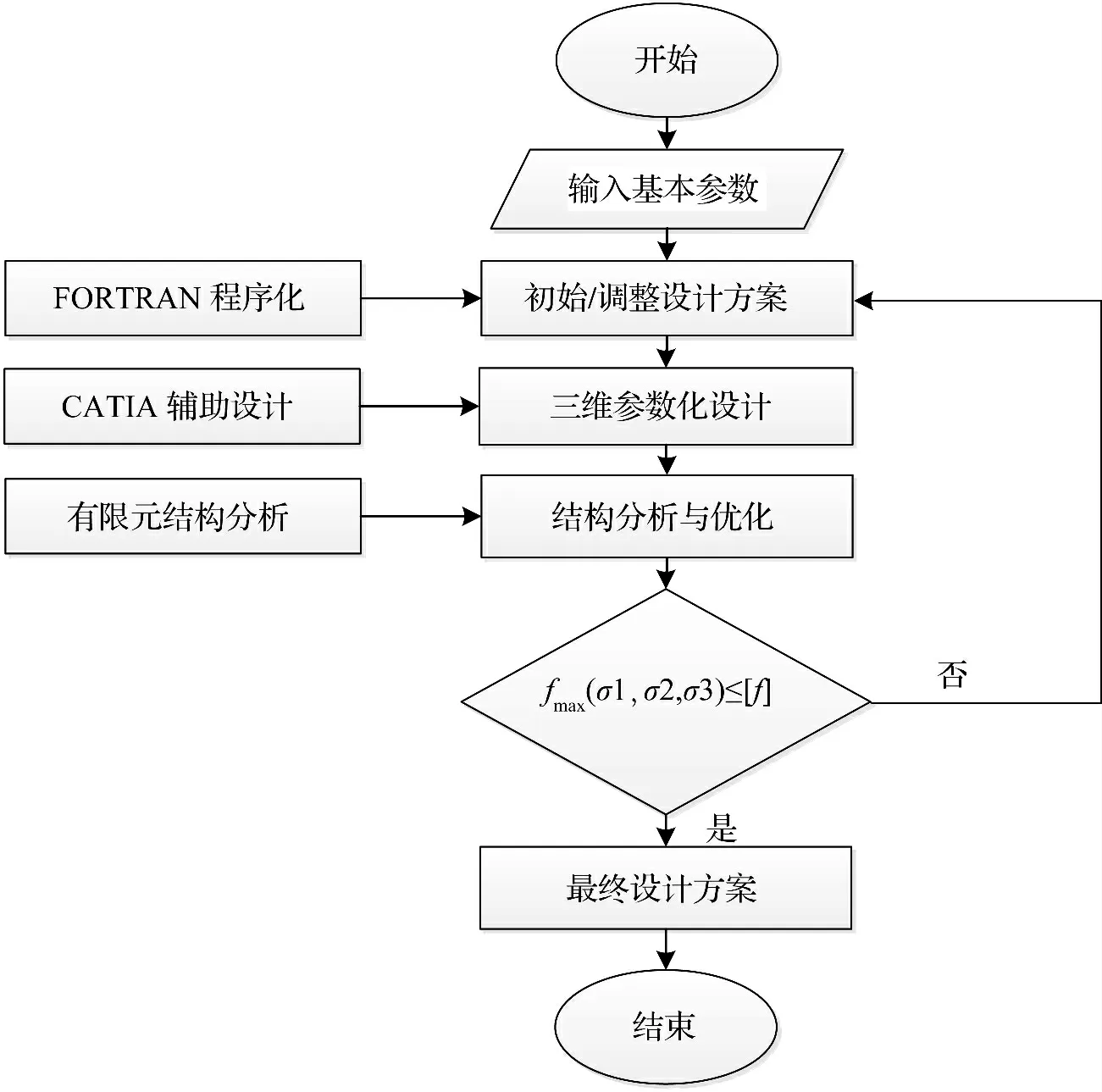
图1 三维参数化设计流程图Fig.1 Flow chart of the 3D parametric design

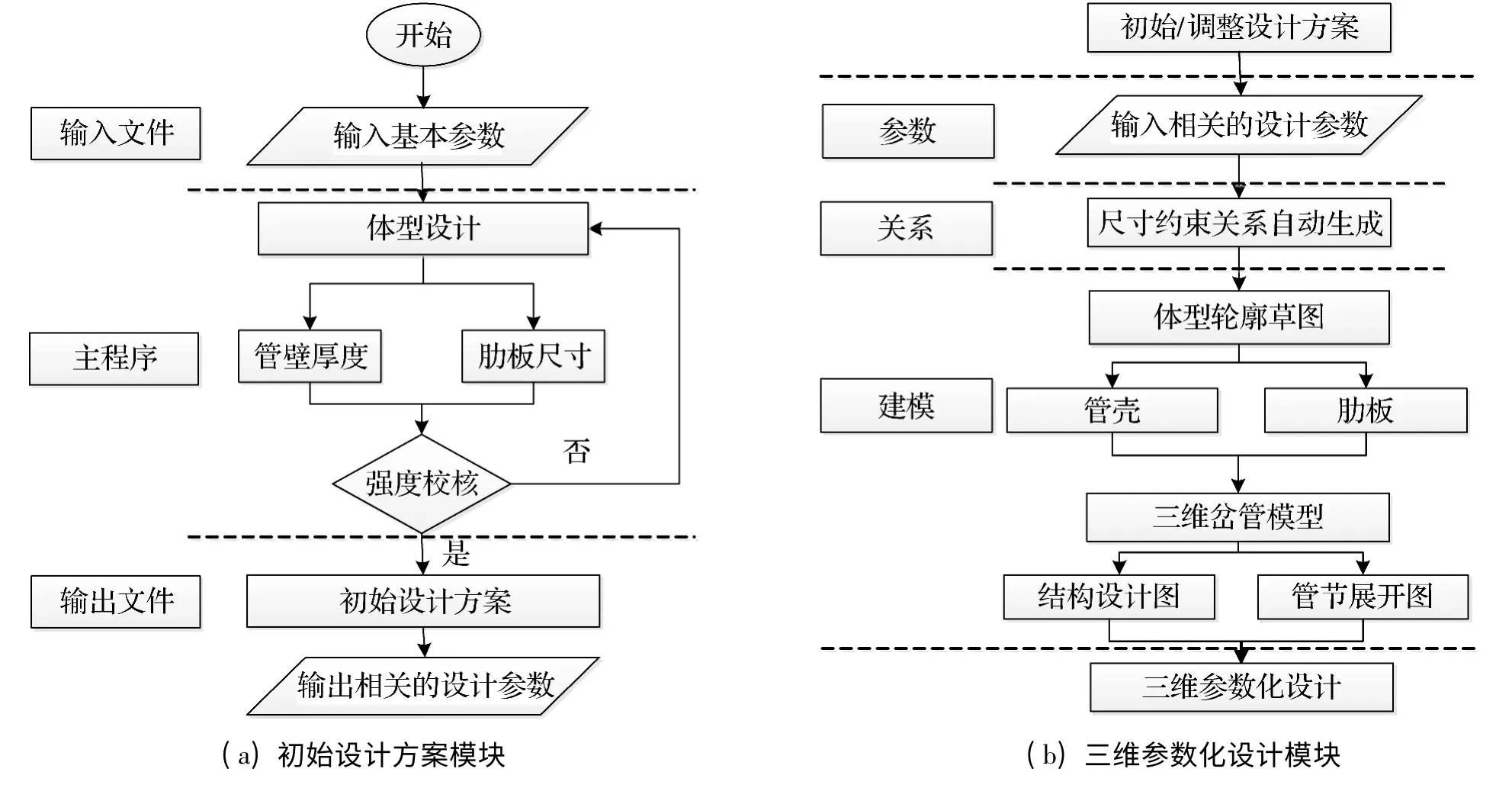
图2 初始设计方案和三维参数化设计模块流程图Fig.2 Flow chartof preliminary scheme and 3D parametric scheme modules

2.1.1 岔管的体型参数

初始设计方案的管壁厚度t0可按照应力分类法估算，根据膜应力区和局部应力区的安全性要求，按式(1)计算:

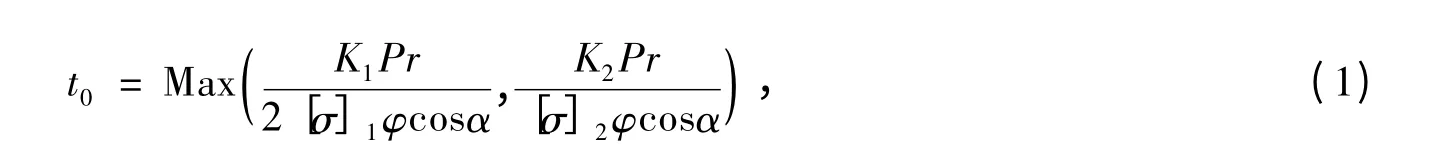
式中，P 为内水压力;r 为该节钢管最大内半径;α 为钢管半锥顶角;φ 为焊缝系数;［σ］1和［σ］2分别为岔管膜应力区和局部应力区的允许应力;K1和K2分别为岔管膜应力区和局部应力区的应力计算系数。

月牙肋岔管体形参数示意如图3(a)和图3(b)，各参数可根据空间几何关系由一些初步设计参数确定。初步的体型参数包括公切球半径R;分岔角ω;各锥管的半锥顶角α1、α2和α3;各锥管进出口半径R1、R2和R3。由此，可以得出参数包括腰线转折角θ12和θ13;本体三个锥管沿腰线的节距S12、S13和S23;分岔角ω12和ω13;各锥管节轴线长A1、A2和A3。

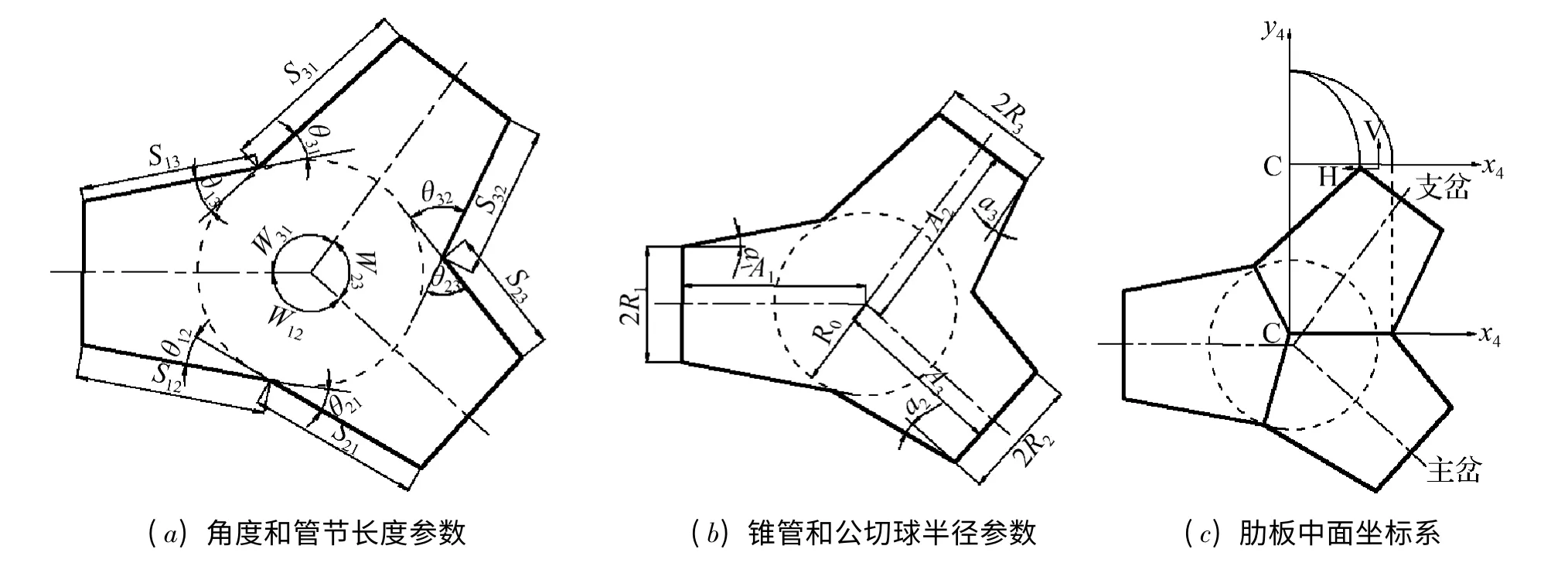
图3 月牙肋岔管体形参数与肋板中面坐标系Fig.3 Geometric parameters and coordinate system for rib middle surface

2.1.2 肋板尺寸参数

在如图3(c)肋板平面参考系中，可得肋板中面与主、支岔中面相交曲线上各点的坐标值，各坐标值如下式，进而可得管壁相贯线曲线，肋板外缘曲线可根据相贯线适当留余幅后确定。

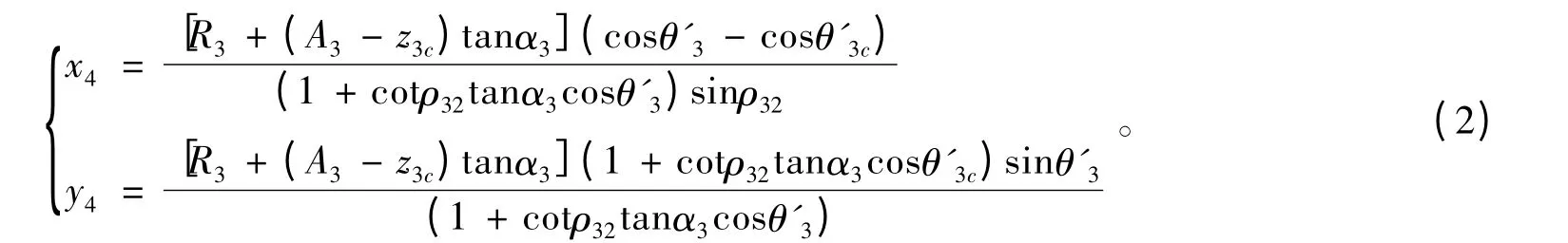
肋板厚度按下式

式中，C 为壁厚裕量;BT为肋中央断面宽度;［σ］1为允许应力;V 为主岔锥作用于肋板中央截面上的垂直分力。

2.2 参数化设计

将初始设计方案导入CATIA，获得基于CATIA 的三维参数化模型，该模型主要包括三个部分:①参数，即用户自定义的参数，可根据经验或优化要求驱动参数变化，实现三维参数化调整;②关系，即各尺寸约束之间的数学关系，在绘图过程中自动生成;③零部件几何体，就是建立的三维模型，包括草图建立、管壳和肋板形成。

月牙肋岔管参数化模型的建立分为三个步骤:首先做出模型的草图，即模型基本轮廓;然后基于草图基本轮廓利用旋转、拉伸和分割等命令得出管壳部分;利用切割出来的相贯线定义肋板平面，在该平面中通过偏移等命令得出肋板。获得三维设计方案后，可进一步进行结构设计图和管节展开图等输出，三维参数化设计模块流程如图2(b)。

2.3 结构分析与优化

将CATIA 中建立的三维几何模型导入有限元结构分析平台中，本文采用大型商用有限元软件ANSYS 进行结构分析:首先对三维几何模型进行有限元结构分析前处理，包括定义单元类型、板壳厚度和材料参数，进行网格剖分，施加荷载作用和约束条件;然后进行结构分析，得出各控制区域的计算内力和应力;进而结合规范进行结构安全评定:

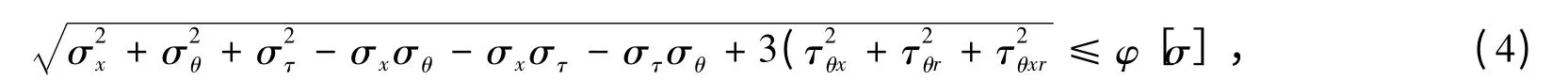
对肋板等可简化为平面问题的构件进行结构分析时，可采用式(5):

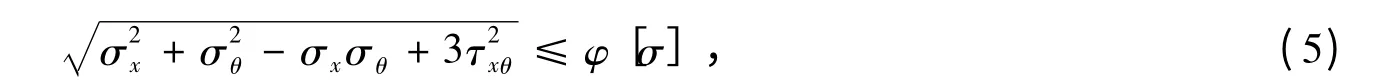
式中，σx、σθ和στ分别为轴向、环向和径向正应力;τθx、τθr和τxr为各向剪应力;φ 为焊缝系数;［σ］为相应计算工况的允许应力。

采用式(4)和式(5)评估设计方案不满足安全性要求时，则需通过调整结构体型、增大结构厚度或提高材料强度等方法获得新的设计方案，再次根据图1 三维参数化设计流程进行结构设计与分析，直到满足安全性要求。同时，若设计方案满足安全性要求，但有较大安全储备时，也根据相同流程，通过调整结构体型、减小结构厚度等方法获得更为经济的优化设计方案。

3 岔管参数化设计实例

3.1 参数化设计

某引水系统埋藏式钢岔管，材料参数见表1，主管、主岔管和支岔管内半径分别为2 100 mm、1 800 mm和1 300 mm，公切球半径为2 300 mm，半锥顶角分别为12°、10°和19°，分岔角为68°，采用本文图1 所示参数化设计流程进行结构设计，将已知设计参数输入采用FORTRAN 程序编制的月牙肋岔管初步设计程序中，得到了符合规范要求的岔管体型参数，并得到了初始设计方案，其基本设计参数见表2，体型如图4。

表1 岔管材料参数Tab.1 Material parameters of the branch pipe

表2 基本设计参数Tab.2 Preliminary design parameters

3.2 结构计算模型

3.2.1 模型与网格

将岔管模型导入ANSYS 程序中进行结构分析，根据结构和荷载对称性取一半模型进行分析，采用SHELL281 单元，对称面施加对称约束。根据应力分类法确定岔管的应力控制点与ANSYS 中网格划分如图5。

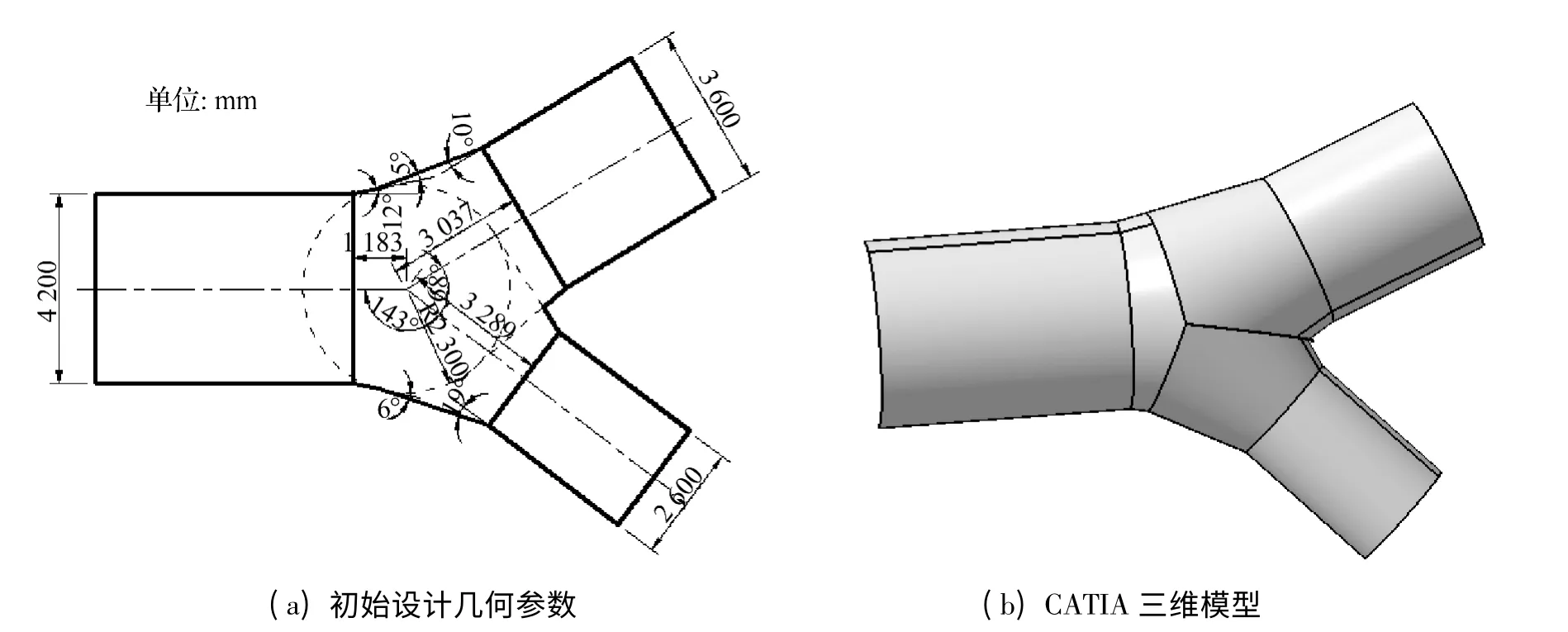
图4 初始设计几何参数和三维模型Fig.4 Geometric parameters and 3D model in CATIA

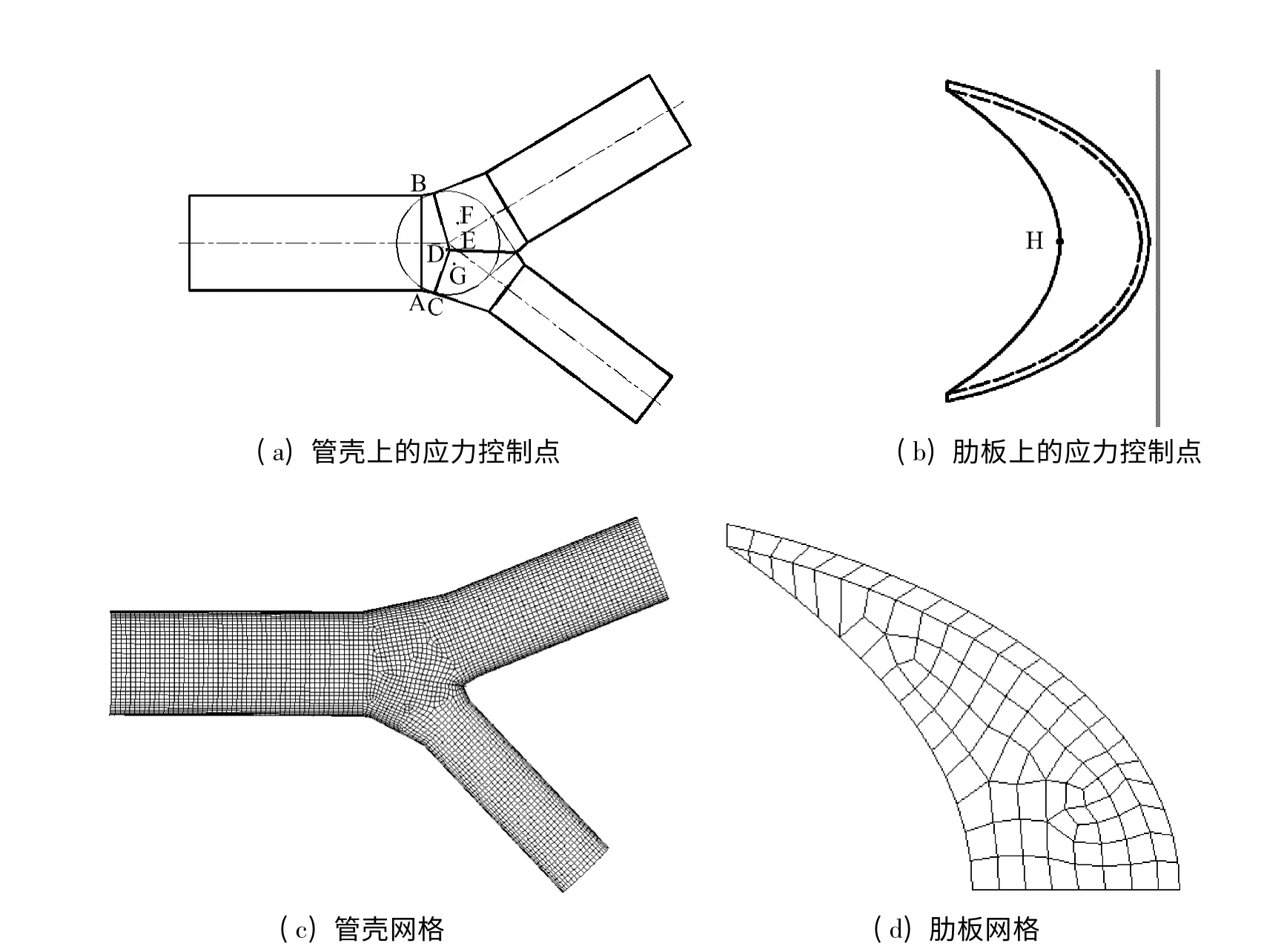
图5 岔管应力控制点和有限元模型Fig.5 Controlled region and finite element model of the branch pipe

3.2.2 模型范围与约束条件的影响

模型范围与约束条件是结构计算模型的基本要素，合理设置这两个要素是结构响应分析计算结果有效性的基本保障。岔管受力复杂，结构响应受计算模型和约束条件影响显著，然而现《水电站压力钢管规范》(SL 281-2003)和研究工作都未对这两个要素给出明确建议［12］，为此有必要研究给出科学建议。文中对岔管端部分别取轴向约束和固端约束，并将模型范围取为公切球半径R0的2 ～8 倍，进行结构分析，模型范围和约束条件对控制点应力的影响如图6 所示。

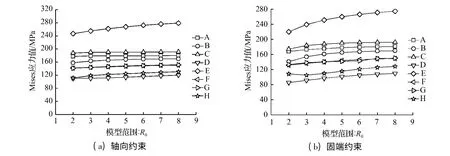
图6 模型范围和约束条件对控制点应力的影响Fig.6 Influence of model range and constrain condition on stress distribution in controlled region

由图6 可见，两种约束下控制点应力与模型范围的变化规律基本一致，均随模型范围的增大而增大，且模型范围达到5R0时，计算结果基本稳定。同时可见，相对固端约束而言，轴向约束下的应力计算结果更易在较小模型范围内稳定，两种约束条件在模型范围达到5R0时，计算结果趋于一致。因此，偏于安全性角度考虑，建议月牙肋岔管结构分析时，岔管端部考虑取轴向约束，模型范围考虑取5R0以上。

3.3 结构响应影响因素分析

3.3.1 分岔角对结构响应的影响

分岔角是影响月牙肋岔管结构响应的重要因素，文中取岔管端部轴向约束，取模型范围:公切球半径R0=5，考虑分岔角在55°～90°，计算分析分岔角对岔管结构应力的影响，控制点应力和肋板中央截面最大位移随分岔角的变化规律如图7。

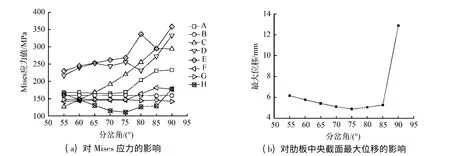
图7 分岔角对控制点应力和肋板中央截面最大位移的影响Fig.7 Influence of bifurcation angle on structural deformation and stress distribution in controlled region

由图7 可见，随着分岔角的增大，管壳局部应力与膜应力基本呈增大趋势，且在80°之后增大比较明显，同时分岔角达75°以上时肋板最大控制应力点将由中央截面转移到上下肢附近。岔管肋板中央截面最大位移，也是总位移最大处，随分岔角增加呈先减小后增大趋势，数值在55°～75°时最小。根据分析结果，综合考虑水力学要求以及分岔角对结构响应的影响，建议体型设计时分岔角取55°～75°。

3.3.2 肋板厚度对应力场的影响

肋板主要用于加大相贯线处的刚度，保持结构在设计荷载作用下处于小变形状态，因而将承受管道剖切所引起的较大不平衡力，导致其体型厚重。研究者们从设计与优化角度常关注肋板厚度对应力场的影响［18］，《水电站压力钢管规范》(SL 281-2003)中目前建议“肋厚不应小于管壁厚度的2 倍”。文中进行了计算分析，肋板厚度:管壁厚度对控制点应力的影响如图8所示。

由图8 可见，肋板厚度对管壁应力影响不大，但对肋板最大应力有一定影响，随肋板厚度的减小，肋板最大应力呈线性增长趋势。肋板应力达容许应力值时，肋板厚度与管壁厚度之比为1.67，可见从结构安全角度看，肋板厚度可低于管壁厚度的2 倍，本例可取至1.7，以获得更为优化的结构设计方案。

3.4 设计方案结构响应分析

根据岔管参数化设计方案，结构Mises 应力分布如图9，各工况下控制点计算应力与容许值如表3 所示。

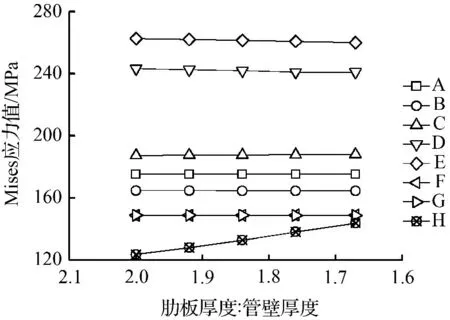
图8 肋板厚度对控制点应力的影响Fig.8 Influence of the thickness of crescent rib on stress distribution in controlled region

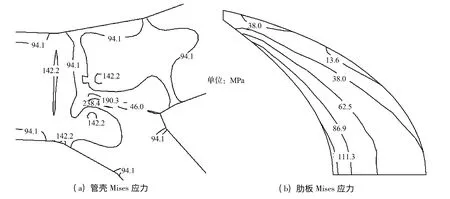
图9 结构的Mises 应力Fig.9 Mises stress in the branch pipe

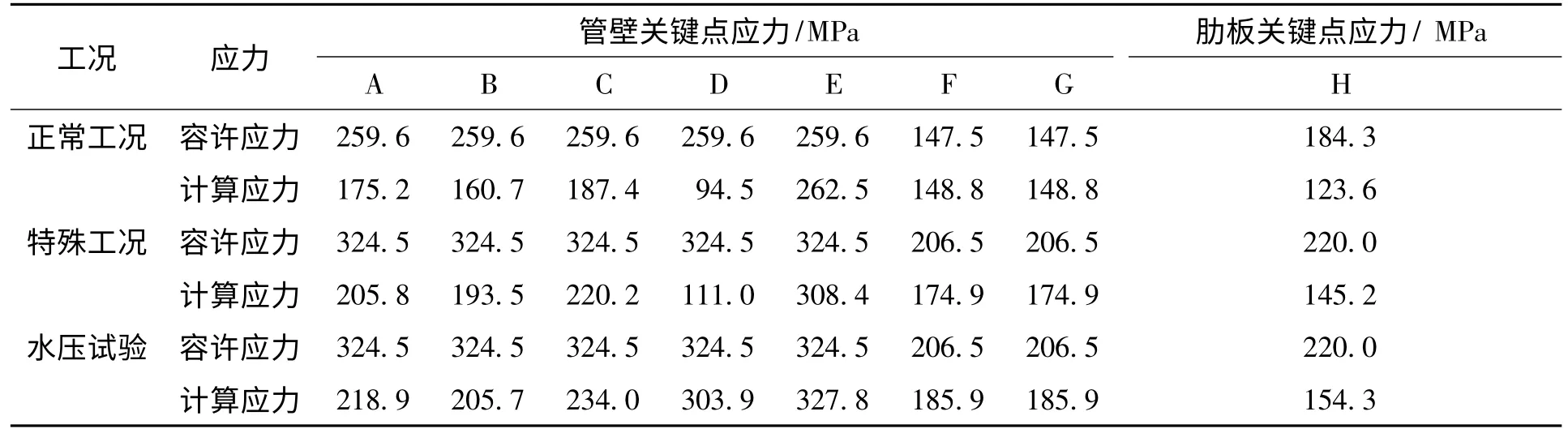
表3 控制点计算应力与允许值Tab.3 Calculated stresses and admissible stresses of the controlled region

可见，本岔管的主锥与主岔腰线转折角C 点、膜应力区F 点和G 点、肋板处H 点的应力值在各工况下都能满足容许应力限值的要求，并且控制点的应力值最大不超过容许应力值的1.12%，满足工程实际的要求。因而本方案可作为设计方案。

4 讨 论

4.1 三维参数化设计方法

月牙肋岔管设计方法目前主要有简化解析法和基于大型设计分析平台的方法。《水电站压力钢管规范》(SL 281-2003)中根据简化力学与空间几何的方法来计算月牙肋岔管体型参数以及结构尺寸，但是计算过程中需要计算的参数过多，设计过程繁琐。因此，基于大型设计分析平台的方法应用广泛，解决了传统月牙肋岔管设计方法的不足，但同时存在着初始方案不明确等问题，为此本文提出了一种结合FORTRAN 程序语言、CATIA 结构设计平台和有限元结构分析平台的月牙肋岔管三维参数化设计方法，克服了现有基于大型设计分析平台方法的不足，可高效地进行岔管设计与优化。

4.2 结构响应因素及建议

现有月牙肋岔管设计方法未明确给出月牙肋岔管计算模型的模型范围与约束条件，同时《水电站压力钢管规范》(SL 281-2003)对月牙肋岔管给出了较宽泛的分岔角和肋板厚度建议。鉴于此，本文在三维参数化设计方法的基础上，以提高结构响应计算精度和给出良好承载性能的岔管结构为目标，开展了相关重要影响因素研究，并给出以下建议:结构分析中主管、支管端部均可取轴向约束，计算模型范围需取5 倍公切球半径以上，分岔角可取75°～80°，肋板厚度可取管壁厚度2 倍以下。

5 结 论

文中提出了一种结合FORTRAN 程序语言、CATIA 结构设计平台和有限元结构分析平台的月牙肋岔管三维参数化设计方法，可高效地进行岔管设计与优化。基于文中的月牙肋岔管的三维参数化设计方法，开展了月牙肋岔管计算模型和结构响应的影响因素分析，考虑结构安全性和经济性要求，建议月牙肋岔管结构分析中端部取轴向约束，计算模型范围需取5 倍公切球半径以上，岔管分岔角可取75°～80°，肋板厚度可取低于管壁厚度的2 倍以下。

［1］ KOZINETS G L，POTEKHIN L P.Numerical evaluating strength reliability of penstocks under hydraulic hammer［J］.Magazine of Civil Engineering，2012，32(6):29-35.

［2］ 张仲卿，梁政，魏有健.三峡水电站钢衬钢筋砼压力管道承载能力研究［J］.广西大学学报:自然科学版，1998，23(4):303-308.

［3］ CHEN Z，ZHU W，DI Q，et al.Prediction of burst pressure of pipes with geometric eccentricity［J］.Journal of Pressure Vessel Technology，2015，137(6):1-8.

［4］ 赵云德，姚秀全.吉林台一级水电站大型高强钢月牙肋岔管制造安装技术［J］.水力发电，2006，32(6):52-54.

［5］ 王志国，陈永兴.西龙池抽水蓄能电站内加强月牙肋岔管围岩分担内水压力设计［J］.水力发电学报，2006，25(6):61-66.

［6］ 方子帆，吴德新，肖华攀，等.抽水蓄能电站月牙肋岔管设计与分析［J］.三峡大学学报:自然科学版，2012，34(6):73-76.

［7］ YANG L F，ZHANG W，YU B，et al.Safety evaluation of branch pipe in hydropower station using elastic modulus reduction method［J］.Journal of Pressure Vessel Technology，2012，134(4):1-7.

［8］ 张伟，杨绿峰，韩晓凤.基于弹性模量缩减法的钢岔管安全评价［J］.水力发电学报，2010，29(1):176-184.

［9］ 刘姝麟.月牙肋岔管的三维参数化设计与安全评估［D］.南宁:广西大学土木与建筑工程学院，2013.

［10］吴启煌.钢岔管展开图的数解法［J］.水力发电，2003，29(7):49-51.

［11］宋蕊香，伍鹤皋，苏凯.月牙肋岔管管节展开程序开发与应用研究［J］.人民长江，2009，40(13):34-37.

［12］郑安兴，武亮，徐天宝.基于三维CAD 技术的水电站压力岔管设计方法［J］.水电能源科学，2010，28(1):124-126.

［13］杜英奎，蒋逵超，王春江，等.月牙肋钢岔管自动化设计系统开发与应用［J］.水力发电，2011，37(8):56-58.

［14］付山，伍鹤皋，汪洋.基于CATIA 二次开发的月牙肋钢岔管辅助设计系统开发与应用［J］.水力发电，2013，39(7):73-76.

［15］张伟，杨绿峰，韩晓凤.基于弹性补偿有限元法的无梁岔管安全评价［J］.水利学报，2009，40(10):1175-1183.

［16］付传雄，张伟，张瑾.基于弹性模量缩减法的钢衬钢筋混凝土压力管道极限承载力计算［J］.水利水电科技进展，2014，34(2):26-30.

［17］杜芳琴，伍鹤皋，石长征.月牙肋钢岔管设计中若干问题的探讨［J］.水电能源科学，2012，30(8):129-131.

［18］谢冠峰，李火坤.高水头卜型月牙肋岔管结构三维应力分析［J］.南昌大学学报:工科版，2009，31(1):90-95.