缆吊系统主扣合一塔架结构分析与优化

青志刚，罗小斌

(广西大学 土木建筑工程学院，广西 南宁530004)

0 引 言

缆吊吊装系统具有跨越能力大、适应性强等特点，广泛应用于大跨径拱桥的施工［1］。施工中，为了减少吊装过程主塔架偏位对已扣挂拱肋节段高程的影响，将主塔与扣塔分开设置，如广西那莫大桥、三岸邕江大桥、钦州钦江大桥等;塔架采用N 型万能杆件搭设，采用MIDAS/Civil 有限元分析软件进行验算［2］。湖南猛洞河大桥同样采用主塔、扣塔分离式布置，扣塔采用钢管格构柱搭设，基于强度理论进行计算，有限元软件建模验算［3］。实践表明，主扣塔分离式很好解决了拱肋节段吊装就位时已装拱肋高程的影响，但需要系统占地面积大，且塔架用钢量大，经济性不高。2013 年6 月建成通车的世界第一跨四川合江长桥一桥，采用吊塔置于扣塔顶部的方式，吊塔塔脚为铰接，扣塔脚为固结［1-3］。该方法部分解决了扣塔与主塔分离设置时占地面积大的问题，但需增加缆风数量确保主塔传递给扣塔的水平力是微小的，增加扣塔的用钢量、增大截面积提高整体抗弯刚度控制塔顶位移。显然，在复杂地质条件下无法进行主塔与扣塔的分离设计，在经济性要求下采用吊扣合一两者铰接相连的方式仍不理想。因此，笔者提出在扣塔上直接加高设置吊塔，布置一套缆风系统，实现真正的主扣合一塔架设置方式。通过分析主扣合一塔架的设计、分析可知，结构时安全的;并引入遗传算法对主扣合一塔架进行优化设计，效果是显著的。

1 遗传算法

遗传算法(Genetic Algorithm)就是一种搜索算法，它由美国的J.Holland 教授1975 年首先提出，主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法，能自动获取和指导优化的搜索空间，只适应地调整搜索方向，不需要特定的规则［4］。基本的遗传算法由染色体编码、适应度评价、遗传算子和运行参数四大要素组成。

①染色体编码

遗传算法不能直接处理问题的空间参数，必须把空间参数转换成遗传空间的由基因按一定结构组成染色体。最常用的编码方法是二进制编码，它由二进制字符集{0，1}所组成。

②适应度评价

适应度在进化论中表示某一个个体在环境中的适应能力，遗传算法中引入适应度函数，用于评定各个个体的优劣程度，适应度越大，则被选择遗传到下一代的概率越高。

③遗传算子

遗传算子有三种，分别是选择算子、交叉算子和变异算子［5］。选择算子把当前群体中适应度较高的个体按照选择函数遗传到下一代种群中，适应度值低的个体趋向于被淘汰，种群的平均适应度得到提高。交叉算子以某一概率将选择算子选择出来的个体两两之间的部分染色体进行交换，使个体的适应度相应地提高。变异算子进一步将个体中的小部分基因按某一较小的概率进行改变，产生实现种群的多样性，扩大搜索空间［5］。

④运行参数

遗传算法的基本运行参数有群体的大小M，遗传运算的终止进化代数T，交叉概率Pc，变异概率Pm。实际应用中，需要经过多次试算后才能确定出这些参数合理的取值大小或取值范围［4-5］。

2 主扣合一塔架结构分析

2.1 塔架布设

那厘右江特大桥主桥为160 m 上承式钢筋混凝土箱型拱桥，采用斜拉扣挂缆吊装技术悬臂拼装。桥址区为石芽、残丘等岩溶发育区，属河流冲积地貌。左岸岸坡基岩裸露，坡度较陡，近直立，自然斜坡稳定;拱座附近为残丘地带，有熔岩发育，高差约4 m;距离南百二级路190 m，中间为岩溶峰丛洼地地锚。右岸岸坡较缓，上覆1.5 ～3 m 的冲洪积粘土，下为断层角砾岩，为强烈挤压破碎区，在自然状态下斜坡能保持稳定;拱座41 m 范围内为强烈挤压破碎区，距离60、120 m 分别为两条断裂带［6］。通过“5H”确定吊塔架的高度为76 m，主承重索尾索的合理水平夹角取值范围α∈(18°～25°)，得出主地锚的布置区域为距塔架158 ～216 m，左岸与覆盖二级路，右岸有破碎区(承载力不足)、断裂带。受地形地质限制无法布置分离式主、扣塔，因此提出采取主扣塔合一的布置方式，见图1。

图1 大桥缆吊系统布置图Fig.1 Bridge cable system layout

2.2 塔架结构分析

主扣合一塔架采用N 型万能杆件搭设，塔架底部铰接;两侧柱头截面为4 m×4 m，中间为2 m×4 m;设置三道横梁，底、中横梁处安装滑轮式扣索鞍，顶横梁为缆吊系统横移轨道;缆风系统的布置情况为:底、中横梁纵桥向分别对称布置4 组，横桥向布置2 组，顶横梁纵桥向两端对称布置12 组，中部仅尾索方向布置2 根，横桥向对称布置2 组;钢丝绳均采用Φ28 钢丝绳，每根绳施加50 kN 的预拉力(图2)。最不利荷载工况为:吊装边箱、扣挂3 个节段、第四节段起吊及移动至安装位置，见表1。

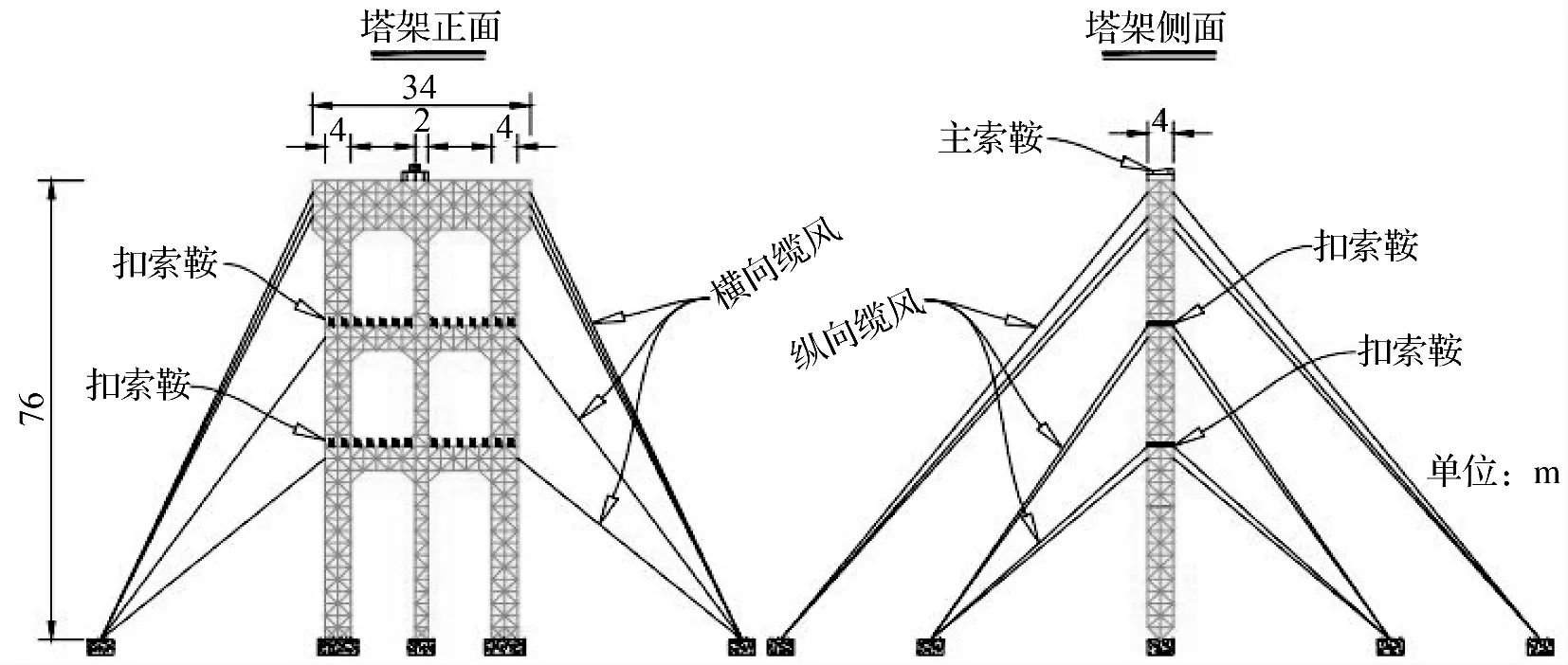
图2 缆风系统布置图Fig.2 Wind cable system layout

表1 最不利荷载工况1Tab.1 The most unfavorable load case

在Midas Civil 通用有限元软件中建立三维计算模型，立杆采用梁单元，其余杆件采用桁架单元［7］;缆风绳为纤维芯钢丝绳，在软件中合理模拟其性能比较困难，采用仅受拉的弹性支撑进行替代［8］;塔底铰接，限制三个方向的位移和横向、竖向的转动，模型约束情况见图3。验算荷载情况为:吊装荷载85 t，分别扣挂3 段外边箱(最不利工况)、中箱、内边箱时的水平分力及竖向分力，受5 级横向、纵向风载。杆件截面及最大应力情况表2。

表2 杆件截面及最大应力表Tab.2 Section and maximum stress table of member

从表2 可见，水平杆均存在应力超限情况，超限杆件均为扣索鞍下水平杆，模拟计算时采用的是2N4，未考虑扣索鞍安装时更换成2［25a 槽钢的情况，经过独立计算，更换后满足要求。

图3 模型图Fig.3 Model chart

3 遗传算法优化因素及过程

3.1 优化因素

对主扣合一塔架建立优化数学模型，主要包含设计变量、目标函数和约束条件3 个基本因素［9］。通过结构分析可知，塔架能满足各种工况要求，且确定结构形式，初拟了各部位杆件截面，未按照受力大小进行详细的优化。因此，对该结构的优化方向即按照各杆件的受力情况，选择合理的截面组合形式进行优化设计，求最小用钢量。现采用各杆件组合截面面积为设计变量:

以结构的总重量作为目标函数:

式(2)中，ri为杆件的比重，li为杆件的长度，n 为杆件的数量。

以各万能杆件的强度和稳定性作为约束条件［2］:

式中，Ai为各杆件的截面积;Ni为杆件的轴向力，从Midas/Civil 中导入;［σ］为杆件的容许应力:杆件间通过螺栓连接，不能按照材质强度控制杆件应力，取其修正容许应力(表3)［10］;λ 为杆件的长细比，［λ］为容许长细比，按钢结构设计规范(GB50017-2003)取值;N压为压杆的轴向力;φ 为轴心受压杆件稳定系数，按钢结构设计规范(GB50017-2003)取值。

表3 杆件修正容许应力Tab.3 Rod correction allowable stress

3.2 优化过程

N 型万能杆件主要由三种截面杆件组成，每种截面可以由1 ～4 根拼装成组合截面以适应不同荷载等级要求;杆件间通过特殊的节点板连接，立杆为∠120×120×10 mm 角钢，其余杆件为∠100×100×10 mm或∠75×75×8 mm 角钢。以上截面限制由万能杆件的特殊性所决定。在遗传算法中，仅需抓住主要矛盾进行优化，即忽略不同位置杆件类型限制，默认杆件截面由表4 中选取，优化过程如图4。

表4 杆件截面信息Tab.4 Information section bar

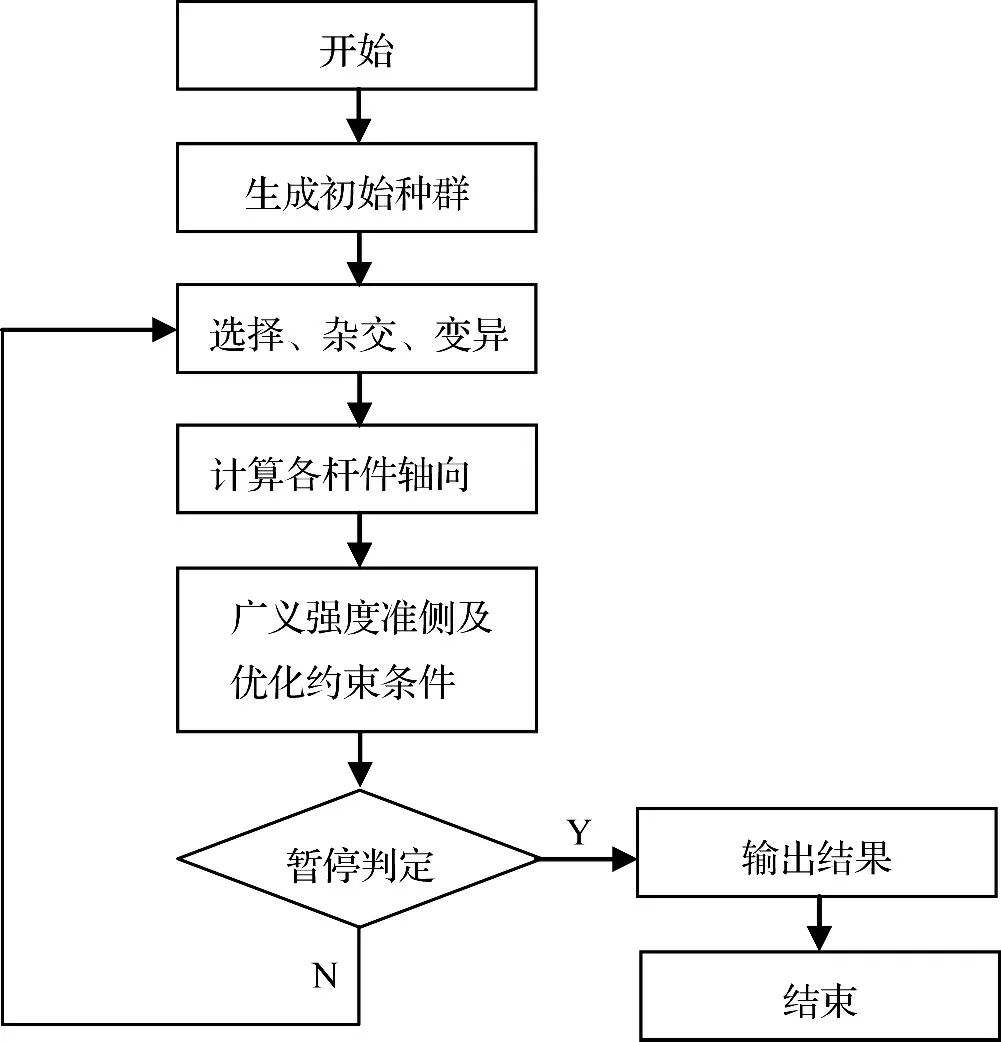
图4 优化过程图Fig.4 Optimization process chart

依据优化过程图，首先生成初始种群:主扣合一塔架共有杆件4 722 根(M=4 722)，通过随机方法产生100 个个体组成初始化种群。接着程序计算初始化种群的适应度，个体适应度越高，该个体被遗传的概率越高，反之越低［11］。为正确计算不同情况下各个个体的遗传概率，要求所有个体的适应度必须为正数或零，因此需引入变换式;由式(2)可知目标函数为求最小值的优化问题，采取式(6)的变换式:

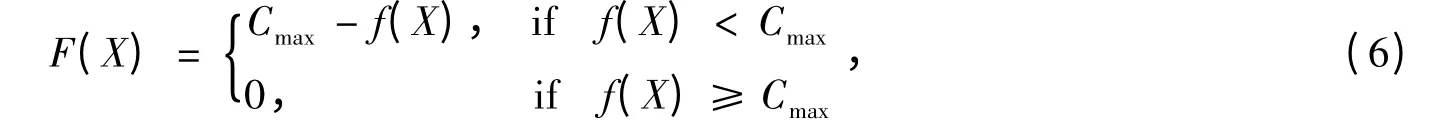
式中，F(X)为适应度函数，f(X)为目标函数，Cmax为一个种群进化到当前代为止最大的目标函数值。选择算子采用轮盘赌方法［5，9］，运行参数分别为:交叉概率Pc=0.8，变异概率Pm=0.001，终止代数T=500。

4 优化结果

将优化结果与常规方法设计塔架进行对比。常规方法塔架设计情况为:拟定塔架尺寸(与上文相同)，立杆采用4N1 铁，水平杆采用2N4 铁，横向斜腹杆采用2N5 铁，纵向斜腹杆采用2N3 铁，水平斜撑杆为2N5 铁，横梁斜腹杆均采用2N3 铁;采用Midas Civil 有限元软件进行强度、刚度、稳定性验算。将塔架采用遗传算法优化前、后的材料用量、杆件应力情况列于表5。

表5 塔架优化前材料用量Tab.5 Tower before optimization material consumption

表5 中累计重量为杆件重量，未包含连接杆件的节点板、拼接板、缀板、螺栓等部件。优化后的塔架中，立柱杆件部分杆件为4A2、4A3 截面，位于塔架上部，考虑万能杆件的固有连接特性，将这部分修正为2A1 截面。优化结果显示，N1/N2 杆件、N3 杆件显著减少，N4 基本保持不变，N5 明显增加;N1/N2减少的部分集中在横梁以上部分及底横梁直腹杆，由4A1 截面优化为2A1 截面，符合塔架底部受力大于顶部的特点;柱头纵向斜腹杆多数由2A2 截面优化为2A3 截面，横梁与柱头相交处为4A2，存在局部应力集中情况;塔脚未定型产品，不存在截面优化问题。N5 杆件最大应力值较优化前提高17.3 MPa，因优化前后截面积差值较大;其余杆件杆件应力变化不明显。经优化后，塔架杆件重量减少18%，取得了理想的效果。

5 结 语

经实践证明，在复杂地质环境中设置主扣合一塔架方案，顺利完成了那厘右江特大桥的安装工作，该方案可行;引入遗传算法优化程序，解决了主扣合一塔架受力复杂难以有效计算的难题，为该类优化问题提供借鉴;遗传算法优化万能杆件截面，节约用钢量，结果可靠。

［1］ 秦大燕，韩玉.500 m 级钢管混凝土拱桥安装技术研究［J］.西部交通科技，2014(7):26-30.

［2］ 黄金文，蒋严波.贵港郁江大桥缆吊吊装系统设计与创新［J］.中外公路，2013，33(4):195-200.

［3］ 汤伟，张鹏勃.斜拉扣挂法分离式扣挂系统在钢管拱桥的应用与浅析［J］.公路工程，2013，38(5):214-220.

［4］ 周明，孙树栋.遗传算法原理及应用［M］.北京:国防工业出版社，1999.

［5］ WANG Long，WANG Tong-guang，LUO Yuan.Improved non-dominated sorting genetic algorithm(NSGA)-II in multi-objective optimization studies of wind turbine blades［J］.Applied Mathematics and Mechanics(English Edition)，2011，32(6):739-748.

［6］ 涂桂松.马山至平果高速公路两阶段施工图设计［M］.南宁:广西壮族自治区交通规划勘察设计研究，2011:1-9.

［7］ 赵朝阳，杨文爽.缆索吊装系统的受力分析算法与工作性能［J］.广西大学学报:自热科学版，2010，35(4):616-620.

［8］ 谢开仲，林海瑛，梁寿宗.钢管混凝土提篮拱损伤识别方法［J］.广西大学学报:自然科学版，2010，35(1):96-99.

［9］ CHENG Dong-xiu，WANG Shou-chun，SUN Ren-jin.Design of artificial neural networks using a genetic algorithm to predict saturates of vacuum gas oil［J］.Petroleum Science，2010(7):118-122.

［10］交通部第一公路工程总公司.桥涵(下册)［M］.北京:人民交通出版社，2000:917-922.

［11］ZHENG Yi-feng，CAO Yu，WANG Yuan-yuan.Linear monitoring for cast-in-place reinforced concrete arch bridge construction［J］.Global Geology，2012，15(2):145-150.