钢管再生混凝土柱轴压性能及承载力计算

陈宗平，何天瑀，徐金俊，刘 祥

(1.广西大学 土木建筑工程学院，广西 南宁530004;2.广西大学 工程防灾与结构安全教育部重点实验室，广西 南宁530004)

建筑材料尤其是混凝土用天然骨料的日益消耗已造成了骨料产地严重的环境负担，因此节约资源和保护环境逐渐成为土木工程领域的行业主旨。混凝土的再生利用，对于实现绿色建筑、环境保护以及社会的可持续发展均具有极为重要的现实意义［1］。作为影响再生混凝土力学性能和耐久性能的两大因素，即再生粗骨料中的微裂纹和原始水泥基体，是限制再生混凝土扩大应用的根源所在［2］。

钢管混凝土作为钢-混凝土组合结构的一种形式，因其高承载能力和良好的抗震性能已在国内外得到越来越广泛的应用。从本质上讲，利用外包的钢管可有效克服再生混凝土的部分缺陷，从而实现再生混凝土的扩大应用。对于钢管再生混凝土力学性能的研究，国内外学者已取得了大量研究成果［3-8］，绝大部分结果均表明再生粗骨料取代率是影响钢管再生混凝土结构承载能力的重要参数。为充分揭示取代率与承载性能之间的内在联系，本文通过ABAQUS 数值模拟技术对本课题组［3］前期完成的22 个圆钢管再生混凝土轴压柱试件进行有限元分析，并与试验结果进行对比;在验证数值模拟合理性基础之上，通过有限元拓展分析，分别研究再生粗骨料取代率、含钢率、长细比及截面积等因子对钢管再生混凝土轴压柱受力性能的影响，为其设计计算理论的丰富打下基础。

1 试验概述

1.1 试验设计

试验考虑再生粗骨料取代率以及钢管套箍指标两个变化参数，共设计制作了22 个试件。按圆钢管管径差异分为A、B 两个系列，每个系列再生粗骨料取代率均从0%到100%变化，并以10%为级差增长。依标准试验方法测得的钢管力学性能指标如表1 所示。对于再生混凝土的配比计算，以取代率为0%的天然混凝土配制为基准，按C30 混凝土进行强度设计。不同取代率下标准混凝土立方体试块(边长为150 mm)强度fcu，k实测值以及各试件参数见表2。试验采用位移控制的加载制度进行加载，加载装置如图1 所示。

表1 钢管力学性能指标Tab.1 Mechanical properties of steel tubes

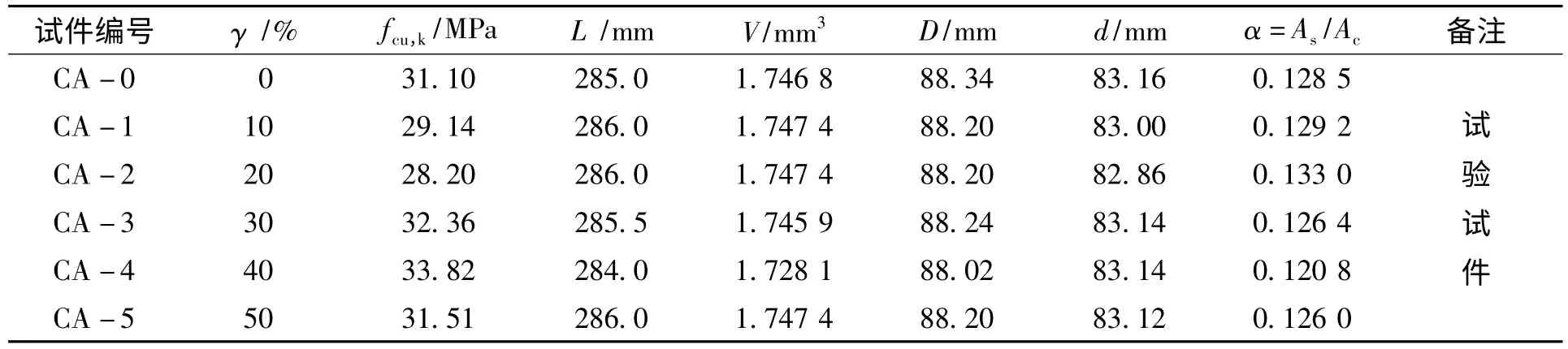
表2 试件各相关参数及实测强度Tab.2 Parameters of specimens

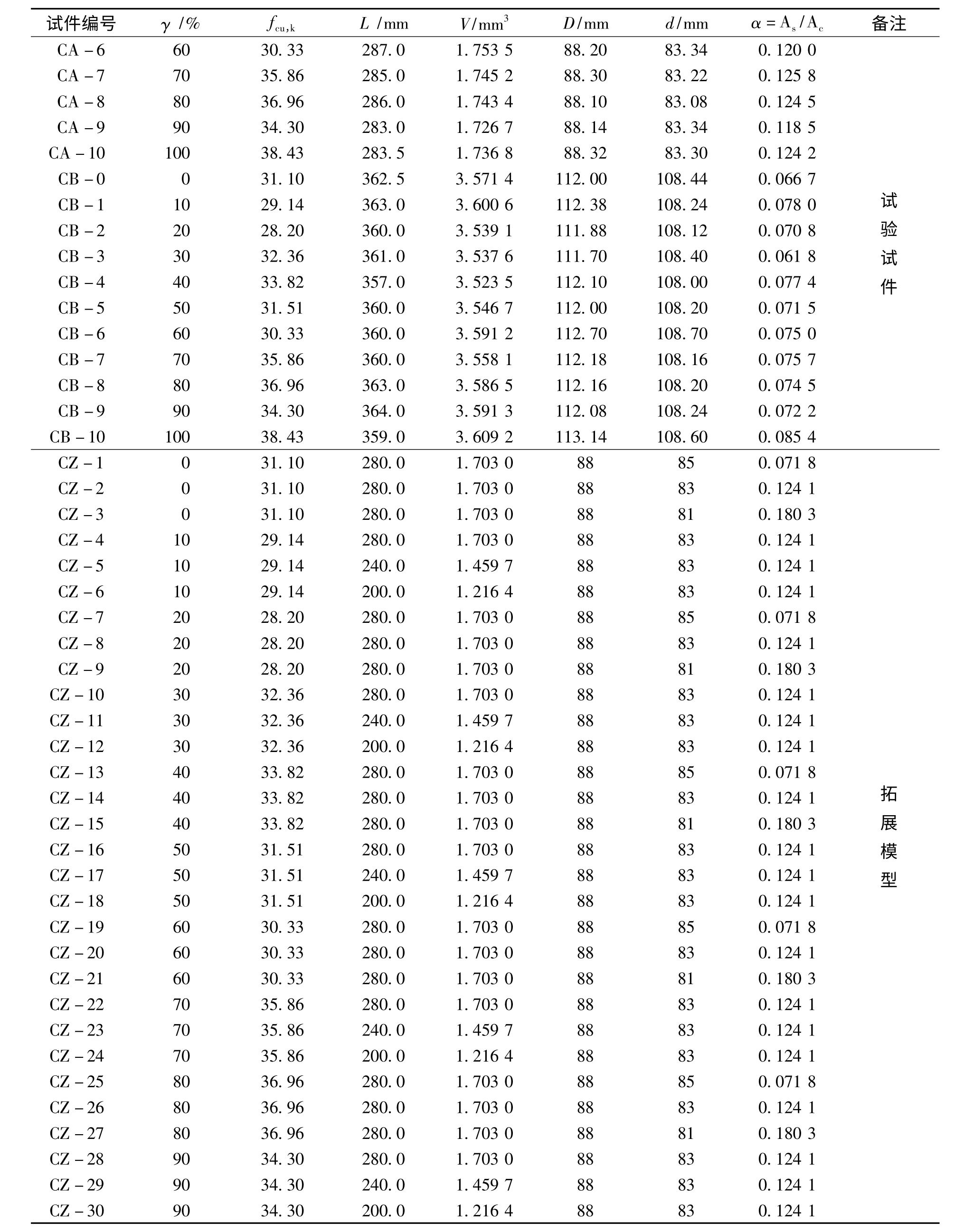
续表

图1 试验加载装置Fig.1 Loading steup

1.2 试验破坏过程及形态

试件在受力过程中，圆钢管出现了掉锈以及局部鼓曲的现象，在达到极限强度后，其承载能力有所下降，但降幅较小。在荷载变化不大的情况下，变形不断增大并伴随着钢管凸起的现象;在变形达到一定程度后，钢管外表面凸起处出现竖向裂纹。此后荷载下降，试件破坏。试件最终破坏形态呈腰鼓状斜剪压破坏，部分试件的钢管环状凸起部位还在受力后期出现撕裂现象。在加载前期和中期，钢管再生混凝土试件与普通钢管混凝土试件的破坏形态基本相同，加载后期，再生混凝土压碎程度较普通混凝土的大，最终在钢管环状凸起处撕裂破坏。

2 有限元模拟过程

2.1 模型参数

2.1.1 建模概况

利用ABAQUS 有限元分析平台，参照文献［9］提供的方法，采用分离式方法建立有限单元模型。钢管壁采用四节点完全积分格式的壳单元来模拟，在壳单元厚度方向采用九个积分点的Simpson 积分，核心混凝土采用八节点缩减积分格式的三维实体单元。采用映射网格划分的方法，模型截面的网格划分在长度方向相同。钢管与混凝土界面法线方向的接触采用硬接触，选用库伦摩擦模型来模拟钢管与核心混凝土界面切向力的传递，即界面可传递剪应力，直到剪应力达到临界值τcrit界面之间才产生相对滑动。τcrit与界面接触压力p 成比例，且不小于τbond，即τcrit=μp≥τbond，其中，对于界面摩擦系数μ，根据大量轴压算例可知取0.6 计算结果较好。钢管与核心混凝土之间的平均界面粘结力可根据已有的研究成果［10］按下式计算:τbond=2.314-0.019 5 d/t(单位:N/mm2)，其中，d 为核心混凝土的直径，t 为钢管壁厚。ABAQUS 中建立的混凝土柱模型和圆钢管模型如图2 所示。

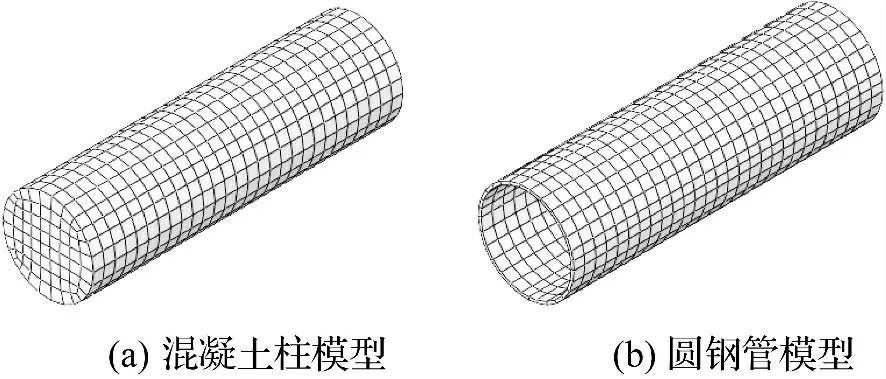
图2 混凝土柱及圆钢管模型Fig.2 Models of concrete column and circle steel tube

2.1.2 混凝土本构关系

材料本构关系的选取将影响数值模拟计算结果的精度。本文试件为钢管混凝土柱，其中核心混凝土处于三轴受压状态。ABAQUS 为低压力混凝土的非线性问题分析提供了3 种本构模型［9］，文中选取塑性损伤模型。在围压作用下，混凝土强度的提高通过定义屈服面实现，塑性性能的提高则通过核心混凝土的应力-应变关系体现。

对于混凝土受压应力-应变关系曲线，本文根据文献［11］中给出的研究成果，并考虑约束效应系数ξ 和混凝土强度fc的影响，采用其中提出的核心混凝土应力-应变关系，其表达式为:

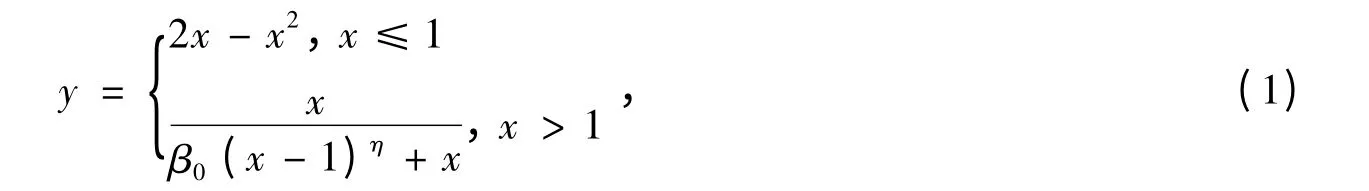
式中:x=ε/ε0，y=σ/σ0，σ0= fc，ε0=εc+800ξ0.2×10-6，η=2，εc=(1300+12.5fc)×10-6，β0=(2.36×10-5)［0.25+(ξ-0.5)7］×fc0.5×0.5，且β0≥0.12。弹性模量Ec则参考文献［12］中提出的计算方法，取混凝土弹性阶段的泊松比取为0.2。考虑再生混凝土的强度退化，参照作者所在课题组前期的研究成果［2］，再生混凝土轴心抗压强度标准值按下式确定:

对于混凝土受拉应力-应变关系，仍采用《混凝土结构设计规范》(以下简称《砼规》)［13］确定的普通混凝土单轴受拉应力-应变关系，其公式如下:

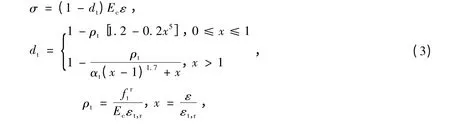
式中:αt为混凝土单轴受拉应力-应变曲线下降段的参数值，按照规范取值;dt为混凝土单轴受拉损伤演化参数;ftr为混凝土单轴抗拉强度代表值，文中取为ft;εt，r为与单轴抗拉强度代表值相应的混凝土峰值拉应变，参照文献［1］按照下列公式取值:

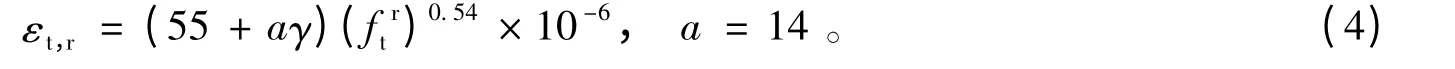
采用文献［1］的研究成果，再生混凝土的轴心抗拉强度标准值可按下式确定:

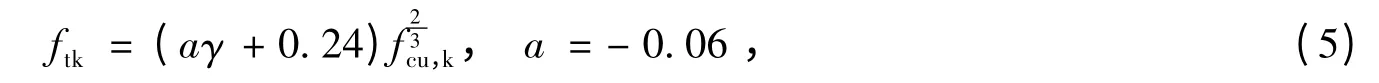
式中:γ 为混凝土再生粗骨料取代率，fcu，k为立方体试块抗压强度实测值。

2.1.3 钢材本构关系

钢材的应力强度(σi)-应变强度(εi)关系曲线一般可分为弹性段(oa)、弹塑性段(ab)、塑性段(bc)、强化段(cd)和二次塑流(de)等5 个阶段，简化后的曲线如图3 所示，其中，fp、fy和fu分别为钢材的比例极限、屈服强度和抗拉强度极限;εe=0.8 fy/Es，εe1=1.5εe，εe2=10εe1，εe3=100εe1。

2.2 模拟结果与试验结果的比较

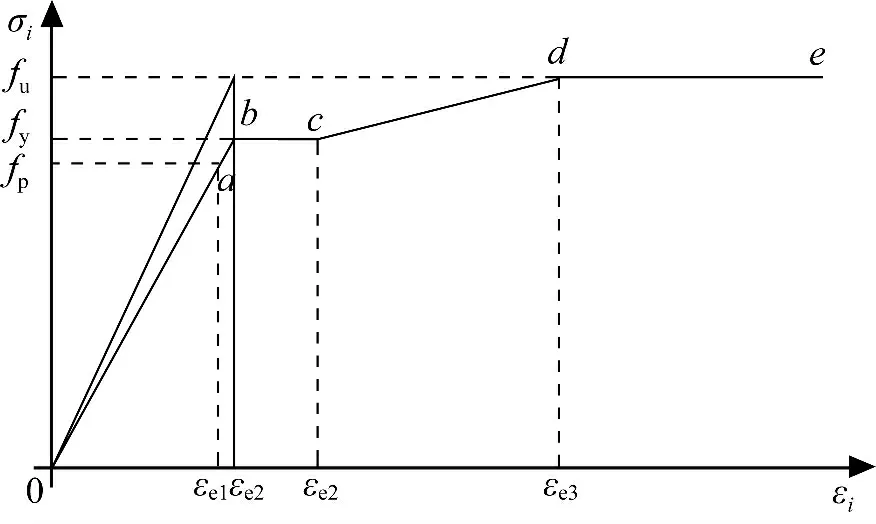
图3 钢材应力－应变关系示意图Fig.3 Streess-strain curve of steel

各试件极限荷载实测值与模拟值的对比及误差列于表3。由表3 可知，对于A 系列的试件，模拟值与计算值的比值标准差约为0.031 96，变异系数约为0.031 3;对于B 系列的试件，标准差约为0.060 5，变异系数约为0.059 2，表明各试件的模拟结果与试验值吻合较好。因此，在缺乏试验条件的情况下，可以利用ABAQUS 有限元技术实现钢管再生混凝土轴压柱的计算分析。

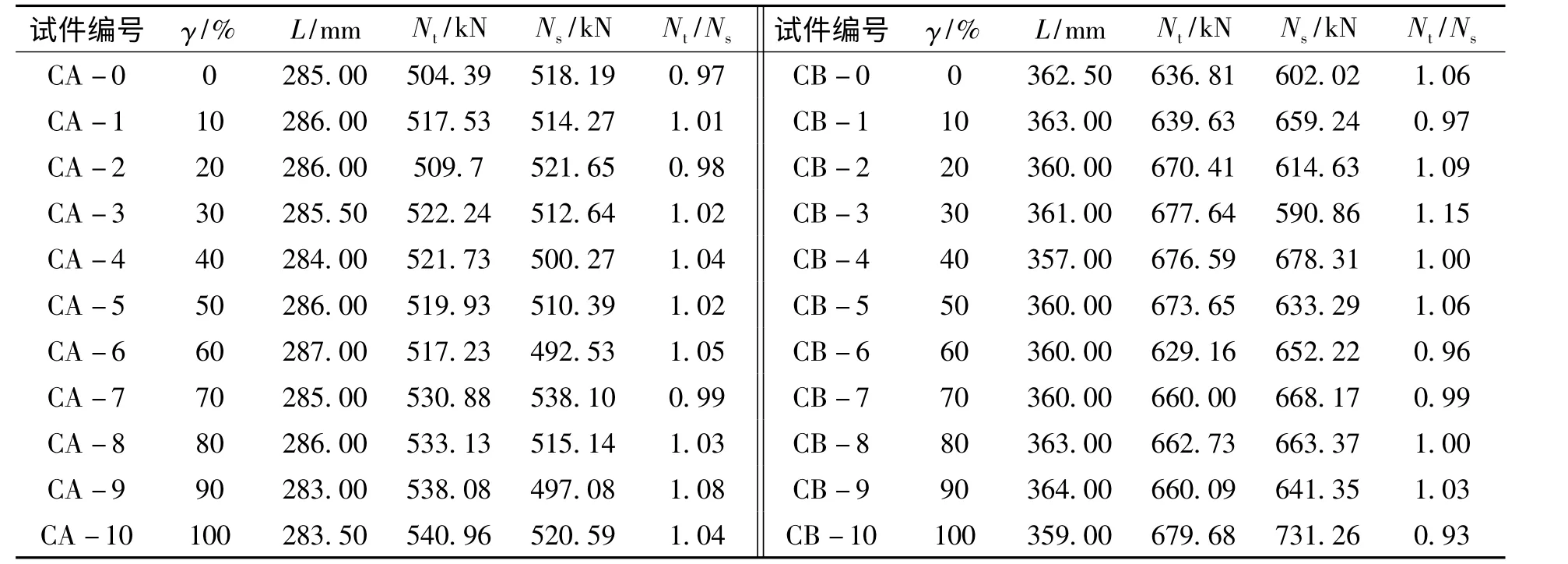
表3 极限荷载试验值与模拟值对比Tab.3 Comparison of ultimate bearing capacity between test and numerical results

3 极限承载力影响因素分析

为了深入分析圆钢管再生混凝土轴压构件的受力性能，本文在原有试验研究的基础上增设30 个圆钢管再生混凝土柱模型(模型编号CZ-1 ～CZ-30)，采用ABAQUS 数值模拟技术进行拓展分析。设计拓展模型时考虑的影响因素包括柱截面积、柱长度、钢管壁厚度等，试件相关参数见表2。本文主要研究对象为钢管再生混凝土柱在静力荷载作用下的轴压受力性能的影响因素，故未考虑钢管的局部屈曲效应对极限承载力的影响。

3.1 长细比的影响

不同长细比下的构件极限承载力变化如图4 所示。由图4 可见，随着长细比的增大，构件承载力逐渐减小，以长细比为2.27 的模型(L=200 mm，D=88 mm)为基准，经差值计算可知:①当取代率γ=10%时，长细比为2.73 的模型承载力减小5.78%，长细比为3.18 的模型承载力减小9.78%;②当取代率γ=30%时，长细比为2.73 的模型承载力减小5.88%，长细比为3.18 的模型承载力减小9.95%;③当取代率γ=50%时，长细比为2.73 的模型承载力减小5.83%，长细比为3.18 的模型承载力减小10.08%。

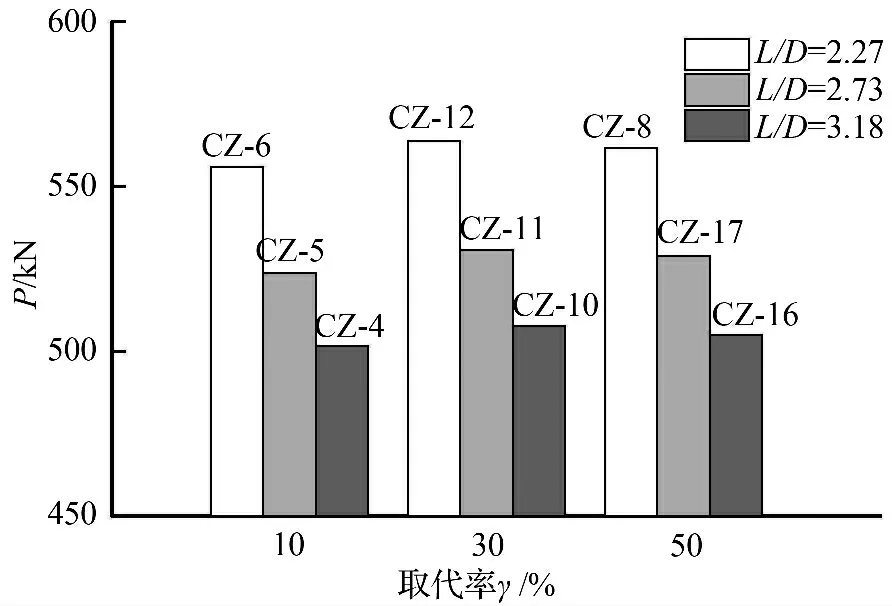
图4 长细比－极限承载力关系Fig.4 Ultimate bearing capacity under different slenderness ratios

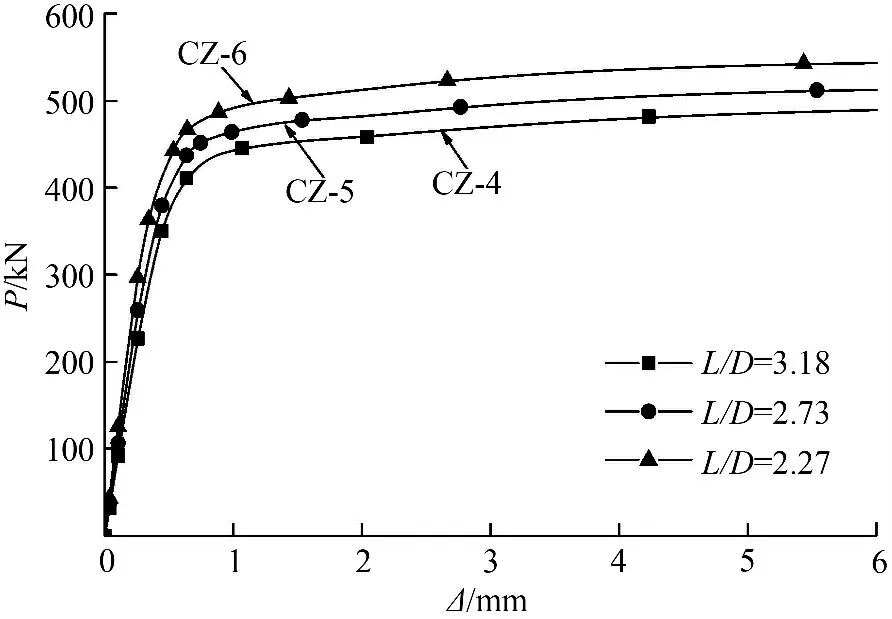
图5 不同长细比时的P－Δ 曲线Fig.5 P－Δ curves under different slenderness ratios

不同长细比下模型的轴压荷载—竖向位移曲线如图5 所示。由图5 可见，在曲线上升段，随着长细比的增大，曲线斜率逐渐减小，峰值点荷载也明显减小，峰值点对应的竖向位移变化不明显;过峰值点后，曲线随着长细比的增大未发生显著变化。可见，长细比的增加对极限荷载有不利影响，但对其非线性性质的发展影响不太显著。

3.2 含钢率(钢管壁厚)的影响

不同含钢率下的构件极限承载力变化情况如图6 所示。由图6 可见，随着含钢率的增大，构件的承载力显著增大，以含钢率α=0.071 8 的模型(L=280 mm，t=1.5 mm)为基准，经差值计算可知:①当取代率γ=0%时，含钢率为α=0.124 1 的模型承载力增长31.14%，含钢率为α=0.180 3 的模型承载力增长66.20%;②当取代率γ=20%时，含钢率为α=0.124 1 的模型承载力增长37.90%，含钢率为α=0.180 3 的模型承载力增长75.02%;③当取代率γ=40%时，含钢率为α=0.124 1 的模型承载力增长39.04%，含钢率为α=0.180 3 的模型承载力增长75.68%;④当取代率γ=60%时，含钢率为α=0.124 1的模型承载力增长35.81%，含钢率为α=0.180 3 的模型承载力增长72.32%;⑤当取代率γ=80%时，含钢率为α=0.124 1 的模型承载力增长27.72%，含钢率为α=0.180 3 的模型承载力增长60.75%。

图7 给出了当取代率γ=20%时，不同含钢率下的模型轴压荷载—竖向位移曲线分布概况。由图可见，在曲线上升段，随着含钢率的提高，曲线斜率逐渐增大，峰值点荷载也显著增大，但峰值点对应的竖向位移有减小的趋势;过峰值点后，曲线随着含钢率的提高有变陡的趋势。由此可见，含钢率的增长对构件极限荷载能起有利影响，并能提高构件的延性和耗能能力。

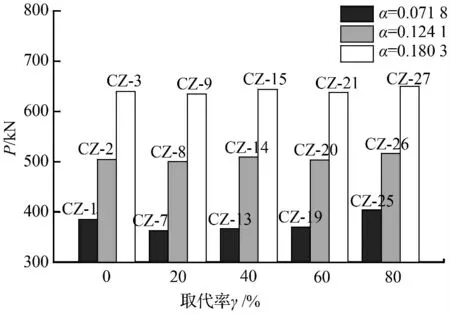
图6 含钢率－极限承载力关系Fig.6 Ultimate bearing capacity under different steel ratios

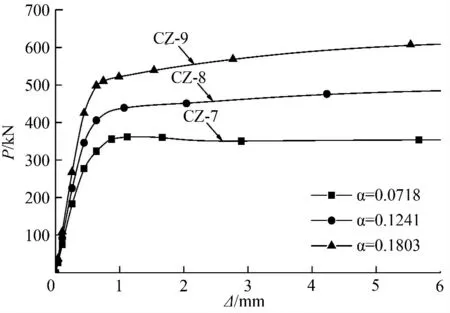
图7 不同含钢率时的P－Δ 曲线Fig.7 P－Δ curves under different steel ratios

3.3 截面积的影响

不同截面积下的构件极限承载力变化如图8 所示。由图8 可见，随着截面积的增大，构件承载力有小幅提高，以截面积为5 815.56 mm2的模型(L=280 mm，α=0.124 1)为基准，经差值计算可知:①当取代率γ=70%时，截面积为6 082.12 mm2的模型承载力增长5.01%，截面积为6 363.14 mm2的模型承载力增长9.71%;②当取代率γ=90%时，截面积为6 082.12 mm2的模型承载力增长4.91%，截面积为6 363.14 mm2的模型承载力增长9.71%。

图9 给出了当取代率γ=70%时，不同截面积下的模型轴压荷载—竖向位移曲线分布概况。由图9可见，在曲线上升段，随着截面积的提高，曲线斜率逐渐增大，峰值点荷载也逐渐提高，但峰值点对应的竖向位移有减小之势;过峰值点后，曲线随着截面积的提高而未发生显著变化。可见，截面积的增大对极限承载力的提高能起有利影响，但总体来看，对受力过程的影响不甚明显。

图8 截面积－极限承载力关系Fig.8 Ultimate bearing capacity under different sectional areas

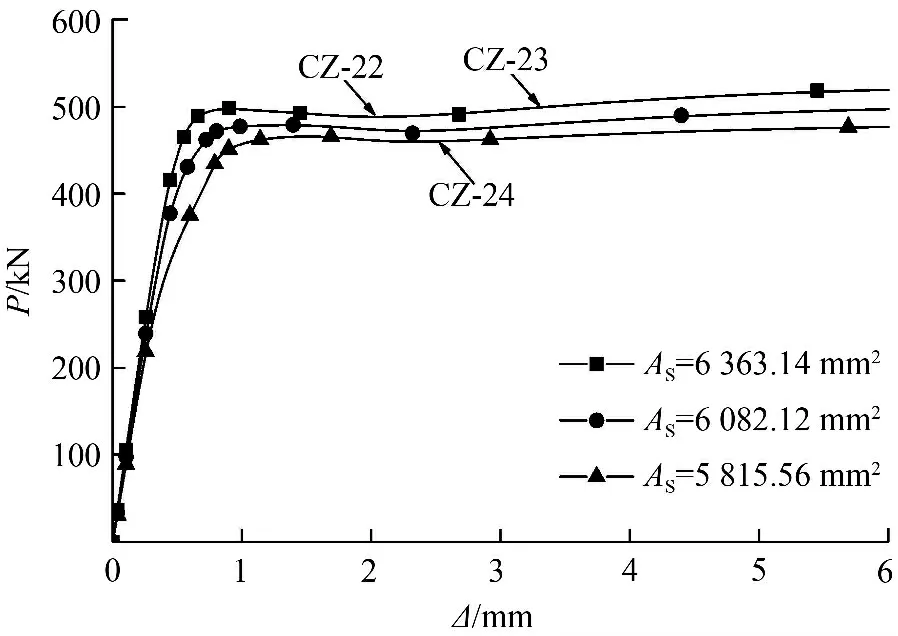
图9 不同截面积时的P－Δ 曲线Fig.9 P－Δ curves under different sectional areas

4 承载力计算方法探讨

由作者所在课题组［3］前期研究成果可知，随着再生粗骨料取代率的改变，圆钢管再生混凝土柱的承载能力也发生相应变化，因此，极有必要探讨考虑再生粗骨料取代率影响的构件承载力计算方法。本文以《钢-混凝土组合结构设计规程》(DL/T 5085—1999，以下简称《规程》)［14］为依据，考虑再生粗骨料取代率对圆钢管再生混凝土轴压柱承载力的影响，对《规程》公式予以修正，其中规定单肢钢管混凝土轴心受力构件的承载力计算公式为:

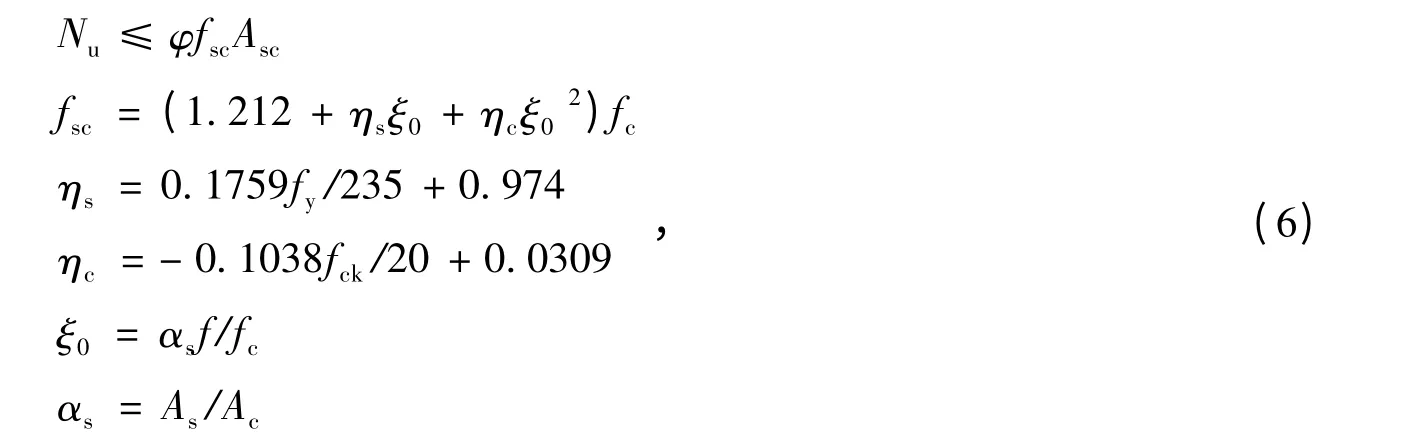
式中:φ 为与钢管长细比有关的轴心受压稳定系数，参照《规程》取值;Asc为钢管混凝土的截面面积;fsc为钢管混凝土的组合轴压强度设计值;fck和fc分别为混凝土轴心抗压强度标准值和设计值;f 为钢材的抗拉、抗压和抗弯强度设计值;fy为钢材的屈服强度;αs为截面含钢率;ξ0为截面套箍系数设计值;As和Ac分别为钢管和混凝土的截面积;ηs和ηc为计算系数。

将数值计算所得极限承载力Ns与参照规程计算所得极限承载力Nu进行比较，并引入参数μ=Nu/Ns，其计算结果如表4 所示。

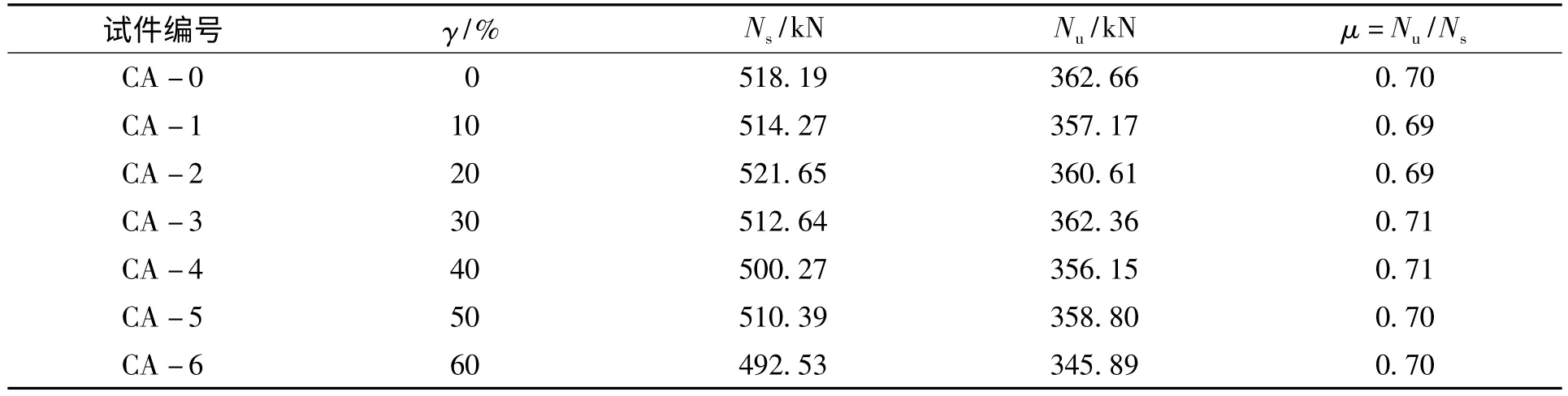
表4 μ 值计算表Tab.4 Calculation ofμ value

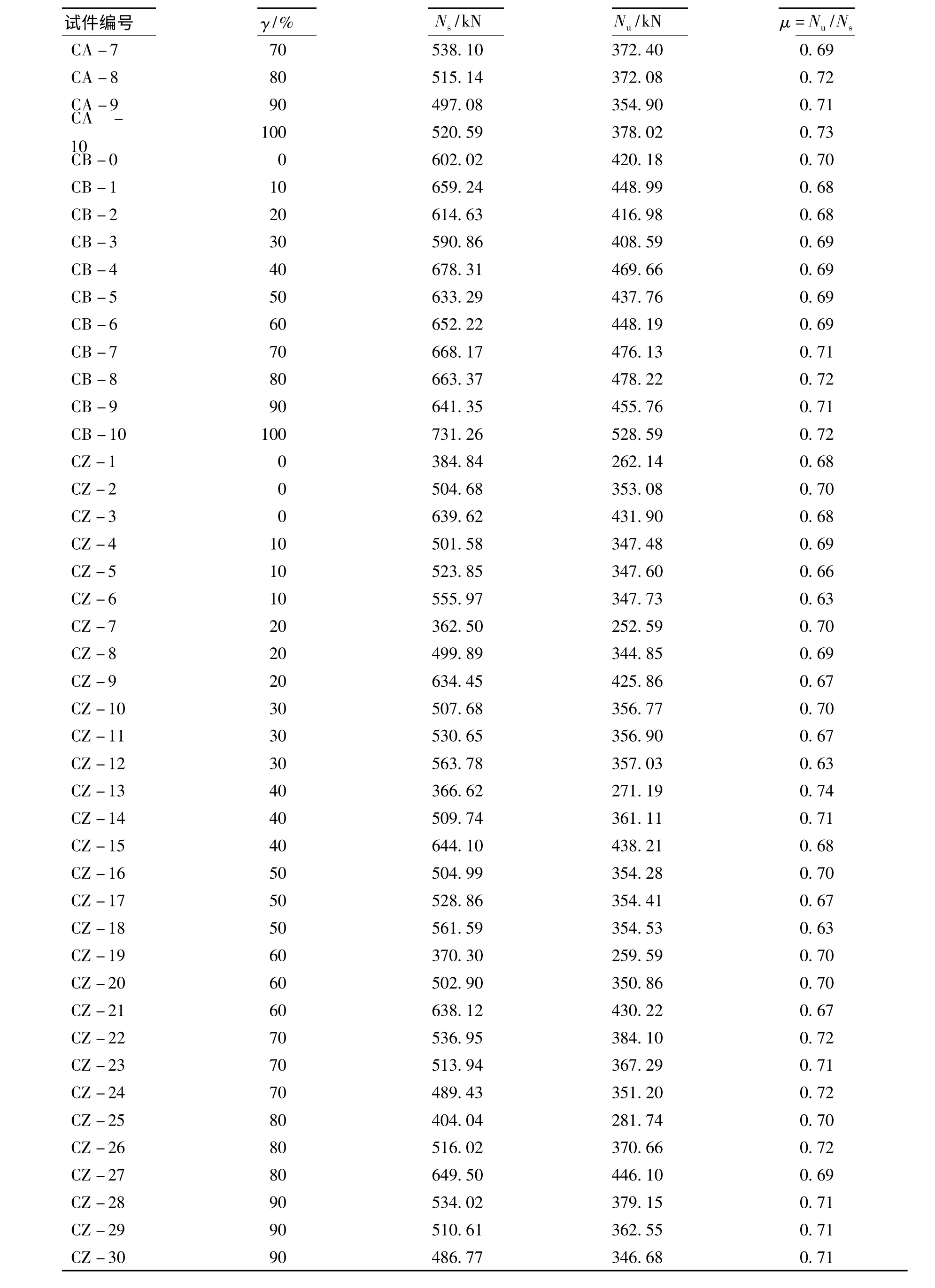
续表4

由表4 可知，模拟值比按现行规程计算结果的大，因此，规程偏于安全;然而比较可见，这种强度富余随着取代率的增加有增长的趋势。为研究μ 值与再生粗骨料取代率γ 之间的关系，本文利用MATLAB 软件对两者的数值分布进行拟合，所得拟合结果如图10 所示，其函数表达为:

由比较所得，拟合结果与原数据的误差平方和为0.020 21，标准差为0.020 1，可见拟合效果较好。

由表4 可知，μ 值最小值为0.63，最大值为0.74。考虑结构设计时的安全性，本文建议在进行圆钢管再生混凝土轴压承载力设计时，其承载力可按规程计算所得结果除以μ'=0.75 ～0.80 的安全系数，即:

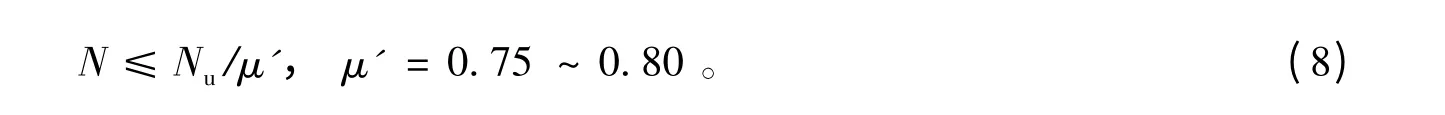
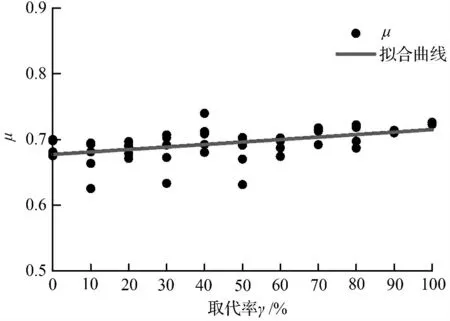
图10 μ 值曲线拟合图Fig.10 Fitting of μ value curve

5 结 论

基于试验实测得到22 个圆钢管再生混凝土柱轴压性能数据，并采用ABAQUS 软件拓展分析其在再生粗骨料取代率、含钢率、长细比及截面积等变化参数影响下的受力性能，得到如下结论:

①圆钢管再生混凝土轴压柱数值模拟的极限荷载与试验实测结果吻合较好，表明采用数值模拟技术可实现其在静力荷载作用下的受力性能分析。

②长细比的增加对极限荷载有不利影响，但对其非线性性质的发展影响不太显著;而含钢率的增长将显著提高其延性和耗能能力;在其他参数相同的前提下，增大截面积将有利于承载力的提高，但提高幅度不显著。

③采用现行《钢-混凝土组合结构设计规程》计算所得极限荷载值较试验值和模拟值的小，表明《规程》计算结果偏于保守。

④基于数值计算成果，将再生粗骨料取代率引入规程公式并予以修正，所得计算模型可为钢管再生混凝土轴压构件的设计计算提供借鉴和参考。

［1］ 肖建庄.再生混凝土［M］.北京:中国建筑工业出版社，2008.

［2］ 陈宗平，徐金俊，郑华海，等.再生混凝土基本力学性能试验及应力应变本构关系［J］.建筑材料学报，2013，16(1):24-32.

［3］ 陈宗平，张士前，王妮，等.钢管再生混凝土轴压短柱受力性能的试验与理论分析［J］.工程力学，2013，30(4)，107-114.

［4］ 张向冈，陈宗平，薛建阳，等.钢管再生混凝土轴压长柱试验研究及力学性能分析［J］.建筑结构学报，2012，33(9)，12-20.

［5］ 陈宗平，徐金俊，薛建阳，等.钢管再生混凝土黏结滑移推出试验及黏结强度计算［J］.土木工程学报，2013，46(3)，49-58.

［6］ 陈宗平，李启良，张向冈，等.钢管再生混凝土偏压柱受力性能及承载力计算［J］.土木工程学报，2012，45(10):72-80.

［7］ KONNO K，SATO Y，MAKUTA Y，et al.Property of recycled concrete column encased by steel tube subjected to axial compression［J］.Transactions of the Japan Concrete Institute，1997，19(2):231-238.

［8］ KORMO K，SAM Y，UEDA T，et a1 Mechanical property of recycled concrete under lateral confinement［J］.Transactions of the Japan Concrete Institute，1998，20(3):287-292.

［9］ Dassault Systemes Simnlia Corp.ABAQUS Analysis User's Manual［M］.Providence，RI，USA:Dassault Systemes Simulia Corp，2011.

［10］BRETT C G，CENK T，JEROME F H，et al.A synopsis of studies of the monotonic and cyclic behavior of concrete-filled steel tube beam-columns:structural engineering report［R］.Urbana，Illinois，USA:Department of Civil and Environmental Engineering，University of Illinois at Urbana Champaign，2008:179-180.

［11］韩林海，杨有福.现代钢管混凝土结构技术［M］.2 版.北京:中国建筑工业出版社，2007.

［12］ACI Committee.Building Code Requirements for Structural Concrete(ACI 318-05)and Commentary(ACI 318R-05)［S］.Farmington Hills，Michigen:Amer Concrete Inst，2004.

［13］中国建筑科学研究院.混凝土结构设计规范GB50010-2010［S］.北京:中国建筑工业出版社，2010.

［14］华北电力设计院.DL/T 5085-1999 钢-混凝土组合结构设计规程［S］.北京:中国电力出版社，1999.