Gaussian pigeon-inspired optimization approach to orbitalspacecraft formation reconfguration

School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China

Gaussian pigeon-inspired optimization approach to orbitalspacecraft formation reconfguration

ZhangShujian,DuanHaibin*

School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China

Formation confguration;

Gaussian distribution;

Gaussian pigeon-inspired

optimization(GPIO);

Orbitalspacecraft;

Pigeon-inspired optimization (PIO)AbstractWith the rapid development of space technology,orbital spacecraft formation has received great attention from internationaland domestic academics and industry.Compared with a single monolithic,the orbitalspacecraft formation system has many advantages.This paper presents an improved pigeon-inspired optimization(PIO)algorithm for solving the optimalformation reconfguration problems of multiple orbital spacecraft.Considering that the uniform distribution random searching system in PIO has its own weakness,a modifed PIO model adopting Gaussian strategy is presented and the detailed process is also given.Comparative experiments with basic PIO and particle swarm optimization(PSO)are conducted,and the results have verifed the feasibility and effectiveness of the proposed Gaussian PIO(GPIO)in solving orbital spacecraft formation reconfguration problems. ©2015 Production and hosting by Elsevier Ltd.on behalf of CSAA&BUAA.

1.Introduction

Orbital spacecraft formation is the concept that multiple spacecraft work together to achieve a common mission.Coordinating orbital spacecraft formation has more benefts than single spacecraft,including faster build time,easier launch, cheaper replacement and the ability to view research targets from multiple angles or at multiple times.These qualities make them ideal for astronomy,meteorology,communications, earth science,environmental uses and even military uses.

This problem can be solved in terms of convex optimization and some other approaches have been proposed to obtain optimal control strategies for reconfguration on other vehicles in literature.In Ref.1,closed-loop brain storm optimization is used to work out the optimal satellite formation reconfguration problem.In Ref.2,a new formation reconfguration technology is applied in other autonomous vehicles,which has a particularly instructive inspiration for spacecraft formation. In terms of controlling the spacecraft formation,an ideal autonomous attitude coordinated controller,a robust adaptive attitude coordinated controller and a fltered robust adaptive attitude coordinated controller are proposed to deal with the issue in Ref.3.A method for fuel-optimal trajectories considering collision avoidance designing is discussed based on mix-integer linear programming in Ref.4.Inalhan et al.5studied relative dynamics and the spacecraft formation controlling system in eccentric orbits.Furthermore,in Ref.6,an analyticalfuel-optimal impulsive formation reconfguration strategy from the perspective of relative orbital elements is presented.

Swarm intelligence optimization has obtained increasing attention from researchers in the last two decades.Some optimization algorithms have been proposed and studied during these years,including particle swarm optimization(PSO),7,8ant colony optimization(ACO),9brain storm optimization (BSO)10and the artifcial bee colony(ABC)algorithm.11In Ref.12,co-evolutionary PSO is used on satellites’formation reconfguration.Although these optimization algorithms have remarkable performance in solving optimization problems, there is also large room for improvement in terms of the convergence rate and global searching abilities.The pigeoninspired optimization(PIO)algorithm is a novelswarm intelligence algorithm,which was frstly proposed by Duan and Qiao in 2014.13It can accelerate the convergence speed impressively. Thus this paper will adopt the PIO as a research target.

Although PIO solves the convergence rate problem,the ability of global searching is still not optimistic.In order to overcome this weakness in PIO,a Gaussian item is introduced to balance the importance between exploration and exploitation results.In this paper,this Gaussian PIO algorithm (GPIO)is used for optimal trajectory design in cooperative orbitalspacecraftformation reconfguration,namely,to design an optimalroute for the spacecraft when they need to reach a new formation required for different missions.For the reason that the lifetime of spacecraft is limited,one of the mostimportant constraints for the optimal trajectory is overall fuel cost minimization.The other two constraints are easy to understand,that is,collision avoidance and fnal confguration.1Specifcally,the collision avoidance is the basic requirement and has to be satisfed at any time.

2.Problem formulation

In order to apply the swarm intelligence optimization algorithms to solve the complex dynamic problems,the orbital spacecraftformation reconfguration problem has to be simplifed.This section aims at formulating the spacecraft formation reconfguration problem so that the parameters in the algorithm can be obtained easily.

2.1.Coordinate system

The length of the orbital spacecraft can be ignored compared with the distance between two spacecrafts.According to the relative motion dynamics,each spacecraft can be modeled as one mass point.The coordinate system is shown in Fig.1. The reference spacecraft is represented by L,which means the leader spacecraft,and F represents the follower spacecraft. The x coordinate is in the radial direction,y-axis is in the intrack direction,and the z component is in parallel with the angular momentum direction.

2.2.Dynamics model

In this paper,three fundamental assumptions have to be satisfed14:

(1)Assume that the Earth is a homogeneous globe and ignore any perturbation.

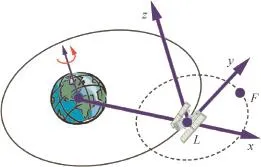
Fig.1 Coordinate system.

(2)The eccentricity of the orbitalspacecraft orbit,including the reference spacecraft and the follower ones,should be equal to zero.

(3)The distance between the reference spacecraft and the follower spacecraft is much less than the orbit radius.

To describe the relative motion between the spacecraft, Hill’s equation,which is also known as Clohessy-Wiltshire (CW)equation,3is the most widely used approximation based on the fundamental assumptions mentioned above.Generally, it can be expressed as

where x,y and z are the F coordinates in the above coordinate system;ux,uyand uzare the controlinputs in x-axis,y-axis and z-axis directions,respectively;ωis the average orbit angular velocity.

2.3.Two-impulse control mathematical model

In order to describe the complex motion of the orbital spacecraft formation with the Hill’s equation,the orbital spacecraft formation reconfguration is supposed to satisfy the three constraints.First,the orbit of the reference spacecraft has to be in the shape of a circle or an approximative circle.Second,in the two-impulse controlmathematicalmodel,the whole power for the follower spacecraft should be originated from these two impulses.In other words,during the spacecraft formation reconfguration process,only the predesigned two impulses provide the power.Third,the error of the follower spacecraft’s relative position can be ignored by comparing with the distance between the spacecraft.14Under these assumptions,the control inputs ux,uyand uzin Eq.(1)are equal to zero.Thus

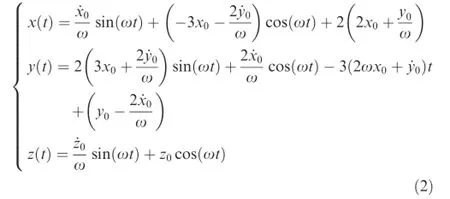
where x0，y0，z0，˙x0，˙y0and ˙z0are the initial states of the spacecraft.

According to Eq.(2),the state transition-matrixΦ(t)can be expressed as

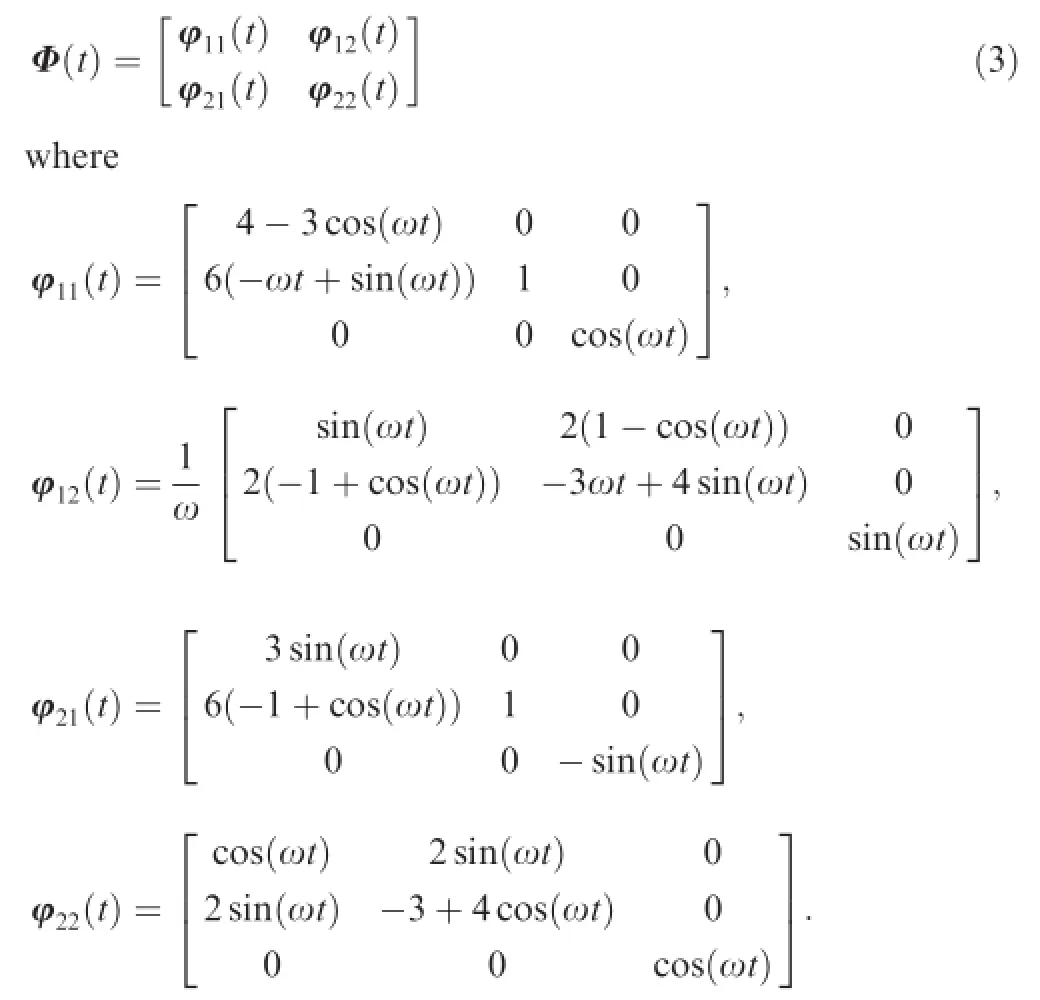
At time t,the relative position vector r(t)and the relative speed vector v(t)are[x(t),y(t),z(t)]Tand［˙x（t），˙y（t），˙z（t）］T. After a periodΔt,the relative motion state can be transformed to

In the typicalspacecraft formation reconfrmation problem, t1and t2(0＜t1＜t2＜tw)can be defned as the exacttime for activating the two impulses,with twthe whole controltime.Let the initialstate of the spacecraft be,and the fnal state can be given by

According to the above analysis and the two-impulse control precondition,we have

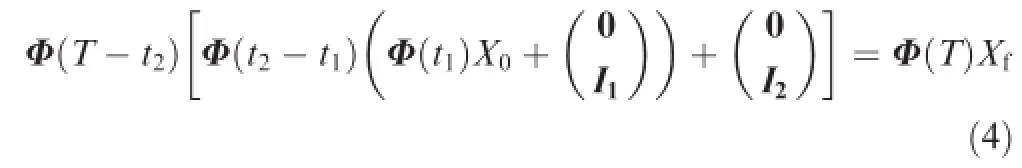
where I1and I2are the control impulses at t1and t2time respectively.

Based on the transition-matrix properties,the Eq.(4)can be expressed as

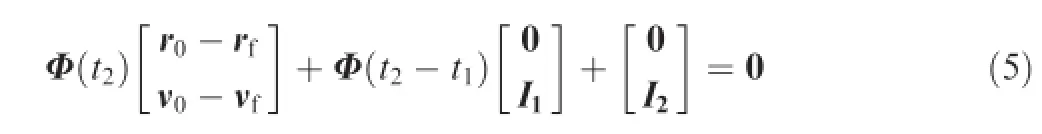
Therefore,the two control impulses and the solutions of Eq.(5)can be expressed as12

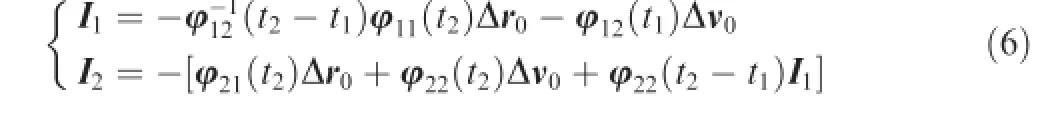
whereΔr0andΔv0are the changes of position vector and velocity vector and

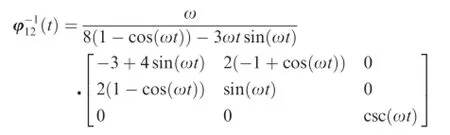
Obviously,on the premise that the beginning state,the fnal state and the whole controlling time tware settled,how much fuel the orbital spacecraft formation reconfguration costs can be determined by the timing of activate the two impulses. Therefore,the spacecraft formation reconfguration problem is transformed into a typical fnding-best-timing problem.

2.4.Collision avoidance

In order to avoid the various collisions in the space,each pair spacecraft has to keep a safety distance during the formation confguration process and collision avoidance has to be the frst requirement.Assume that all the spacecraft are sphere, and the distance between the geometry center and the farthest point on the spacecraft is the radiusThus,the minimum safety distance is R and the constraint inequality iss

where ri(t)=[xi(t),yi(t),zi(t)]Tand rj(t)=[xj(t),yj(t),zj(t)]Trepresent the position of spacecraft i and j at time t;‖·‖denotes the 2-norm of a matrix or a vector.

3.Gaussian pigeon-inspired optimization

3.1.Pigeon-inspired optimization

In recent years,population-based swarm intelligence algorithms have been studied in depth and used in many areas to solve optimization problems.Among them,PSO is a classic one,which has been applied in many felds.However,the convergence speed of basic PSO is not effective enough to solve some complex optimization problem.Generally,the basic PSO would be trapped into a locally optimal solution.Concerning this issue,the PIO makes particular improvement.In nature,pigeons can fnd their destinations by relying on the sun,magnetic feld and landmarks.The basic PIO has two operators,which are map and compass operator,and landmark operator.The map and compass operator is based on magnetic feld and sun,and the landmark operator is based on landmarks.

3.1.1.Map and compass operator

After defning N as the number of the pigeons,D as the number of dimensions,T1as the maximum iterations and initializing each pigeon’s position x and velocity v,it is necessary to settle a rule for position and velocity updating.Naturally, the map and compass can help the pigeons fnd their destinations.In PIO model,the map and compass operator assists each virtual pigeon to search the resolution space in each iteration.The rule can be expressed as13

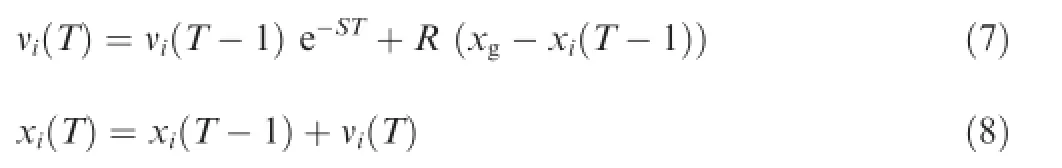
where T is the number of iterations;vi(T)is the velocity of pigeon i in T-th iteration;xi(T)is the position of pigeon i in T-th(0＜T≤T1)iteration;S is the map and compass factor; R is a random number between 0 and 1;and xgis the current global best position.

3.1.2.Landmark operator

In nature,when pigeons approach to their destinations,they use landmarks as a guide instead of map and compass. Similarly,in PIO model,there is a landmark operator so that the convergence speed can be improved.Let T2be the maximum iterations,xcthe center of a group of pigeons and f(x) the ftness value calculating function.According to f(x),sort the xiand fnd the center as xc.In each iteration,after fnding out the center of the pigeons,the number of the pigeons is going to be cut to a half.Those,who are far away from the destination,are supposed to follow near the destination ones. Thus,the updating rule is given by13

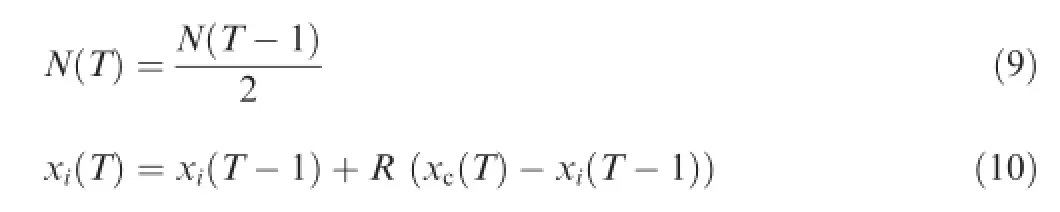
3.2.Gaussian pigeon-inspired optimization

PIO has a fast convergence speed,but stillhas a certain possibility trapping into a locally optimalsolution.PIO also has the common problem,which is how to balance the importance between exploration and exploitation.To formulate a more effcient model,a Gaussian item is added to the position iteration.

3.2.1.Gaussian distribution

The random number R has an obvious feature that the random output R is a uniform distribution.It has a signifcant advantage which is the ability offull-scale searching.Gaussian distribution,also known as normal distribution,is extensively used in natural and social sciences.It has two parameters,which areμandσ.The parameterμin this defnition is the mean or expectation of the distribution(also its median and mode). The parameterσis its standard deviation,and its variance isσ2.

In many cases,the optimization algorithm should have the ability of concentrated searching when it can be sure that the destination is right there.The method to get a random number,which satisfy the uniform distribution rule,is not good enough to meet the requirements.The searching equation in the PIO landmark operator satisfes the latent premise of Gaussian distribution and it can be improved for achieving the global best.

3.2.2.Gaussian item

The improved position updating equation in PIO landmark operator is given as

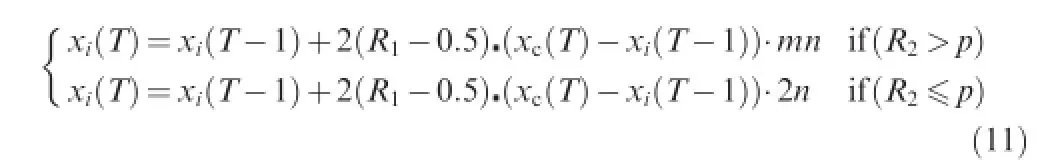
where p is a fexible parameter in order to balance the normal distribution and the uniform distribution;R1and R2are two random numbers from 0 to 1.

where Rnis a random number created according to the Gaussian distribution between 0 and 1;T2is the maximum iteration.15

4.The proposed GPIO for orbital spacecraft formation reconfguration

4.1.Process of basic PIO

Step1.Initialize the parameters,including the initial position and velocity of each pigeon.

Step2.Calculate each pigeon’s ftness value.

Step3.Search the best current position for each pigeon by comparing each pigeon’s ftness value.

Step4.Search the best global position by comparing each pigeon’s current best position.

Step5.Update the position and velocity based on Eqs.(7) and(8),which is achieved by map and compass operator.

Step6.If T＞T1,start the landmark operator,otherwise go to Step 5.

Step7.According to Eq.(10),update the pigeon’s position by using landmark operator.

Step8.If T＜T2,output the result,else return to Step 7.

4.2.GPIO for formation reconfguration

The process of GPIO is similar to the basic PIO process except the landmark operator.After adopting the landmark operator, three new parameters,m,n and p,should be assigned with initial values.The pigeon’s position can be updated by using Eq.(11).In addition,according to the Eqs.(12),m and n have the fxed calculating methods,but p is fexible.p is a weight factor which is responsible for the balance between uniform and Gaussian distribution.In other words,m and n are invariables regardless of situations,but p varies according to the situations.In this paper,p is equal to 0.3.

4.3.Algorithm fow of GPIO

Step1.Initialize the parameters,including the orbit parameters and the algorithm initialization parameters.

Step2.Calculate each pigeon’s ftness value.

Step3.Imitate the steps of PIO.Search the best current position and the best global position.Then update the positions and velocities by using the map and compass operator.

Step4.If T＞T1,go to step 5,otherwise,go back to Step 3.

Step5.Operate the landmark operator.

Step6.Set two parameters,m and n according to the Eq.(12).Set the balance factor p.

Step7.According to Eq.(11),update the pigeon’s position.

Step8.If T＜T2,output the result,else return to Step 7.

5.Experimental results

In order to verify the feasibility and effectiveness of our proposed GPIOfor solving orbitalspacecraft formation reconfguration problem,a series of comparative experiments are conducted by using PSO,PIO and the proposed GPIO,withconstraints of overall fuel minimization,fnal confguration and collision avoidance.The whole running time of the three algorithms are recorded for measuring the effciencies of each algorithm.To simplify the problem,the comparative experiments are designed to be geometrically perfect,and the initial and fnal confgurations are on circular orbits.The orbit parameters of the three spacecraft are given in Table 1.1Based on the initialorbit parameters,the 3 dimensional(3D)diagram is shown in Fig.2.

Table1 Orbit parameters of three orbital spacecraft.

In Fig.2,the three orbitalspacecraft initially move on a circular orbit(marked with black)forming an equilateraltriangle in space.On the larger orbit(marked with green),the three orbitalspacecraft compose another equilateraltriangle as their fnal confrmation.

For PSO,set the number of particles Num=50,the maximum iteration G=100,two evolution parameters C1=C2=1.5.For PIO and GPIO,T1=90,T2=30, Num=30,S=0.1,μ=0,δ=1.The results of these three comparative algorithms are shown in Fig.3.

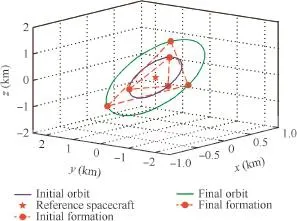
Fig.2 Formation reconfguration for three orbital spacecraft.

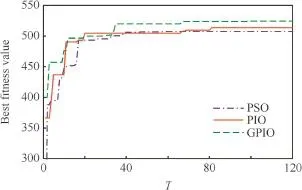
Fig.3 Convergence curves of PSO,PIO and GPIO.

Optimal impulses for each orbital spacecraft and comparison of the three algorithms’running time are shown in Tables 2 and 3.From that,it is obvious that the best results are from the GPIO and the control timing obtained by GPIO.

The above situation is that the three orbital spacecraft can transform from a smaller formation to a bigger one.Now,consider an opposite situation,which is from the bigger orbit to the smaller orbit and the orbit parameters are the same.The comparative convergence curves are given in Fig.4,and the whole running time is in Table 4.The results show that our proposed GPIO is more effcient in solving the orbital spacecraft formation reconfguration problems.

Table2 Optimal impulses for each orbital spacecraft.

Table3 Comparison of running time.

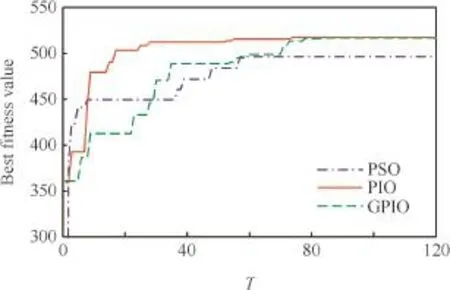
Fig.4 Convergence curves of PSO,PIO and GPIO.

Table4 Comparison of running time.

6.Conclusions

(1)PSO,PIO and GPIO are all feasible optimization algorithms in solving the orbitalspacecraft formation reconfguration problems.The convergence rates of PIO and especially GPIO are much better than basic PSO.

(2)The comparative results have shown that the performance of our proposed GPIO performs best for solving orbitalspacecraft formation reconfguration problems in various conditions.

(3)The robustness of GPIOis satisfed butnot perfect.How to improve the robustness of GPIO is one focus of our future work.

Acknowledgements

This work was partially supported by the National Natural Science Foundation of China(Nos.61425008,61333004, 61273054),the Top-Notch Young Talents Program of China, and the Aeronautical Science Foundation of China(No. 20135851042).

1.Sun CH,Duan HB,Shi YH.Optimal satellite formation reconfguration based on closed-loop brain storm optimization.IEEE Comput Intell Mag 2013;8(4):39–51.

2.Zelinski S,Koo TJ,Sastry S.Optimization-based formation reconfguration planning for autonomous vehicles.Proceedings of IEEE international conference on robotics and automation;2003, Sept 14–19;Taipei.Piscataway,NJ:IEEE;2003.p.3758–63.

3.Zheng Z,Song SM.Autonomous attitude coordinated controlfor spacecraft formation with input constraint,model uncertainties, and disturbances.Chin J Aeronaut 2013;26(2):343–9.

4.Richards A,Schouwenaars T,How JP,Feron E.Spacecraft trajectory planning with avoidance constraints using mixed-integer linear programming.J Guid Control Dyn 2002;25(4):755–64.

5.Inalhan G,Tillerson M,How JP.Relative dynamics and control of spacecraft formations in eccentric orbits.J Guid Control Dyn 2002;25(1):48–59.

6.Wang JH,Zhang JX,Cao XB,Wang F.Optimal satellite formation reconfguration strategy based on relative orbital elements.Acta Astronaut 2012;76:99–114.

7.Kennedy J,Eberhart R.Particle swarm optimization.Proceedings of IEEE international conference on neural networks;1995;Perth, Australia.Piscataway,NJ:IEEE;1995.p.1942–8.

8.Jatmiko W,Sekiyama K,Fukuda T.A PSO-based mobile robot for odor source localization in dynamic advection-diffusion with obstacles environment:theory,simulation and measurement. IEEE Comput Intell Mag 2007;2(2):37–51.

9.Dorigo M,Maniezzo V,Colorni A.Ant system:optimization by a colony of cooperating agents.IEEE Trans Syst Man Cybern Part B 1996;26(1):29–41.

10.Shi Y.Advances in swarm intelligence.Berlin:Springer;2011,p. 303–9.

11.Karaboga D.An idea based on honey bee swarm for numerical optimization[dissertation].Kayseri:Erciyes University;2005.

12.Huang HB,Ma GF,Zhuang YF,Lyu YY.Satellite formation reconfguration using co-evolutionary particle swarm optimization and Pareto optimal solution.Acta Aeronaut Astronaut Sin 2011; 32(11):2073–82.

13.Duan HB,Qiao PX.Pigeon-inspired optimization:a new swarm intelligence optimizer for air robot path planning.Int J Intell Comput Cybern 2014;7(1):24–37.

14.Zhang YK.Study on dynamics and controltechnology of satellite formation fying[dissertation].Changsha:National University of Defense Technology;2002[Chinese].

15.Dos Santos Coelho L,Alotto P.Gaussian artifcial bee colony algorithm approach applied to Loney’s solenoid benchmark problem.IEEE Trans Magn 2011;47(5):1326–9.

ZhangShujianis currently a student in the School of Automation Science and Electrical Engineering,Beihang University.His current research interests include bio-inspired computation and autonomous fight control.

DuanHaibinis currently a professor and PhDsupervisor in the School of Automation Science and Electrical Engineering,Beihang University.He is the head of Bio-inspired Autonomous Flight Systems (BAFS)Research Group of Beihang University.His current research interests include bio-inspired computation,autonomous fight control and bio-inspired computer vision.His academic homepage is:http:// hbduan.buaa.edu.cn

Received 23 July 2014;revised 22 August 2014;accepted 30 October 2014 Available online 26 December 2014

*Corresponding author.Tel.:+86 10 82317318.

E-mail address:hbduan@buaa.edu.cn(H.Duan).

Peer review under responsibility of Editorial Committee of CJA.