Consensus based on learning game theory with a UAV rendezvous application

UniversityofTorontoInstituteforAerospaceStudies,4925DufferinStreet,Toronto,OntarioM3H5T6,Canada

Consensus based on learning game theory with a UAV rendezvous application

LinZhongjie,LiuHughhong-tao*

UniversityofTorontoInstituteforAerospaceStudies,4925DufferinStreet,Toronto,OntarioM3H5T6,Canada

Consensus;

Distributed algorithms;

Fictitious play;

Game theory;

Multi-agent systems;

Potential gameAbstractMulti-agent cooperation problems are becoming more and more attractive in both civilian and military applications.In multi-agent cooperation problems,different network topologies will decide different manners of cooperation between agents.A centralized system will directly controlthe operation of each agent with information fow from a single centre,while in a distributed system,agents operate separately under certain communication protocols.In this paper,a systematic distributed optimization approach will be established based on a learning game algorithm. The convergence of the algorithm will be proven under the game theory framework.Two typical consensus problems will be analyzed with the proposed algorithm.The contributions of this work are threefold.First,the designed algorithm inherits the properties in learning game theory for problem simplifcation and proof of convergence.Second,the behaviour of learning endows the algorithm with robustness and autonomy.Third,with the proposed algorithm,the consensus problems will be analyzed from a novel perspective. ©2015 Production and hosting by Elsevier Ltd.on behalf of CSAA&BUAA.

1.Introduction

Multi-agent cooperation problems are becoming more and more attractive in both civilian and military applications,such as the real-time monitoring of crops status,monitoring the traffc situation,1,2forest fre monitoring,3,4surveillance5–7and battle feld assessment.8In multi-agent cooperationproblems,different network topologies will infuence different manners of cooperation between agents.A centralized system willdirectly controlthe operation of each agent with information fow from a single centre,while in a distributed system, agents operate separately under certain communication protocols.

There are many related studies on distributed multi-agent cooperation problems such as focks,9swarms,10,11sensor fusion12,13and so on.The theoreticalframework for constructing and solving consensus problems within networked systems was introduced in Refs.14–17.

For distributed multi-agent systems,there are three challenges need to be addressed to achieve cooperation among a potentially large number of involving agents:

(1)Limited information for agents to utilize to achieve the global objective.

(2)The information of the distributed network topology is unknown to agents.

(3)The network can be dynamic,such as stochastic networks or switching networks.

To construct a game theory model for a distributed multiagent cooperation problem:frst,the agents of the game and their strategy domains needs to be identifed,in which agents are considered as myopic and rational players;second,based on the strategy domains and the mission requirement,a global cost function that refects the performance of the joint actions will be constructed;third,an optimal strategy will be derived out based on the established global cost function.Therefore, in order to achieve cooperation in a distributed network among myopic agents,the designed game will yield the lowest costs for allagents if and only if when their strategies willbeneft the global objective.

Based on bargaining game concept,the author suggests a useful strategy for task assignment and resource distribution problems with a smallnumber of agents.18An approach is proposed for consensus problems based on cooperative game theory and bargain game theory.19A distributed optimization algorithm is designed based on the state potential game framework.20,21

In classical game theory,agents are assumed to be able to correctly anticipate what their opponents will do.It may be unrealistic in practice.In real application,agents cannot introspectively anticipate how others will act in distributed networks,especially in games with a large number of participants.Unlike classical game theory,learning game theory does not impose assumptions on agents’rationality and believes,but assumes instead that agents can learn over time about the game and the behaviour patterns of their opponents.

The preliminary result was presented.22In this paper,a systematic distributed optimization approach will be established based on a learning game algorithm.The convergence of the algorithm will be proven under game theory framework. Two typicalconsensus problems willbe analyzed with the proposed algorithm.

2.Preliminaries

For a game G（N，（Ui，i∊N），（Ji，i∊N））,Uirepresents agent i’s strategy domain with its element asμi.The collected strategy domain of Uiis denoted as U=×i∊NUiwith its element as μ=（μi，μ-i）,whereμ-idenotes the strategies of other agents besides agent i.The cost function for agent i is denoted as Ji（μi，μ-i）,which implies that agent i’s cost depends both on its own strategy and on every other agent’s strategy.

2.1.Governing equation

Fictitious play algorithm is adopted for designing the distributed optimization algorithm in this work.It is a variant of a‘stationary Bayesian learning’process.In fctitious play, agents assume behaviour patterns of their competitors were stationary.22

Consider a 2×2 matrix game

where aij（i=1，2;j=1，2）represents the cost of Agent 1 according to its strategies｛μ11，μ21｝and bij（i=1，2;j=1，2）is the costof Agent2 for its strategies｛μ12，μ22｝.Agents willdecide their strategies based on their current empirical frequency for their opponents.The algorithm starts with an initial empirical frequency

Take Agent 1 as an example,according the empirical frequency of Agent 1,the cost for each strategy is

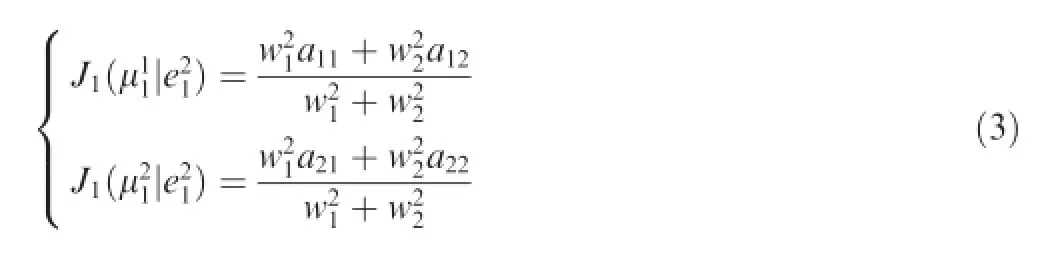
Both agents willchoose the strategies that yields the lowest cost based on their own empirical frequencies.At the end of each game,agents will update their empirical frequency according to their opponents’strategies in the previous game.

Defnition1.(ε-dominate23).A strategyμi∊Uiisε-dominated by another strategy^μi∊Ui,if for anyμ-i∊U-i,there exists Ji（μi，μ-i）＞Ji（^μi，μ-i）+ε.The set ofε-dominate strategy domain of agent i is denoted as

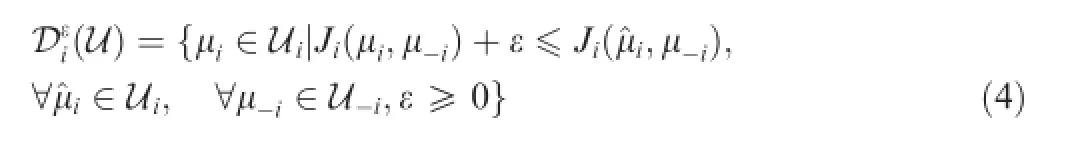
According to the defnition of theε-dominate domain,an adaptive learning is defned as

Defnition2.(Adaptive learning23).A sequence of strategy for agent i as｛μi（t）｝is consistent with adaptive learning,if

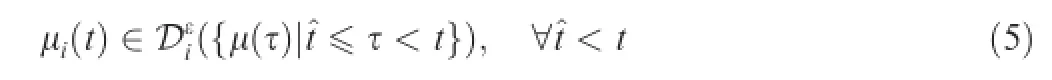
Defnition3.(Nash equilibrium).A strategyis called a Nash Equilibrium of game G（N，｛Ui，i∊N｝，｛Ji，i∊N｝）,if and only if

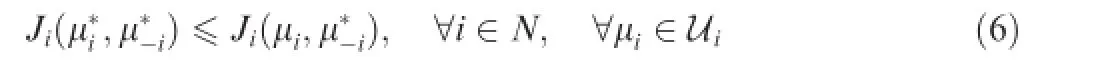
Defnition4.(Convergence).The sequence｛ζ（t）｝converges to ζif and only if there is a T＞0 such thatζ（t）=ζfor all t≥T.

Lemma1.(Adaptive learning convergence23).If certain strategy sequence｛μi（t）｝is consistent with adaptive learning and it converges to,thenbelongs to a pure strategy Nash equilibrium

2.2.Potential games

The potentialgame concept is important for distributed multiagent cooperation problems.

Defnition5.(Potential game24).A game G（N，｛Ui，i∊N｝，｛Ji，i∊N｝）is a potentialgame if there exists a global function Φ（μi，μ-i）such that

If the strategy domain for every agent of a potentialgame is bounded,this game is defned as a bounded potential game.

The potential game concept provides a valuable theoretical framework for distributed multi-agent cooperation problems. First,a game admits the potential property is guaranteed to possess a Nash equilibrium.Second,from the defnition of a potentialgame,the Nash equilibrium for every localcost function is consistent with the globalobjective.The potentialgame framework,therefore,provides distributed optimization problems with theoretical support for problem simplifcation. Many design methodologies25–27can be adopted to derive a potential game according to the global objective.

2.3.Continuous and discrete consensus algorithm

The interaction topology of a network can be denoted as G（N，ε）with the set of agents N and edgesε.The set of the neighbours of agent i is denoted as Ni=｛j∊N|（i，j）∊ε｝. An adjacent matrix A=［aij］∊Rn×nis defned as

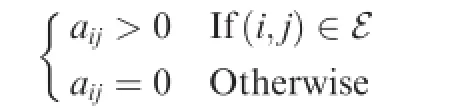
The Laplacian matrix L=［lij］∊Rn×nis defned as that∑and lij=-aijif i≠j.

Defnition6.(Stochastic matrix).A nonnegative square matrix is a row stochastic matrix if its every row is summed up to one.28,29

The product of two stochastic matrices is still a stochastic matrix.A row stochastic matrix P∊Rn×nis a stochastic indecomposable and aperiodic(SIA)matrix,if limk→∞Pk=1yTwith y∊Rn×n.

The continuous-time consensus algorithm for single integrator system is described as

Its Laplacian matrix form is represented as

The consensus algorithm in Eqs.(8)and(9)is for a singleintegrator system with dynamics as˙xi=ui.From Eq.(9),the discrete consensus control law is derived as

The matrix A(k)is row stochastic matrix,which suggests that

and

3.Distributed optimization algorithm

Under a centralized network,the centre can obtain information from all agents and conduct the optimization.For a distributed system,only partial information is available for each agent due to the distributed network topology.

According to the mission requirement of a distributed multi-agent cooperation problem,the global cost function is defned as

and the optimization purpose ofthis problem is to fnd optimalthat satisfes

In a distributed system,the only information available for agent i is its own local state xiand the information from its neighbours｛xj，j∊Ni｝.A distributed optimization algorithm,therefore,aims at designing a protocol under a distributed network to achieve an asymptotic convergence of the state of each agent｛xi（k）， i∊N｝according to the global objective in Eq.(13).

3.1.Distributed optimization algorithm based on fctitious play concept

In order to adopt and extend the fctitious play concept to establish a distributed optimization approach,frst,the empiricalfrequency willbe extended to the continuous domain.Second,based on the global objective and local empirical frequency,a local strategy evaluation function for agent i will be established.Third,an optimal strategy for agent i will then be decided for next iteration process.

3.1.1.Empirical frequency

In order to adopt the fctitious play concept for a continuous distributed problem,a distribution function is adopted to model the empirical frequency build up by each agent for its counterparts.

Consider the strategy domain Uifor every agent i is continuous and convex.Agent i will model the strategy adopted by its opponent j at time k as a Gaussian distributionThe empirical frequency of agent i for its counterpart j at time k is defned as）.If the strategy agent j plays in time k+1 is

the empirical frequency eji（k）is updated as

with

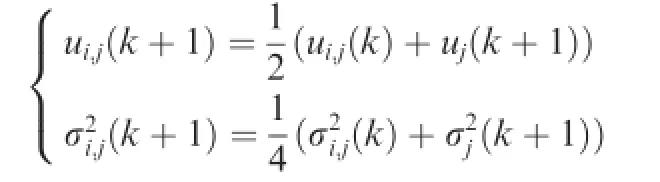
and the distribution function for）is denoted as fi（μj（k））.

Every agent i∊N willestablish its localempiricalfrequency at time k for all its opponents asDuring each game,agent i willnotonly share state information but also empirical frequency with its neighbours and update with the protocol given in Eq.(15).

3.1.2.Optimization

Based on the updating and sharing protocols for the empirical frequency,the cost for strategyμi∊Uiunder empirical frequencyis calculated by

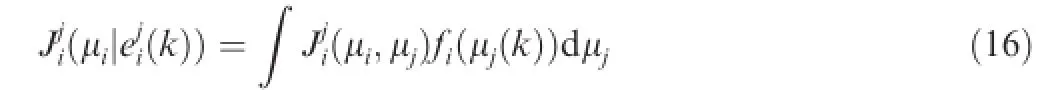
for a two agents game problem.

For the distributed optimization problem as suggested in Eq.(13),agent i will establish its empirical frequency for all its opponents as ei（k）=｛fi（μ1（k）），...，fi（μi-1（k）），fi（μi+1（k）），...，fi（μn（k））｝.Under the empirical frequency ei（k）,the cost for state xiis derived as

with xi∊Ui.

In every game,agent i will always search for the strategy∊Uithat yields the lowest cost for Eq.(17)under current empirical frequency as

and update xi（k+1）=.

The cost function Ji（μi|ei（k））for strategyμiunder the local empirical frequency ei（k）is different from the local cost function Ji（μi，μ-i）as discussed in Eq.(7).The empiricalfrequency based cost function Ji（μi|ei（k））is a constructed function based on the localempiricalfrequency ei（k）and the globalcost function Jg（x1，x2，...，xn）,while the localcost function Ji（μi，μ-i）is a predefned function based on the current strategies from agents which are accessible to agent i under a certain network topology.In this sense,without information from others,the local cost function cannot be verifed,while agent i can still make decision based on its empiricalfrequency and Ji（μi|ei（k））.

3.2.Convergence analysis and remarks

Defnition 2 suggests that for every iteration,if agent i’s strategy is selected from theε-dominate strategy domain,this algorithm is consistent with adaptive learning procedure.For the distributed optimization algorithm introduced in the previous section,the proposed algorithm suggests that agents will always adopt strategies that yield lowest cost based on their current empirical frequency.In this sense,the proposed distributed optimization algorithm is an adaptive learning process.According to Lemma 1,the sequence of state for each agent｛xi（k），i∊N｝follows the proposed distributed optimization algorithm will converge to a pure Nash equilibrium x*provided that the distributed problem Eq.(14)exists one.

Remark1.From the updating protocolas defned in Eq.(15), the memory sizeis defned as that agent i will only record the most recentstrategies of its opponent j as

Remark2.Since agents in learning game theory have no prior knowledge concerning their opponents,both the empiricalfrequency and strategies concerning their opponents are modelled as Gaussian distribution on（-∞，+∞）.

4.Application to consensus problems

In this section,the theoreticaldevelopments proposed in previous sections will be illustrated with two typical consensus problems.Based on the problem requirements,the two problems will frstly be modelled as distributed optimization problems and the proposed algorithm will be adopted for solving them.The frst problem is a distributed averaging problem and the second problem is a rendezvous problem,and in which,every agent is modelled as a UAV with unicycle model. The simulation result concerning the two problems willbe presented and discussed in the next section.

4.1.Distributed averaging problem

Consider there exist n agents with their initial states are not equal to each other and the sum of their states equals to l＞0.The state domain for each agent is continuous,convex and bounded as Ui=（0，l］， ∀i∊N.The inter-agent connection is distributed,i.e.the network topology is not a fullgraph. The mission requirement is to design a distributed protocol to let the state of every agent reach a consensus.For this typical consensus problem,the global cost function is designed as

where xiand xjrepresent the states of agent i and agent j, respectively.By analyzing the cost function,the only equilibrium is achieved when xi=xj， ∀i，j∊N.

Based on the problem requirement,the local cost function can be designed as

with the neighbour set for each agent is defned based on the distributed and connected network topology.

From the defnition of the local cost function,the designed game is a bounded potentialgame24with its potentialfunction as the global cost function Eq.(19).According to the properties of a potential game,the designed game is guaranteed topossess a Nash equilibrium and the equilibrium for local cost function Eq.(20)is consistent the global objective Eq.(19).

Provided that the empirical frequency）is defned as a Gaussian process as,the cost for a strategy xi∊Uiis

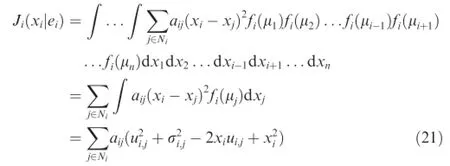
where the time k is ignored for concision.

Because of the assumption of myopic for agents and the convexity of the local cost function,the optimal strategyfor agent i based on its empirical frequency is derived from

which is the weighted average of the mean values of agent i’s empirical frequency.

Further,if the weight a admits

ij=1 and the memory size for agent i’s empirical frequency equals 1,which impliesthen

which is consistent with the discrete consensus protocol.3

Lemma2.Every bounded potentialgame has approximate fnite improvement property(AFIP).24

Theorem1.The algorithm proposed in this section willconverge with fnite iteration steps for the consensus problem as suggested in Eq.(19)and will only converge to the consensus state as

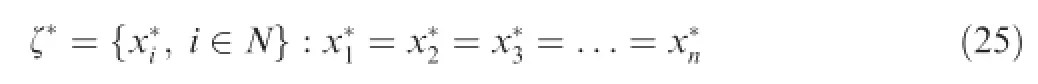
Proof.The proof of this theorem is based on the proof of the following two statements:

(1)The sequence of this algorithm will converge with fnite iteration steps

(2)If the algorithm converges,it will only converge to the consensus state as suggested in Eq.(25).

[Proof of Convergence I]As discussed in Section 3.2 and Lemma 2,with the proposed distributed optimization algorithm,the problem will converge with fnite iteration steps.

[Proof of Convergence II]Assume the algorithm will converge to certain stateζandζ≠ζ*,whereζ*is the equilibrium state as suggested in Eq.(25).Since the network topology in this problem is distributed and connected,there must exist agent j∊Nisuch that

Sinceζis the state of convergence,according to the empiricalfrequency updating protocol and Defnition 4,the empirical frequency for agent i and agent j will be

Therefore,according to Eq.(23),the new updating process is

Since xi≠xjthe updated stateζ＇=｛x＇

1，x＇2，...，x＇

n｝is not equal toζ,according to the defnition of convergence as Defnition 4,the assumption does not hold.Therefore,if the algorithm converges,it will only converge to the consensus state as Eq.(25).

4.2.Rendezvous problem for UAVs

A rendezvous problem is a typical multi-agent cooperation problem.For a rendezvous mission,multiple agents are usually required to arrive a rendezvous point through communication with each other under a distributed network topology.A rendezvous problem can be related to various application domain.The authors30–32considered the planning of threatavoiding trajectories for agents for a rendezvous mission in a hostile environment.In this section,without further complicated the discussion,a simple rendezvous problem will be considered and the problem will be handled with the proposed distributed optimization algorithm as discussed in previous sections.

Assume there are n agents located randomly on a 2-dimensioal(2D)plane,and the inter-agent communication is undirected and distributed.Each agent i can only communicate with its neighbour j∊Ni.The model for each agent follows the defnition of a unicycle model as

where V is the constant speed for every agentandωiis the control input.

The rendezvous problem requires agents to gather to the same location on the 2D plane.The controllers for agents are designed based on their own empirical frequency.The rendezvous mission does not require UAVs arrive the same location at the same time.The inter-UAV communication happens on a predefned time interval,and vehicles willre-adjust their control inputs whenever information update is available.For this rendezvous problem,the globalcost function is designed as

with

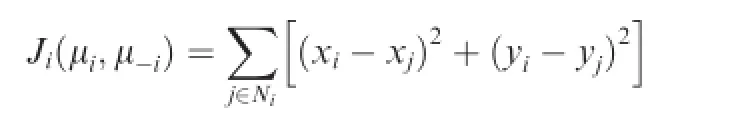
whereμi=（xi，yi，θi）is the state of agent i.

Based on the discussion of the distributed optimization algorithm in previous sections,each agent i will establish its local empirical frequencybased on the information from its neighbours.Each entry of the empirical frequencyis the estimation for the state of another agent,ith bothare Gaussian pro-respectively. For a strategysince the global cost function only involves the state ofthe cost of the strategy based on the local empirical frequency is

By analyzing Jg（μ1，μ2，...，μn）and｛Ji（μi，μ-i），i∊N｝in Eq.(31),the designed problem is consistent with a potential game as defned in Defnition 5,and thus,the equilibrium for｛Ji（μi，μ-i），i∊N｝is consistent with the global objective. Therefore,the cost function for the strategyμiof agent i can be simplifed as

With the support of Eq.(33),the optimal control problem is design as

By solving this optimal control problem,the control input and the trajectory for each agent can be obtained for the rendezvous mission.

5.Simulation results

In this section,based on the analysis of the two consensus problems in the previous section,corresponding simulations are conducted to illustrate the theoretical developments.

5.1.Simulation for distributed averaging problem

The simulation for the distributed averaging problem is conducted to illustrate the infuence of neighbour numbers and memory size on convergence effciency.The number of neighbours for each agent is the same.The weights aijare constant and equal to each other.Every agent can only communicate with its most adjacent agents.The updating protocol adopted in the simulation follows Eq.(15)with the variance values for distribution functions equal 0.

Table 1 and Fig.1(a)demonstrate the infuence of number of neighbours on the algorithm convergence rate.The memory size in this case is infnite,which implies that each agent will record the whole strategy profle for its counterparts.

From the simulation results,it is apparent that the convergence effciency will increase if the number of neighbours for each agent is increased,which is coherent with the fundamental consensus theory.33

Table 1 and Fig.1(b)demonstrate the infuence of memory of the empirical frequency on the algorithm convergence rate. In Table 1,the column‘Infnite memory size’’represents the case that agents will take all strategies adopted by their counterparts into consideration to make their own decision,while‘Memory size 2’and‘Memory size 3’columns represent agents will only use the most recent 2 or 3 information to estimate their opponents’strategy patterns.

In order to make the simulation result more clear for demonstration,the information updating process for only one agent is demonstrated in Fig.1(b).The blue line represents the infnite memory case;the red line represents the case in which the memory size of the empirical frequency equals 2; the green line represents the memory size 3 case.

The result demonstrates that for the network that each agent has less neighbours,the decrease of memory size will improve the performance greatly.However,under network topologies that each agent has more neighbours,there is no clear pattern to describe the infuence of memory on the performance of convergence.

5.2.Simulation for rendezvous problem with multiple UAVs

The simulation for the rendezvous problem is conducted to demonstrate the designing procedure of a distributed multiagent cooperation mission based on the distributed optimization algorithm proposed before.In the simulation,5 unicycle model based vehicles are considered with constant velocity V=10 m/s.The vehicles are distributed on the 2D plane at points[1 km,3 km],[3 km,7 km],[9 km,10 km],[10 km, 4 km]and[6 km,2 km].

In this problem,the inter-vehicle collision and obstacle avoidance are not considered for simplicity.The inter-vehicle communication is distributed,and each vehicle can only communicate with its 2 most adjacent neighbours under an undirected network topology.The communication is assumed to happen every 10 s after the mission start,and communicationfailure is not considered.The optimization will be terminated when the global cost is smaller than a predefned threshold T,and in the simulation,the threshold is set as T=0.1.The general pseudo-spectral optimization software(GPOPS)34is adopted for the optimal control problem.

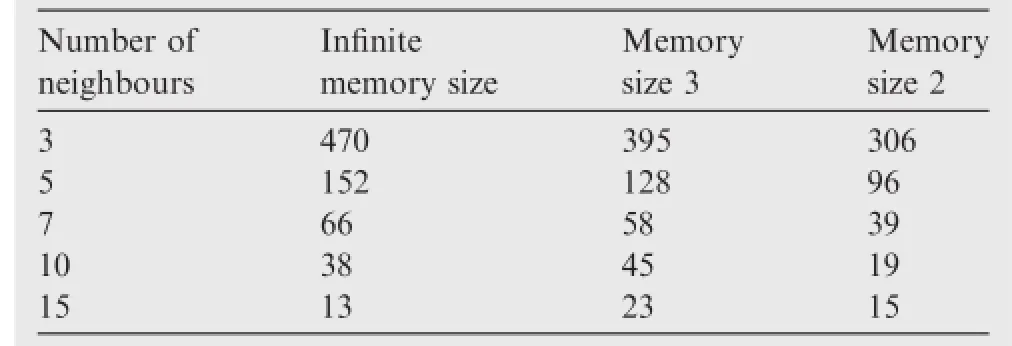
Table1 Simulation results for the distributed averaging problem.

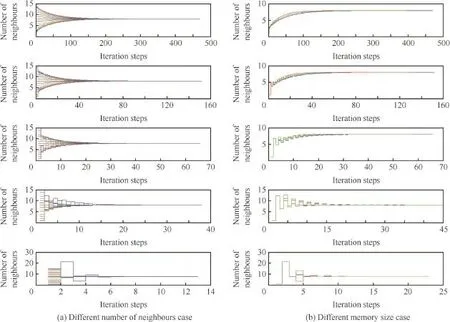
Fig.1 Simulation for distributed averaging problem.

The trajectories for the vehicles are demonstrated in Fig.2(a),and corresponding global cost function convergence result with regard to time is illustrated in Fig.2(b).The convergence of the state x and y for each vehicle are demonstrated in Fig.3(a)and(b)separately.Fig.4(a)shows the simulation result of the stateθ.The designed controller signal is as demonstrated in Fig.4(b).

The simulation demonstrates that the designed controller based on the distributed optimization algorithm proposed in the previous section can achieve the rendezvous mission requirement.

Fig.2 Simulation results of trajectory for each vehicle and global cost.

Fig.3 Simulation results of states x and y.

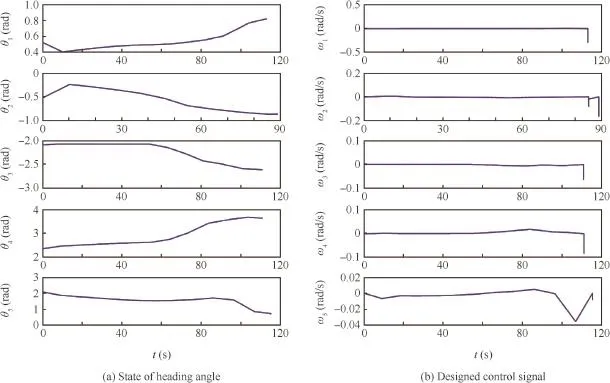
Fig.4 Simulation results of heading angleθand control signalω.

6.Conclusions

(1)A distributed optimization algorithm is designed based on the fctitious play concept.The algorithm assumes agents analyze past observations as ifbehaviours oftheir competitors were stationary,and by learning from the strategy patterns of their opponents,agents will decide their own optimal strategies.

(2)The designed distributed optimization algorithm ensures the algorithm autonomy and robustness through the learning behaviour of each agent.

(3)Convergence of the proposed algorithm is proven under game theory framework to guarantee the algorithm will converge to a Nash Equilibrium provided that the original problem design exists one.

(4)By introducing and analyzing the two typical consensus problems with the proposed distributed optimization algorithm,this paper provides a guideline for multiagent cooperation problem design under game theory framework.

(5)Simulation results are provided to demonstrate that the designed game model for the distributed multi-agent cooperation problems can ensure global cooperation among myopic agents.

Acknowledgements

This work is funded by China Scholarship Council(No. 201206230108)and the Natural Sciences and EngineeringResearch Council of Canada Discovery Grant(No.RGPIN 227674).

1.Herna´ndez JZ,Ossowski S,Garcıa-Serrano A.Multiagent architectures for intelligent traffc management systems.Transp Res Part C Emerg 2002;10(5–6):473–506.

2.Abreu B,Botelho L,Cavallaro A,Douxchamps D,Ebrahimi T, Figueiredo P,et al.Video-based multi-agent traffc surveillance system.Proceedings of the IEEE intelligent vehicles Symposium IV 2000;Oct3–5;Dearborn,MI.Piscataway,NJ:IEEE;2000.p.457–62.

3.Ren W,Beard RW.Distributed consensus in multi-vehicle cooperative control:theory and applications.London:Springer-Verlag; 2008.

4.Ren W,Beard RW.Consensus seeking in multiagent systems under dynamically changing interaction topologies.IEEE Trans Autom Control 2005;50(5):655–61.

5.Remagnino P,Tan T,Baker K.Multi-agent visualsurveillance of dynamic scenes.Image Vis Comput 1998;16(8):529–32.

6.Orwell J,Massey S,Remagnino P,Greenhill D,Jones GA.A multi-agent framework for visual surveillance.Proceedings of international conference on image analysis and processing;1999 Sept27–29;Venice,Italy.Piscataway,NJ:IEEE;1999.p.1104–7.

7.Ivanov YA,Bobick AF.Recognition of multi-agent interaction in video surveillance.Proceedings of the seventh IEEE international conference on computer vision;1999 Sept 20–25;Corfu, Greece.Piscataway,NJ:IEEE;1999.p.169–76.

8.Janssen M,de Vries B.The battle of perspectives:a multi-agent model with adaptive responses to climate change.Ecol Econ 1998;26(1):43–65.

9.Olfati-Saber R.Flocking for multi-agent dynamic systems:algorithms and theory.IEEE Trans Autom Control 2006;51(3):401–20.

10.Jadbabaie A,Lin J,Morse AS.Coordination of groups of mobile autonomous agents using nearest neighbor rules.IEEE Trans Autom Control 2003;48(6):988–1001.

11.Vicsek T,Cziro´k A,Ben-Jacob E,Cohen I,Shochet O.Noveltype of phase transition in a system of self driven particles.Phys Rev Lett 1995;75(6):1226.

12.Zhang F,Leonard NE.Cooperative flters and control for cooperative exploration.IEEE Trans Autom Control 2010;55(3): 650–63.

13.Zhang F,Fiorelli E,Leonard NE.Exploring scalar felds using multiple sensor platforms:tracking level curves.Proceedings of 2007 46th IEEE conference on decision and control;2007 Dec 12–14;New Orleans,LA.Piscataway,NJ:IEEE;2007.p.3579–84.

14.Saber RO,Murray RM.Consensus protocols for networks of dynamic agents.Proceedings of the American control conference; 2003 Jun 4–6;Pasadena,CA.Piscataway,NJ:IEEE;2003.p. 951–6.

15.Olfati-Saber R,Murray RM.Consensus problems in networks of agents with switching topology and time delays.IEEE Trans Autom Control 2004;49(9):1520–33.

16.Fax JA.Optimal and cooperative control of vehicle formations [dissertion].California:California Institute of Technology;2001 [dissertation].

17.Fax JA,Murray RM.Information fow and cooperative controlof vehicle formations.IEEETrans Autom Control2004;49(9):1465–76.

18.Kraus S.Negotiation and cooperation in multi-agent environments.Artif Intell 1997;94(1–2):79–97.

19.Semsar-Kazerooni E,Khorasani K.Multi-agent team cooperation:a game theory approach.Automatica 2009;45(10):2205–13.

20.Li N,Marden JR.Designing games for distributed optimization. Proceedings of 2011 50th IEEE conference on decision and control and European control conference;2011 Dec 12–15;Orlando, FL.Piscataway,NJ:IEEE;2011.p.2434–40.

21.Li N,Marden JR.Designing games for distributed optimization. IEEE J Selected Top Signal Process 2013;7(2):230–42.

22.Lin ZJ,Liu HHT.Consensus based on learning game theory. Proceedings of the 6th IEEE Chinese guidance navigation and control conference;2014 Aug 8–10;Yantai,China.Piscataway, NJ:IEEE;2014.

23.Milgrom P,Roberts J.Adaptive and sophisticated learning in normalform games.Games Econ Behav 1991;3(1):82–100.

24.Monderer D,Shapley LS.Potential games.Games Econ Behav 1996;14(1):124–43.

25.Shapley LS.A value for n-person games.1952 Mar.Report No.: AD604084.

26.Gopalakrishnan R,Nixon S,Marden JR.Stable utility design for distributed resource allocation[Internet];2014[cited 2014 Jun]. Available from:＜http://ecee.colorado.edu/marden/fles/cdc2014. pdf＞.

27.Marden JR,Shamma JE.Game theory and distributed control. Handbook of game theory,vol.4.Forthcoming.

28.Wolfowitz J.Products of indecomposable,aperiodic,stochastic matrices.Proc Am Math Soc 1963;14(5):733–7.

29.Cao YC,Yu WW,Ren W,Chen GR.An overview of recent progress in the study of distributed multi-agent coordination. IEEE Trans Industr Inf 2013;9(1):427–38.

30.McLain TW,Chandler PR,Rasmussen S,Pachter M.Cooperative control of UAV rendezvous.Proceedings of the American control conference;2001 Jun 25–27;Arlington,VA.Piscataway,NJ: IEEE;2001.p.2309–14.

31.McLain TW,Chandler PR,Pachter M.A decomposition strategy for optimalcoordination of unmanned air vehicles.Proceedings of the American control conference;2000 Jun;Chicago,Illinois.Piscataway,NJ:IEEE;2000.p.369–73.

32.McLain TW,Beard RW.Trajectory planning for coordinated rendezvous of unmanned air vehicles.2000.Report No.:AIAA-2000-4369.

33.Olfati-Saber R,Fax JA,Murray RM.Consensus and cooperation in networked multi-agent systems.Proc IEEE 2007;95(1):215–33.

34.Rao AV,Benson DA,Darby C,Patterson MA,Francolin C, Sanders I,et al.Algorithm 902:GPOPS,a MATLAB software for solving multiple-phase optimal control problems using the gauss pseudospectral method.ACM Trans Math Softw 2010; 37(2):22:1–22:39.

LinZhongjiereceived his B.S.degree from the school of electronic information and electrical engineering of Shanghai Jiao Tong University and M.S.degree from the school of aeronautics and astronautics of Shanghai Jiao Tong University.He is currently a Ph.D. candidate at the University of Toronto Institute for Aerospace Studies (UTIAS).His main research interests are multi-agent cooperation problems,distributed optimization,game theory and task assignment domain.

LiuHughhong-taois a professor at the University of Toronto Institute for Aerospace Studies(UTIAS),Toronto,Canada,where he also serves as the Associate Director,Graduate Studies.His research work over the past several years has included a number of aircraft systems and control related areas,and he leads the‘Flight Systems and Control’(FSC)Research Laboratory.

Received 23 July 2014;revised 15 September 2014;accepted 2 November 2014 Available online 26 December 2014

*Corresponding author.Tel.:+1 416 667 7928.

E-mail address:liu@utias.utoronto.ca(H.h.-t.Liu).

Peer review under responsibility of Editorial Committee of CJA.