运用正弦扫频实现电动振动台模型的频域辨识

严侠，李晓琳，胡勇

（中国工程物理研究院 总体工程研究所，四川 绵阳 621900）

运用正弦扫频实现电动振动台模型的频域辨识

严侠，李晓琳，胡勇

（中国工程物理研究院 总体工程研究所，四川 绵阳 621900）

目的研究以电动振动台为典型设备的相关振动试验装置的频域辨识技术。方法通过分析电动振动台数学模型，采用正弦扫频试验方法，进行全频带振动台空台面正弦扫频，并对所获得的时域正弦扫频数据进行频谱分析，进而获得系统的频率数据，再运用复数域上的最小二乘拟合算法，完成振动台模型传递函数的辨识。结果通过某型电动台空台面试验，对一组实测数据进行辨识，辨识出的电动振动台模拟与真实模拟一致。结论通过该方法并合理选取模型结构，能够很好地辨识出振动试验装置的模型。

电动振动台；正弦扫频；传递函数；最小二乘；频域辨识

振动环境试验是产品研发中的重要环节，通过试验可以了解或评价结构对振动环境的适应性，为产品设计修改提供参考，为产品的定型、验收提供依据。电动振动台是振动环境试验的主设备，开展电动振动台模型辨识研究，将有助于深入了解电动振动台系统的内部结构和工作原理，准确掌握其特性与性能，并将有利于更好地设计振动环境试验，维护设备。另外，建立振动台模型，对开展振动控制技术研究和振动试验仿真研究也是非常有意义的。

辨识工作早在19世纪70年代就已开始，许多经典的辨识方法都是从测量时域数据来辨识系统模型，如最小二乘（LG）[1]、广义最小二乘（GLS）[2]，辅助变量法（IV）等[3]。前10多年里，对于线性定常系统使用频域数据辨识模型应用也逐渐开始，尤其在一些容易获得周期激励信号的应用领域（如振动分析，机械伺服系统等[4—6]）。采用正弦扫频信号作为系统的激励，获取系统频域数据，已经在工业中有所应用（如Abdullah Al Mamun，2002[7]）。在一些工业应用领域（如振动分析）常采用频域方法，运用频域辨识，可以直接辨识系统的传递函数。通过进行系统的频谱分析，通常可以获得一个系统的非参数模型，再使用Levy法[8]等，便可以得到系统的传递函数。

电动振动台辨识工作中，可采用常用的正弦扫频振动试验而不需要再单独设计试验，然后对获得的输入、输出数据进行频谱分析，便可获得系统的非参数模型。再通过Levy法等复数域内的曲线拟合法（文中采用最小二乘拟合法），便能够得到系统的传递函数。

1 电动振动台系统模型分析

由于电动振动台是一个很复杂的电力学系统，要精确地建立其模型是十分困难的，因此建立模型时要忽略其非线性和时变的因素。电动振动台模型主要由力学和电学模型组成。

电动振动台的力学模型如图1a所示，首先，振动台通常使用柔性底座（KB）（比如钢螺旋簧或者空气弹簧），允许整个振动台垂向运动，把振动台体（MB）的振动与建筑物地面隔离。其次，电枢组件和台体（MB）之间也是采用柔性连接（ks），明显地形成了弹簧/质量/阻尼振动系统。最后，电枢组件（MT，MC）被当作弹性体而不是刚体，在模型中把动圈（MC）和台面（MT）当作是用弹簧（Kc）和阻尼连接起来的两个分离质量。当安装有试验对象（MD）时，还会增加质量弹簧系统。这里主要是辨识振动台模型，把试验对象简化为一个和电枢组件一起运动的质量。

振动台的电学模型如图1b所示，这里必须考虑电枢的电阻和电感。线圈电阻R定义了一个在振动台输入端子处（测量）表现出的最小阻抗。这个电阻随着温度的升高有所增加，随着频率的增大有轻微增加（由于集肤效应）。线圈的电感与铁磁极件强烈耦合，振动台振动时引入反生电动势eback。整个电学回路，由振动台的前级（功率放大器）提供外部电压E和电流I来驱动电学回路。

图1 电动振动台Fig.1 The electric dynamic shaker

振动台的力学部件和电学部件是互相耦合的，机械系统被与电流成比例的力激励，而电路被与机械速度成比例的内部电压（反电动势）所激励。

整个系统的微分方程组表示为：

系统工作中，由于阻抗受温度和频率的变化而变化。同时，振动台的前级功率放大器作为其驱动也与电动台的电学模型耦合在一起的，组成了一个复杂的带有非线性和时变因素的高阶系统。在研究过程中，忽略阻抗慢变，并假定功率放大器是线性定常系统，振动台系统可以看成是一个高阶线性模型。以振动控制器驱动信号为振动台系统的输入，加速度传感器响应为系统输出，其系统的传递函数为，

2 正弦扫频信号的频谱分析

通过系统全频带的正弦扫频振动试验，可以获得系统输入、输出正弦扫频信号数据。为了进行下一步的频域辨识，需要将时域数据处理成辨识所需要的频域数据，即{wi，G（jwi）}。

正弦扫频信号的频谱分析方法很多，但要真实和快捷地分析出信号的当前频率、幅值和相位却并不容易。这里利用了FFT分析整周期信号无泄漏的优点，采用对信号进行整周期截取的方法来实现正弦扫频信号的频域分析。

频域分析分析方法如图2所示，首先对正弦扫频信号进行滤波，去除高频干扰，然后以驱动信号作参考截取信号的1个整周期，最后对该整周期信号进行FFT分析，从而获得系统当前的{wi，G（jwi）}。采集到的时域正弦扫频信号（低频段）如图3a所示，经过数字滤波器后的信号如图3b所示，截取的整周期信号如图3c所示。

图2 正弦扫频数据分析流程Fig.2 The flow chart of sine-sweep signal data analysis

图3 正弦扫频信号Fig.3 The sine-sweep signal

对于整周期信号分析的好处在于，信号不需要加窗，分析的频谱为单一的谱线，在扫频速率较低，截取的整周期可以认为是一个标准的正弦信号，因此频谱分析的效果很好。对驱动信号和输出信号的频谱分析（该信号在低频5 Hz附近其谱线靠近起始端）如图4所示，取其一次谐波即可得出当前信号的幅值、相位及频率。从而也就得到了系统频域辨识数据{wi，G（jwi）}。

图4 信号整周期频谱Fig.4 The whole period response signal spectrum

一个动力学系统的传递函数为：

可以从频率响应数据{wi，G（jwi）}（i=1，…，N）来进行线性定常系统的传递函数模型的估计。

令：

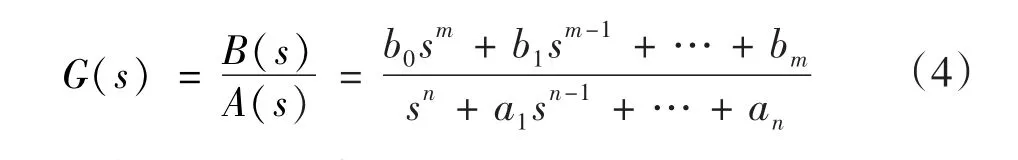
在任意某个频率wk上有：

最小二乘参数估计目标是极小化误差标准J函数：

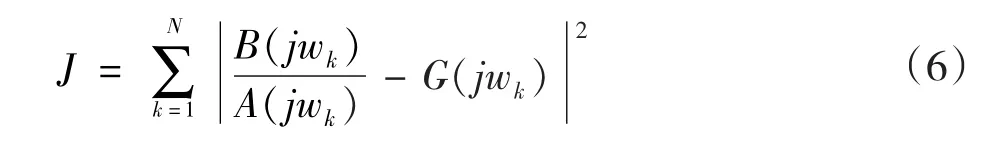
这里存在一个非线性估计最小二乘问题，重写上面的方程为：

或者：

3 传递函数的最小二乘拟合方法

式中：θ表示参数向量，θ=［b0，b1，…bm，a1，a2，…an］T。如果系统的频率响应在不同的频率点上被测量，能获得N组上面的方程：

式中：np是参数的个数，为n+m。

为了利用最小二乘估计参数向量，最小化下面的目标函数：

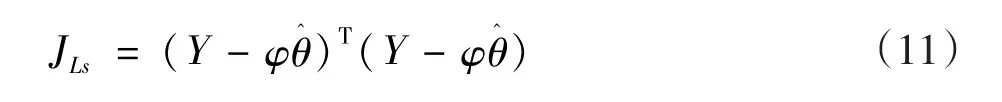
最小二乘参数估计给出为：

该最小二乘拟合法是一个很常用的拟合算法，这里它的误差函数包括了（jwk）n项。当频率增加时，会使误差J函数增大，关于复数域上的曲线拟合问题，有多种改进算法[9—12]，将可以克服曲线拟合精度的问题。

4 应用

以辨识某型电动振动台空台面模型为例。辨识中，利用振动控制器作振动台空台面正弦扫频振动试验，频率范围为5～3000 Hz，试验加速度为10g，扫频速率为1 oct/min，加速度传感器灵敏度为100 mV/g。同时采集振动台系统的输入、输出数据，取采样频率为40 kHz，测量系统的信噪比为2%。

根据系统辨识数据，运用最小二乘拟合传递函数，经过频谱分析后的振动台空台面系统的幅频特性和相频特性如图5所示。

图5 振动台空台面的频率特性Fig.5 The frequency characteristics of the electrodynamic empty shaker

由于在辨识之前必须选定模型的结构，从幅频特性中可以看出，整个频段具有2个峰，低频段上存在一个一阶微分环节。选取了4组模型结构，见表1。同时给出了极小化误差函数J的值。

从表1可以看出，在结构选择n=6，m=5时，J值取最小，此时辨识出来的系统传递函数效果最好，该结构也基本吻合于振动台的数学模型式（1）。如图6所示，辨识出来的系统幅频和相频特性都拟合得很好。按照10 kHz的采样频率离散化后的传递函数模型如下：

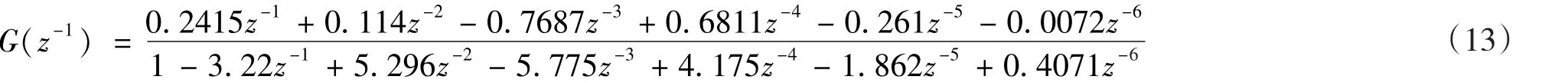
表1 不同模型结构的辨识情况Table 1 The iderutify situations of different model stueture

图6 辨识传函频率的拟合情况Fig.6 Fitting results of the identification frequency of the transfer function

5 结论

文中利用正弦扫频信号建立电动振动台的数学模型，在此基础上，确认了频域传递函数的大致阶数。通过对扫频数据的频谱分析进行研究，选择用不加窗的整周期频谱分析方法。利用频域数据拟合的方法建立了电动振动台的参数化模型。通过对一组实测数据进行辨识，辨识出的电动振动台模拟与真实模拟一致。

[1] LJUNG L，SÖDERSTRÖM T.Theory and Practice of Recursive Identification[M].Cambirdge：MIT Press，1983.

[2] SÖDERSTRÖM T，STOICA P.System Identification[M].Englewood Cliffs：Prentice Hall International，1989.

[3] JOHANSSON R，System Modeling and Identification[M].Englewood Cliffs：Prentice Hall，1993.

[4] LJUNG L.SomeResultson Identifying Linear Systems Using Frequency Domain Data[C]//In proceedings of 32nd Conference on Decision and Control.San Antonio，1993.

[5] SCHOUKENS J，PINTELON R.Identification of Linear System，a Practical Guideline to Accurate Modeling[M].London：Pergamon Press，1991.

[6]VRIES de D，VAN den H of PMJ.Frequency Domain Identification with Generalized Orthonormal Basis Functions[J].IEEE Trans Autom Contro，1998，43（5）：656—659.

[7] ABDULLAH A M，LEE T H.Frequency Domain Identification of Transfer Function Model of a Disk Drive Actuator[J].Mechatronics，2002（12）：563—574.

[8] LEVY E C.Complex-curve Fitting[J].IRE Trans on Auto Control，1959，4（1）：37—43.

[9]MCCORMACK A S，GODFREY K R.Rule-based Auto Tuning Based on Frequency Domain Identification[J].IEEE Trans Control Syst Technol，1998，6（1）：43—61.

[10]PINTELON R，GUILLAUME P，ROLAIN Y，et al.Parametric Identification of Transfer Function in the Frequency Domain-a Survey[J].IEEE Trans on Autom Control 1994，39：2245—2260.

[11]ROLAIN Y，PINTELON R，XU K Q，et al.Best Conditioned Parametric Identification of Transfer Function Models in the Frequency[J].IEEE Trans on Autom Control，1995，40（11）：1954—1960.

[12]顾启泰，刘学斌.Levy方法的改进[J].航空学报，1997，18：735—738.GU Qi-tai，LIU Xue-bin.Improve Levy Method[J].Aeronautics 1997，18：735—738.

Application of the Sine-sweep Test in Model Frequency Identification for a Electrodynamic Shaker

YAN Xia，LI Xiao-lin，HU Yong
（Institute of Systems Engineering，China Academy of Engineering Physics，Mianyang 621900，China）

ObjectiveTo study the frequency domain identification technology for vibration test equipment,using the electric dynamic shaker as a typical device.MethodsFirstly,the mathematics model of the electrodynamic shaker was analyzed,secondly,the sine-sweep test was used for whole-frequency sine sweep of the empty vibration table,and the sine-sweep signal data acquired was subjected to frequency spectrum analysis.So the frequency data of the electrodynamic shaker system was acquired.Finally,the least squares complex-curve fitting algorithm was used to accomplish the identification of the transfer function for the vibration table model.ResultsThrough test with an empty electrodynamic shaker,a group of measured data was identified,and the electrodynamic shaker simulation mode identified was consistent with the real simulation.ConclusionUsing this method,in combination with matching the structure of the shaker model,the model of the vibration test equipment could be well identified.

electrodynamic shaker；sine-sweep；transfer function；least squares；frequency identification

2014-12-21；

2015-03-05

严侠（1977—），男，四川人，硕士，高级工程师，主要研究方向为振动控制、振动试验技术等。

Biography：YAN Xia（1977—），Male，from Sichuan，Master，Senior engineer，Research focus：vibration control&vibration test technology.

10.7643/issn.1672-9242.2015.02.010

TJ01；O324

A

1672－9242（2015）02－0044-05

2014-12-21；

2015-03-05