基于数值积分的物理学Flash课件
彭 亮
(武汉铁路职业技术学院,湖北 武汉 430205)
0 前言
物理学是一门实验科学,单纯从数学角度来记忆公式是无法深入理解物理规律的。在物理教学过程中,传统的以粉笔和黑板作为媒介的教学方式比较死板,通过借助计算机技术,将物理运动过程制作成多媒体课件,形象、直观的展示出来,能够加深学生对物理规律的感性认识,从而提高教学的效果。
Flash是常用的动画软件之一,具有使用方便、动画效果好的优点,最为重要的是内置一套Action Script编程语言,能够通过程序的方式实现其他软件难以实现的动态效果。在物理学课件的制作过程中,传统静态动画制作方式过程繁琐,而且难以精确的再现物理运动过程。借助Flash提供的Action Script编程语言,制作过程得到了简化,还具有精确、通用性强的优点。
1 Flash中实时展现物理过程的方法
1.1 基于运动方程的方法
Flash采用帧的方式运行,通过改变图形在不同帧的位置、大小等属性来实现动画的效果,属于时间离散的过程,而真实的物理运动过程则是时间连续的。为了在Flash中精确的再现物理运动过程必须对时间连续的过程进行离散化。
物理运动过程可以由运动方程来描述,例如:
运动方程直接给出了位置与时间的关系,通过在每帧中使用方程计算出位置坐标就能再现运动过程。
这种方法精准度高,只有计算过程中的舍入误差,且误差不会累积。但该方法必须事先求出运动方程,而且不同场景的运动方程差异极大,所以通用性不是很好。
1.2 采用数值积分的方法
由于基于运动方程的方法不够灵活,通用性差,有必要直接从影响物体运动的物理规律出发,寻找一种通用的方法。
根据牛顿定律可知:物体的运动过程由初始状态(位置、速度)以及受到的力决定,而日常中出现的力可以看成和时间、物体位置和速度有关的函数,因此可以用以下微分方程来表示物体运动过程。

在物体的初始位置和速度已知的情况下,通过数值积分的方法,计算出下一帧的位置和速度,然后以此类推,也能够再现物体运动过程。这种方法通用性较好,但精度比采用运动方程的方法要差,因为使用数值积分递推计算位置和速度,不仅存在舍入误差,还有数值积分方法带来的截断误差,且误差会累积。不过通过采用高精度的计算方法,误差能做到可以接受的程度。
2 数值积分过程
2.1 欧拉方法
首先将式1改写为以下形式

采用欧拉方法求解上式的过程如下:

2.2 龙格库塔方法
采用龙格库塔方法求解式2的过程如下:
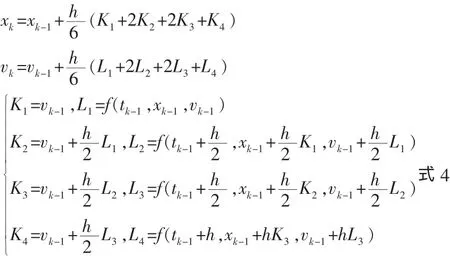
3 实例及性能分析
以斜抛运动为例,其运动过程可由以下微分方程描述:
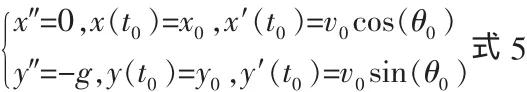
上述式子第一项描述水平方向的运动过程,第二项描述垂直方向的运动过程。
3.1 采用欧拉方法的程序

程序中sx表示水平方向的位置,vx表示水平方向的速度,sy表示垂直方向的位置,vy表示垂直方向的速度,t表示时间,h表示积分步长。方法caculateAccX和caculateAccY用于求取加速度,与式2中的函数 v′=f(t,x,v)对应。
3.2 采用龙格库塔方法的程序
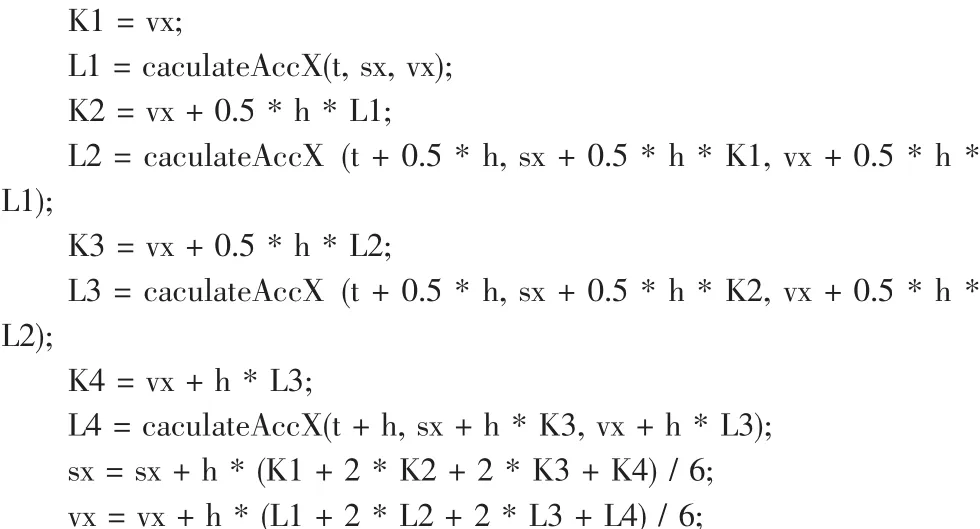
以上程序为水平方向的计算过程,垂直方向的计算过程与之类似,程序中的变量和函数与欧拉方法程序的变量和函数相同。可以看到龙格库塔法的计算过程要比欧拉方法复杂,接下来将会对两者的性能进行比对分析。
3.3 性能分析

图1
图1中为取h=0.2s时的运行结果,图中实线为运动方程表示的运动过程,+记号的点序列表示欧拉方法计算结果,×记号的点序列表示龙格库塔方法计算结果。可以看出欧拉方法在初段与运动方程的结果相近,但随着步数增加,误差越来越大,而龙格库塔法的误差几乎可以忽略。
4 结束语
本文介绍了基于数值积分的物理学Flash课件制作方法,给出了采用两种不同数值积分的实现过程,并对两者的性能进行比对,得出结论:欧拉方法计算过程简单,但误差较大,适合在步长较短且运行时间也比较短的场合使用,龙格库塔法计算过程复杂,但误差很小,适合在步长较长且运行时间也比较长的场合使用。
[1]陈誌敏.龙格-库塔法及其Mathematica实现[J].武汉工程职业技术学院学报,2006,18(2).
[2]黄晓红,胡振华.浅析龙格-库塔方法[J].黑龙江科技信息,2012(23).
[3]陆映红.基于物理学原理Flash行为动画的实现[J].广西民族学院学报,2005,11(4).

