运动目标的超前预测跟踪

左 韬

（武汉科技大学信息科学与工程学院，湖北 武汉430081）

0 前言

运动目标跟踪广泛应用在雷达、视频跟踪、无线激光通信、天文观测、航空摄影等领域，现有的运动目标跟踪方法一般都是在取得目标运动状态观测值的情况下，应用滤波方法得到状态的最优估计值，这种方法可以大幅度减小噪声对跟踪的影响，但却无法克服跟踪的滞后。在观测噪声影响不大的情况下，本文对运动目标的状态采取卡尔曼滤波先验预测，可提前一步预测目标的运动状态，跟踪执行机构可超前预测跟踪，从而克服跟踪的滞后。

1 目标运动模型

采用“当前”统计模型建立目标运动模型[1]，得到目标运动的状态描述。该模型用修正的瑞利分布来描述加速度的“当前”概率密度，本质上是非零均值时间相关模型。以x（t）表示目标的位置，表示目标的速度，表示目标的加速度，则状态向量为：

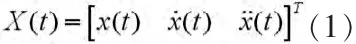
目标运动的“当前”统计模型非零均值状态方程表示为：

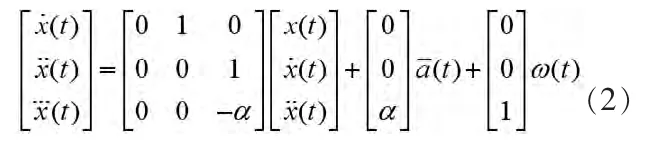
采样周期为T时的离散状态方程为

观测方程为

W（k）、V（k）为均值为0的离散高斯白噪声序列，当只有位置数据可直接观测时，H（k）=［1 0 0］。

采用“当前”统计模型描述目标的运动状态，符合机动运动的实际特性，能较好的反映目标机动范围和强度的变化，且响应速度快、跟踪精度高。

2 卡尔曼滤波预测

对运动目标建立当前“统计”模型状态方程和观测方程之后，由卡尔曼滤波[3]可得到目标运动状态的预测值和最优估计值，卡尔曼滤波由如下核心方程组成：

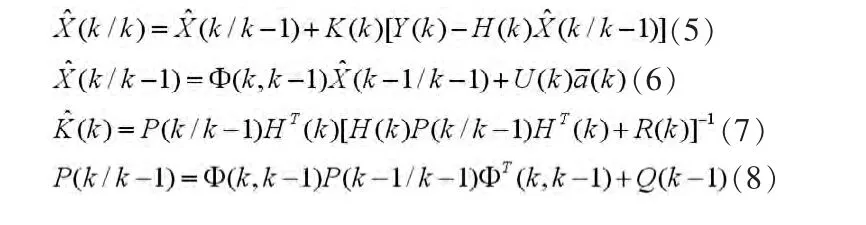
本文采用公式(6)实现对目标运动状态的超前一步预测，也就是由已知的运动状态预测下一时刻的运动状态，从而克服跟踪的滞后，超前预测值是一种先验预估，预测精度低于后验最优估值，虽然损失了精度，但可以提前一步预测跟踪，在跟踪滞后严重的情况下，可以取得较好的跟踪效果。

3 仿真分析

通过跟踪一个变速直线运动的目标来验证超前预测跟踪的性能。采样周期T为1秒，仿真时间130秒，目标初始位置在0.05km处，前100 s做0.05km/s的匀速运动，101-130 s做0.0005 km/s2的匀加速运动，观测噪声方差为0.02，均值为0。

对运动目标做位置跟踪，仿真结果如图1、2所示。图1为目标的真实位置与超前预测位置分布，可见预测位置非常逼近真实位置曲线，图2为目标位置的超前预测误差曲线，其均方根误差为0.0518 km。

图1 目标位置超前预测

图2 超前预测误差

4 结论

本文建立机动目标的当前统计运动模型，对运动目标采用卡尔曼滤波预测跟踪，可超前一步预测目标的运动状态，通过仿真分析，验证了对变速运动目标的位置超前预测有较好的跟踪效果，可有效克服跟踪的滞后。

［1］周宏仁，敬忠良，王德培．机动目标跟踪[M]．北京：国防工业出版社，1991.

［2］Jianfeng Wu,Gang Li,Fuzhou Ma.Research on target tracking algorithm using improved current statistical model[C]//2011 International Conference on Electrical and Control Engineering.2515-2517.

［3］Vinaykumar,M.,Jatoth,R.K..Performance evaluation of Alpha-Beta and Kalman filter for object tracking[C]//2014 International Conference on Advanced Communication Control and Computing Technologies.2014,1369-1373.