基于高频系数小波分析的高维蛋白质波谱数据特征提取

吴文峰，刘毅慧

（齐鲁工业大学信息学院，济南250353）

doi：10.3969/j.issn.1672－5565.2015.03.09

基于高频系数小波分析的高维蛋白质波谱数据特征提取

吴文峰，刘毅慧∗

（齐鲁工业大学信息学院，济南250353）

高维蛋白质波谱数据分析过程中，对于数据的特征提取一直是许多学者专注解决的问题。本文提出了一种基于高频系数的小波分析和主成份分析技术（Principal componentanalysis，PCA）的特征提取方法，首先采用小波分析技术对数据进行降噪，提取高频系数作为特征，之后用主成份分析技术进行降维。实验显示：本论文中提出的方法在8－7－02、4/3/02数据集上的实验识别率分别可以达到100％和99.45％，可以有效提高分类识别率。

波谱数据；高频；小波分析；主成份分析

自从波谱技术应用到生物医学研究领域开始，蛋白质波谱数据的分析研究便开始得到了迅速的发展。随着研究的广泛深入，研究过程中所获得的数据量变得越来越大，处理的难度也随之不断增加。如何有效的在众多数据中获取能表征蛋白质性质的重要属性维度，成为人们热衷的研究话题。目前人们使用比较广泛的降维和特征提取方法主要有小波分析［1］、主成份分析［2］、遗传算法［3］、T⁃test法［4］、Boosting［5］、模拟退火算法［6］等。

杨合龙等在对高通量SELDI⁃TOF质谱数据进行分析时，提出了一种基于近邻传播聚类分析的特征选择方法［7］。柯激情等在对高维蛋白质质谱数据进行处理分析时，结合稀疏表示理论提出了一种基于稀疏表示的特征选择算法［8］。游晓璐等针对蛋白质质谱特征提取问题，提出了一种基于多步降维和半监督学习的特征提取算法［9］。王跃锜等通过对非肌性肌球蛋白质谱进行分析研究，深入探讨了非肌性肌球蛋白重链9对食管癌的影响［10］。

不论是利用蛋白质波谱数据对何种问题进行研究，都会需要对大量的波谱数据进行分析。在这个过程中，如何降噪、选取特征一直是一个重要的研究课题。本论文中提出了一种基于高频系数的小波分析技术和主成份分析技术的特征提取方法，之后通过线性判别分析进行模式分类。

2 理论方法

2.1 小波及高频系数

小波作为一重要的线性时频展开方法，它在时域和频域里都能很好的表征局部信号特征，它是将信号展开为持续时间很短的高频基函数和持续时间较长的低频基函数。高频系数当中含有噪声，通常认为低频可以较好的表征信号特征。但是在文献［11］中，通过对信号进行小波分析，之后提取其高频系数作为特征，也取得了很好的分类效果。本文中将采用高频系数作为特征进行研究。假设L2 （R）是R上平方可积函数所构成的函数空间。若Ψ （t）∈L2（R），并且其傅里叶变换Ψ＾（ω）满足条件：称Ψ是一个基小波或者称作母小波，其中，R为实数，t为时间。把基小波伸缩和平移，可以得到一个小波序列x－b其中，a，b∈R，并且a≠0。a称为伸缩因子，b称为平移因子。式子

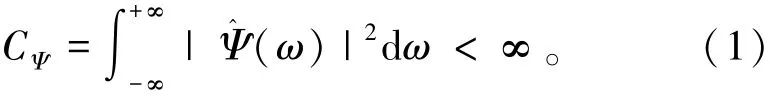
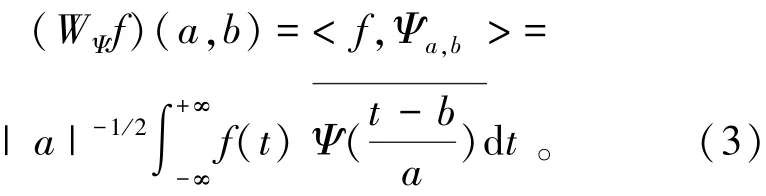
运算。在实际问题中，小波变换中的伸缩因子和平移因子往往都不是连续的，此时数值计算中需要采用离散小波变换。取a＝，b＝nbo，m，n∈Z代入式（2），得到相应的离散小波变换［12］：

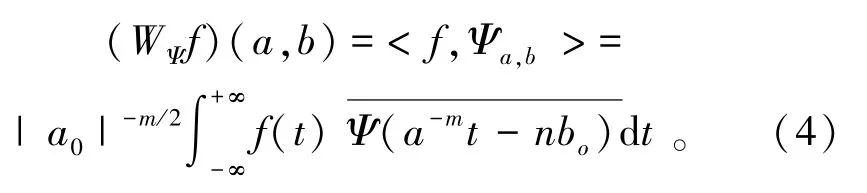
本文中，采用了离散小波变换，其中，Z为整数。

小波分析中，选择一个小波基并确定一个小波分解的层次N，然后对已知信号进行N层小波分解，如图1所示为小波分解高频系数提取示意图，图2、图3为小波处理提取高频系数前后的波形对比。

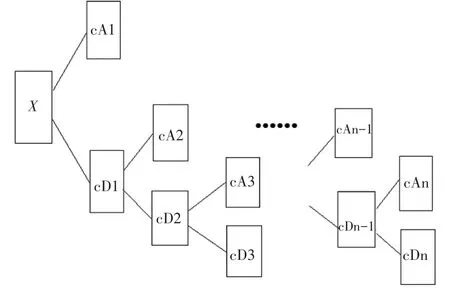
图1 小波分解及高频提取Fig.1 Wavelet decomposition and wavelet basis and high frequency extraction

图2 4－3－02数据集第一组数据原始信号波形Fig.2 The originalwaveform of the first series data of 8－7－02 data set

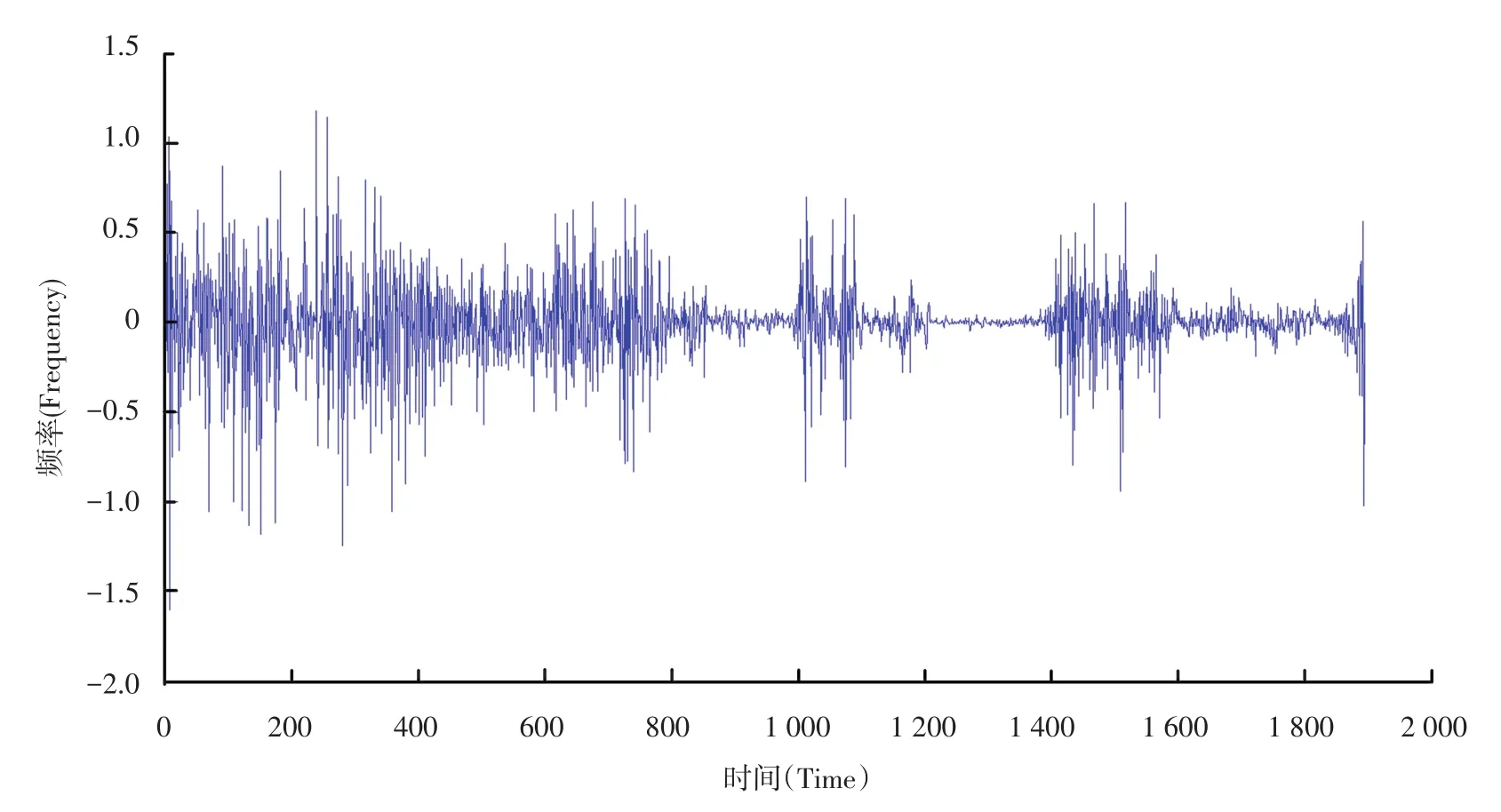
图3 4－3－02数据集第一组数据提取高频系数后波形Fig.3 Waveform after extractting the high frequency coefficients of the first series data of 4－3－02 data set

2.2 主成份分析

主成分分析（principal component analysis，PCA）是将多个线性相关变量压缩为少数几个不相关的变量的一种多元统计方法［13］。它通过提出严格线性相关或相关性较强的自变量的信息，选择其中某些维度来表征原有数据，以此达到降维的目的。通常，它对数据各维度进行信息贡献率的计算，并对数据维度按照贡献率排序。之后，可以根据需要自行选取特定的维度来表征原始数据。它在图像处理中的应用已是十分广泛，在蛋白质波谱数据处理中也有应用。假设问题中有p个指标，我们把这些指标看成p个随机变量X1，X2，…，Xp，主成分分析是要把这p个指标问题转化为p个指标的线性组合问题。这些新指标F1，F2，…，Fk（k≤p），遵循保留主要信息量原则来反映原来指标信息，并且它们相互之间独立。

F1＝u11X1＋u21X2＋...up1Xp

F2＝u12X1＋u22X2＋…up2Xp

……

Fp＝u1pX1＋u2pX2＋…uppXp

满足如下条件：

（1）每个主成分系数平方和是1，即

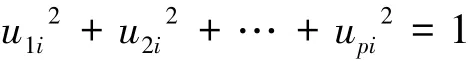
（2）主成分之间相互独立，即

Cov（Fi，Fj）＝0，i≠j，i、j＝1，2，…，p

（3）主成分的方差递减，重要性递减，即

Var（F1）≥Var（F2）≥…≥Var（Fp）

F1、F2…Fp分别称为原始变量的第一、第二、第p个主成分。

2.3 线性判别分析

线性判别分析（Linear Discriminant Analysis，LDA），通常也被称作Fisher线性判别（Fisher Linear Discriminant，FLD），它的基本的思想是把高维的样本数据信息投影到另一个更为适合的矢量空间中，从而抽取出适合于分类分析的数据信息以或者达到压缩特征空间维数的效果。

给定一个训练集 V＝（v1，v2，…，vm），V⊂Rn∗m，训练集中的样本，每个属性包含一个人脸图像的像素值，并且每个人脸图像属于一个类。Sw和Sb分别是类间散射矩阵和类内散射矩阵，它们分别定义如式（5）、式（6）：

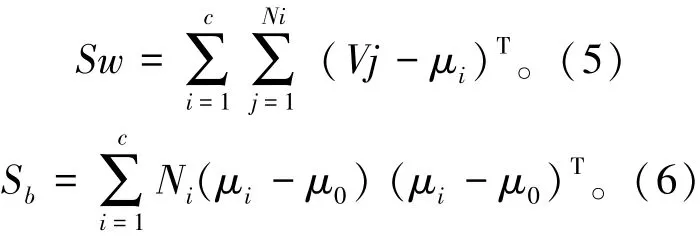
其中，Ni是训练集Vi中的样本数量。

LDA方法的目的是搜寻一个基础向量群，这个向量群中有不同类别的样本，而且拥有最大类间散射和最小类内散射。假定Sw是非奇异的，那么它的最佳投影矩阵就可以定义为式（7）所示：

其中，Wopt＝［W1W2...Wc－1］可以通过求解广义特征值问题来获得：

因为广义特征方程只有在c－1维空间中作为Sb矩阵存在，才能真正的得到优化，至少在c－1维空间中，Wopt＝［W1W2...Wc－1］是与c－1最大广义特征值相关的特征向量［14］。

当Sw是非奇异的时，其广义特征值可以表示为：

2.4 实验验证

在模式识别领域，对于机器学习问题，通常采用交叉验证的方法对实验效果进行评估。交叉验证是机器学习数据重抽样常用的方法，并且被广泛使用。交叉验证主要有三种，Handout验证、k折交叉验证（K⁃fold cross⁃validation）、留一验证（Leave⁃m⁃out）。本论文中主要使用 k折交叉验证（K⁃fold crossvalidation）。其思想可以简述如下：将样本集随机分为K个集合，通常分为K等份，对其中的K－1个集合进行训练，剩下的一个集合用来在分类器中进行样本测试。该过程重复K次，取K次过程中的测试错误的平均值作为推广误差。

3 实 验

3.1 实验数据

本论文中，总共对两组SELDI－TOF蛋白质质谱数据集对论文中方法的性能进行测试。两组数据集中有一组高分辨率卵巢癌数据集、一组低分辨率卵巢癌数据集。两组数据集来源于文献［15］。数据的命名也使用文献［15］中的命名方式。下面简单介绍这两组数据。

8－7－02数据集。这组低分辨率卵巢癌数据集在采集数据过程中使用了WCX2蛋白质芯片，然后使用升级的PBSII型SELDI⁃TOF质谱仪来生成质谱数据。这组数据集包含162个卵巢癌样本和91个正常样本。每个样本有15 154个特征。

4/3/02数据集这组数据也是低分辨率卵巢癌数据，亦是采用WCX2蛋白质芯片制备样本的。这组数据集由100个卵巢癌样本和100个正常样本组成。每个样本有15 154个特征。

3.2 实验思路

将数据预处理后，通过小波分析技术进行降维处理，提取高频系数，之后使用PCA技术，继续降维，取出主成分属性。然后用LDA作为分类器，通过k⁃fold交叉验证，分类数据，并评估其性能。主要过程如图4所示。

图4 实验流程图Fig.4 Experiment flow

SELDI-TOF-MS——蛋白质波谱数据

小波分析（高频系数）——数据降维

PCA分析——特征提取

LDA——分类识别

3.3 实 验

3.3.1 8－7－02数据集

对8－7－02数据集实验结果进行分析。实验过程中，首先，确定PCA分析所取最佳属性，实验中，取能表征数据集90％以上主成分分量的最佳属性。经测试，8－7－02数据集经过小波高频分析和主成分分析后，前15维属性贡献率之和达到90.22％，因此取其前15维属性，如图5所示。

图5 8－7－02数据集部分主要维度属性贡献率Fig.5 Contribution rates of somemain properties of 8－7－02 data set

通过图4的思路，对8－7－02数据集进行分类，其中k⁃fold验证中参数取5，小波变换过程中，分解层数分别取1到5层，小波基分别取haar和dbN小波系，提取高频系数。最终得到在不同小波分解层数和不同小波基条件下的分类情况。实验结果如表1所示：

由实验结果数据可以看到，随着小波分解层数增加，分类正确率、灵敏性、特异性都略有下降，每增加一层分解，数据属性维度就会减少一半，数据维度太多或太少，都不能很好的实现分类效果。另外，小波分解之后，对得到数据进行主成分分析，数据的前少数属性维即可很好的表征数据特征，不需要太多冗余属性维，这大大降低了数据维度，为之后的分类减轻了很大的负担，极大的提高了效率。同时，实验还说明了对数据进行小波分析后的高频数据，对于模式分类也是很有利的。最终经实验分析得出，8－7－02数据集在使用haar小波基，小波分解层数为3，取前15维属性时，实验的分类效果最佳：正确率100％，灵敏性96.35％，特异性98.52％（见表1、表2、表3）。

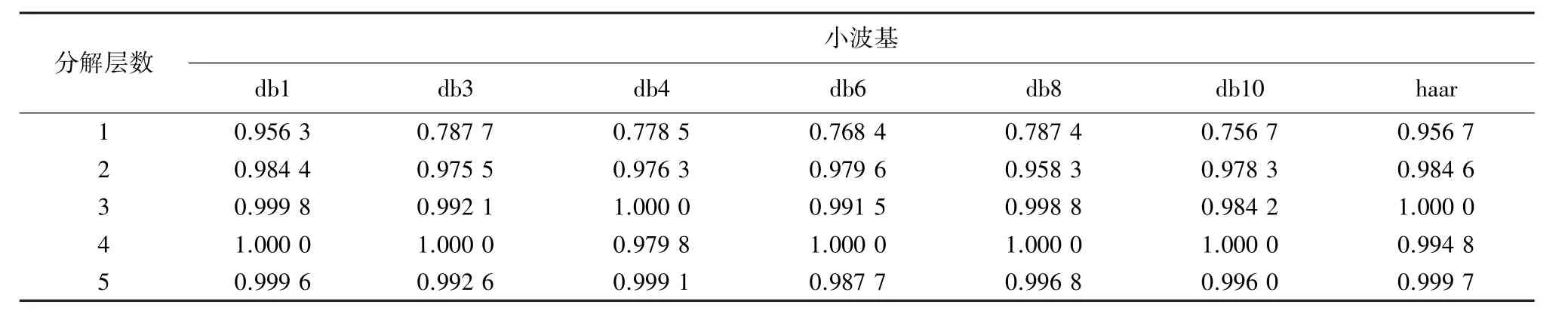
表1 不同小波基在不同分解层数条件下分类正确率Table 1 Accuracy of classification under the different conditions of wavelet basis and levels

表2 不同小波基在不同分解层数条件下对应灵敏性Table 2 Sensitivity under the different conditions of wavelet basis and levels

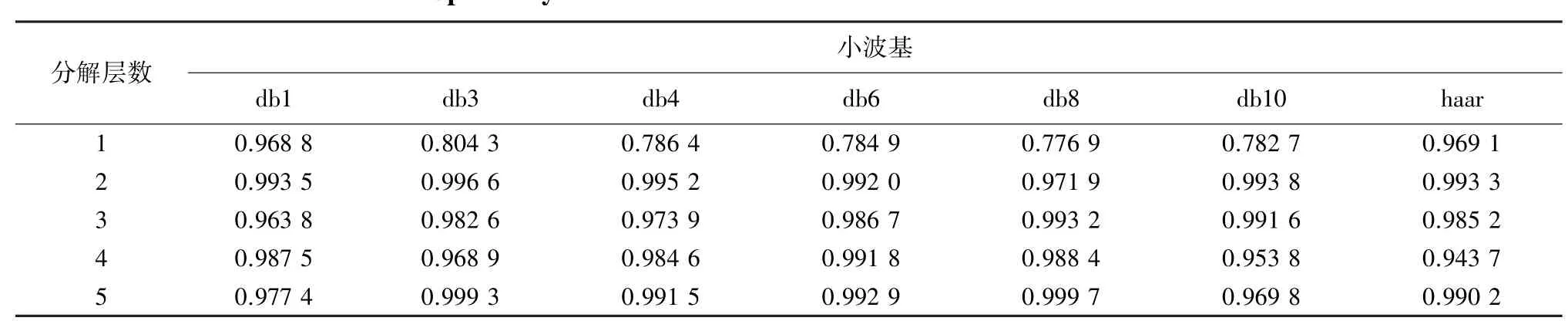
表3 不同小波基在不同分解层数条件下对应特异性Table 3 Specificity under the different conditions of wavelet basis and levels

下面，对比选取不同主成分属性实验效果，实验中固定小波基和分解层数，分别取前6、8、10维属性，使用db3小波基、3层分解时，实验结果对比如表4所示：

由表4中数据，我们可以看到，随着维度数量的增加，正确率逐渐提高。

3.3.2 4/3/02数据集

经实验处理后，本组数据前84维属性贡献率之和达到90.10％，因此实验中取前84维如图6：

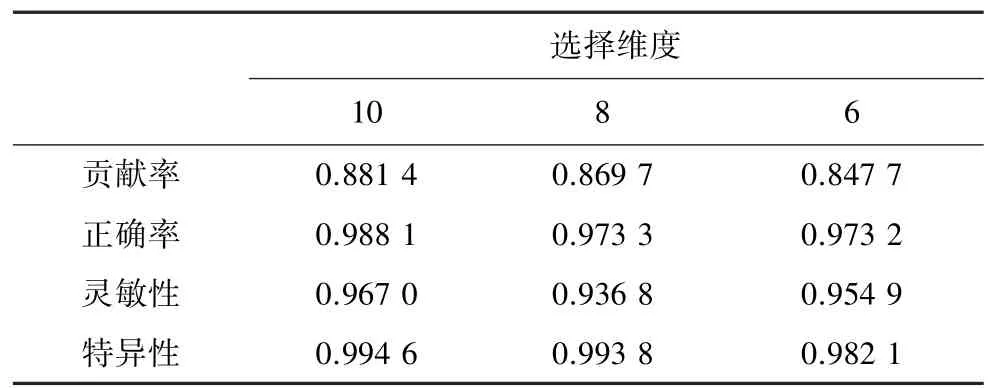
表4 不同维度数据在相同小波分解条件下结果Table 4 Classific result under the conditions of different dimensions and same wavelet basis

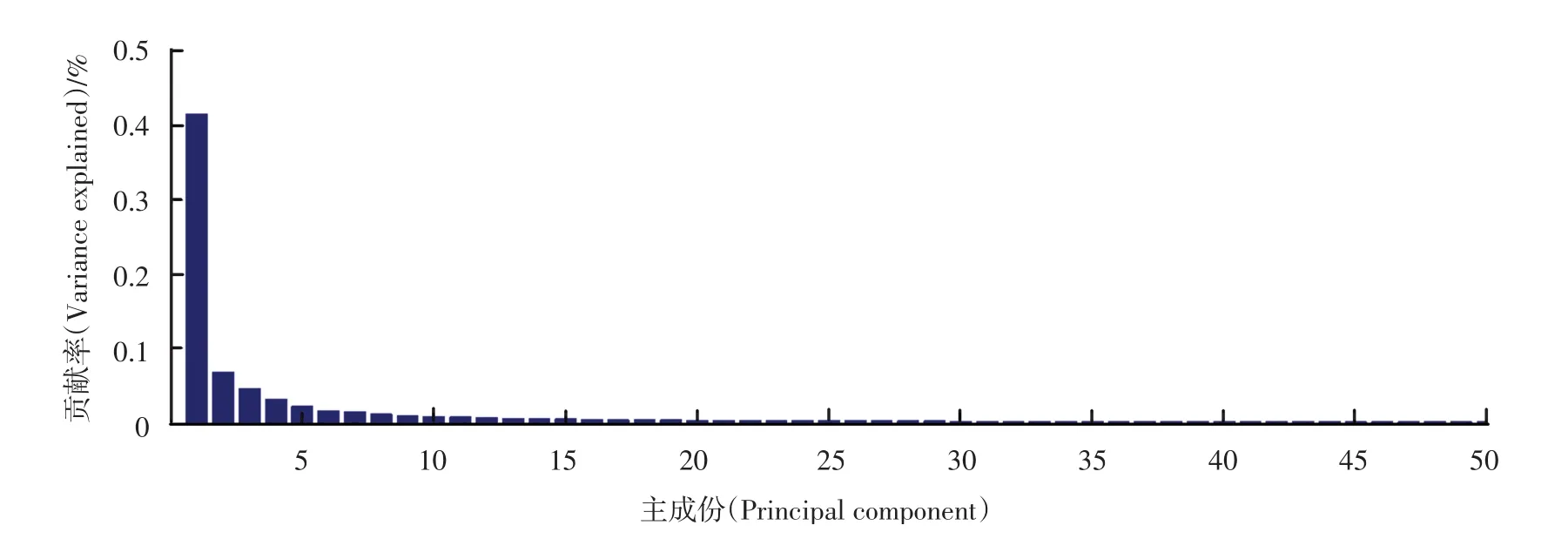
图6 4/3/02数据集部分主要维度属性贡献率Fig.6 Contribution rates of somemain properties of 4/3/02 data set

由实验数据我们看到，对4/3/02数据集进行实验，当使用haar小波基，小波分解层数为4时，其分类效果最佳：正确率99.45％，灵敏性99.65％，特异性99.25％（见表5、表6、表7）。

表6 不同小波基在不同分解层数条件下对应灵敏性（4/3/02数据集）Table 6 Sensitivity under the different conditions of wavelet basis and levels（4/3/02 data set）

表7 不同小波基在不同分解层数条件下对应特异性（4/3/02数据集）Table 7 Specificity under the different conditions ofwavelet basis and levels（4/3/02 data set）

4 讨论与结论

在本论文中，我们使用小波分析后的高频系数经过一系列的实验后发现，同一组数据，在进行小波分解时，采用同一小波基，当分解层数不同时，分类结果会稍有不同，比如8－7－02数据集在使用db3小波基时，在一到五层分解时正确率分别为78.77％、97.55％、99.21％、1、99.26％。此外，不同小波基，在相同分解层数条件下，对于数据分类结果，也会有不同影响，正确率会有所不同，但是差别不大，如8－7－02数据集在进行3层小波分解时，分别使用db1、db3、db4、db6、db8、db10、haar小波基时正确率分别为99.98％、99.21％、100％、99.15％、99.88％、98.42％、100％。高于文献［11］的综合识别率。同时也进一步说明，小波分析过程中的高频系数也可以很好的表征数据特征。

本文提出的模型中，先对蛋白质波谱数据进行各种不同的小波分解并提取高频信息，然后通过主成分分析提取特征，之后将特征送入LDA分类。经实验，本方法可以有效的降低数据计算量，提高效率，并取得了较好的分类效果。

［1］ LIU Yihui.Feature extraction and dimensionality reduc⁃tion formass spectrometry data［J］.Computers in Biology and Medicine，2009，39：818－823.

［2］ BEHDAD M，FRENCH T，BARONE L，etal.On princi⁃pal component analysis for high⁃dimensional XCSR［J］. Evolutionary Intelligence，2012，5（2）：129－138.

［3］ 李义峰，刘毅慧.基于遗传算法的蛋白质质谱数据特征选择［J］.计算机工程，2009，35（19）：192－197. LIYifeng，LIU Yihui.Feature selection for protein mass spectrometry data based on genetic algorithm［J］. Computer Engineering，2009，35（19）：192－197.

［4］ BALDIP，LONG A.A Bayesian framework for the analysis of microarray expression data：regularized t⁃test and statistical inferences of gene changes［J］. Bionformatics，2001，17：509－519.

［5］ ZHAO J.Asymptotic convergence of dimension reduction based boosting in classification［J］.Journal of Statistical Planning and Inference，2013，143（4）：651－662.

［6］ 李义峰，刘毅慧.基于模拟退火算法的高分辨率蛋白质质谱数据特征选择［J］.生物信息学，2009，7（2）：85－90. LI Yifeng， LIU Yihui.Feature selection based on simulated annealing algorithm for high⁃resolutio protein mass spectrometry data［J］. Chinese Journal of Bioinformatics，2009，7（2）：85－90.

［7］ 杨合龙，祝磊，韩斌.运用近邻传播聚类分析进行SELDI⁃TOF蛋白质谱特征选择［J］.中国生物医学工程学报，2013，32（1）：14－18. YANG Helong，ZHU Lei，HAN Bin.SELDI⁃TOF protein mass spectrometry feature selection based on neighbor clustering analysis［J］.Chinese Journal of Biomedical Engineering，2013，32（1）：14－18.

［8］ 柯激情，祝磊，厉力华，等.基于稀疏表示算法的蛋白质质谱数据特征选择［J］.生物物理学报，2012，28 （8）：683－691. KE Jiqing，ZHU Lei，LI Lihua，et al.Feature selection of protein mass spectrometry data based on sparse representation algorithm ［J］. Acta Biochimica et Biophysica Sinica，2012，28（8）：683－691.

［9］ 游晓璐，祝磊，曹凯敏，等.基于多步降维和半监督学习的蛋白质质谱特征提取算法［J］.航天医学与医学工程，2013，26（4）：312－316. YOU Xiaolu，ZHU Lei，CAO Kaimin，et al.Feature selection of protein mass spectrometry data based on Multi⁃step dimensionality reduction and semi⁃supervised learning［J］.Space Medicine＆Medical Engineering，2013，26（4）：312－316.

［10］王跃锜，张旭，何海蓉，等.食管癌细胞线粒体中MYH9蛋白的分布及与SLP－2结合的研究［J］.肿瘤防治研究，2015，42（3）：229－232. WANG Yueqi，ZHANG Xu，HE Hairong，et al.The distribution of MYH9 in esophageal cancer cells mitochondrial protein and research combined with SLP－2 ［J］.Cancer Research on Prevention，2015，42（3）：229－232.

［11］刘玉杰，刘毅慧.基于小波高频系数基因芯片数据的特征提取［J］.生物信息学，2011，9（4）：339－343. LIU Yujie，LIU Yihui.Feature extraction of gene chip data based on wavelet high⁃frequency coefficients［J］. Chinese Journal of Bioinformatics， 2011， 9（4）：339－343.

［12］张德丰.MATLAB小波分析（第二版）［M］.北京：机械工业出版社，2011. ZHANG Defeng.The Wavelet Analysis of Matlab（The second edition）［M］.Beijing：China Machine Press，2011.

［13］GELADIP.Notes on the history and nature of partial least squares（PLS）modeling［J］.Journal of Chemometrics，1988，2：231－246.

［14］ZHOU Changjun，WANG Lan，ZHANG Qiang，et al. Face recognition based on PCA image reconstruction and LDA［J］.Optik，2013，124：2299－5603.

［15］李义峰.基于优化算法的蛋白质质谱数据分析［D］.济南：山东轻工业学院，2009. LI Yifeng.Optimization Algorithms Based Protein Mass Spectrometry Data Analysis［D］.Jinan： Shandong Polytechnic University，2009.

Feature selection forhigh⁃dimensional protein mass spectrometry data based on the high frequency coefficients of wavelet analysis

WUWenfeng，LIU Yihui∗
（School of Information，Qilu University of Technology，Jinan 250353，China）

During the analysis of high⁃dimensional protein mass spectrometry data，feature selection of the data is always the focus for many researchers.In this paper，we proposed a feature selection method based on the high frequency coefficients ofwavelet analysis and principal component analysis.Firstwe used wavelet analysis to reduct the noise，and extracted the high frequency coefficients as the feature.Then we use PCA to reduce the dimensions. The test show thatwhen themethod was applied to the data set 8－7－02，4/3/02，we can get different recognition rates of 100％and 99.45％，respectively，indicate themethod can improve recognition rates effectively.

Spectrometry data；High frequency coefficients；Wavelet analysis；Principal component analysis

Q629.73

A

1672－5565（2015）03－198－07

2015－04－20；

2015－05－08.

吴文峰，男，硕士研究生，研究方向：智能信息及图像处理；E⁃mail：641178636＠qq.com.

∗

刘毅慧，女，博士，教授，研究方向：生物计算，智能信息处理等；E⁃mail：yxl＠sdili.edu.cn.