目标搜索中的步长改变比率临界值仿真研究

张国超，王俭

（1.苏州中软国际科技服务有限公司，江苏苏州215123；2.苏州科技学院电子与信息工程学院，江苏苏州215009）

目标搜索中的步长改变比率临界值仿真研究

张国超1，王俭2

（1.苏州中软国际科技服务有限公司，江苏苏州215123；2.苏州科技学院电子与信息工程学院，江苏苏州215009）

针对变步长目标搜索任务中的步长改变比率的确定问题，采用计算机仿真手段，在均匀和非均匀两种土质对应的气味源扩散及气味浓度场分布情况下，验证了机器人六边形变步长目标搜索问题中初始步长改变比率满足的一个约束不等式，进而找到一个新的更准确的联立不等式约束关系，最后给出一个可计算的修正公式。

目标；搜索；跟踪；信号强度；步长；临界值

探测目标发出信号的强度并根据测量值进行目标搜索、跟踪以及定位有着越来越广泛的应用[1-4]。现以机器人对土壤中气味源的搜索为例，通过计算机仿真，研究搜索过程中步长改变比率的取值。步长改变比率指后一步与前一步两者长度之比，比率大于1，意味步长增加；比率小于1，意味步长较小，比率等于1，意味步长不变。

Russell最早提出移动机器人携带传感器并测量自身当前位置下土壤表层中的气味浓度，进而跟随气味浓度增大的方向寻找地下气味源的定步长六边形搜索策略[1]，其主要特点之一就是机器人自点n-1来到点n后，将根据过往测得的气味浓度，向左或者向右转60°，继而行走一步的距离，前往点n+1或点n+1’（图1a）。

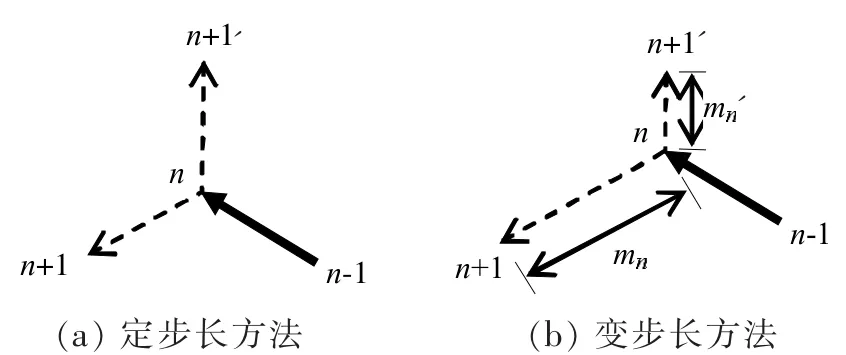
图1 六边形搜索策略示意

文献[3]对定步长六边形搜索策略进行了改进，提出途中阶段和结束阶段变步长的搜索策略（图1b），给出了具体的途中步长改变比率的计算方法和公式，即机器人根据当前（点n）的气味浓度测量值和过去（点n-1及以往诸点），决定下一步行进的方向（点n+1或点n+1'）和步长（mn或mn'），改进了搜索效果。

至于步长改变比率取值的范围，或者说步长改变比率的临界值，文献[3]通过推导给出了两个不等式约束。但是，受限于参数值无法确定和预知，在实际的搜索中无法实时地精确计算两个不等式的值，因而两式都没有在变步长策略中得到实际应用。所以，从理论上讲机器人可能由于实际的步长衰减过快而中途停止，即收敛速度过快导致

的问题仍没有彻底解决。式（1）中，d（s）表示机器人与目标的欧氏距离，dth为目标邻域的半径，s为步数。图2清楚地表达了步长改变比率过小而极易导致机器人在搜索途中停止的潜在可能性。

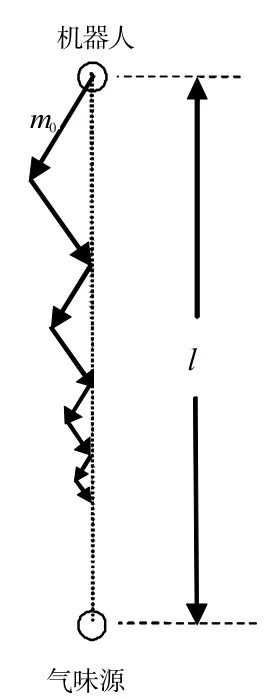
图2 步长逐步减小

文中将通过计算机仿真验证一个约束关系，并根据仿真对其进行修正，从而对搜索起始步长和初始步长改变比率的取值有更明确的范围，为优化搜索策略及算法做准备。

1 不等式约束的分析

文献[3]给出的步长改变比率k的临界约束的两个不等式，一个通过即时的位置和信号源强度表达

其中，N(·)为即时信号强度，N0为目标信号强度，x为机器人或者说是测量点与目标的距离。另一个通过初始距离和初始步长表达（见图2）。

其中，m0是初始步长，l是起点至气味源的距离。不难看出，式（2）适用于确定搜索途中实时的步长改变比率，而式（3）适用于确定搜索开始阶段的初始步长改变比率。

特别地，式（3）的物理意义非常明确，就是如果初始距离越远，初始步长可以越大，同时意味着初始步长改变比率可以越小。而且显然，如果假设起点至气味源的初始距离已知，那么尝试不同的初始步长，则式（3）是可以验证的。对于式（2），由于其验证研究需要更多的准备工作，故将留待今后适当时机。

2 仿真工作

气体分子在均匀土质中的扩散是各向一致的，形成的气味场是均匀的，等强度线是同心圆。而非均匀土质中的气味场分布则要复杂得多[5]（见图3）。

在均匀土质和非均匀土质两种环境进行仿真，统计得出在每种环境下，不同起始点和不同初始步长情况下，步长改变比率的临界值，最终要证实一般非均匀土质中机器人任意起点、任意方向开始的变步长搜索行为，其步长改变比率确实由式（3）所约束。

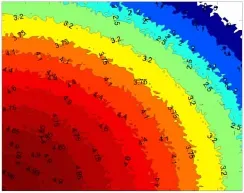
图3 非均匀土质中的气味场分布示意

2.1 仿真方案的设计

搜索策略：从任意起点开始。每当途中每两步之间的停留点，在左前方60°方向一个探测臂长度处和右前方60°方向一个探测臂长度处，各测量得到一个浓度值，然后朝浓度值较大的那个方向行进一步。如此重复，直至与目标距离小于预设的目标邻域半径时停止搜索。

仿真方案：随机给定起点坐标、初始步长、邻域半径（取等于初始步长值），给定步长改变比率。开始搜索，同时绘制机器人搜索的轨迹，并统计每次搜索过程的步数、路程、最终与目标的距离等等数据。在不同步长改变比率下，多次重复。

数据记录：需要统计记录的仿真数据包括“初始距离”、“初始步长”、“预设邻域半径”、“理论临界值”、“步长变比”、“步数”、“最终记录”。

分析项目：根据式（3）计算出在气味分布场中的步长改变比率临界值。根据仿真数据计算得到不同步长改变比率对应的“步数增幅”，并比较记录的各次“步数”、“路程”和“最终距离”。

仿真步骤：任意选定起始点即任意给定初始距离，设定初始步长，完成搜索并记录相关数据；改变初始距离，初始步长，完成搜索并记录相关数据；重复以上步骤（见图4）。

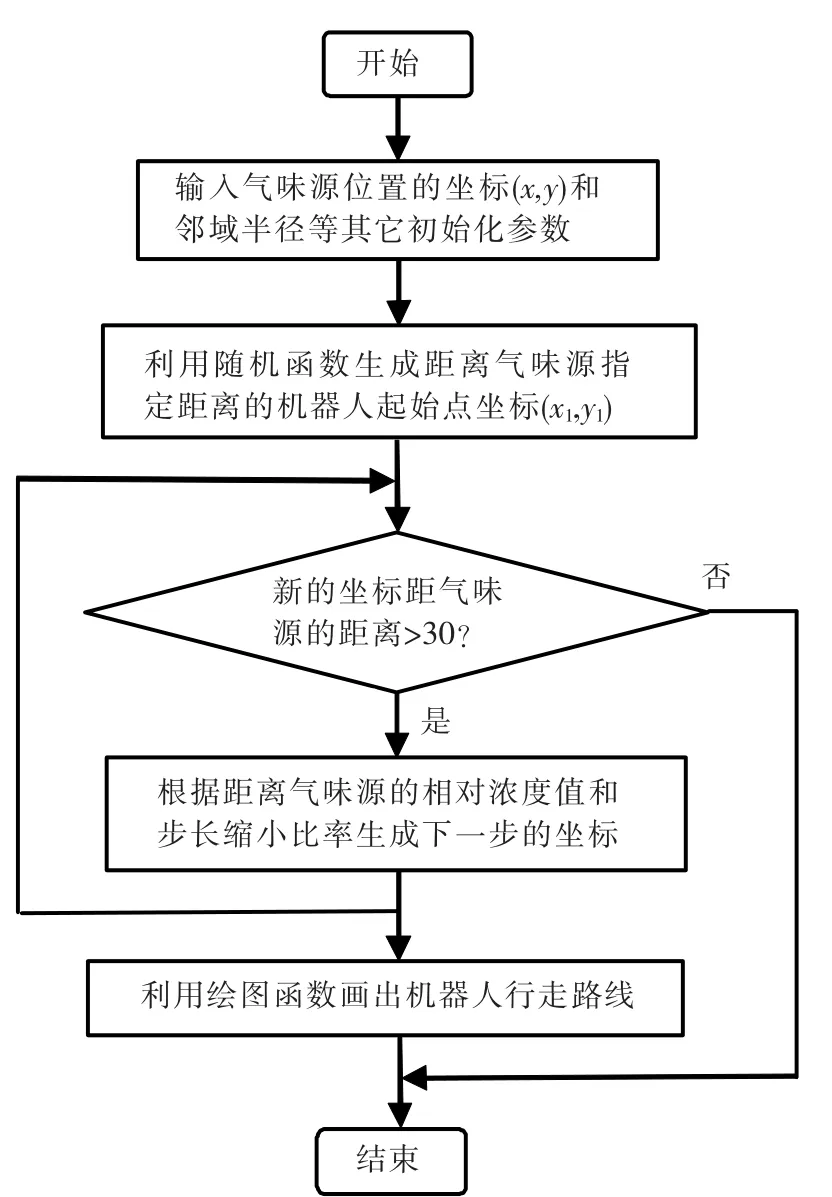
图4 仿真流程图

2.2 搜索的路径及其特征

满足式（3）的步长改变比率可以保证机器人无限接近目标，即进入邻域以内（图5a），而不满足式（3）的步长改变比率使机器人最终止步于邻域之外（图5b）。仿真证实，一般情况——非均匀土质任意起点任意方向下的搜索均存在这一现象。图6是在同一个给定的邻域半径下，步长改变比率大于某一数值时机器人与目标距离可以足够接近，和步长改变比率小于某一数值时机器人与目标距离无法进入邻域以内。

图5 均匀土质不同步长改变比率的两个搜索路径

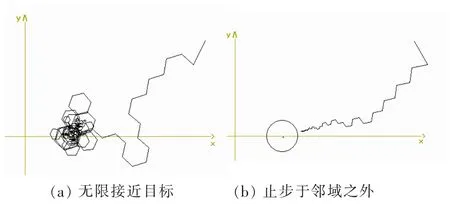
图6 非均匀土质不同步长改变比率的两个搜索路径

3 数据分析

3.1 仿真过程与数据

3.1.1 均匀土质仿真表1是一个仿真例数据，图7是其中两个关键数据“步数”和“最终距离”随“步长变比”的变化曲线。在该例中，初始距离取371.07个单位长度，初始步长和邻域半径均为30个单位长度。

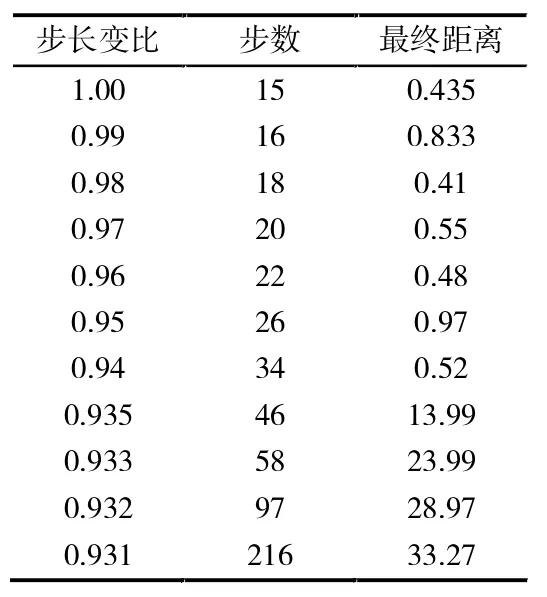
表1 均匀土质仿真例的关键数据

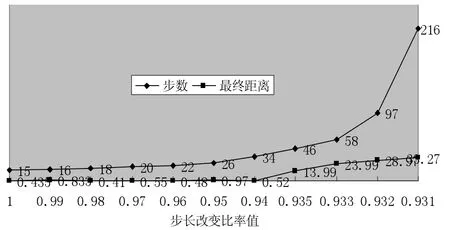
图7 均匀土质中步长改变比率对应的搜索步数和最终距离

3.1.2 非均匀土质仿真表2是一个仿真例数据，图8是该例中“步数”和“最终距离”随“步长变比”的变化曲线。

表2 非均匀土质仿真例关键数据

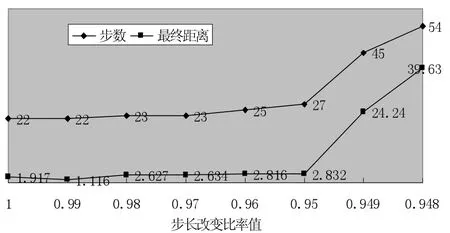
图8 非均匀土质中步长改变比率对应的搜索步数和最终距离

3.2 仿真数据分析

在文中全部仿真中，目标气味源的源浓度取5，起始点在距离目标476.34范围内任意选取，初始步长在30～50之间任意选取，浓度偏差在2.180 715以内任意选取，所有仿真结果呈现完全一致的规律，所以文中仅对上节所举均匀和非均匀土质气味源扩散的两例仿真结果及数据进行分析。

3.2.1 均匀土质仿真例分析从表1和图7看，当“步长变比”减至0.931时，“最终距离”——搜索的最终停止地点离目标的距离——就大于邻域半径了。同时，“步数”也从97跃增到216。也就是说，行进了极大的步数值也无法足够接近目标。结论是：实际的步长变比值必须大于0.931。

考虑到邻域半径的选取具有人为因素，因此再观察“最终距离”从0.52激增至13.99所对应的“步长变比”值，可看出，邻域半径取1个单位长度是一个足够小的值，可以认为选取邻域半径为1就是消除了人为因素。于是得结论：实际的步长变比值必须大于0.935。

3.2.2 非均匀土质仿真例分析从表2和图8看，当“步长变比”从0.949减至0.948时，“最终距离”相应地从24.24增加为39.63，即大于邻域半径。但是，仅凭借是否停止于邻域以内（或以外）作为判断步长变比临界值的理由，显然是不够有力的。且不说邻域半径的选取是人为因素，刚刚跑进邻域就停止和止步于邻域外咫尺之遥，其实并没有根本差异。即0.948作为临界值的理由不充分。

同时注意到，当“步长变比”从0.95减至0.949时，“步数”和“最终距离”两者有一个同步的较大幅度跃增，尤其是“最终距离”从一直小于3跃增到24.24。换言之，此例中邻域半径选取为3是合理的。结论是：实际的步长变比值必须大于0.949。

4 新的约束关系

前述分析表明，无论均匀或非均匀土质中，普遍存在一个关于几个临界值大小关系的联立不等式如下

其中，ksub是依据“最终距离”数据是否大于人为选取邻域半径得出的临界值，kobj是依据“最终距离”数据是否出现显著永久性跃增得出的临界值。kobj根据实际数据的客观规律，不受人为主观因素影响。

在表1和图7对应的均匀土质仿真例中，k为0.929，ksub为0.931，kobj为0.935，满足式（4）。在表2和图8对应的非均匀土质仿真例中，k为0.941，ksub为0.948，kobj为0.949，也满足式（4）。

合理的解释是：仿真获得的搜索路径不可能是径直走向目标的，会有一定的曲折即通俗所说的弯路，且越是实际浓度分布场则弯路越明显，所需步数比理论假设径直走向目标路径的步数要多，步长自然要经过更多次的缩短，将会更快地趋于零，更容易导致搜索中途停止。换言之，要保证搜索不会停止在中途，必须取更大的步长变比值。可以说，式（4）是比式（3）更准确的约束不等式。

但是，式（4）存在不便于计算的缺陷。实用上要想预先通过计算得到实际浓度场分布下的步长变比临界值，仍然是对式（3）进行修正，见式（5）。

在文中所设条件下及相应的全部仿真数据，修正系数ρ取1.1是保险的。

5 结语

文中通过计算机仿真，证实了在均匀和非均匀两种土质对应的气味源扩散及气味浓度场分布情况下，机器人六边形变步长目标搜索问题中初始步长改变比率满足的一个约束不等式的基本正确性，并根据仿真结果对该不等式进行了拓展，得到新的联立不等式约束，最后根据仿真数据，给出了实用的临界值修正公式。

这个结果与目标距离预估的结果相结合，将会对搜索初始阶段的初始步长选择和步长变比选择有指导作用，为搜索的优化起到帮助。该文后续工作将包括：参考有关研究者的成果[4，6]，对目标距离进行预估；寻找具有普适性的修正系数取值；对式（2）刻画的临界值不等式约束进行研究。

参考文献：

[1]Russell R A.Robotic location of underground chemical sources[J].Robotic，2004，22（1）：109-115.

[2]孟庆浩，李飞.主动嗅觉研究现状[J].机器人，2006，28（1）：89-96.

[3]王俭，季剑岚，陈卫东.基于行为特征的机器人变步长气味源搜索算法[J].系统仿真学报，2009，21（17）：5427-5430，5435.

[4]孟庆浩，李飞，张明路，等.湍流烟羽环境下多机器人主动嗅觉实现方法研究[J].自动化学报，2008，34（10）：1281-1290.

[5]葛卫龙，华良洪，张晓辉，等.等步长目标搜索算法中步长对搜索结果的影响[J].海军工程大学学报，2014，26（2）：25-28.

[6]谢彦春，潘欣裕，王俭.基于场分布探测值多边形匹配的搜索策略[J].计算机科学，2015，42（6A）：112-114.

Simulation of critical ratio of variant step-size in source searching

ZHANG Guochao1，WANG Jian2
（1.ChinaSoft International Technology Services Ltd.,Suzhou 215123,China;2.School of Electronic and Information Engineering,SUST,Suzhou 215009,China）

Aiming at how to determine the variant ratio of step-size in hexagon strategy for source searching,the computer simulation was used to firstly verify an inequality which constraints the initial value of the ratio of stepsize under a diffusing of odor-source in the uniform soil or non-uniform soil and the distribution of odor-concentration field,secondly a new more accurate simultaneous inequality was found,finally a calculable correction formula was given.

target;searching;tracing;signal strength;step-size;critical value

TP242.6

A

1672-0679（2015）04-0076-05

（责任编辑：卢文君）

2015-07-26

国家自然科学基金项目（61372146）；江苏省高等教育教学改革研究基金（2013JSJG063）

张国超（1992-），男，江苏丹阳人，工程师。

王俭（1956-），男，教授，硕士，从事智能体与智能信息处理的研究，Email:wangjiansuzhou@sina.com。