自由曲面形状和拓扑联合优化研究

马 腾，赵兴忠，2，高博青，吴 慧

（1.浙江大学空间结构研究中心，浙江杭州310058；2.中国中元国际工程有限公司，北京100089；3.浙江财经大学城乡规划与管理学院，浙江杭州310018）

自由曲面形状和拓扑联合优化研究

马 腾1，赵兴忠1，2，高博青1，吴 慧3

（1.浙江大学空间结构研究中心，浙江杭州310058；2.中国中元国际工程有限公司，北京100089；3.浙江财经大学城乡规划与管理学院，浙江杭州310018）

为了得到形状与拓扑这两大因素共同影响下的自由曲面形状和拓扑的最优解，以结构鲁棒性为优化目标，将自由曲面的形状和拓扑同时作为优化的变量，采用差分演化算法进行优化求解，实现了全局最优的曲面形状和网格拓扑.算例表明，与形状和拓扑优二者分开优化相比，优化得到的该结构鲁棒性更高，结构力学性能更优，求得的曲面形状和网格拓扑能够有效地抵抗所对应的荷载，体现结构的主要传力路径.

自由曲面结构；形状和拓扑；鲁棒性；联合优化

对于自由曲面结构，影响其力学性能的有2个主要因素，分别是曲面的形状和拓扑.初始的建筑设计方案，在带来视觉冲击的同时，往往难以兼顾结构的受力性能.为了达到建筑形态与力学性能的协调一致，众多学者从优化角度，探讨曲面的合理形状、杆件的合理拓扑.

在自由曲面结构的合理形状创建方面，崔昌禹等[1]通过杆件节点坐标的移动，逐步减少结构应变能，获得受力性能良好的自由曲面网壳结构形式；武岳等[2]提出曲线变换型自由曲面的形态创建方法，通过母线沿准线平移、缩放、旋转，创建复杂的网格形式，由于曲线的B样条控制点相较曲面的离散点数量大幅降低，提高了优化效率；Espath等[3]研究以NURBS的控制点坐标、权因子、节点矢量为优化变量的曲面优化方法；李娜等[4]根据仿生原理，进行仿扇贝形体的网壳结构创建，并进行形态优化.以上研究均以NURBS曲面形状构建作为理论基础，已成为找形技术研究和工程应用领域的主流方法[5].

自由曲面结构的合理拓扑布置是工程设计中的一大难点，一些工程实例的网格生成仍依赖人工操作和经验，如阳光谷工程的网格划分[6].为了找到结构的合理拓扑，Rasmussen等[7]通过定义节点与节点之间是否有杆件连接的方法，探讨了析架拓扑优化的离散型方法；连续体拓扑优化[8]是寻找结构的力学传导路径的优化方法，经典的方法如均匀化方法、进化结构法、变密度法（SIMP）等，均适用于曲面结构的拓扑优化设计；SIMP方法[9]是目前广泛应用的连续体拓扑优化方法，它将一般变密度法的0-1离散问题松弛为[0，l]之间的连续优化问题，降低了求解难度.

自由曲面结构同时受到形状与拓扑这2类变量的影响，而目前的研究多将两者分开进行.寻找最优的结构形态，应同时将形状和拓扑变量作为优化变量进行优化，但目前研究者甚少.Wang等[10]运用差分调整NURBS曲面高度进行形状优化，然后在最优形状上运用OC法进行拓扑优化，因此该方法是在最优形状基础上的拓扑优化，没有考虑形状和拓扑变量的藕合性.Ansola等[11]进行自由曲面形状与拓扑综合优化研究探索，在迭代中，先进行一次微小的Coons曲面形状优化；然后在优化形状的基础上，进行一步微小的拓扑优化，每一次优化均是在前一步优化的基础上进行，如此反复循环，虽然算法能够收敛，但是否达到全局最优有待检验.

本文采用H∞结构鲁棒性评价指标[12-13]，该指标能够较好地反映曲面的形状和拓扑合理性.以该指标为优化目标，取NURBS控制点坐标作为形状控制变量，取SIMP相对密度作为拓扑优化变量，运用DE算法求解自由曲面的形状和拓扑联合优化问题.算例表明，DE算法能够适应不同变量同时存在下的优化问题，采用联合优化设计的自由曲面网壳，相比依次进行形状优化和拓扑优化，力学性能更加优越.

1 自由曲面形状拓扑联合优化原理

1.1 NURBS曲面创建原理及SIMP连续体拓扑优化

NURBS是目前自由曲面创建的主流方法，NURBS参数化的特点十分适用于曲面的创建与修改，曲面创建过程高效稳定，具体可以参见文献[14].

离散型拓扑优化本质是一种0-1离散变量的组合优化问题，0代表材料无，1代表材料保留.直接求解0-1优化模型有诸多不便，而采用SIMP模型的思想，将材料有无变化变为均匀性变化，成为连续优化问题.

SIMP拓扑优化[15]将单元的相对密度ρ作为设计变量，以连续变量的密度函数形式显式地表达单元相对密度与材料弹性模量之间的对应关系.引入惩罚因子对中间密度进行惩罚，使中间密度向0/1两端聚集，连续变量的拓扑优化模型逼近0-1离散变量的优化模型.对该模型进行有限元求解时，中间变量对应一个很小的弹性模量，对刚度矩阵的影响变得很小.SIMP采用的弹性模量与相对密度的插值关系如下：

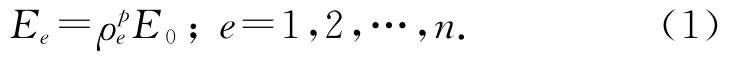
式中：Ee为第e个单元的插值弹性模量，E0为实际材料的弹性模量；0＜ρe≤1为材料相对密度；p为惩罚参数，一般取p≥3，本文取3；n为单元数目.1.2 联合优化数学模型

进行自由曲面形状拓扑联合优化的数学模型如下.

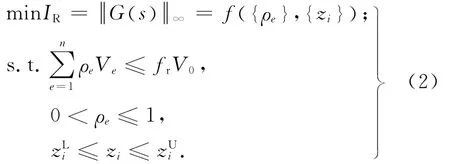
优化目标是使结构鲁棒性指标IR最小.设计变量ρ=[ρ1，ρ2，…ρn]为单元的材料相对密度向量，Z= [z1，z2，…，zm]为NURBS曲面控制点坐标向量，fr为允许保留的材料体积比，Ve和V0分别为第e个单元的体积和总体积限值.

式（2）的优化目标IR为基于H∞鲁棒控制理论建立的结构鲁棒性评价指标.将结构视为一个输入输出系统，则结构系统传递函数的H∞范数即IR.IR可以衡量结构系统输出信号与输入信号是否相称，反映结构对各种干扰的敏感性，体现结构的健壮程度，即鲁棒性，关于H∞结构鲁棒性理论的详细研究参考文献[16]的研究.

式（2）的求解采用差分演化算法（differential evolution）[17].该方法是一种有效的全局最优解的搜索算法.对于式（2）的不等式约束，本文采用引入惩罚函数逐步逼近方法.

对于自由曲面结构，本文采用SIMP法得出以相对刚度为连续变量的拓扑优化模型，并按式（2）的优化目标，采用DE算法搜索得到最优解.

2 算例分析

2.1 联合优化与单独形状、拓扑优化对比

通过对比联合优化结果与传统的单独形状、拓扑优化结果，验证联合优化的合理性.

本例的结构模型为如图1所示的一单位正方形平面，施加均布荷载q=11k N/m2，求解结构上凸时的最优形状和拓扑.曲面控制点分布、网格数量20×20分别如图2、3所示，fr=0.5.基于结构对称性，控制点取2、3、6、7、8、11、12、13共8个，其余控制坐标由对称取得，在1/4结构单元中引入SIMP变密度，剩余单元SIMP变密度由对称取得.

图1 单位正方形结构模型Fig.1 Unit square structure model

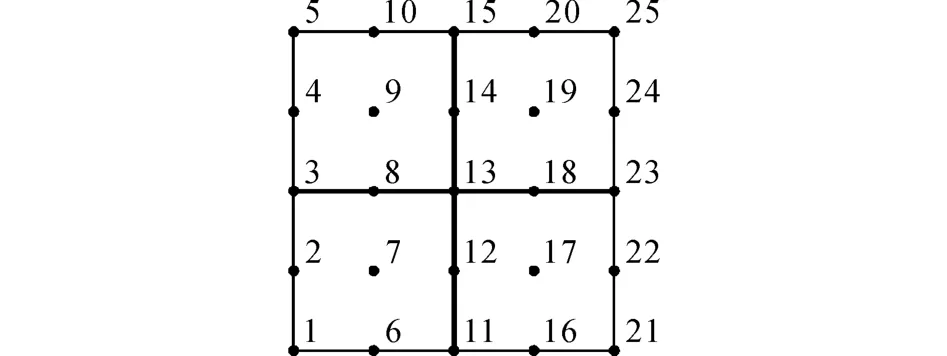
图2 曲面控制点分布Fig.2 Distribution of curve control points

图3 有限元网格划分Fig.3 Meshing of finite element

本例共进行两类结构优化：1）单独形状、拓扑优化，即先对结构进行单独的形状优化，取所有的单元相对密度ρi=1，在此优化基础上进行单独的拓扑优化，如图4所示为最终的优化结果；2）本文提出的形状和拓扑的联合优化，两类变量同时进行优化求解，约束条件同第一类.优化结果如图5所示.

优化结果的形状对比：以0.3 m等高线作为对比，采用单独优化的曲面中部突起范围更广、更加平坦；两者最终矢高均达到0.5 m.

优化结果的拓扑对比：两者的最终拓扑构型较接近，略有不同，但联合优化结果较清晰；拓扑构型显示在均布荷载作用下，结构主要通过对角线方向受力；支座部位颜色较深，表明此处对整个结构的鲁棒性影响较大，应重点加强.

联合优化与单独优化的数据，列于表1中.表中，IR为鲁棒性指标，U为应变能，D为最大位移.

本文采用的优化目标为结构鲁棒性指标，单独优化时先进行形状优化，然后在形状优化基础上进行拓扑优化，得到的鲁棒性指标为5.33×10-3，而联合优化的鲁棒性指标为4.26×10-3，明显优于前述方法，证明了联合优化对寻找最优结构的有效性.结构应变能和最大位移均出现了下降，表明在结构鲁棒性提高的同时，结构的刚度变大.

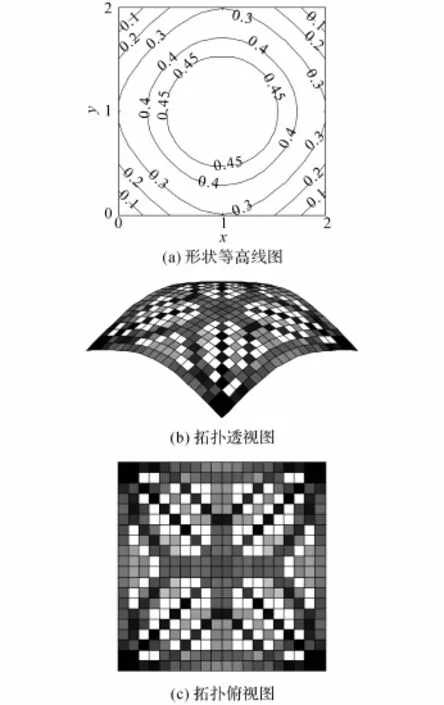
图5 联合优化结果Fig.5 Results of combined optimization

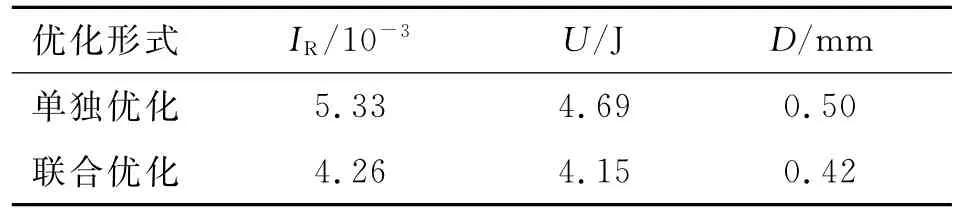
表1 联合优化与单独拓扑优化结果Tab.1 Results of combined optimization and topology optimization

先进行形状优化再进行拓扑优化的方法得到的结构，指标劣于联合优化的原因如下：在单独进行拓扑优化时，结构形状已经确定，故在进行拓扑优化时，形状变量无法改变，不能实现形状、拓扑变量的藕合影响，最优拓扑受到先决形状的限制.之所以形状和拓扑变量要联合优化，是因为两者对优化指标的影响不是线性独立的，而是非线性藕合的；在寻求最优结构时，应采用联合优化的方法，这样才能求解出最优的形状和拓扑.

根据均布荷载作用下联合优化得到的构型，可以设计如图6所示的曲面（更准确地理解为结构的最优传力路径）.可以看出，结构总是试图以最短路径传递荷载，即一个性状良好的结构，传力方式总是简单直接的，这与结构设计的认知是一致的；同时，传力路径呈拱形，且传递路径可以分为对角拱和边界拱，将均布荷载收集传递至支座.

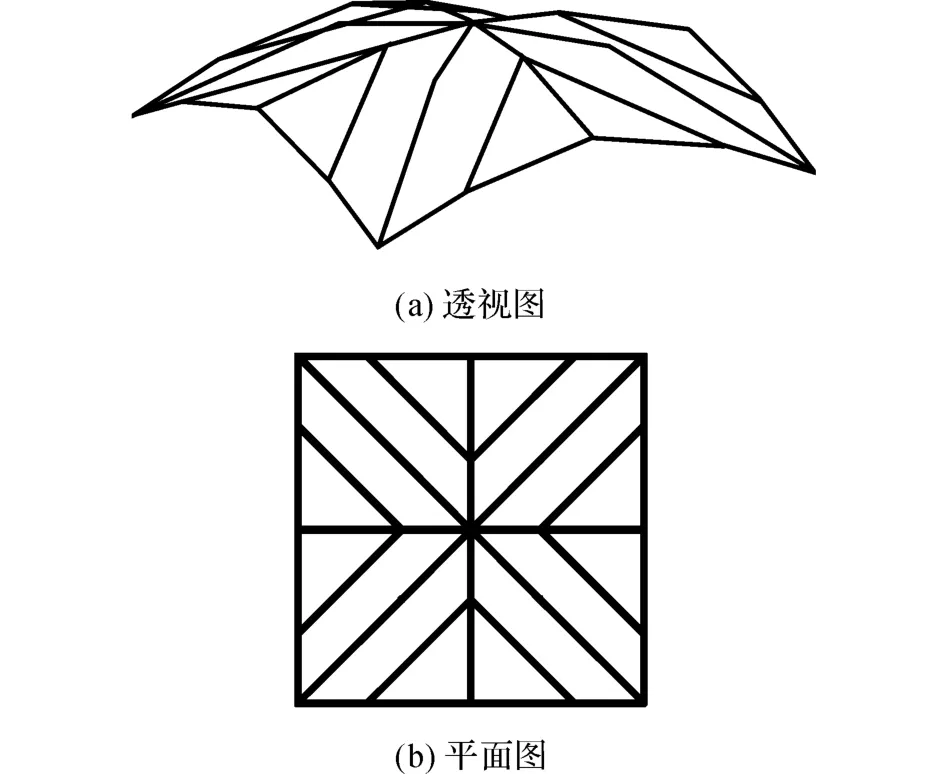
图6 全跨荷载结构主要传力路径Fig.6 Main force travelling path of structure under allcross load

2.2 曲面形状和拓扑联合优化算例分析

2.2.1 半跨荷载作用下角点支承的自由曲面联合优化 为了比较荷载形式对优化结果的影响，将图1改为施加左半边的均布半跨荷载，由于半跨荷载具有1/2对称性，控制点取图4中的2、3、6、7、8、11、12、13、16、17、18、22、23共13个形状变量，在图5下半部共10×20=200个单元中引入SIMP变密度模型，其余条件参考例2.1.DE参数如下：种群NP=500，优化步Iter=400.

图7 优化拓扑透视图Fig.7 Optimized topology perspective

最优的结构形状和材料布局如图7、8所示.在半跨荷载施加的位置，结构上凸，最高点达到0.461，而无荷载的半跨，结构较低缓，这是对半跨荷载最有效的抵抗形状；变密度值的分布集中于左半跨，除了支座部位，右半跨材料较稀疏，单元颜色较深的地方用粗线绘制，单元颜色较浅的地方用细线绘制.可以发现，从荷载中心附近一点发出，与支座相连的4条粗线和3条边界线，是结构的主要传力路径，是材料分布的集中区域.

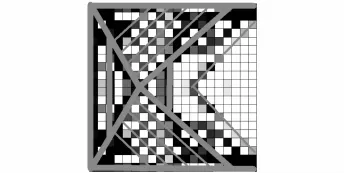
图8 半跨荷载结构主要传力路径Fig.8 Main force travelling path of structure under semi-cross load

2.2.2 集中荷载作用下四边中点支承的自由曲面联合优化 将平面中心位置作用5k N的集中荷载，正方形平面四周边中点支承，由结构1/4对称性，取图4中1、2、6、7、8、12、13共7个控制点作为形状变量，1/4结构单元的SIMP值作为拓扑变量，共有拓扑变量100个，其余条件参考例2.1.DE算法参数如下：NP=250，Iter=300.

优化完成后，曲面形状如图9所示，该曲面的边界保持不变，中心处形成突起，最高点达到0.37；曲面的拓扑构型如图10所示.可以发现，荷载传力路径呈十字型，材料分布集中于荷载作用处以及4个支座位置.

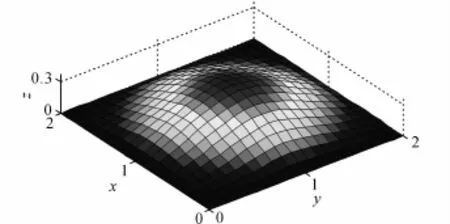
图9 优化后曲面形状Fig.9 Surface after optimization

3 结 论

（1）联合优化与传统单独优化的对比结果表明，形状和拓扑共同影响自由曲面结构的力学性能，两者呈非线性藕合关系.优化数值证明了联合优化后的结构是数学上的全局最优解，而单独优化只是特定条件下的局部最优解.

图10 优化后拓扑Fig.10 Topology after optimization

（2）本文的联合优化结果为自由曲面网格结构的找形和杆件布置提供了依据.尽管拓扑构型不能直接用于实际网格划分，但为网格布置提供了理论依据与参考，可以指导自由曲面的网格划分，明确杆件布置的方向，以满足力流传导的需要.

（3）本文所采用的H∞结构鲁棒性指标是描述结构力学性能的综合指标，反映结构抵抗破坏的能力.本文的算例表明，在结构鲁棒性提高的同时，结构的应变能下降，即结构的刚度提高.

（

）：

[1]崔昌禹，王有宝，姜宝石，等.自由曲面单层网壳结构形态创构方法研究[J].土木工程学报，2013，46（4）：57-63.

CUI Chang-yu，WANG You-bao，JIANG Bao-shi，et al.Study on the structural morphogenesis technique for single-layer reticulated shells of free-curved surface[J].China Civil Engineering Journal，2013，46（4）：57-63.

[2]武岳，李欣，曹正罡.曲线变换型自由曲面结构的形态创建[J].建筑结构学报，2012，33（5）：23-30.

WU Yue，LI Xin，CAO Zheng-gang.Computational morphogenesis method of curve-generated freeform structures[J].Journal of Building Structures，2012，33（5）：23-30.

[3]ESPATH L F R，LINN R V，AWRUCH A M.Shape optimization of shell structures based on NURBS description using automatic differentiation[J].International Journal for Numerical Methods in Engineering，2011，88（7）：613-636.

[4]李娜，岑培超，罗尧治.仿扇贝形体的网壳结构建模及造型优化方法[J].科技通报，2008，24（2）：224-230.

LI Na，CEN Pei-chao，LUO Yao-zhi.Modeling methodof the scallop-shaped lattice shell and optimization with strain energy method[J].Bulletin of Science and Technology，2008，24（2）：224-230.

[5]张峥，丁洁民.大跨度结构的复杂曲面找形技术及工程应用[J].建筑结构，2006，36（3）：5-8.

ZHANG Zheng，DING Jie-min.Form-finding technique and application of complex curved surfaces in large-span structures[J].Journal of Building Structures，2006，36（3）：5-8.

[6]李承铭，卢旦.自由曲面单层网格的智能布局设计研究[J].土木工程学报，2011，44（3）：1-7.

LI Cheng-ming，LU Dan.Study of intelligent layout design of single-layer lattice shell of free form surface[J].China Civil Engineering Journal，2011，44（3）：1-7.

[7]RASMUSSEN M H，STOLPE M.Global optimization of discrete truss topology design problems using a parallel cut-and-branch method[J].Computers and Structures，2008，86（13）：1527-1538.

[8]罗震，陈立平，黄玉盈，等.连续体结构的拓扑优化设计[J].力学进展，2004，34（4）：463-476.

LUO Zhen，CHEN Li-ping，HUANG Yu-ying，et al.Topological optimization design for continuum structures [J].Advances in Mechanics，2004，34（4）：463-476.

[9]ROZVANY G.A critical review of established methods of structural topology optimization[J].Structural and Multidisciplinary Optimization，2009，37（3）：217-237.

[10]WANG Lei，ZHANG Qi-lin，YANG Bin.Combined shape and topology optimization of free form shells[J].Advanced Materials Research，2011，163：2356-2360.

[11]ANSOLA R，CANALES J，TÁRRAGO J A，et al.An integrated approach for shape and topology optimization of shell structures[J].Computers and Structures，2002，80（5）：449-458.

[12]DOYLE J C，GLOVER K，KHARGONEKAR P P，et al.State-space solutions to standard H2and H∞control problems[J].IEEE Transactions on Automatic Control，1989，34（8）：831-847.

[13]梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用[M].北京：清华大学出版社，2008：61-63.

[14]PIEGL L，TILLER W.非均匀有理B样条[M].赵罡，穆国旺，王拉柱，译.2版.北京：清华大学出版社，2010：86-101.

[15]昌俊康，段宝岩.连续体结构拓扑优化的一种改进变密度法及其应用[J].计算力学学报，2009，26（2）：188-192.

CHANG Jun-kang，DUAN Bao-yan.An improved variable density method and application for topology optimization of continuum structures[J].Chinese Journal of Computational Mechanics，2009，26（2）：188-192.

[16]张成，吴慧，高博青，等.基于H∞理论的结构鲁棒性分析[J].建筑结构学报，2012，33（5）：87-92.

ZHANG Cheng，WU Hui，GAO Bo-qing，et al.H∞-based structural robustness analysis[J].Journal of Building Structures，2012，33（5）：87-92.

[17]STORN R，PRICE K.Differential evolution：a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997，11（4）：341-359.

Combined shape and topology optimization of free-form structure

MA Teng1，ZHAO Xing-zhong1，2，GAO Bo-qing1，WU Hui3

（1.Space Structures Research Center，Zhejiang University，Hangzhou 310058，China；2.China IPPR International Engineering Corporation，Beijing100089，China；3.College of Urban/Rural Planning and Management，Zhejiang University of Finance and Economics，Hangzhou 310018，China）

Shape and topology of free-form grid structures were simultaneously considered in order to reach the global optimum shapes and topologies.Optimum structural robustness was set to be the objective while parameters to define the structural shape and topology were taken as design variables.A differential evolution algorithm was used to solve the combined optimization problem.Global optimum shapes and topologies of free-form structures were obtained.The obtained results were compared with those achieved by optimizing solely shape or topology.Results showed that more robust structures with better mechanical properties were obtained，which implied the superiority of the method.The optimized structures were more efficient in carrying the load，and the resulted shape and topology clearly revealed the main force transferring paths.

free-form structure；shape and topology；robustness；combined optimization

TU 393

A

1008-973X（2015）10-1946-06

2014-08-22.浙江大学学报（工学版）网址：www.journals.zju.edu.cn/eng

国家自然科学基金面上项目（51378457）；高等学校博士学科点专项科研基金资助项目（20120101110023）；浙江省自然科学基金资助项目（Y15E08004）.

马腾（1988—），男，硕士，从事大跨度空间结构研究.E-mail：mt001mt@163.com

高博青，男，教授.E-mail：bqgao@zju.edu.cn