小样本条件下可变作用代表值的贝叶斯推断方法

姚继涛， 王旭东

（西安建筑科技大学土木工程学院，陕西西安710055）

小样本条件下可变作用代表值的贝叶斯推断方法

姚继涛， 王旭东

（西安建筑科技大学土木工程学院，陕西西安710055）

为克服工程实际中测试数据不充足的条件下，采用经典统计学方法推断可变作用的代表值时，由统计不确定性导致推断结果偏于冒进的缺点，基于极小值I型分布分位值的线性回归推断方法，提出了小样本条件下可变作用代表值的线性回归推断方法，并以此作为检验其他推断方法精度的基准方法；根据贝叶斯理论，利用分布参数的Jeffreys无信息先验分布，提出可变作用标准值和频遇值的贝叶斯推断方法.应用研究结果表明：贝叶斯推断方法较线性回归推断方法简便且应用范围广，在标准差已知的情况，可给出更优的推断结果；无参数信息时，对于标准值和频遇值的保证率不低于0.90的情况，贝叶斯推断方法均具有较好的精度；相对于其他可信水平，可信水平0.75时推断结果更接近真值，因此，建议取可信水平为0.75.

荷载；代表值；贝叶斯方法；统计推断；小样本容量

可变作用的代表值包括标准值、频遇值和准永久值等［1］，对它们的推断是建立结构设计与评定方法的基础.当样本容量（测试数据数量）充足时，一般可采用矩法、极大似然法等经典统计学的推断方法，但实际中的测试数据不总是充足的，如仍采用目前经典统计学的方法，往往导致代表值的推断结果因统计不确定性的影响而偏于冒进，这时更合理的选择是采用小样本的推断方法.

可变作用的任意时点值通常服从极大值Ⅰ型分布，其代表值一般可表达为该分布的某一分位值［2-3］.由于极大值Ⅰ型分布与极小值Ⅰ型分布同属于极值参数分布族，可相互转换［4］，因此，对可变作用代表值的推断可借用目前极小值Ⅰ型分布分位值的线性回归推断方法［5］.该法可在不同的置信度下考虑统计不确定性的影响，用于小样本的场合，在机械、电子等领域产品寿命的推断中有着广泛的应用［6-7］.但是，采用该法推断时需查表确定大量系数的数值，应用不便，且目前的数值表并不完全满足可变作用代表值推断的需要［8］，而建立新的数值表又需进行繁琐的数值计算或蒙特卡洛模拟，存在较大的困难.因此，这种方法不能很好地解决小样本条件下可变作用代表值的推断问题.

小样本条件下，贝叶斯法也是一种可选择的推断方法［9］，除了考虑经典统计学中的总体信息和样本信息，它还考虑了关于总体的先验信息［10］.如果对总体的分布参数采用无信息的先验分布，降低主观因素的影响，则贝叶斯法同样可在小样本条件下给出合理的推断结果，且较线性回归推断方法简便，也便于在更广的范围内使用［11-12］.但是，目前的贝叶斯推断方法主要适用于总体服从二项分布、泊松分布、正态分布、指数分布等的场合，对于服从极大值Ⅰ型分布的总体，目前尚无合适的推断方法［13］.因此，小样本条件下对可变作用代表值的推断需采用新的贝叶斯方法.

本文将首先建立和评价可变作用代表值的线性回归推断方法，并以此作为检验其他推断方法精度的基准方法；然后，重点研究和建立可变作用代表值的贝叶斯推断方法，并通过对比分析评价其优劣.由于可变作用的准永久值一般为可变作用任意时点分布的均值［1］，受统计不确定性的影响较小，可采用经典统计学的方法推断，因此，论文将主要研究可变作用标准值和频遇值的推断问题.

1 线性回归推断方法

一般假定可变作用的任意时点值X服从极大值Ⅰ型分布［2］，其概率密度函数为

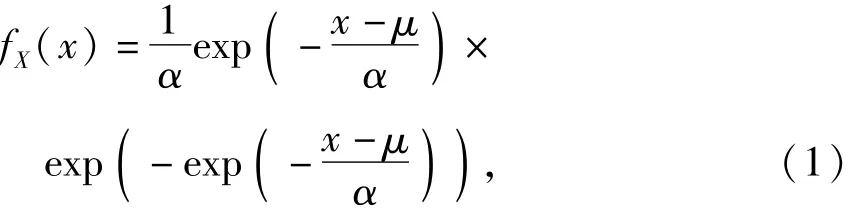
式中：μ、α为分布参数，－∞＜μ＜∞，0＜α＜∞.

可变作用的标准值或频遇值可表示为X的下侧p分位值xp［1］，它满足

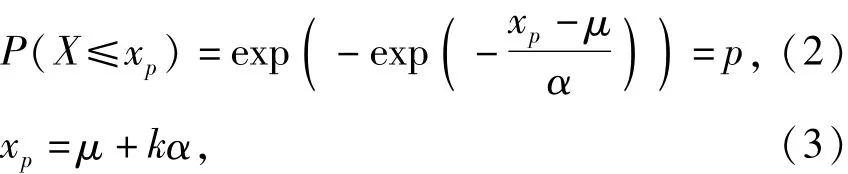
式中：p为标准值或频遇值的保证率，通常取［0，1］内较大的数值；

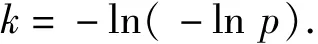
为借用极小值Ⅰ型分布分位值的线性回归推断方法，设X的n个次序统计量（由小到大排列的样本）为X（1），X（2），…，X（n），相应的测试值为x（1），x（2），…，x（n），并令

则Y服从参数为－μ、α的极小值Ⅰ型分布，其次序统计量和上侧p分位值分别为

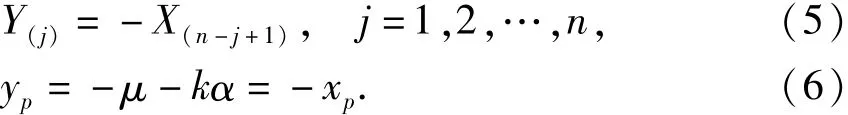
根据极小值Ⅰ型分布分位值的线性回归推断方法［14］，在置信度C下yp的估计量为

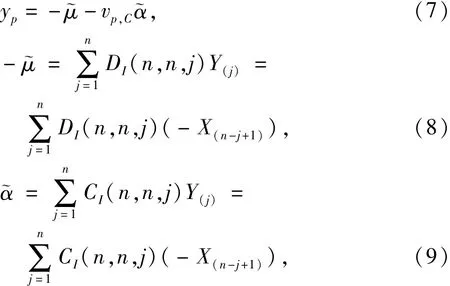
DI（n，n，j）、CI（n，n，j）为仅与样本容量n、样本序位j有关的系数；

vp，C为统计量的下侧C分位值.

DI（n，n，j）、CI（n，n，j）、vp，C均可查表确定［8］.由于

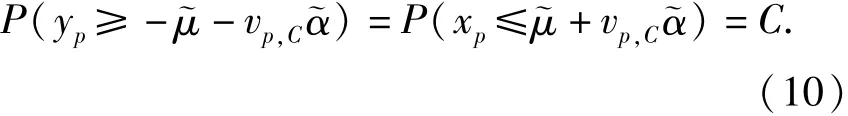
故置信度C下可变作用标准值或频遇值xp的估计量为

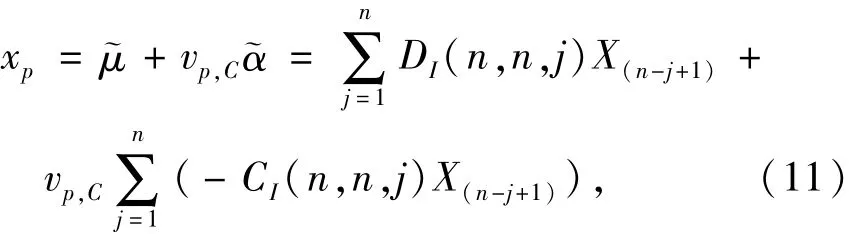
这时根据测试值x（1），x（2），…，x（n），便可最终确定xp的估计值.

该线性回归推断方法不仅考虑了样本容量，还考虑了样本序位，更充分地利用了样本提供的信息，并可在不同的置信度下考虑统计不确定性的影响，适用于小样本场合.但是，该法在应用中需查表确定DI（n，n，j）、CI（n，n，j）、vp，C的数值，查阅过程非常繁琐，且目前vp，C数值表中仅提供了p＝0.90，0.95，0.99和n≤25时的数值［8］，并不完全满足可变作用标准值和频遇值推断的需要，而建立新的数值表又需进行大量的数值模拟计算，存在较大的困难.另外，目前仅建立了无参数信息时的线性回归推断方法，对于标准差已知的场合，尚无相应的方法［14］.

2 贝叶斯推断方法

2.1 无参数信息时的情况

设可变作用任意时点值X的n个样本测试值为x1，x2，…，xn，样本均值和样本标准差分别为x¯和s，则它们发生的联合概率密度函数为

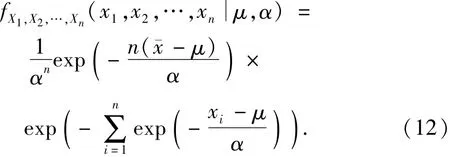
取未知参数μ、α的先验分布为Jeffreys无信息先验分布［13］，即

则μ、α的联合后验分布为

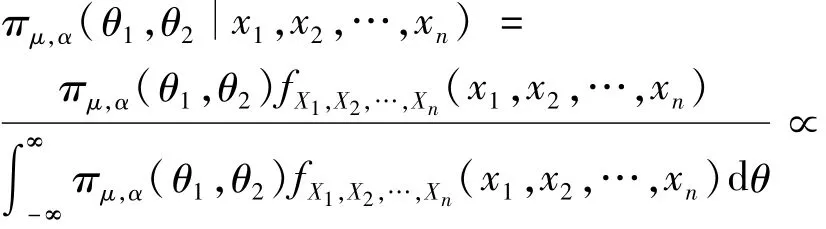
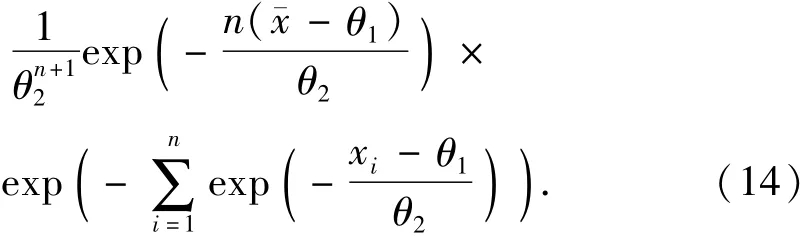
按式（3）进行变量代换后，可得xp、α的联合后验分布为

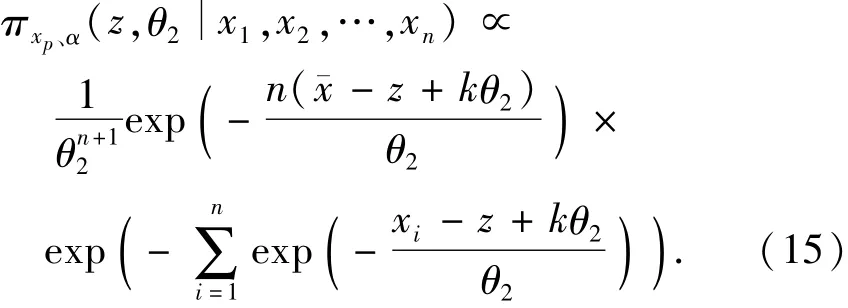
为简化问题，将式（15）中的指数函数近似表达为泰勒级数中的线性项，即

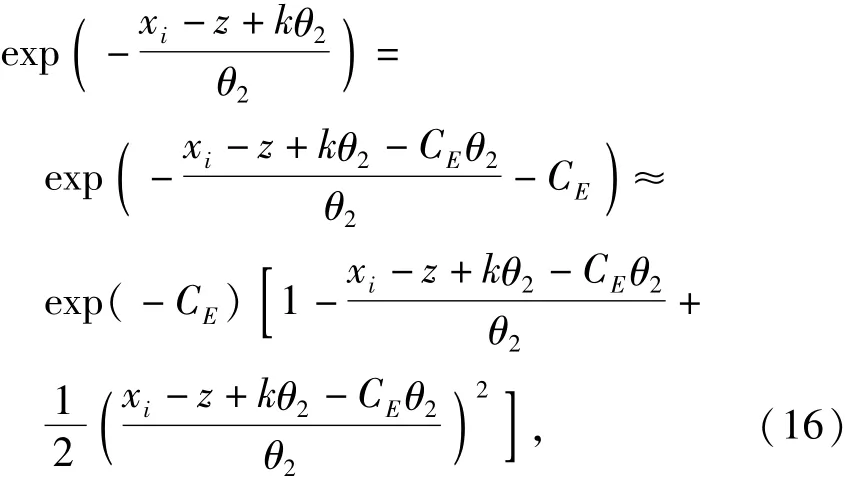
式中：欧拉常数CE≈0.577 2，展开点为（xi－xp＋kα－CEα）／α＝0.

由于X的均值

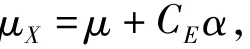
在展开点处有xi－μX＝0，将式（16）代入式（15）并求和可获得相对精确的结果.这时xp、α的联合后验分布可整理为

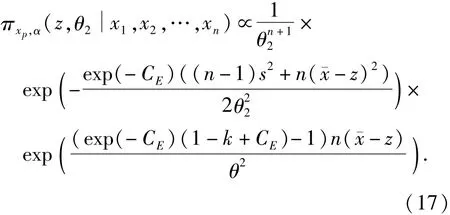
将式（17）中的最后一项按泰勒级数展开，即

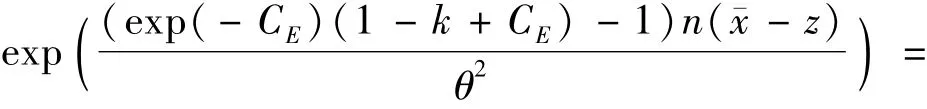
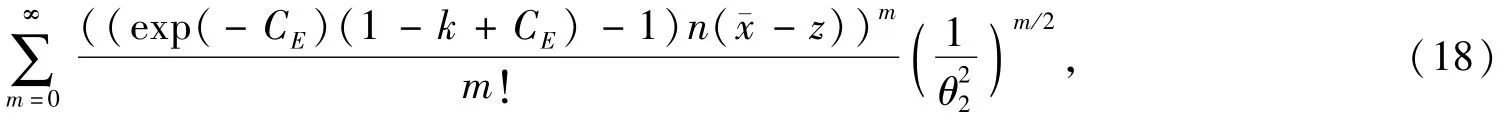
并令

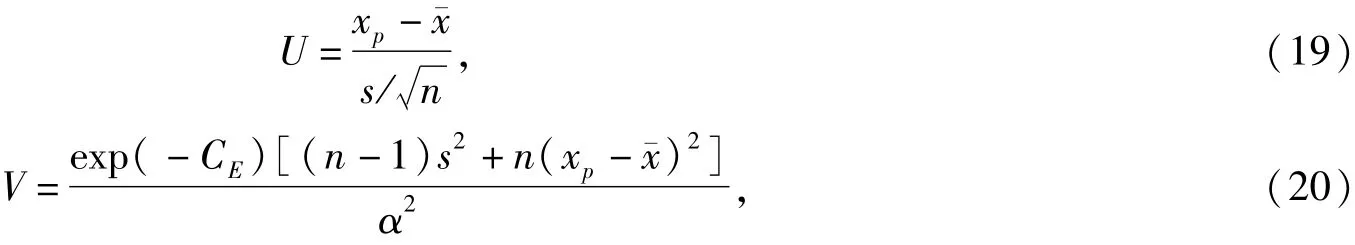
则U，V的联合分布为

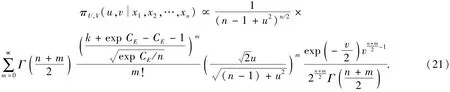
式（21）中最后一个分式为自由度n＋m的χ2分布的概率密度函数［4］.对v积分后，可得U的边缘分布

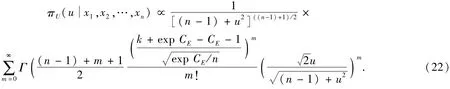
故U服从自由度n－1、参数λ的非中心t分布［4］，

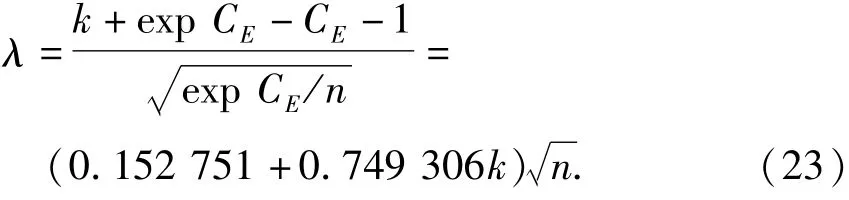
按区间估计法中的上限估计值，最终可得可变作用标准值或频遇值的估计值，即

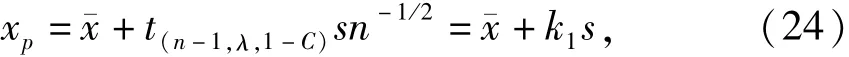
式中：t（n－1，λ，1－C）为自由度n－1、参数λ的非中心t分布的上侧1－C分位值，C为可信水平；

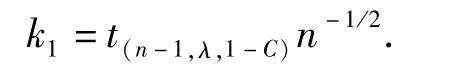
由于目前t（n－1，λ，1－C）的数值表中所考虑的参数λ不能满足标准值和频遇值推断的需要，可采用下列方法近似计算t（n－1，λ，1－C）的值［15］，

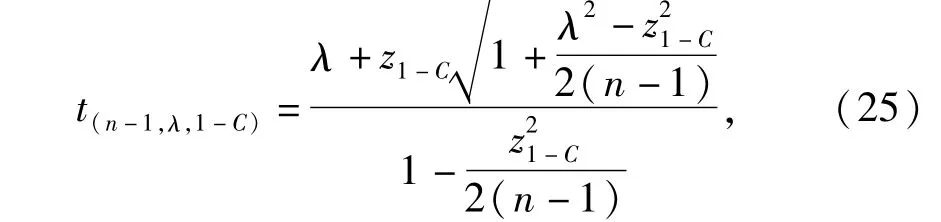
式中：z1－C为标准正态分布的上侧1－C分位值.

2.2 标准差σX已知的情况

可变作用任意时点值X的标准差σX已知时，分布参数同样取未知参数μ的先验分布为Jeffreys无信息先验分布［13］，即

则按贝叶斯公式变量代换后，可得分位值xp的后验分布为

令

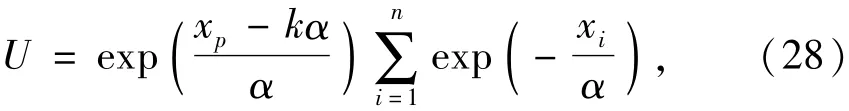
则U的分布为

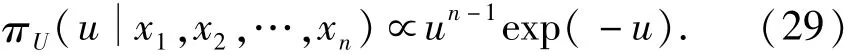
故U服从参数为n的标准伽马分布Ga（n，1）［4］.这时按区间估计法中的上限估计值，可得可变作用标准值或频遇值的估计值，即

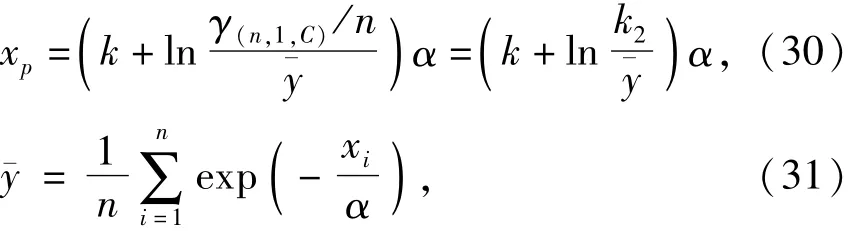
式中：γ（n，1，C）为标准伽马分布Ga（n，1）的下侧C分位值，C为可信水平；k2＝γ（n，1，C）／n.

这时的贝叶斯推断方法在建立过程中并未采用近似手段.

3 对比分析

可变作用标准值和频遇值的保证率p一般均不低于0.90［1-2］，如对风、雪荷载，p＝0.98（标准值）和0.90（频遇值）［16］，因此，仅针对p≥0.90的情况对比分析贝叶斯推断方法的精度.设可变作用任意时点值X的10个次序统计量的测试值为x（1），x（2），…，x（10）（见表1），其统计结果为

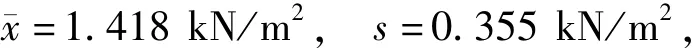
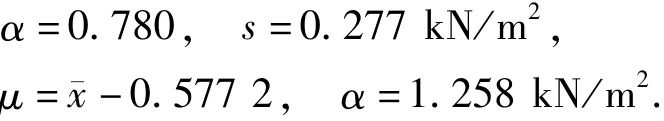
为便于对比分析，设xp的保证率p为目前vp，C数值表中的0.90、0.95和0.99，且σX已知时取σX＝s.

表2列举了不同可信水平C和保证率p下xp的推断结果，推断过程中DI（10，10，j）、CI（10，10，j）的数值及相关计算结果见表1.

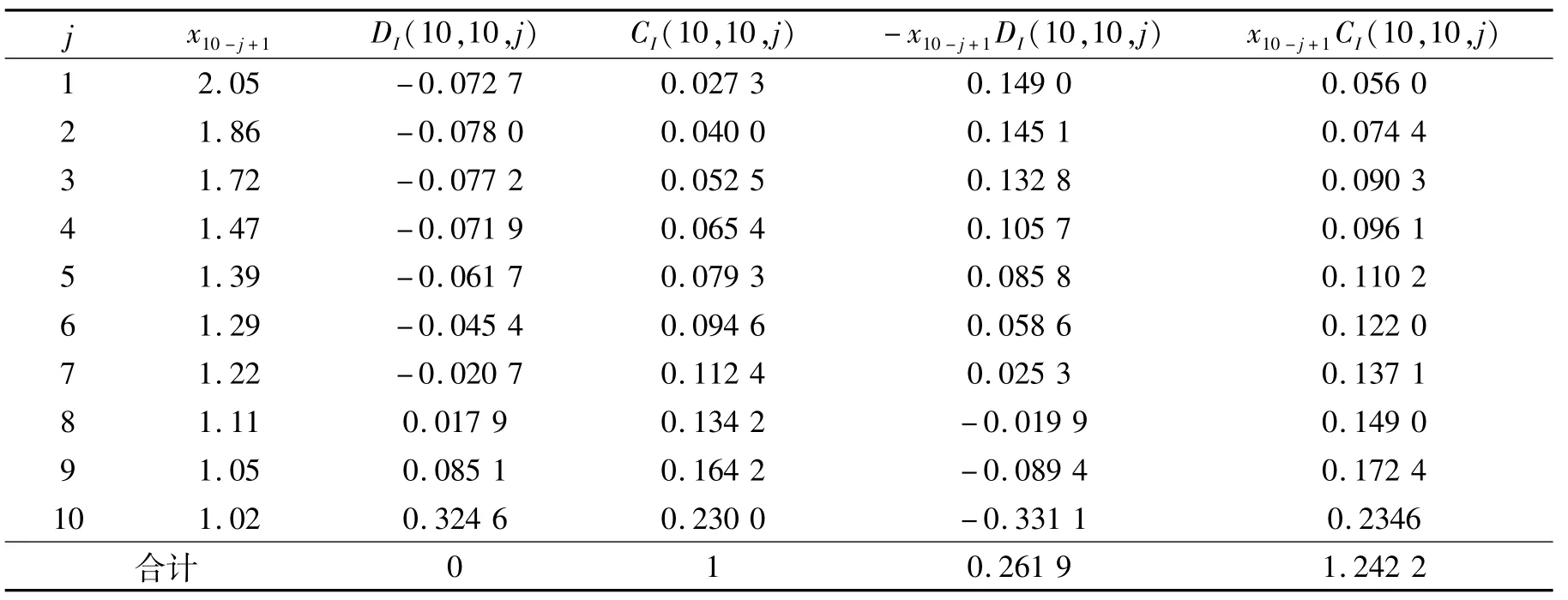
表1 样本测试值和DI（10，10，j）、CI（10，10，j）的值Tab.1 Test values of sample and values of DI（10，10，j），CI（10，10，j） kN／m

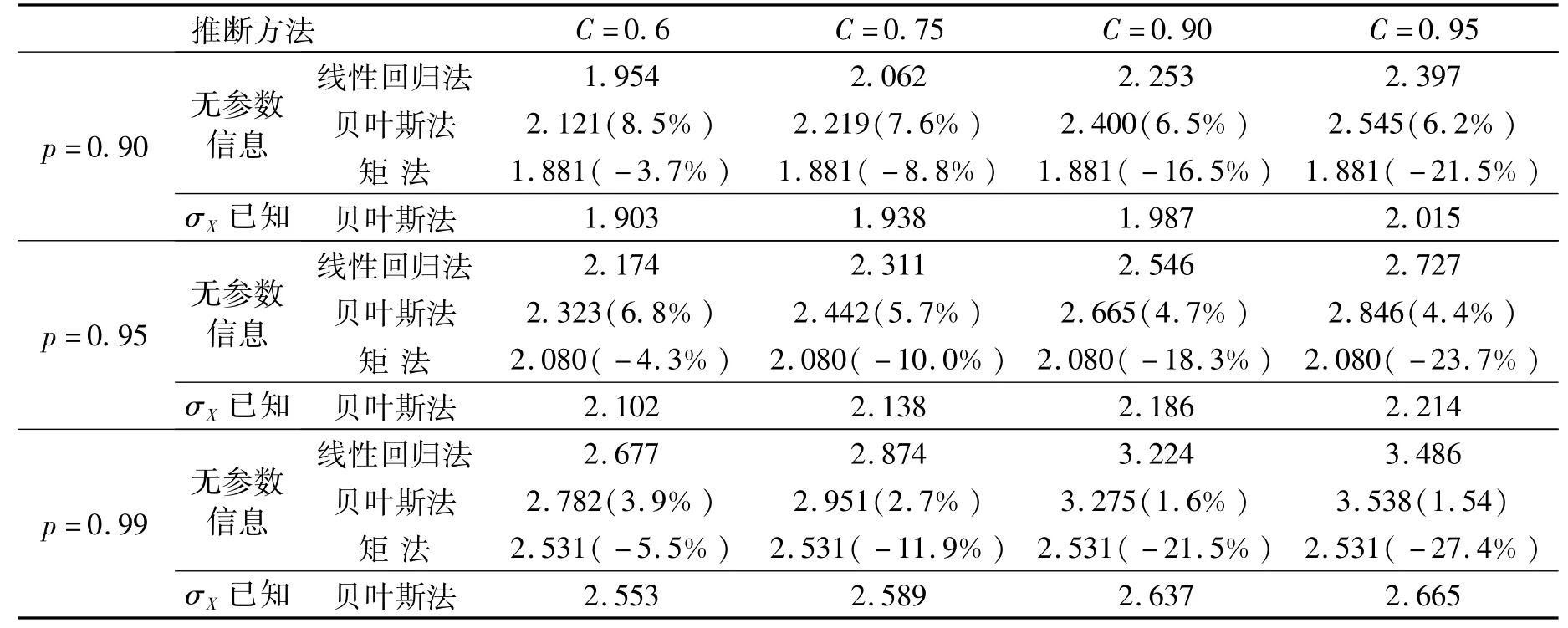
表2 xp的推断结果Tab.2 The inference result of xp

由表2中的结果可知：矩法的推断结果最低，偏于冒进，且C越高，与其它方法的差异越大，这主要是因为未充分考虑小样本条件下统计不确定性的影响；无参数信息时，采用近似展开式的贝叶斯法的推断结果精度较高，且p、C越高，相对误差越小，并偏于保守，适用于任意保证率不低于0.90的情况；σX已知时，贝叶斯法的推断结果因获知更多的参数信息而优于无参数信息时的结果，包括线性回归推断方法的结果，且p、C越高，优势越明显，因此，当σX未知时，可对σX取一个偏大的值，按σX已知时的方法推断.研究中还对比分析了样本容量分别为5和20时，不同p、C值的推断结果，可得到同样的结论.

无参数信息时贝叶斯推断方法的误差主要来源于式（16）所采用的近似方法.按该式可将μ、α的联合后验分布整理为

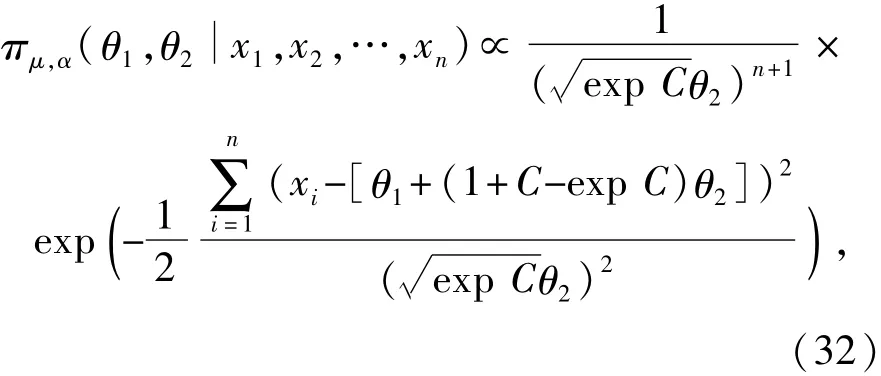
式（32）实际上为正态分布N（μ′，σ′2）的分布参数μ′、σ′的联合后验分布，其中

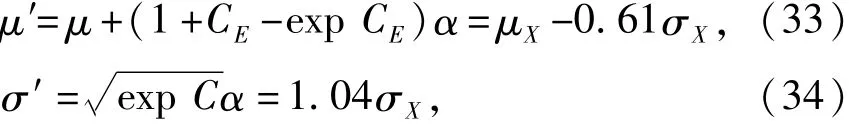
这相当于以正态分布N（μ′，σ′2）替代了原先的极大值Ⅰ型分布.由于极大值Ⅰ型分布、正态分布在概率密度函数曲线的右端更为相似，因此，在推断保证率p较高的分位值xp时可获得相对精确的结果.

由表2中的结果还可知，C≥0.90时，贝叶斯法的推断结果要明显高于矩法的推断结果，且对C的变化敏感；相对而言，C＝0.60，0.75时的推断结果较适宜，且两者的数值差别不大，但按C＝0.75推断时可更充分地考虑统计不确定性的影响，相对误差也更小，因此，相对其他可信水平，按C＝0.75推断可获得更合适的结果，建议取

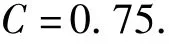
为便于应用，表3列举了可信水平C＝0.75时的k1、k2值.

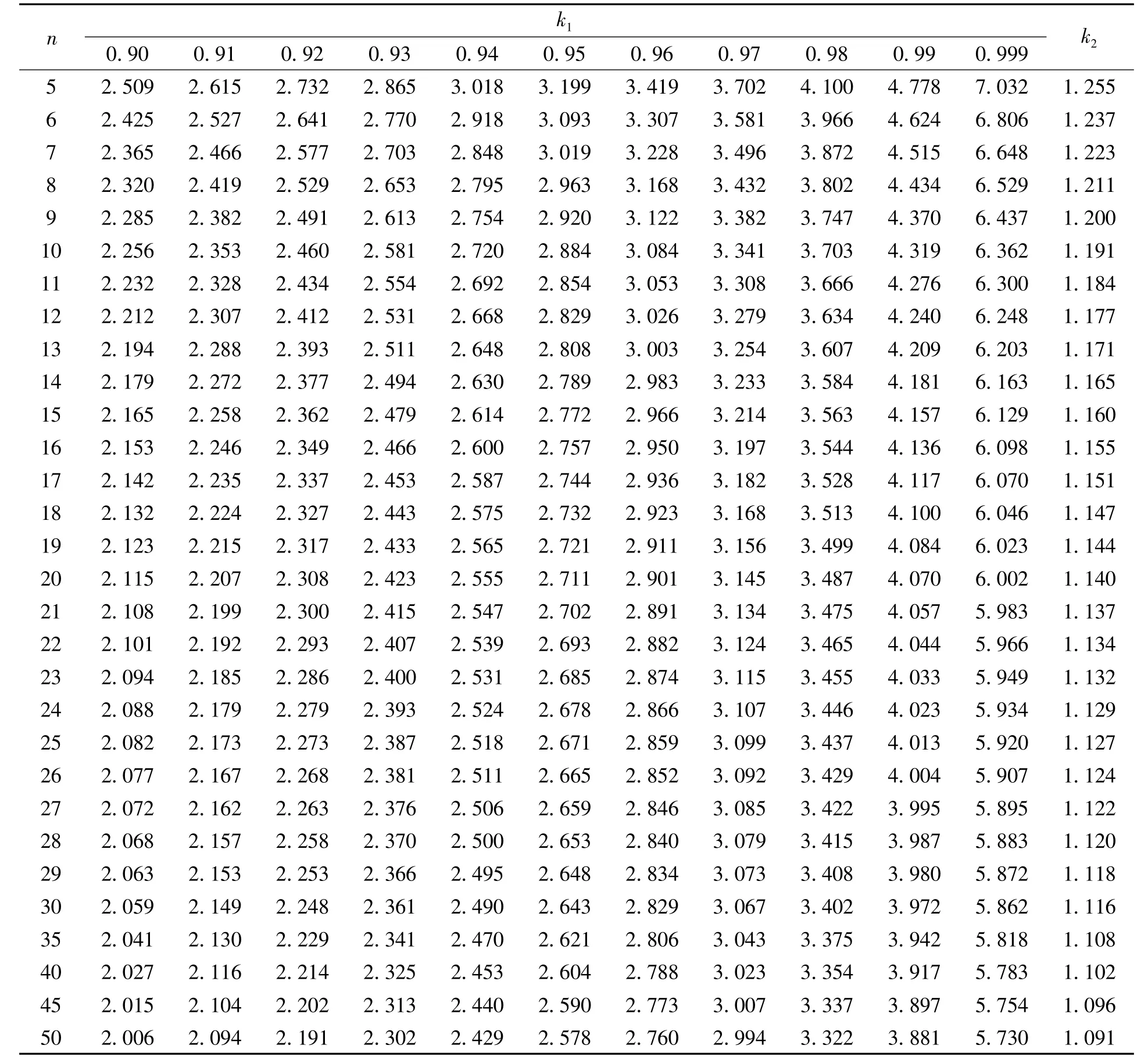
表3 k1、k2数值表（C＝0.75）Tab.3 Numerical tables of k1and k2（C＝0.75）

4 结 论

（1）测试数据不足时，对可变作用准永久值的推断可采用经典统计学的方法，但推断标准值和频遇值时，经典统计学方法的推断结果偏于冒进，它未充分考虑小样本条件下统计不确定性的影响.

（2）小样本条件下，可借用极小值Ⅰ型分布分位值的线性回归推断方法，推断可变作用的标准值和频遇值，但需查表确定大量系数的数值，应用不便，且目前的数值表不能完全满足推断的需要.

（3）用本文中的贝叶斯推断方法，同样可在小样本条件下推断可变作用的标准值和频遇值，但较线性回归推断方法简便，适用范围更广且在标准差已知的情况下，可给出更精确的推断结果.

（4）无参数信息时，对于保证率不低于0.90的情况，文中贝叶斯推断方法得到的可变作用标准值和频遇值具有较高的精度.

（5）相对于其他可信水平，贝叶斯推断方法在可信水平为0.75时的推断结果要更为合适，建议取可信水平为0.75.

［1］ 中国建筑科学研究院.GB50153—2008工程结构可靠性设计统一标准［S］.北京：中国建筑工业出版社，2009.

［2］ 中国建筑科学研究院.GBJ68—84建筑结构设计统一标准［S］.北京：中国建筑工业出版社，1984.

［3］ 冯云芬，贡金鑫，王建超.楼面活荷载、风荷载的频遇值和准永久值的确定［J］.工业建筑，2012，42（7）：74-78.FENGYunfen，GONGJinxin，WANGJianchao.Determination of frequent value and quasi-permanent value of floor live load and wind load［J］.Industrial Construction，2012，42（7）：74-78.

［4］ 茆诗松.统计手册［M］.北京：科学出版社，2003：212-223.

［5］ 周源泉.质量可靠性增长与评定方法［M］.北京：北京航空航天大学出版社，1997：151-174.

［6］ 黄炎生，邓浩，李涛.考虑验证荷载的既有结构可靠度计算［J］.华南理工大学学报：自然科学版，2008，36（10）：12-15.HUANG Yansheng，DENG Hao，LI Tao.Reliability calculation of existing structure under proof load［J］.JournalofSouthChinaUniversityofTechnology：Natural Science Edition，2008，36（10）：12-15.

［7］ AGGARWALA R.Progressive interval censoring：some mathematicalresultsapplicationtoinference［J］.Communications in Statistics：Theory and Methods，2001，30：1921-1935.

［8］ 第四机械工业部标准化研究所.可靠性试验用表［M］.北京：国防工业出版社，1979：1-87.

［9］ CHOPIN N，LELIÈVRE T，STOLTZ G.Free energy methods for Bayesian inference：efficient exploration of univariateGaussianmixtureposteriors［J］.Stat.Comput，2012，22：897-916.

［10］ TSIONAS E G.Bayesian inference for multivariate gamma distributions［J］.Statistics and Computing，2004，14（3）：223-233.

［11］ PENG Xiuyun，YAN Zaizai.Bayesian estimation for generalizedexponentialdistributionbasedon progressivetype-Ⅰintervalcensoring［J］.Acta Mathematicae Applicatae Sinica，2013，29（2）：391-402.

［12］ LIN YJ，LIOYL.Bayesianinferenceunder progressive type-Ⅰinterval censoring［J］.Journal of Applied Statistics，2012，39（1）：1811-1824.

［13］ 茆诗松.贝叶斯统计［M］.北京：中国统计出版社，1999：75-79.

［14］ 戴树森，费鹤良.可靠性试验及其统计分析（上册）［M］.北京：国防工业出版社出版，1983：617-628.

［15］ 姚继涛.基于不确定性推理的既有结构可靠性评定［M］.北京：科学出版社，2011：50-57.

［16］ 中国建筑科学研究院.GB50009—2001建筑结构荷载规范［S］.北京：中国建筑工业出版社，2001.

（中文编辑：秦萍玲 英文编辑：兰俊思）

Bayesian Methods for Inferring Representative Values of Variable Actions in Small Sample Situations

YAO Jitao， WANG Xudong
（School of Civil Engineering，Xi'an University of Architecture and Technology，Xi'an 710055，China）

There is a need sometimes in engineering to infer the representative values of variable actions in cases when the test data is not sufficient，but the classical statistics methods do not take into account of the succedent influences of statistical uncertainty，and the inferred results are always on the aggressive side.In order to overcome the above shortcomings，applying the current linear regression estimation for inferring the fractiles of type I minimum distribution，the linear regression estimation of representative values of variable actions is proposed as a reference method for the precision inspection of other inference methods.According to Bayesian theory，applying Jeffreys non-informative prior distribution，a Bayesian method for inferring characteristic and frequent values of variable actions is put forward.The results show that the Bayesian inference method is more convenient than the liner regression estimation，and easy to use in a broader context.The method can give more advantageous results when standard deviation is known.If no parameter information is available，the Bayesian inference method has better precision when the guarantee rates of characteristic and frequent values are no less than 0.90.Compared with other confidence degrees，the inferred results are more close to the true value when the confidence degree equals 0.75；therefore，it is recommended to take a confidence degree of 0.75.

load；characteristic value；Bayesian approach；statistical inference；small sample

TU312.1

：A

0258-2724（2014）06-0995-07

10.3969／j.issn.0258-2724.2014.06.010

2013-09-29

国家自然科学基金资助项目（50678143，51278401）

姚继涛（1965－），男，教授，博士，研究方向为结构可靠性理论，电话：029-82202359，E-mail：yaojitao＠163.com

姚继涛，王旭东.小样本条件下可变作用代表值的贝叶斯推断方法［J］.西南交通大学学报，2014，49（6）：995-1001.