马克思生产力学说之数理诠释

曾尔曼

马克思生产力学说之数理诠释

曾尔曼

本研究旨在以定量的马克思生产函数体系包括劳动价值理论方程与剩余价值理论方程,借鉴牛顿力学原理，尝试建立马克思关于生产力的数理解析模型；运用变分法解析生产力发展之最优路径。马克思关于两大部类生产有计划按比例的条件，既有静态的关联、又是动态的均衡。生产力发展的本质是基于分工深化的生产迂回度增加，资本有机构成水平不断下降，核心是可变资本即人力资本的持续深化。

马克思劳动价值论方程与社会生产率

根据前期研究结果1建立的马克思价值理论函数体系：

得到马克思劳动价值论方程：

于是，凝聚在商品中的价值量决定于：（社会）必要劳动时间t、生产资料C、劳动力L投入w、生产的组织形式暨生产的迂回度2dR与（社会）生产率的增长率f！

马克思剩余价值论方程与规模收益递增

类似地，

利润率与资本有机构成正相关,

利润率与剩余价值率的增长率均与资本有机构成的增长率成正比;规模收益递增与劳动分工的水平成正比，只要资本有机构成的增长率为正数，生产的规模收益实现递增。

马克思生产函数与经济均衡3

可见，投入Cv产出Y的增长率之差正是生产率的增长率f！

马克思在《资本论》中论述了生产资料与生活资料两大部类的产品生产交换应满足：，也就是：

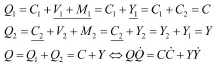
从马克思生产力函数体系可直接得到：

即：如果部类I的投入（C）与部类II的产出（Y=V+M）完全充分交换，说明了还存在动态均衡。经济危机周期取决于两部类生产资料的投资增长率之差：

生产力的解析表达式

马克思在《德意志意识形态》中阐述了一个民族的生产力发展水平取决于分工的程度；在《雇佣劳动与资本》指出中，“增加劳动的生产力的首要办法是更细地分工，更全面地运用和改进机器”，后者无疑反映为资本有机构成的增长。科学技术以劳动分工为本质就是第一生产力！结合以上分析，生产力就可以根据：

表征为分工系数与资本有机构成增长率之积：

生产力最优发展的条件是没有剥削！该条件也可通过对马克思生产函数Y与劳动价值论方程Q运用变分法得到：

马克思最优增长与“无增长的繁荣”

前期运用变分法于成本函数得到了关于投入最少的经济最优增长路径：

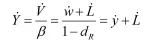
在稳态下，经济增长为0：

而劳动生产率y与人均工资率w的增长就决定于企业数与企业人均就业量的增长率：

法国经济学家托马斯·皮克迪(Thomas Piketty)对自18世纪工业革命至今300来年多国可以观察到的财富分配数据进行分析：投资回报平均维持在每年4%-5%，而GDP平均每年增长1%-2%，认为资本回报率总是倾向于高于经济增长率，也即：，从另一角度看，正是说明经济的可持续发展要求投入增长率低于一阈值！

最优税率：

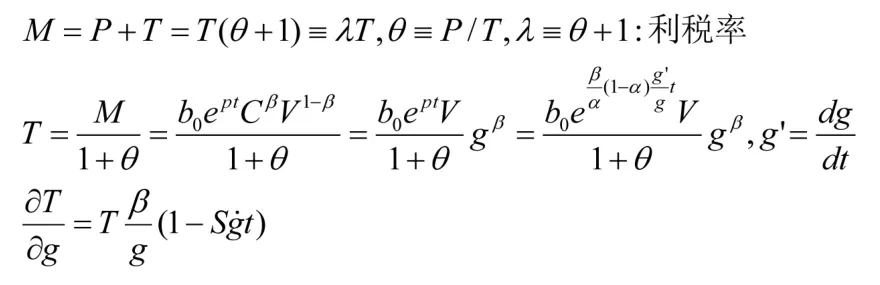
（作者单位：厦门产业技术研究院）

[1]曾尔曼：《马克思生产力经济学导引》，厦门大学出版社，2013

[2]Young AA.Increasing Returns and Economic Progress [J].The Economic Journal,1928,38:527-42

[3]曾尔曼：《厦门科技》2014（3）31