V型肋片直冷却通道内流动与传热的数值研究

张艾萍，毕帅，付磊，陈德，卢贺，沈忠良

(东北电力大学能源与动力学院，吉林吉林132012)

V型肋片直冷却通道内流动与传热的数值研究

张艾萍，毕帅，付磊，陈德，卢贺，沈忠良

(东北电力大学能源与动力学院，吉林吉林132012)

采用结构化六面体网格和k-ε湍流模型求解三维N-S方程，对内置不同肋间距与肋高比V型扰流肋片的直冷却通道，在入口雷诺数为20 000时的流动与换热特性进行数值模拟，分析了不同肋间距与肋高比对肋间壁面换热效果和流动损失的影响，并对肋间距与肋高比进行了全局寻优。结果表明，带肋直冷却通道的整体换热效果和综合冷却效率，分别和肋间距与肋高比呈近似函数关系，肋间距与肋高比为7.93时通道整体换热效果最好，为5.2时通道综合冷却效率最佳。

燃气轮机；涡轮叶片；冷却；扰流肋；肋间距与肋高比；全局寻优

1 引言

现代燃气轮机不断增高的涡轮入口温度，已达到甚至超过金属材料的温度极限，因此须采用有效的冷却技术，来保证燃气轮机涡轮叶片的运行安全和合理寿命[1]。带肋通道作为一种简单有效的冷却方式，可以增大换热面积及对冷却气流的扰动，增强换热效果，在燃气轮机中得到广泛应用。因此，研究带肋通道的换热特性，对燃气轮机涡轮动叶冷却机构设计具有重要意义。

Han等通过实验和数值模拟研究了带肋通道中的空气流动和换热过程，分析了肋的排列形式、形状，肋片导流角，肋间距与肋高比和通道宽高比等几何参数及雷诺数对换热效果的影响[2-7]。Huh等[8]在不同雷诺数下，对几种肋间距矩形通道的换热效果进行了研究。Liu等[9]对矩形截面的U型通道进行了实验研究，实验选取矩形通道宽高比为1/2，肋间距与肋高比分别为3.0、5.0、7.5、10.0。结果显示，肋间距与肋高比为3.0时的换热性能最好，5.0时的压力损失最大。张勃等[10]研究了肋宽与肋间距比和肋宽与肋高比，对网格式肋化通道换热和总压损失的影响，实验模型选取的肋宽与肋高比分别为0.25、0.30、0.50，肋宽与肋间距比分别为0.25、0.33、0.50。结果显示，肋宽与肋高比为0.30、肋宽与肋间距比为0.50的模型的换热效果最好，但同时压损也最大。杨阳[11]针对弯折通道中不同节距-肋高比所造成的换热特性不同进行了数值研究，模型选取的节距-肋高比分别为3、5、7、8、9、10、12和14。研究表明，最佳的节距-肋高比应在7～10之间，在此区间内，肋后分离区在与主流作用中呈现周期脱落与主流掺混，明显提高了分离区后的换热效果。

以上叶片冷却研究都是先选取几个离散的几何设计变量进行实验或数值计算，然后对比选出其中的最佳值，不能保证设计值的全局寻优。鉴于此，本文采用数值模拟方法，研究V型肋片不同肋间距与肋高比下直冷却通道的换热和流动，然后对计算结果用MATLAB粒子群寻优算法进行全局寻优，得出通道整体换热效果最好和综合换热效率最佳的设计参数。

2 计算模型和计算方法

2.1 计算模型

运用UG参数化建模方法对动叶通道进行简化处理，采用文献[6]中的几何模型参数建立带V型扰流肋片的直通道模型。图1是具有对称性的一半冷却通道的物理模型示意图。

图1 冷却通道物理模型示意图Fig.1 Schematic diagram of physical model

计算模型(图2)为内置V型肋片的方形通道，冷却通道上下壁面沿流动方向布置V型肋片。肋片导流角α=45°，肋高e=1.6 mm，肋高与当量直径Dh之比为0.078:1，肋宽与肋高之比为1:1，直通道高H=12.7 mm，宽W=50.8 mm。通道入口雷诺数Re=20 000。

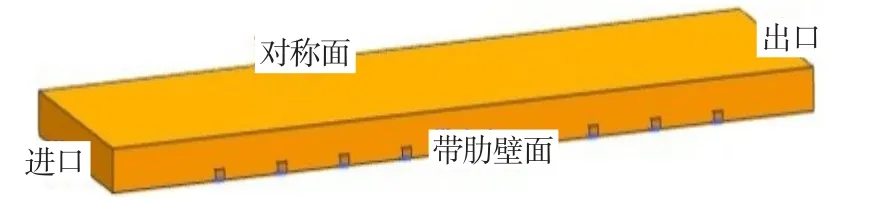
图2 计算模型示意图Fig.2 Schematic diagram of computational model

在此模型的基础上，对肋间距变化时直冷却通道的流动与换热特性进行计算。肋间距与肋宽比P/e取值范围为3～14共12个算例，其他几何及计算参数相同。

2.2 网格独立性验证和湍流模型选取

分别采用约50万、65万、80万、95万网格进行计算，结果表明网格数超过65万后各计算结果基本无变化，因此下面均采用80万网格进行计算。图3示出了ANSYSk-ε、k-ω和SST三种湍流模型在Re=20 000的模拟结果，与文献[6]实验数据的对比。可见，k-ω和SST模型的计算结果与实验数据偏差较大，而k-ε湍流模型与实验数据吻合较好，能更准确地模拟带肋通道的流动与换热，故本文采用k-ε湍流模型进行计算。

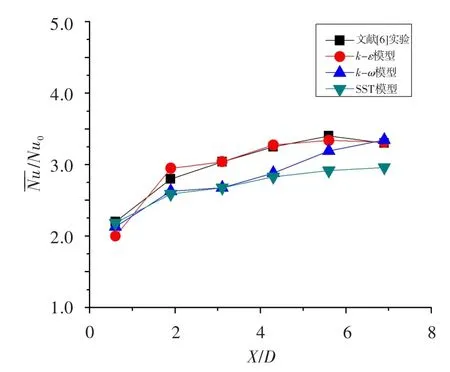
图3 不同湍流模型的/Nu0与实验数据的对比Fig.3/Nu0and experimental data of different turbulence models

2.3 数值计算方法

采用有限体积法及全隐式方法用ANSYS软件求解三维定常粘性N-S方程，计算采用二阶高精度差分格式，计算收敛的平均残差小于10-5，保证计算质量。计算网格采用ICEM结构化六面体网格形式，主要换热在肋间壁面的y+值小于2，重点求解部分局部加密。带肋直通道的网格示意图如图4所示。

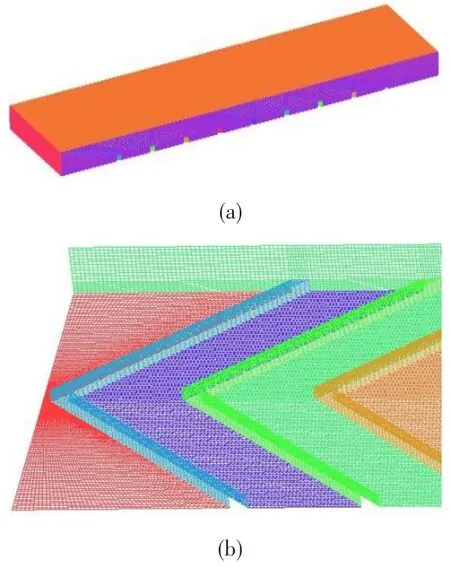
图4 带V型肋直冷却通道计算网格Fig.4 Computation mesh of V-shaped disturbed flow rib

计算模型边界条件采用文献[6]中的参数。进口设置为速度进口，湍流度为5%，冷却介质为空气，给定Re=20 000时相对应的法向速度；出口设置为压力出口，静压101 325 Pa。计算区域上下带肋壁面热流密度q给为定值，其中顶面设置为直通道对称面，左右壁面均为绝热表面。

3 计算结果与分析

采用无量纲努赛尔数来衡量换热效果。冷却通道的平均对流换热系数h=q/(Tw-Tf)，平均努赛尔数。其中h按光滑通道计算，Tw为冷却通道上下壁面的平均温度，Tf为冷却通道进口冷却空气的平均温度，Dh=2HW/(H+W)，λ为冷却介质的导热系数。

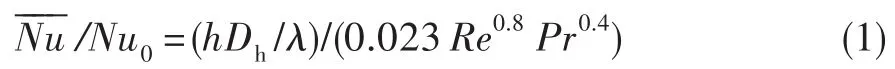
式中：Pr为冷却介质的普朗特数。

3.1 流动与传热特性

对上述12种不同P/e值在相同边界条件下进行数值模拟，对计算所得的和P/e通过MATLAB软件拟合得到的函数曲线如图5所示，然后在该参数范围内寻优。

图5 肋间距与肋高比和平均努赛尔数的拟合曲线Fig.5 Fitted curve for the ratio of rib spacing and rib height and averaged Nusselt number

运用粒子群算法在P/e=3～14范围内寻优，得到当P/e=7.93时带肋壁面的为最大，整体换热效果最好。通过ANSYS模拟计算P/e=5.2时得到，数值模拟结果与寻优结果误差较小，寻优结果可靠度较高。

图6为不同P/e时的换热系数云图。可见，P/e= 7.93时的换热效果比其他几个肋间距的换热效果好，其通道进口处第一个肋后顶部区域的换热效果优势较明显，而且在出口处换热效果影响区域也最大。P/e=7.93、9和13三种情况中，通道后几个肋间壁面湍流已充分发展，存在高换热区域且都集中在肋后顶端位置；P/e=9和13时肋间壁面的整体换热效果影响区域，比P/e=7.93时的略小，但其整体换热效果明显大于P/e=3和6两种情况。图7示出了不同P/e时带肋壁面的平均努数比。可见，平均努数比随P/e基本呈先增大后减小的趋势，P/e=7.93时的换热效果最好。

由于肋间距不同会影响边界层的分离和再附，适当的肋间距可以为边界层的分离和再附提供足够空间，使得流体在肋片下游再附时产生高换热区域，增强通道整体换热效果。肋间距过小会使得流体在流经下一个肋片时边界层来不及分离，或分离直接冲击下一个肋片，从而影响换热效果的提高。反之，肋间距过大会使得主流在脱离区后来不及进行新的扰动而使热边界层再附并逐渐增厚，边界层增厚造成对流换热热阻增大，同样影响换热效果的提高。

图7 不同肋间距与肋高比带肋壁面的平均努数比Fig.7/Nu0of ribbed surface under different ratio of rib spacing and rib height

图8是不同P/e时通道1/2宽处截面的流线图。可见，当肋间距较小即P/e=3和6时，肋间旋涡结构紧凑、稳定且距离短，边界层来不及分离，旋涡与主流只有靠扩散进行动量和能量交换。P/e=13时，肋后的旋涡不足以覆盖较大的肋间距，分离后的边界层在流动方向有足够的空间再附发展，使得边界层厚度逐渐增加，造成热阻增大，削弱了换热效果。从图6中也可看出，P/e=13时肋间区域靠近肋后顶端的换热最好，沿流向努赛尔数逐渐减小。P/e=7.93和9时，适中的肋间距使得边界层在旋涡扰动后分离与再附，增强了主流与旋涡的掺混，从而提高了换热效果。相比之下，P/e=7.93的整体换热效果最好。

3.2 流阻特性

图9示出了不同P/e下通道的平均阻力系数比。可见，f/f0与P/e整体呈先增后减的趋势。当P/e较小时，旋涡与流体混合较少，压力损失较小；随着P/e的增大，旋涡与主流混合加强，增大了流体的湍流度，进而使压力损失增大；当P/e增大到一定程度后，旋涡作用范围无法覆盖肋间全部区域，这样之后的流动平缓，流动损失减少。此外，一定长度的通道中，肋间距过大使得通道中布置的肋数目减少，同样也减少了流动损失。

图8 不同肋间距与肋高比时通道1/2宽处截面的流线图Fig.8 Streamline of different ratio of rib spacing and rib height at half of the channel width

图9 不同肋间距与肋高比下通道的平均阻力系数比Fig.9 Relationship betweenf/f0and different ratio of rib spacing and rib height

3.3 综合冷却效果分析

引入综合冷却效率η来综合考虑带肋冷却通道的流动损失和换热效果。

对η和P/e通过MATLAB软件拟合，结果如图10所示。可见，在相同边界条件下，在本文优化参数P/e=3～14的取值范围内，η随着P/e的增大先增后减。P/e=5.2时η=0.832为最高，P/e=4～6时η差别不大，P/e＞6后η明显减小。

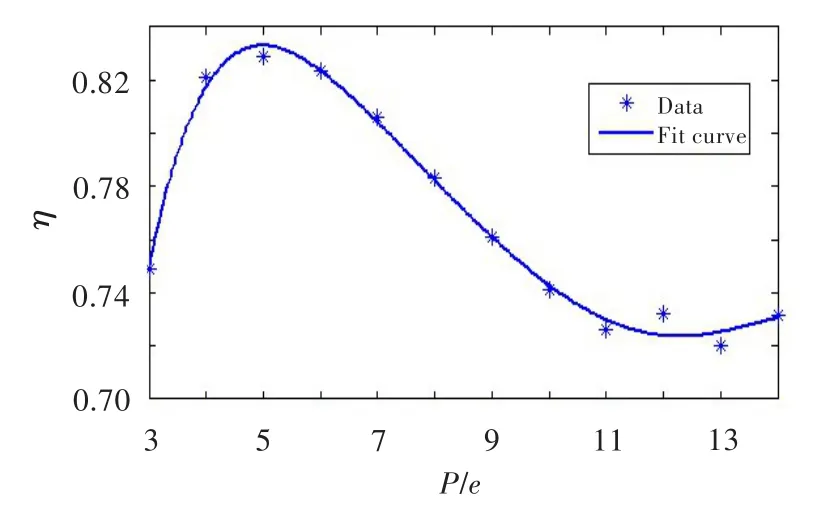
图10 肋间距与肋高比和通道综合冷却效率的关系Fig.10 Relationship betweenηand the ratio of rib spacing and rib height

4 结论

针对内置V型扰流肋直通道的流动与传热特性进行数值模拟，然后对影响流动与传热效果的肋间距与肋高比这一设计参数，运用粒子群优化算法全局寻优，得出如下结论：

(1)当雷诺数为20 000时，通道的整体换热能力和综合冷却效率，均随肋间距与肋高比的增大而先增大后减小，两者都与肋间距和肋高比这一几何参数呈近似函数关系，合理布置肋片位置可提高通道的整体换热和综合冷却效率。

(2)肋间距过小会使得旋涡与主流掺混较少，换热效果和流动损失相对较小；肋间距过大会使得旋涡与主流分离后，主流得不到新的扰动，换热和压力损失下降；肋间距适中会使得边界层在旋涡扰动后分离与再附，增强主流与旋涡的掺混，从而提高换热效果，但同时流体湍流度增大也会导致流动损失增加。

(3)以肋片肋间距与肋高比为优化目标，其取值范围为3～14时，肋间距与肋高比为7.93时具有最好的整体传热性能，为5.2时综合冷却效率最大。

[1]Han J C，Duffa S，Ekkad S V.Gas turbine heat transfer and cooling technology[M].New York：Taylor＆Francis，2000.

[2]Han J C，Park J S．Developing heat transfer in rectangu⁃lar channels with rib turbulators[J].International Journal of Heat and Mass Transfer，1988，31(1)：183—195.

[3]Han J C，Zhang Y M，Lee C P.Augmented heat transfer in square channels with parallel,crossed,and V-shaped an⁃gled ribs[J].ASME Journal of Turbomachinery，1991，113：590—596.

[4]Han J C，Zhang Y M，Lee C P.Influence of surface heat flux ratio on heat transfer augmentation in square channels withparallel,crossed,andV-shapedangledribs[J]. ASME Journal of Turbomachinery，1992，114：872—880.

[5]Ekkad S V，Han J C．Detailed heat transfer distributions in two-pass square channels with rib turbulators[J].Inter⁃national Journal of Heat Mass Transfer，1997，40(11)：2525—2537.

[6]Wright L M，Fu W L，Han J C．Thermal performance of angled,V-shaped,and W-shaped rib turbulators in rotat⁃ing rectangular cooling channels(AR=4:1)[J].ASME Jour⁃nal of Turbomachinery，2004，126：604—614.

[7]Rallabandi A P，Yang H，Han J C．Heat transfer and pres⁃sure drop correlations for square channels with 45 deg ribs at high Reynolds numbers[J].ASME Journal of Heat Trans⁃fer，2009，131：071703-1-10.

[8]Huh M，Liu Y H，Han J C，et al.Rib-spacing effect on heat transfer in rectangular channels at high rotation num⁃bers[J].ASME Journal of Thermophysics and Heat Trans⁃fer，2009，23(2)：294—304.

[9]Liu Y H，Wright L M，Fu W L，et al.Rib spacing effect on heat transfer in rotating two-pass ribbed channel(AR=1:2) [J].ASME Journal of Thermophysics and Heat Transfer，2007，21(3)：582—595.

[10]张勃，吉洪湖，张靖周.肋的几何参数对网格式肋化通道的传热与总压损失特性的影响[J].航空动力学报，2004，19(2)：206—212.

[11]杨阳.弯折化通道流动传热的数值和实验研究[D].南京：南京航空与航天大学，2011.

Numerical simulation on flow and heat transfer in rectangular channel with V-shaped ribs

ZHANG Ai-ping，BI Shuai，FU Lei，CHEN De，LU He，SHEN Zhong-liang
(School of Energy and Power Engineering，Northeast Dianli University，Jilin 132012，China)

A finite volume method with hexahedral structured-meshes and k-ε turbulence model was used to solve the three dimensional compressible Navier-Stokes equations.Numerical simulation was conducted to investigate flow and heat transfer properties in rectangular channel with different ratios of rib spacing and rib height(P/e)of V-shaped disturbed flow rib at inlet Reynolds number of 20 000.The effects of different P/e of v-shaped disturbed flow rib to the heat transfer and flow loss was analyzed,and then the global opti⁃mization to P/e was made.The numerical results show that the overall effect of heat transfer and integrated cooling efficiency of straight cooling channels with ribs are approximated functions with P/e.As the P/e is 7.93,the overall effect of heat transfer of the channel is best;the channel integrated cooling efficiency is op⁃timal when the diversion angle is 5.2.

gas turbine；turbine blade；cooling；rib turbulator；ratio of rib spacing and rib height；overall optimization

TK47

A

1672-2620(2015)01-0025-05

2014-05-07；

2014-07-18

张艾萍(1968-)，男，吉林省吉林市人，教授，博士，主要从事热力设备经济性分析、换热设备传热强化及防/除垢对策研究。