密度泛函理论的基本计算方法研究进展
唐楠楠,张 姝,李强林
(1.成都纺织高等专科学校,四川成都611731;2.四川师范大学化学与材料科学学院,四川成都610068)
0 引言
量子力学是现代物理学的基石。Heisenberg在1925年首先提出了矩阵力学,即是量子力学的矩阵表达形式。随后,Schrödinger在1926年建立了波动力学,即量子力学的波动方程形式。二者虽然在形式上并不相同,但其实分属量子力学的两种表达形式,Schrödinger通过严格的数学推理证明了二者的等价性。相比矩阵形式,Schrödinger的波动方程形式更易于被化学工作者所接收。1927年,Heitler和London将量子化学波动形式运用到氢分子系统的研究工作中,成功得到了精确描述氢分子系统的波函数解析解,并对氢分子系统的化学键本质做出了量子力学解释,这标志着量子化学的诞生。
量子化学的发展给物理学和化学提供了崭新的理论,对于解释微观世界的物质规律和反应本质起到了决定性的作用。但是人们很快发现,对于氢分子以外的大量体系,都很难精确求得解析解。这主要是由于量子化学虽然在理论上严格的描述了微观世界的运动规律,但是在实际求解多粒子体系时会遇到许多困难,有些求解在当时看来甚至是不可能完成的工作。
基于此,科研人员开始研究如何简化计算,通过对模型和方程的近似处理来得到可靠精度范围内的数值解。主要的研究思路是如何将一个多粒子问题转化为多电子问题,进而再将多电子问题转化为单电子问题,如果能够完成这个步骤,会使多电子Schrödinger方程转化为单电子方程,这样就使求解过程被大大的简化。目前被研究人员广泛使用的是 Hartree-Fock 近似处理方法[1,2]和密度泛函理论(DFT)方法[3,4]。
这些理论和方法构成了第一性原理计算(first-principles calculation)[5]。随着计算机科学的迅猛发展,尤其使得基于DFT的第一性原理得到了广泛重视,成为物理学、化学、生物学和材料学等学科的重要研究方法,被广泛运用于各类原子、分子、团簇、晶体和物质表面等的电子结构计算和反应过程分析中[6-8]。密度泛函理论计算是完全以量子化学从头算(ab initio)作为理论依据的计算方法,为了区别于其它量子化学从头算方法,有时也把基于DFT的计算称为狭义的第一性原理计算。本文阐述了DFT理论的发展历程和理论核心,并对其基本计算原理和发展趋势做出重点分析,希望能对DFT理论的进一步完善提供一定的理论参考。
1 DFT计算方法发展历程和现状
近20年来,DFT计算方法被广泛地应用于物理学、化学、材料科学和生命科学等领域。DFT方法因其计算量相对较小、计算结果合理可靠而被人们广泛接受。DFT方法也是目前计算科学当中的主流方法之一,它在量子力学原理和实际应用之间架起一座桥梁,具有不可替代的意义。
密度泛函理论的实质是将波函数转换为电子密度函数作为研究的基本单元,从而简化运算过程,并且使多电子问题得以转化为单电子问题进行求解。假设电子数目为N,则波函数中总共的变量数为3N,求解极其复杂,而采用密度泛函理论,可以将变量数缩减到3个,即只包含了三个空间变量,这样既可以极大的简化计算过程,又可以确保计算精度。
1.1 Thomas-Fermi模型
Thomas和Fermi在1927年建立了基于均匀电子气模型的Thomas-Fermi模型[9]。均匀电子气模型的出发点是假设电子之间无相互作用且无外力干扰。在此基础上得到电子运动的Schrödinger方程为:

解得:

引入0K下的电子排布规律,可经过推导得到电子密度和单电子总能的表达式,分别为:

则体系的动能密度为:

至此,再引入对电子间的库伦势和外场的描述,可以推到出仅由电子密度函数决定的电子体系的总能表达式。依据变分学概念,我们可以认为此时总能是电子密度函数的泛函。Thomas-Fermi模型第一次引入密度泛函的概念,成为后来DFT的雏形。这个模型的成立是基于理想状态下的均匀电子气假设,虽然大大的简化了计算形式和过程,但并没有考虑电子间的交换作用,没有对动能项进行精确描述,所以这个模型非常粗糙,以此算得的结果在很多体系中并不合理。但这个模型给后来的研究者提供了很好的研究思路,经过多年的努力,研究人员在20世纪60年代基本完善了密度泛函理论的内容,并最终建立起严格意义的密度泛函计算理论。对DFT而言,Hohenberg-Kohn定理和Kohn-Sham方程的提出对本理论的形成和完善起到了关键作用,被誉为DFT的两大基石,现分别作如下介绍。
1.2 Hohenberg-Kohn 定理
Hohenberg-Kohn定理是由 Hohenberg和Kohn在系统的研究Thomas-Fermi模型之后提出的,主要针对了非均匀电子气模型,其定理的核心思想是:体系中的所有物理量都可以通过只包含电子密度的变量来唯一决定,而实现方法是通过变分原理来求得到体系基态。Hohenberg-Kohn定理由两条已被严格证明的子定理构成[10]。
(1)处在外势(除电子相互作用以外的势)的忽略自旋的电子体系,其外势可通过电子密度唯一决定。
(2)对于给定的外势,系统基态能量即能量泛函的最小值。
根据已上定理,假设一个体系受到外势的影响,则此时体系的哈密度量由电子动能,外场中电子的势能和库伦作用组成。这三部分中只有外势是根据不同体系而变化的,当对外势的描述确定之后,系统的哈密顿量也就随之确定,而哈密顿量通过Schrödinger方程确定整个体系的波函数,至此,我们可以看出,电子密度的确能够唯一的描述总波函数以及体系基态。此时可以对体系的能量泛函做出如下的描述:
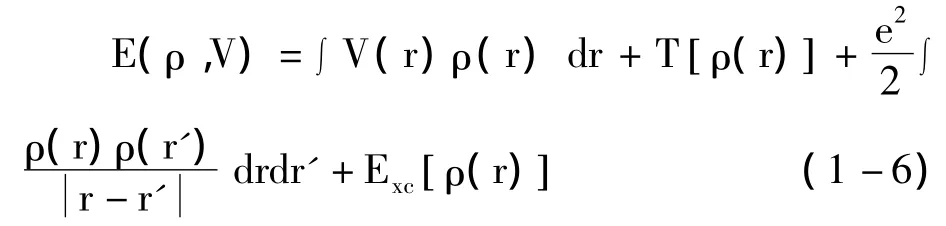
式(1-6)中的四项分别代表外场中的电子势能、动能项、电子间的库伦作用和交换关联能。可以看出,Hohenberg-Kohn定理严格证明了电子密度函数的意义,建立了以电子密度函数为变量的求算形式,并指出了以变分原理为主的求解路径,从这一点看是非常成功的。但是此定理并没有给出求算形式中电子密度函数、动能泛函和交换关联泛函的具体表达式,这使得我们对体系的具体求算还是无法进行。直到1965年,Kohn和沈吕九建立了Kohn-Sham方程[11],得到了各项的具体描述形式,使密度泛函理论开始进入实际应用阶段。其中Kohn因为他在DFT计算方法上的卓越贡献荣获诺贝尔奖。
1.3 Kohn-Sham 方程
依据上文的结论,考虑到体系粒子数守恒,将原方程变分表达式等价为:

Kohn和Sham针对式(1-7)中仍然没有确定具体表达形式的动能泛函项提出使用已经具有明确表达形式的互相无影响的粒子动能泛函来近似代替,而将二者的差异纳入交换关联泛函的未知项中,这样就使得体系仅剩下一个未知量,即新的交换关联泛函项Excρ(r[ ])。定义密度函数:

可将动能泛函项描述为:

将拉格朗日乘子替换为Ei,根据变分原理可得:

式(1-8)、(1-10)、(1-11)合称为 Kohn-Sham方程。通过选取初始电子密度泛函表达式,对体系进行自洽迭代运算得到更为精确的表达式,重复此计算直到满足精度要求,即可以求出体系的近似波函数。Kohn-Sham方程给除了交换关联泛函以外的各项都赋予了明确的表达形式,并把复杂作用项也归并在此项中。至此,求算难度得到大大简化,所有的工作都围绕着如何描述交换关联泛函而展开。
2 交换关联泛函
由上文可知求解问题的关键是建立精确和简洁的交换关联泛函表达式。现对目前常用的方法做出介绍。
2.1 局域密度近似(LDA)
LDA方法也是由Kohn和沈吕九在1965年提出,目的是为了使未知交换关联项能被近似表达,使得DFT能够适用于实际计算。LDA的核心思想是使用已有的均匀电子气密度函数来求算非均匀电子气条件下的交换关联项。假设体系中电子密度随空间的变化率极小,则此时非均匀电子气的交换关联项可以表示为:
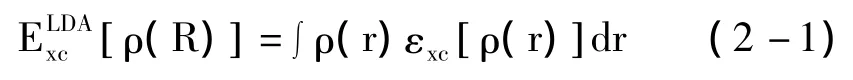
εxc[ρ(r)]表示粒子在均匀电子气中的交换关联能。则相应的交换关联势可表示为:VLxcDA(r)

可得:

式(2-2)和(2-3)被称为Kohn-Sham局域密度泛函方程。通过已上表达式我们不难看出:

式(2-4)说明,交换关联泛函又可以拆解为交换项和关联项两个部分来分别求算。LDA方法求解过程简单,运算成本较低,非常适合电子密度变化率较小的系统,在早期求算一般金属和半导体能带方面发挥了巨大作用。但在实际应用中,许多体系的密度函数变化率都比较大,这使得LDA的在计算物质表面、晶体缺陷等方面误差较大。为了更加精确的计算实际物质体系,人们又创立了广义梯度近似方法。这也是目前密度泛函计算中运用最为广泛的一类处理方法。
2.2 广义梯度近似(GGA)
LDA方法中交换关联项仅仅是电子密度的泛函,这使得在密度梯度变化率较大的体系中容易出现较大的偏差。GGA的近似处理正是在充分考虑到LDA近似算法的不足,将电子密度的梯度也作为交换关联泛函的变量,以此对处在非均匀气体条件下的体系进行能量修正[12]。这就是GGA处理方法的基本思路,具体来看,就是使原项被改写为包含电子密度和梯度函数的泛函形式,若在加上对自旋的描述,即可得到如下的交换关联泛函:

同样的,在GGA当中,交换关联项也可以拆解为交换能和关联能两项分别描述。那么,具体的问题就是如何构建这两部分的合理表达式。关于这个问题,目前主要有两大观点。其一是Beckc等人[13]主张的“一切皆合法”观点。这个流派认为具体的泛函形式原则上可以任意构建,并不需要在泛函中考虑实际的物理意义,那么描述的合理性则完全由实际计算来评价,所以此流派的泛函项通常包含由计算和实验数据统计优化而成的经验参数。在化学相关领域应用较为广泛的GGA-PW91泛函就是根据这个思路构建的。另一类观点则是Perdew等人[14]主张的交换关联泛函应该从实际的物理意义出发,尽量回归到纯粹的量子力学计算理论,所有物理量的计算都仅从电子静质量、普朗克常数、光速等基本常量入手,所以计算泛函表达式也不应过多包含经验参数。在凝聚态物理学等相关领域的计算中经常使用的GGA-PBE泛函即是以这种思想作为构建依据的。
大量的算例证实,GGA通常更加符合实验结果,较LDA适用范围也更加广泛。除了对半导体和某些金属晶格常数优化等少许问题还有待解决外,基本上已经可以算作密度泛函计算中非常成熟的算法,所得结果能够较好的与现有实验参数吻合。
2.3 杂化泛函近似
除了以上两种基本计算形式,研究人员还针对不同体系下的计算需要做出了很多修正LDA和GGA算法。这使得泛函中包含了描述体系的信息越来越多,计算结果也与实际实验数据越来越接近,基本能够以此对体系的实际状态做出客观的衡量。除了LDA和GGA这两种基本泛函形式,还有考虑到Hatree-Fock形式交换作用影响的杂化密度泛函,各类杂化泛函尤其适用于有机化学领域,并在化学反应机理计算方面获得了很大的成功。以文献中经常出现的B3LYP杂化泛函为例:

式(2-6)中涉及到3个参数,并且在求算中用到了B88泛函和LYP泛函分别作为交换项和关联项,即以杂化的方式将Hatree-Fock形式交换作用影响纳入交换关联项中。但需要指出的是,此类杂化泛函算法由于在类自由电子系统的处理上有所不足,因此对金属和窄带隙半导体材料的计算会出现较大的误差,还有待改进[15]。类似的三参数杂化泛函还有 B3PW91、B3P86等等[16],这类泛函采取的思路大致相同,只是选取了不同的参数和泛函种类。
3 展望
近年来随着各种表征技术的迅猛发展,各类电子显微镜和各类电子能谱都已经较成熟地运用于与材料学科相关的各个研究领域。但是传统的研究方法仍然具有诸多不足。例如,使用扫描隧道显微镜(STM)对催化材料进行表面分析时,隧道电流会破坏材料表面的原有结构,同时也可能引起吸附原子的部分脱离,这些都将导致测量结果无法反应材料表面的真实情况。此外,对于在研究反应机理中非常重要的瞬态构象信息,传统的表征手段还不能做到及时捕捉,这使得很多反应机理只能停留在各种理论推测的阶段。另一方面,传统的材料设计主要是通过实验手段来进行,这往往会消耗较长的时间和大量的财力,并且使得实验研究可能出现大量的盲目性。
为了解决这些问题,越来越多的研究者把研究方向转入对材料和反应机理的理论研究,并取得了许多突破性进展。DFT计算方法则是众多理论研究方法中的一个重点,它的进一步发展将会对突破目前材料学科的研究瓶颈起到重要作用。但DFT相比其他方法计算时间较长,同时模型较难运用于分子数较多的体系和含时系统,尤其是目前对于纳米材料计算结果的可靠性也稍逊于模特卡罗方法、分子动力学等方法,这些则是DFT领域发展中亟待解决的主要问题和未来的主要发展方向。
[1]Hartree D R.The wave mechanics of an atom with a non-Coulomb central field [J].Rroc.Camb.Pil.Soc.,1928,24(1):89-110.
[2]Fock V,Petrashen M J.On the numerical solution of generalised equations of the self-consistent field [J].Phys.Z.Sowjetunion,1934,6:368-414.
[3]Hohenberg P,Kohn W.Inhomogeneous electron gas[J].Phys.Rev.,1964,136(3B):B864-B870.
[4]Kohn W,Sham L J.Self-Consistent equations including exchange and correlation effects[J].Phys.Rev.,1965,140(4A):A1133-A1138.
[5]Born M,Oppenheimer J R.Zur quantentheorie der molekeln[J].Ann.Phys.,1927,389(20):457-484.
[6]Van Benthem K,Elsässer C,French R H.Bulk electronic structure of SrTiO3:experiment and theory[J].J.Appl.Phys.,2001,90(12):6156-6164.
[7]Tomohito T,Katsuyuki M,Yuichi I.First-principles study on structures and energetics of intrinsic vacancies in SrTiO3[J].Phys.Rev.B:Condens.Matter,2003,68(20):205213-1-205213-8.
[8]Arques M,Teles L K,Anjos V,et al.Full-relativistic calculations of the SrTiO3carrier effective mass and complex dielectric function [J].Appl.Phys.Lett.,2003,82(18):3074-3076.
[9]Kohn W,Beckc A D,Parr R G.Density functional theory of electronic structure[J].Phys.Rev.,1965,140:B1133-B1138.
[10]Vignale G,Kohn W.Current-dependent exchange-correlation potential for dynamical linear response theory[J].Phys.Rev.Lett.,1996,77(10):2037 ~2040.
[11]李震宇,贺伟,杨金龙.密度泛函理论及其数值方法新进展[J].化学进展,2005 17(2):192-202.
[12]黄美纯.密度泛函理论的若干进展[J].物理学进展,2000,20(3):199-219.
[13]Webster F.Finite-size effects in DFT Calculation of The Phonon-Dispersion In crystalline Silicon[J].Absteracts Of Papers Of The American Chemical Society,1993,206:201 ~inor.
[14]Perdew J P,Burke K,Wang Y.Generalized gradient approximation for the exchange-correlation hole of a many-electron system[J].Phys.Rev.B,1996,54(23):16533-16539.
[15]Paier J,Marsman M,Kresse G.Why does the B3LYP hybrid functional fail for metals?[J].J.Chem.Phy.,2007,127(2):024103-1-024103-10.
[16]Ventura O N.Transition states for hydrogen radical reactions:LiFH as a stringent test case for density functional methods[J].Molecular Physics,1996,89(6):1851-1870.

